基于监测数据的某地铁基坑渗漏风险评估

李卫华, 张生杰, 洪小星, 栾金龙, 谭 勇

(1.南通城市轨道交通有限公司,江苏 南通 226000; 2.同济大学 土木工程学院,上海 200092)

0 引 言

随着我国城市建设和经济的快速发展,越来越多的城市开始进行大规模的地铁建设,城市地铁车站基坑工程不仅面临基坑深度越来越深的问题,而且基坑周边往往建(构)筑物密集,地下管线复杂。如何准确评估基坑安全状态一直是地下工程领域重点关注的问题,国内外许多研究者已经对此进行了大量的研究。

文献[1]提出定量风险评估原则,研究了其在岩土工程中的应用;文献[2]用故障树分析(fault tree analysis,FTA)方法编制某基坑工程边坡开挖的事故树,并用布尔代数法计算了边坡的失效概率;文献[3]采用风险矩阵法对深基坑工程进行风险评估,并对基坑风险管理进行了系统的论述;文献[4]用FTA方法对基坑风险进行评估;文献[5]使用贝叶斯网络综合评估了基坑风险;文献[6]用神经网络的方法对基坑风险进行了预测。这些方法均在基坑风险评估方面取得了很好的效果,然而,这些方法大多是基于各类基坑风险因素对基坑风险进行的整体评估,且评估结果受专家主观评分因素的影响较大,在诸如渗漏等突发事故方面难以进行风险的实时评估。而基坑监测数据则可以较好地实时反映基坑本体及周边环境的状态,尤其是监测数据的累计值和日变化速率对基坑风险评估具有非常好的警示意义,相关工程规范中虽然规定了各项监测数据的警示值,然而这些数据并没有直接体现基坑风险水平,工程所处的风险水平无法得到直观体现[7]。文献[8-9]基于监测数据对基坑风险进行了评估,但是大多数相关研究只是介绍如何在监测数据和风险水平之间建立联系,较少讨论基于实际已经发生事故时的基坑风险评估以及控制措施评估。

因此,本文基于基坑监测数据,利用模糊综合评判方法,围绕某典型在建地铁车站施工过程中出现的渗漏事故进行风险评估,并在堵漏后再次进行风险评估以验证堵漏措施对基坑风险水平的影响。

1 工程案例概况

1.1 工程背景

某滨江城市在建地铁车站为12 m岛式站台地下2层框架结构,位于市区主干道下，且临近两侧建筑群分布密集。车站底板埋深16.75 m,净长180 m,净宽19.3 m。基坑标准段采用明挖顺作法施工,围护结构采用800 mm地下连续墙,竖向设1道混凝土支撑(0.8 m×1.0 m)和3道钢支撑(φ609,壁厚t=16 mm);标准段基坑开挖深度为16.95 m,端头井基坑开挖深度为18.46 m,连续墙深均为39.20 m;基坑安全等级为一级,基坑环境保护等级为二级。

根据场地工程勘察资料可知,工程场地属于长江下游冲击平原,基坑标准段施工范围内地质情况为典型的富水砂层,土体物理力学性质参数见表1所列。

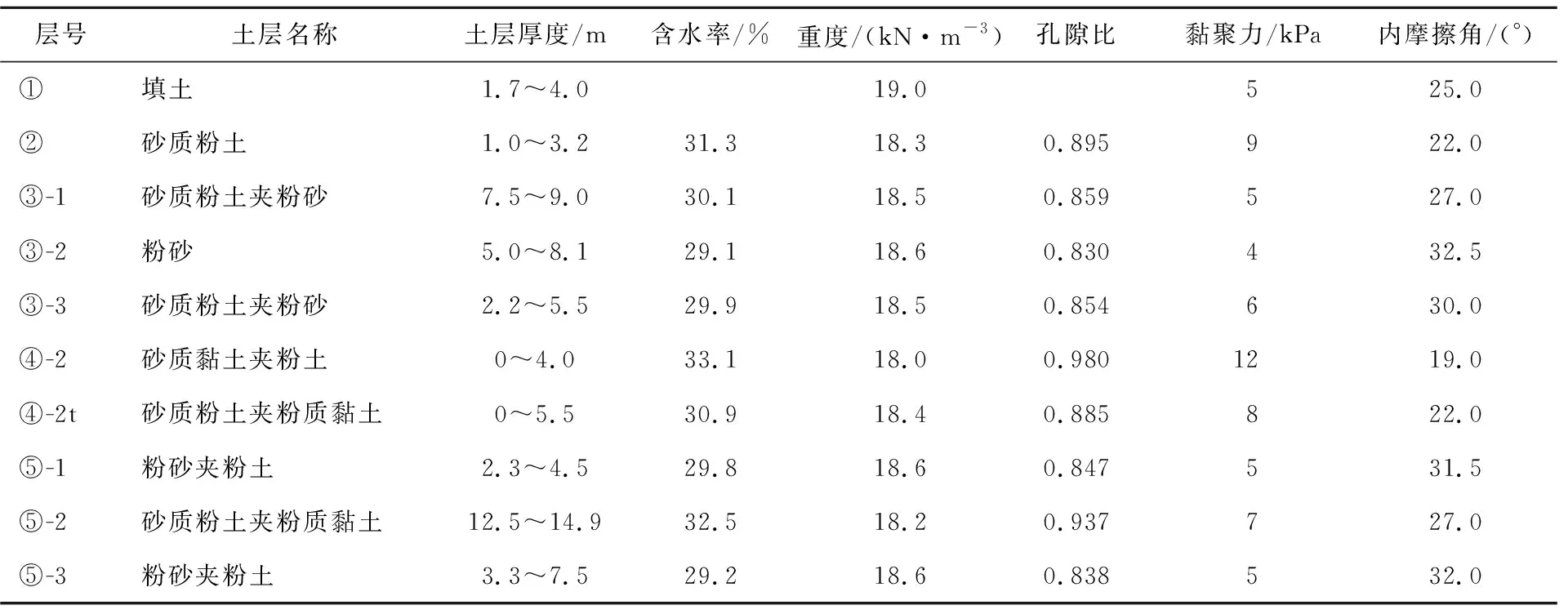
表1 土体物理力学性质参数

潜水主要分布于②～③-3层中;含水层总厚度大,含水量丰富;承压水一般分布在④-2层以下的砂土、粉土层中,承压水的上部隔水层为④-2层砂质黏土夹粉土,其厚度较薄,局部缺失,且该层夹粉土,依据经验场地承压水与潜水存在一定的水力联系。

1.2 事故概况

2019年3月31日,基坑某段开挖深度为11.00 m,第2道钢支撑架设完毕,当日基坑未进行开挖,CX12测斜处附近坑底上方1.00 m左右处出现严重的漏水、涌砂险情。基坑事故发生处位置如图1所示。

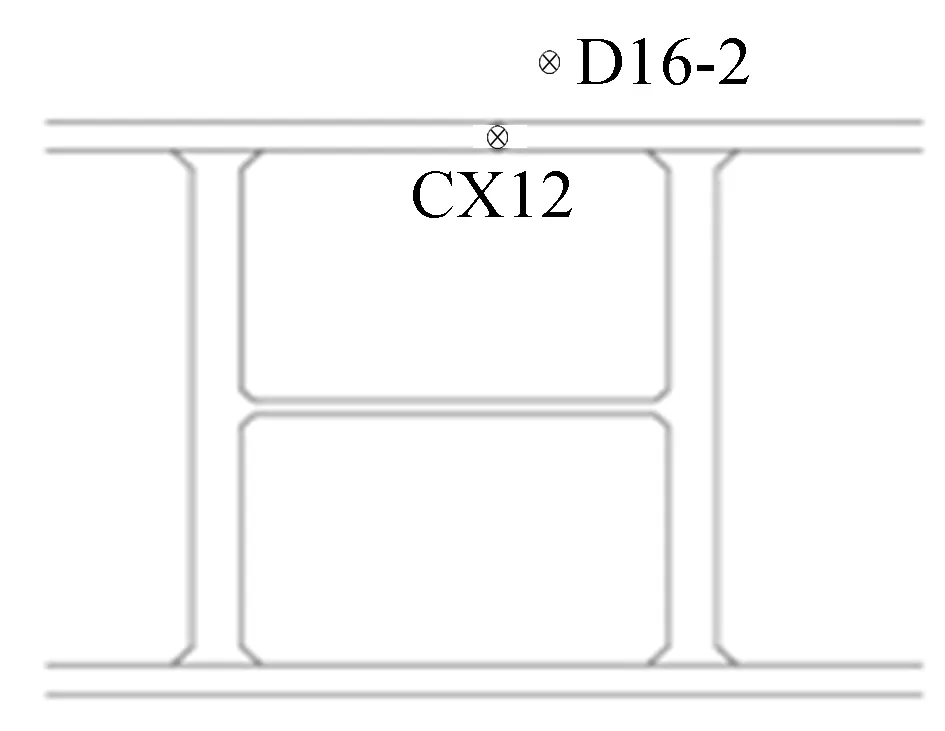
图1 基坑事故发生处位置

根据3月31日的施工监测报表,基坑CX12测斜点变形速率达到10 mm/d,CX12侧附近地表沉降观测点D16-2发生突沉20 mm。

渗漏事故发生后,施工单位立即采取大面积砂袋反压堵漏的措施,由于水土流失严重,险情未得到持续有效的控制,4月2日渗漏处再次发生严重的漏水、涌砂情况,4月3日,施工单位采用坑外注浆堵住漏水源头与砂袋反压结合的方式,有效控制了基坑渗水涌砂的险情,确保了基坑的安全。

险情发生期间基坑CX12测斜处累计变形如图2所示,地表沉降如图3所示(观测时间从3月29日至4月5日共8 d)。

图2 CX12测斜处累计变形 图3 渗漏发生处D16-2地表沉降观测结果

2 基坑风险模糊综合评判

2.1 风险评估因素划分及构造矩阵

根据该基坑工程实际监测的指标和有效数据,将基坑风险评估因素分为4层,如图4所示。第1层为基坑整体;第2层包括基坑本体和周边环境;第3层中,基坑本体包括地下连续墙测斜处变形(简称“地墙测斜”)、支撑轴力、立柱隆沉和地下水位,周边环境包括地表沉降、建筑沉降和管线沉降;第4层为第3层各项的累计值和速率值,其中支撑轴力只有累计值,简称“轴力大小”,水位变化速率简称“水位速率”。

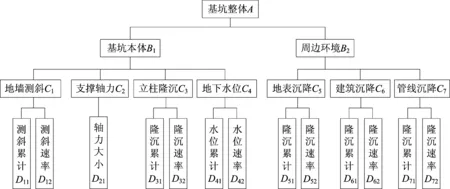
图4 基坑风险评估因素分层

针对基坑风险评估中风险因素多、不确定性强的特点,本文采用模糊综合评判方法。该方法基于层次模型,将评估指标带入隶属函数中进行模糊运算,得到底层隶属度,并结合权重进行逐层加权运算,可得到较全面有效的计算结果,不仅能反映各方面的复杂因素,而且具有定量与定性相结合的特点[10]。

层次模型主要依据九标度法对同级各个风险因子的重要程度进行比较,九标度法中1表示2个评估因素的相对重要程度相同,9表示2个评估因素的相对重要程度差别最大,上述假定即为建立风险评估因素构造矩阵时两两因素判定的依据。本文基于上述理论构造各层风险评估因素的构造矩阵,然后求得各构造矩阵最大特征值,并将其对应的特征向量归一化,即为各风险评估因素的权重[11-12],权重即为各风险评估因素对于基坑安全性的重要程度。基坑风险评估因素第2层为基坑本体和周边环境,其构造矩阵和权重见表2所列,记权重集v2={0.83,0.17}。

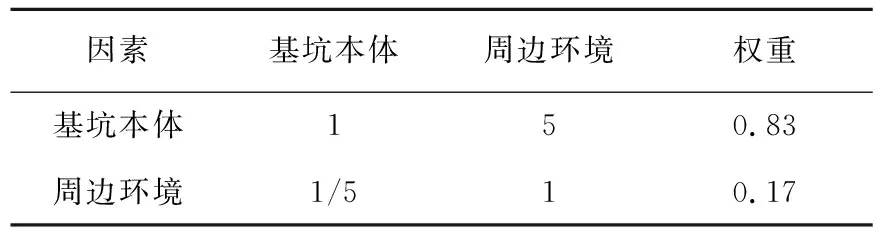
表2 第2层构造矩阵和权重

第3层中涉及因素最多,基坑本体因素集构造矩阵和权重见表3所列,周边环境因素集构造矩阵和权重见表4所列,记权重集v3-1={0.60,0.08,0.20,0.12},v3-2={0.09,0.55,0.36}。

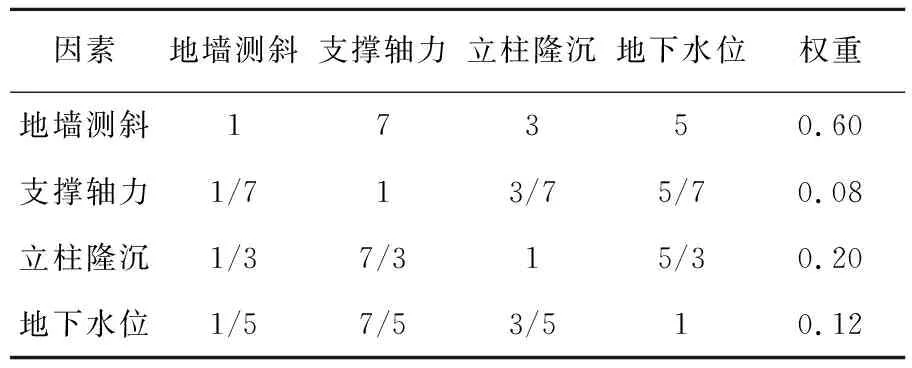
表3 第3层基坑本体构造矩阵和权重

表4 第3层周边环境构造矩阵和权重

除支撑轴力只考虑累计指标外,第4层其他风险因素均考虑了累计变形指标和变形速率指标,虽然2种指标对基坑风险状态的评估均有重要作用,但目前相关研究中大多认为后者比前者更加准确[13],因此在第4层风险因素中累计变形权重取0.30,变形速率权重取0.70,轴力大小权重为1.00,记权重集v4={0.30,0.70}。

为了避免构造矩阵中出现逻辑错误,确保计算结果的整体准确性,需要进行一致性检验。一致性指标(consistency index,CI)取值为(λmax-n)/(n-1),λmax为构造矩阵最大特征值，n为构造矩阵的阶数;平均随机一致性指标(random consistency index,RI)的值见表5所列。

表5 n阶构造矩阵的RI值

一致性比例(consistency ratio,CR)取值为CI与RI的比,以CR值判断构造矩阵的一致性是否可以接受,一般当CR小于等于0.1时,认为构造矩阵的一致性是可以接受的。对于该基坑的计算过程如下:

(1) 第2层构造矩阵。CI为(2-2)/(2-1)=0,CR为0。

(2) 第3层构造矩阵。基坑本体λmax=4,周边环境λmax=3。对于基坑本体,CI为(4-4)/(4-1)=0,CR为0。对于周边环境,CI为(3-3)/(3-1)=0,CR为0。

因此,该基坑的构造矩阵一致性均是可以接受的。

2.2 风险评估分级及隶属函数

在实际施工中,大部分工程很难达到设计监测规程中规定的警戒值要求,在正常安全施工条件下仍然会经常出现报警的情况[14],因此基于基坑工程手册及该基坑工程所在地区的地方监测规程[15-16],结合该基坑工程的设计资料,将基坑风险因素评估指标控制值分为5级:Ⅰ级安全,基坑变形在1.0倍设计允许值内;Ⅱ级关注,基坑变形达到1.0倍左右设计允许值;Ⅲ级预警,基坑变形达到1.5倍左右设计允许值;Ⅳ级报警,基坑变形达到2.0倍设计允许值;Ⅴ级紧急,基坑变形达到2.5倍左右设计允许值。另外,为了便于进行隶属度计算,将地墙测斜、地表沉降等累计变形指标转化相对于开挖深度的无量纲数;支撑轴力指标转化为轴力大小除以设计轴力值的无量纲数;建筑沉降累计变形指标转化为建筑倾斜累计值除以设计允许倾斜值的无量纲数;管线沉降累计变形指标转化为管线沉降大小除以设计允许累计沉降值的无量纲数[17]。基坑各风险因素评估指标见表6所列。

对应5段基坑风险因素指标控制值,将基坑风险等级划分为5个等级:Ⅰ级安全(基坑体系非常安全)、Ⅱ级关注(基坑体系较为安全,但需引起关注)、Ⅲ级预警(基坑体系存在一定隐患,需要召开监测数据分析会议)、Ⅳ级报警(基坑体系存在严重安全隐患,需要召开会议采取一定控制措施)、Ⅴ级紧急(基坑体系极度危险,需要立即进行抢险)。隶属函数为将风险因素评估指标转化为对应各风险等级隶属度的函数,为了便于隶属度的计算,假设表6中各风险因素评估指标的隶属函数相同且均服从线性分布,各风险等级的隶属函数[17]如下:

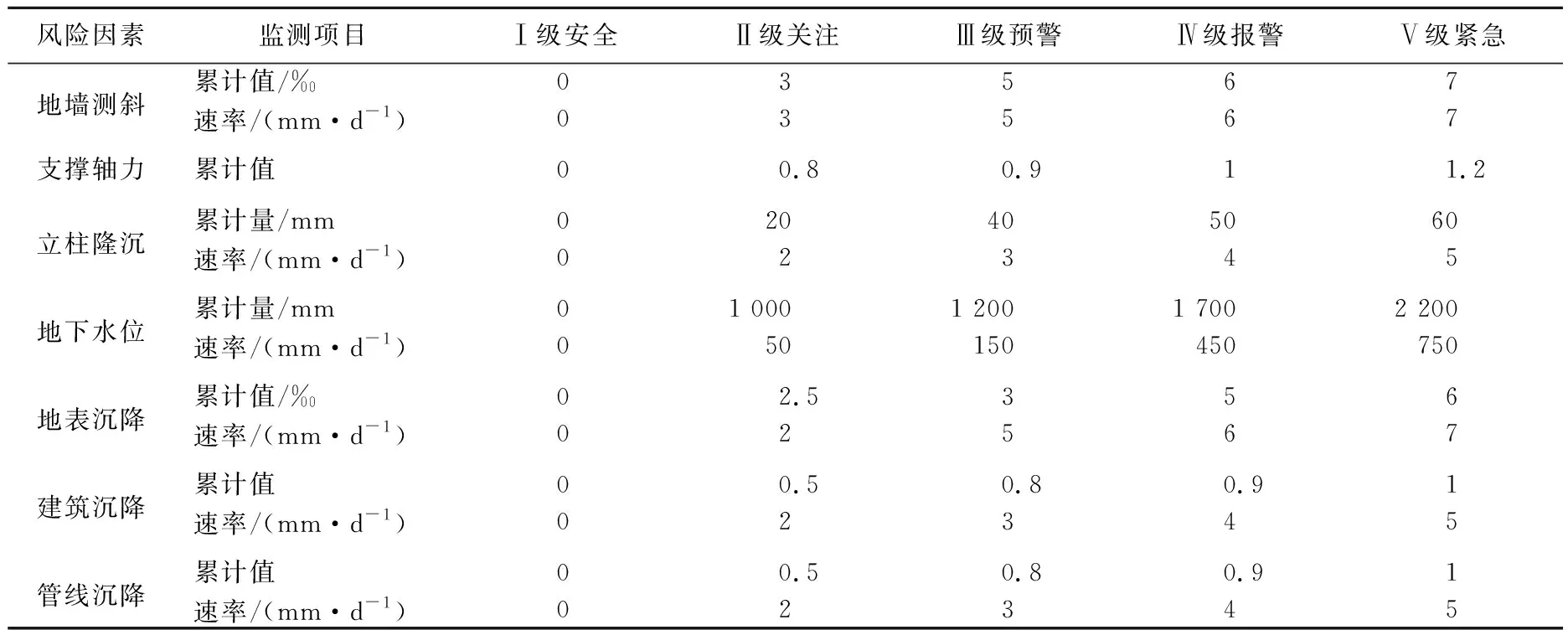
表6 基坑风险因素评估指标控制值

(1) Ⅰ级安全。

(2) Ⅱ级关注。

(3) Ⅲ级预警。

y3=

(4) Ⅳ级报警。

y4=

(5) Ⅴ级紧急。

y1～y5为各风险等级的隶属度;x为各风险因素对应的最大变化量指标,即评估指标;x2、x3、x4、x5分别对应表6中Ⅱ级关注、Ⅲ级预警、Ⅳ级报警、Ⅴ级紧急风险因素的指标控制值。

2.3 基坑风险评估结果

将该工程发生渗漏风险时(2019年3月31日)和采取有效堵漏措施后(2019年4月3日)的监测数据,按照表6的风险因素评估指标进行整理,得到3月31日、4月3日的风险因素评估指标,见表7所列。

将表7数据代入隶属函数中,结合风险因素各层权重集,分别计算该基坑3月31日、4月3日的各层评估矩阵。

(1) 3月31日。第4层评估矩阵如下:

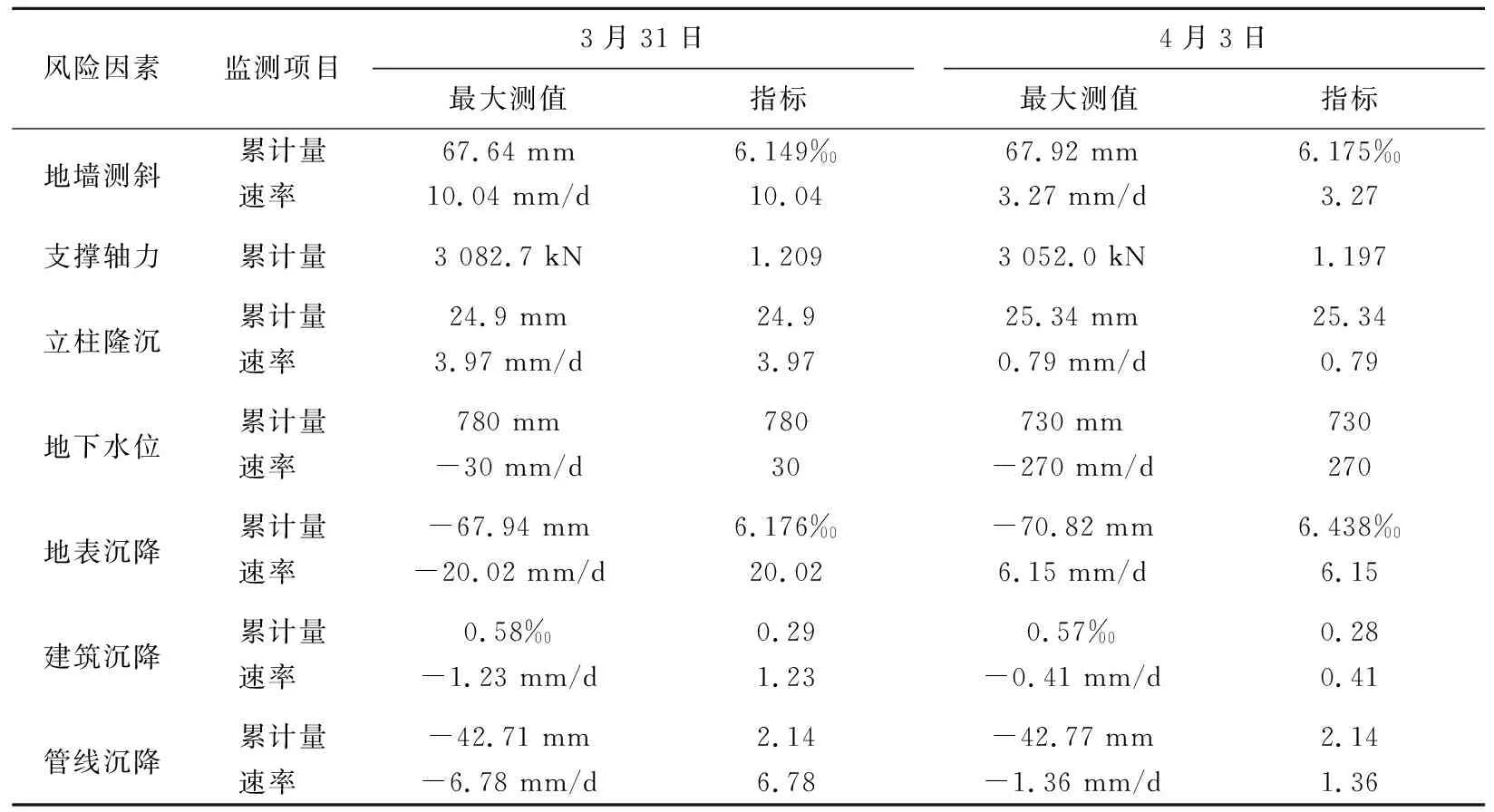
表7 基坑风险因素指标值

第3层评估矩阵如下:

第2层评估矩阵为:

根据最大隶属度原则,3月31日基坑本体以0.67的最大隶属度处于Ⅴ级紧急状态,周边环境以0.55的最大隶属度处于Ⅰ级安全状态。

第1层评估矩阵为:

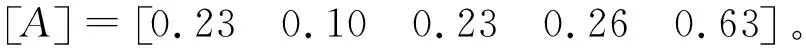
将第1层评估矩阵的隶属度归一化,得到基坑整体的风险概率,见表8所列,基坑工程整体以0.43的最大概率处于Ⅴ级紧急状态,应立即停止施工,召开紧急会议,制定抢险应急方案。

表8 3月31日基坑风险等级概率

(2) 4月3日。第4层评估矩阵如下:

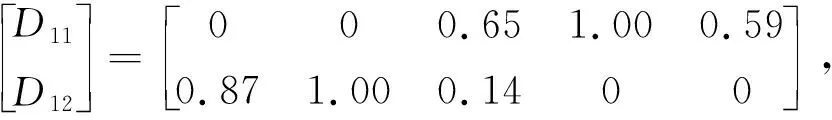
第3层评估矩阵如下:

第2层评估矩阵为:

根据最大隶属度原则,4月3日基坑本体以0.58的最大隶属度处于Ⅰ级安全状态,周边环境以0.80的最大隶属度处于Ⅰ级安全状态。

第1层评估矩阵为:

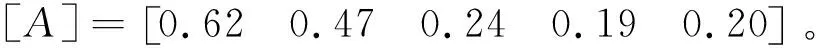
将第1层评估矩阵的隶属度归一化,得到基坑整体的风险概率,见表9所列,基坑工程整体以0.36的最大概率处于Ⅰ级安全状态,抢险措施取得有效成果,基坑渗水漏砂风险得到有效控制,基坑安全稳定。

表9 4月3日基坑风险等级概率

3 结 论

(1) 本文以某地铁基坑工程为实例,基于现场实际监测数据,利用模糊综合评判方法,分别对该基坑工程发生严重渗漏险情时和采取有效抢险措施后的基坑风险状态进行评估,直观反映了基坑的风险状态。

(2) 将基坑工程的风险评估因素划分为4层,基坑风险因素指标计算时充分利用现场监测数据,对部分变化累计值进行转化以利于计算,风险因素指标控制值分级时考虑实际工程现状,区别对待部分苛刻的警戒值要求,基坑风险等级按照5个等级隶属函数进行模糊综合评估。

(3) 3月31日发生地下连续墙渗漏险情时,基坑工程处于Ⅴ级紧急状态,需马上召开紧急会议制定相应的应急抢险方案。在采取砂带反压、坑外注浆等抢险措施后,4月3日基坑工程处于Ⅰ级安全状态,基坑工程渗漏险情得到有效控制,有效保障了基坑的安全。

(4) 工程实例应用结果表明,利用基于监测数据的模糊综合评判法评估基坑风险,具有直观、动态、可靠的特点。