潜在市场规模不确定的以旧换新/再的定价与生产策略
杨爱峰, 董秋雨, 胡小建
(合肥工业大学 管理学院,安徽 合肥 230009)
0 引 言
随着经济和技术的快速发展,产品生命周期越来越短,企业比以往更频繁地推出升级产品以适应激烈的市场竞争,但大量的新品生产所带来的资源消耗和环境污染等一系列问题不可忽视。2013年7月4日,国家发改委等五个部门印发了《再制造产品“以旧换再”试点实施方案》,正式启动再制造产品“以旧换再”试点工作。2019年1月28日,国家发改委会同有关部门印发了《进一步优化供给推动消费平稳增长促进形成强大国内市场的实施方案(2019年)》,为以旧换新消费者提供补贴,支持绿色、智能家电销售,促进产品更新换代。以上政策表明以旧换新和以旧换再受到了政府的高度重视,在此背景下,为了增加消费者的购买需求,实现旧品的再制造、再销售和再循环,企业实施不同形式的以旧换新和以旧换再策略以获得经济效益、社会效益和环境效益。
近年来,诸多学者对以旧换新/再策略进行了深入的研究。文献[1-2]以闭环供应链为研究背景,建立了不同回收主体主导的以旧换新决策模型,研究了各模型下的最优定价与回收策略;文献[3]研究了消费者购买行为和再制造效率对以旧换新策略经济和环境价值的影响;文献[4]假设B2C平台是包括自营商店和第三方商店的双渠道零售模式,B2C平台以购物卡或现金券的形式实施以旧换新,购物卡只能在自营商店使用,现金券是2种商店都能使用,研究了在不考虑或考虑以旧换新努力程度情况下B2C平台的最优以旧换新策略;文献[5]在双寡头竞争环境下,研究了先后进入市场的企业所面临的以旧换新与定价博弈均衡,并分析了竞争存在与否对企业以旧换新策略产生的影响;文献[6]研究了一个垄断的原始设备制造商在第1阶段销售新品、在第2阶段引入以旧换新的两阶段静态和动态定价模型,原始设备制造商对以旧换新回收的旧产品采用2种策略,第1种是不进行再制造仅利用旧产品残值的单市场策略,第2种是再制造并将再制造品销往二级市场或不进行再制造仅利用旧产品残值的双市场策略;文献[7]假设企业针对策略型消费者销售升级换代产品和提供以旧换新,基于消费者的购买行为建立了两阶段动态博弈模型,研究了企业动态定价策略和预告定价策略下的实施条件及对企业利润的影响;文献[8]在消费者短视和以旧换新情形下,企业有一体化与模块化2种产品设计架构策略,同时企业也有静态定价和动态定价2种定价策略,建立了消费者与企业博弈模型,研究了企业的最优产品设计架构和定价策略。
以上文献主要考虑的是以旧换新策略,下列文献主要考虑企业实施以旧换再策略促进再制造品的生产与销售。文献[9]假设新产品和再制造品之间质量无差异,研究了新产品和以旧换再的价格一致、新产品和以旧换再的价格固定但有差异以及新产品的价格固定、以旧换再的价格与使用时间有关的3种定价方式下的最优价格;文献[10]考虑消费者对再制造品的接受程度、新品的耐用性和政府补贴,建立了不提供以旧换再、无政府补贴时提供以旧换再和有政府补贴时提供以旧换再3个决策模型,研究了各模型下产品的最优定价和生产量,并分析了企业提供以旧换再的条件;文献[11]分析了在政府补贴和碳排放机制下新产品和再制造品共存于市场时,再制造品的低价策略或高补贴政策对企业实施以旧换再最优决策的影响;文献[12]根据传统销售和售后渠道以及消费者持有旧件质量的不同细分市场,考虑到消费者的以旧换再偏好程度构建了制造商分级定价利润模型并分段优化,研究了以旧换再补贴下的最优分级定价决策;文献[13]在竞争环境下,针对两阶段闭环供应链系统,研究了古诺竞争型闭环供应链中的以旧换再策略选择问题;文献[14]在以旧换再背景下,针对同时存在原始消费者和新进消费者的情形,研究了制造商的生产与定价策略。
少量文献同时考虑了以旧换新和以旧换再策略。文献[15]在新产品和再制造品共存情形下,研究了企业是否同时实施以旧换新和以旧换再政策,以及以旧换新和以旧换再的最优折扣、碳排放机制、以旧换再补贴的预算约束对最优决策的影响;文献[16]以闭环供应链为背景考虑政府补贴,构建了政府单独提供以旧换新补贴的闭环供应链模型、政府单独提供以旧换再补贴的闭环供应链模型和政府同时提供以旧换新和以旧换再补贴的闭环供应链模型,研究了政府最优补贴决策和企业最优定价策略;文献[17]在碳税政策下,分析了一个同时生产和销售新品和再制造品的制造商为促进再制造品的销售是否应该只提供以旧换再策略,研究了以旧换新和以旧换再策略共存下的最优定价和保修期限;文献[18]将押金与以旧换新/再相结合,假设新顾客在购买新/再产品时需要支付一定的押金,老顾客进行以旧换新/再时可以享受与押金相关的折扣,研究了押金制度下以旧换新/再的产品定价策略。
本文在已有文献的基础上,假设潜在市场规模在第1阶段开始前是不确定的,消费者根据两阶段期望效用决策第1阶段是否愿意购买产品。在第1阶段购买到产品的顾客称为老顾客,在第2阶段决策是否以旧换新或以旧换再(下文简称以旧换新/再)。在第1阶段愿意购买但没有买到产品的顾客称为新顾客,在第2阶段决策是否购买新品或再制造品(下文简称购新/再)。本文构建了以生产商利润最大化为目标,产品价格和生产量为决策变量的两阶段数学规划模型。通过逆向归纳法求解,得出最优产品定价与生产策略,运用解析方法和数值算例对决策变量和目标函数进行了灵敏度分析,并与仅存在新品的基础模型进行了对比。
1 模型假设与符号说明
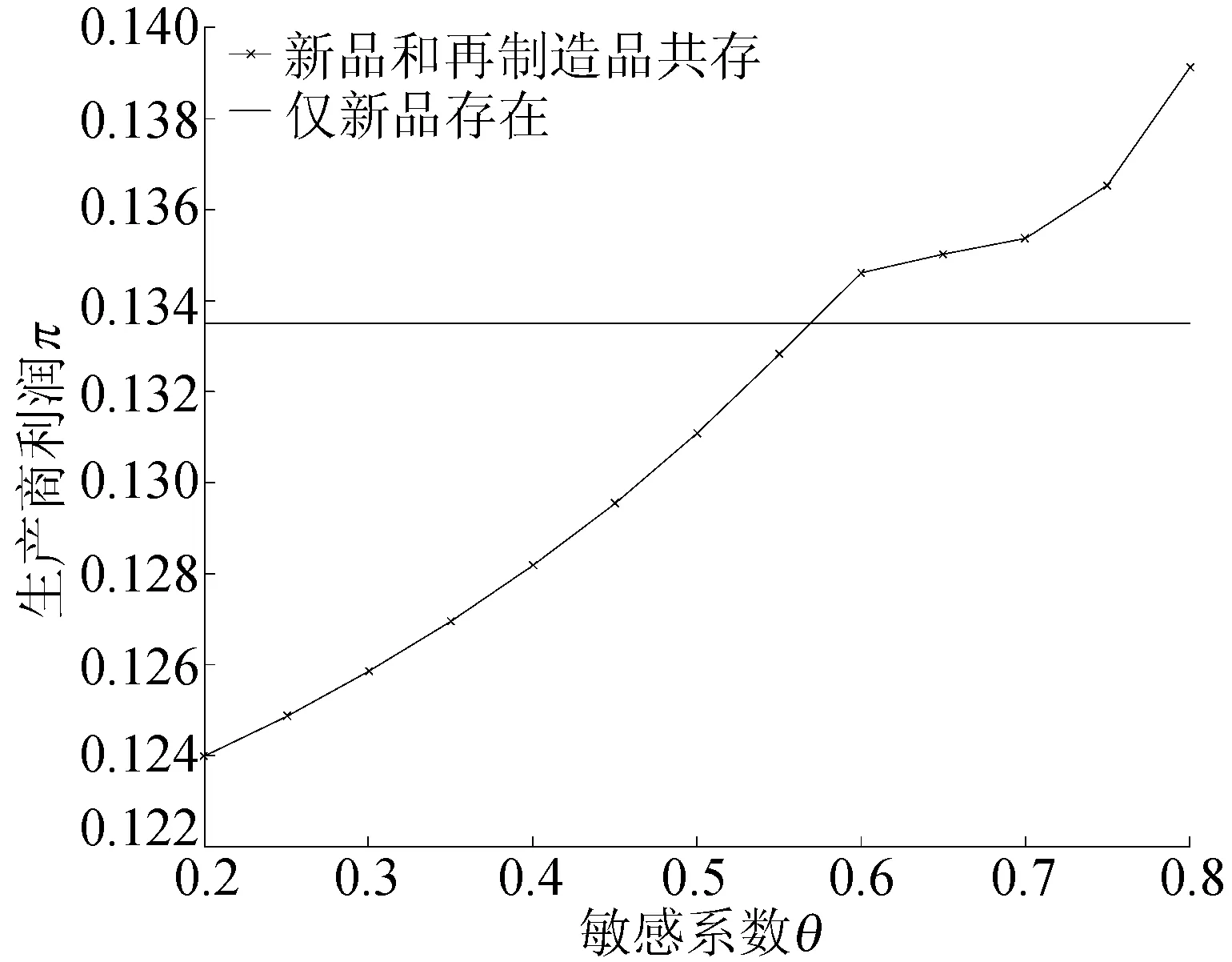
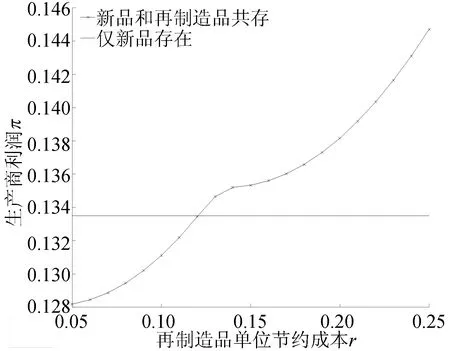
本文假设垄断的生产商在第1阶段销售产品V1,在第2阶段销售其升级产品Vn(新品)和再制造品Vr,Vr为生产商从顾客处回收并进行再制造的产品。若自身回收的旧品不能满足再制造需求,生产商可以外购零件用于再制造,即再制造品的数量不受旧品回收数量的限制。生产商在第1阶段决策产品V1的生产数量Q1和零售价p1,在第2阶段决策升级产品Vn的生产数量Qn、零售价格pbn和以旧换新价格ptn,以及再制造品Vr的生产数量Qr、零售价格pbr和以旧换再价格ptr。产品V1、Vn和Vr的单位生产成本分别为c1、cn和cn-r,其中r(0 潜在市场规模X在第1阶段开始前是不确定的,设其分布函数为F(·),密度函数为f(·)=F′(·)。假设顾客在第1阶段开始前均已到达,顾客对产品V1的估值为v,服从[0,1]上的均匀分布,对升级产品Vn的估值为(1+α)v,对再制造品Vr的估值为(1+θα)v,其中:0<α≤1为升级产品Vn相对于产品V1的创新提升水平;0<θ≤1为顾客对再制造品Vr的敏感系数,θ越小表示顾客对再制造品越敏感。假设顾客对第2阶段产品的价格有理性的预期,顾客会根据两阶段的期望效用来决策第1阶段是否愿意购买产品V1,想要购买产品V1的顾客数量为X1,X1≤X。若X1≤Q1,则每个想要购买的顾客都可以购买到产品,在第1阶段结束时,生产商把剩余的Q1-X1个产品V1以亏本价格s出售,其中s Utn=(1+α)v-ptn-(1-k)v, Utr=(1+θα)v-ptr-(1-k)v。 其中,k为产品V1的折旧系数,k越小表示产品V1越耐用。新顾客在第2阶段有2种选择,购新/再,对应的效用分别为: Ubn=(1+α)v-pbn, Ubr=(1+θα)v-pbr。 生产商以最大化两阶段总利润为目标决策两阶段产品的零售价格和生产数量。根据逆向归纳法,先构建第2阶段的数学规划模型以决策pij和Qj(i=t,b;j=n,r),然后再构建第1阶段的数学规划模型以决策p1和Q1。 首先通过比较效用求出在第2阶段老顾客以旧换新/再以及新顾客购新/再的需求。 需求为Xrqtr。 若用π2表示生产商在第2阶段的利润,则第2阶段的数学规划模型为: π2=Xr[qtn(ptn-cn)+qtr(ptr-cn+r)]+ Xn[qbn(pbn-cn)+qbr(pbr-cn+r)] (1) (1)式的第1项表示生产商从老顾客以旧换新/再业务中获得的利润,第2项表示生产商从新顾客购新/再业务中获得的利润。 引理1 当新品和再制造品共存时,第2阶段产品的零售价pij(i=b,t;j=n,r)和新老顾客的市场规模Xn、Xr无关。 命题1 当新品和再制造品共存时,生产商第2阶段的最优决策为: 证明定义σr=qtn(ptn-cn)+qtr(ptr-cn+r),σn=qbn(pbn-cn)+qbr(pbr-cn+r)。由引理1可知,在π2中决策pij等价于在σr中决策ptj以及在σn中决策pbj(i=b,t;j=n,r)。 首先将qtn、qtr的表达式代入σr中,得σr= 进一步求得其Hessian矩阵为: 推论1表明,当新品和再制造品共存时,以旧换新/再的价格低于购新/再的价格,促进了老顾客重复购买。 推论2表明,随着新品Vn单位生产成本的增加,生产商需要通过提高新品Vn的零售价格来提高利润;随着新品Vn创新提升水平的增加,新品Vn的竞争力将增加,生产商可以通过提高新品Vn的价格来提高利润;随着再制造品Vr的生产节约成本r的增加,再制造品Vr的生产成本越少,制造商将减少再制造品价格,再制造品的优势明显,顾客将由新品转向再制造品,生产商将增加再制造品Vr的生产量和减少新品Vn的生产量;随着顾客对再制造品的敏感系数θ的增加,顾客对再制造品和新品的估值越接近,即顾客对再制造品的接受程度增加,生产商将通过提高再制造品Vr的价格来提高利润;随着产品V1折旧系数k的增加,产品V1越不耐用,老顾客以旧换新/再的需求增加,生产商将通过提高以旧换新/再的价格来提高利润。 (4) 第1阶段购买V1,第2阶段以旧换再,期望效用为μ-p1+E(Utr)=μ-p1+E[(k+θα)× 显然,当且仅当μ-p1+E(Utj)≥E(Ubh)时,即p1-μ+E(Utj)-E(Ubh)(j,h=n,r),顾客在第1阶段才愿意购买产品V1。为最大化两阶段利润,生产商应将产品V1的价格定为消费者的保留价格[3],即p1=min{μ+E(Utj)-E(Ubh)|j,h=n,r),此时第1阶段愿意购买产品V1的顾客需求为X1=X,第2阶段老顾客的市场规模为Xr=X∧Q1,第2阶段新顾客的市场规模为Xn=(X-Q1)+。 若用π表示生产商两阶段的利润,则两阶段的数学规划模型为: (2) 定义z=p1+σr-σn,生产商在第1阶段每销售1个产品V1,除了获得销售收入p1外,增加了1个潜在的老顾客需求,减少了1个新顾客需求,1个老顾客和一个新顾客产生的单位利润分别为σr、σn,因此z表示在第1阶段销售1个产品V1获得的潜在收入。 命题2当新品与再制造品共存时,生产商第1阶段的最优决策为: 证明因为v服从[0,1]上的均匀分布,故μ=E(v)=1/2。 同理可求: 推论3表明,随着单位生产成本c1的增加,由于市场规模在第1阶段开始前是不确定的,生产商会降低产品V1的生产量,以减少滞销损失;随着亏本价格s的增加,产品V1滞销的边际损失减少,产品滞销风险减少使得生产商能够增加产品V1的生产量。 首先求出在第2阶段老顾客以旧换新以及新顾客购买新品的需求。 (3) (3)式的第1项表示生产商从老顾客以旧换新业务中获得的利润,第2项表示生产商从新顾客购买新品业务中获得的利润。 命题3 仅存在新品时,生产商第2阶段的最优决策为: 若用πn表示仅新品存在时生产商两阶段的利润,则两阶段的数学规划模型为: (4) (4)式各项含义与(2)式相同。 命题4 仅存在新品时,生产商第1阶段的最优决策为: 命题4的证明方法同命题2。 下面将新品和再制造品共存情形与仅存在新品情形进行对比。 推论5表明,当顾客对再制造品的敏感系数较大时,即顾客对再制造品和新品的估值差异较小,再制造品进入市场会蚕食新品的销售,然而增加了顾客购买产品的总概率。这是由于再制造品的价格低于新品的价格,并且两者的估值比较接近,因此再制造品一方面吸引了部分原计划购买新品的顾客,另一方面也吸引了部分没有计划购买新品的顾客。 推论6表明,相比于仅存在新品的情况,再制造品的进入扩大了第2阶段的顾客市场,使得生产商将通过低价策略吸引顾客在第1阶段购买产品V1。 当再制造品引入后,销售1个产品V1的潜在收入大于仅存在新品情况下的潜在收入时,生产商将会提高第1阶段产品V1的生产量,尽可能地增加产品V1的销量,从而提高两阶段总利润。 因为潜在市场规模X是不确定的,所以生产商的利润函数比较复杂,很难通过解析方法分析其利润的变化规律。为了便于分析,假设X服从[0,1]上的均匀分布。本节将通过数值算例,分别在新品和再制造品共存与仅存在新品的2种情形下,研究消费者对再制造品的敏感系数θ、再制造品单位节约成本r和创新提升水平α对生产商利润的影响。 参数设定:c1=0.25,cn=0.45,r=0.13,k=0.6,α=0.5,s=0.2,θ在[0.2,0.8]上取值。参数θ对生产商利润的影响如图1所示。 图1 参数θ对生产商利润的影响 由图1可知,消费者对再制造品的敏感系数θ较低时,即再制造品的受欢迎程度较低,再制造品的进入会损害生产商的利润;随着敏感系数θ的增加,顾客对新品和再制造品的估值差异减小,再制造品具有低价的竞争优势,可以吸引更多的消费者购买产品,再制造品带来的利润能够弥补蚕食新品损失的利润,此时再制造品的进入可以提高生产商的利润。 参数设定:c1=0.25,c2=0.45,k=0.6,α=0.5,s=0.2,θ=0.6,r在[0.05,0.25]上取值。参数r对生产商利润的影响如图2所示。 图2 参数r对生产商利润的影响 由图2可知,再制造品单位节约成本r较低时,再制造品相对于新品的成本优势不明显,然而再制造品的零售价相对于新品较低,此时再制造品的进入会损害生产商的利润;随着单位节约成本r的增加,再制造品的成本优势明显,可以吸引更多的顾客购买再制造品,弥补了低价产生的利润损失,此时再制造品的进入可以提高生产商的利润。 参数设定:c1=0.25,c2=0.45,r=0.13,k=0.6,s=0.2,θ=0.6,α在[0.2,0.8]上取值。参数α对生产商利润的影响如图3所示。 图3 参数α对生产商利润的影响 由图3可知,不管再制造品是否存在,随着新品Vn创新提升水平α的增加,顾客对新品的估值增加,生产商可以通过提高价格增加自身的利润。新品创新提升水平α较低时,消费者对新品的估值也较低,生产商从新品获得的收益较低,而再制造品的进入可以促进销售,提高生产商的利润。随着创新提升水平的增加,新品相对于再制造品优势明显,再制造品的进入蚕食新品销售导致的利润损失超过了销售再制造品产生的利润,此时再制造品的进入会降低生产商的利润。 本文假设潜在市场规模在第1阶段开始前是不确定的,生产商在第1阶段开始前公布第1代产品的零售价,在第1阶段开始前公布其升级产品和再制造品的零售价。在第1阶段,顾客对第2阶段产品的价格有理性的预期,将根据两阶段的期望效用之和决策是否愿意购买产品。第1阶段购买到产品的顾客称为老顾客,将根据第2阶段效用决策以旧换新/再;第1阶段愿意购买但没有购买到产品的顾客称为新顾客,将根据第2阶段效用决策购新/再。本文在第2阶段新品和再制造品共存与仅存在新品的2种情形下,建立了以生产商利润最大化为目标,产品价格和生产量为决策变量的两阶段决策模型。本文的主要研究结论如下: (1) 无论生产商是否引入再制造品,以旧换新价格均低于购新价格,以旧换新价格随着折旧系数的增加而增加,新品Vn的最优定价随着其单位生产成本的增加而增加,随着创新提升水平的增加而增加。 (2) 当新品和再制造品共存时,以旧换再价格低于购再价格,以旧换再价格随着折旧系数的增加而增加,再制造品Vr的最优定价随着再制造生产节约成本的增加而增加,随着敏感系数的增加而增加;新品Vn的最优生产量随着再制造生产节约成本的增加而减少,再制造品Vr的最优生产量随着再制造节约成本的增加而增加,产品V1的最优生产量随着其单位生产成本的增加而减少,随着亏本价格的增加而增加。 (3) 当顾客对再制造品的敏感系数较大时,再制造品的引入会蚕食新品的销售,但会增加顾客购买产品的总概率。新品和再制造品共存时第1阶段的最优定价小于仅新品存在时第1阶段的最优定价。当新品和再制造品共存情况下销售1个产品V1的潜在收入较大时,生产商引入再制造品会提高第1阶段的生产量。 (4) 生产商引入再制造品的利润受敏感系数、再制造生产节约成本和新品创新提升水平的影响;当敏感系数较大,再制造生产节约成本较大,新品创新提升水平较小时,引入再制造品可以为生产商带来更多的利润。 进一步的工作可以从以下几个方面进行:① 本文假设是在垄断市场环境下研究企业的产品定价与生产策略,可以进一步考虑在竞争环境下企业的最优决策;② 本文假设再制造品的数量不受限制,但现实中由于回收成本及回收旧产品受限等因素可能导致回收再制造的数量有限,因此可以进一步考虑再制造品数量受限下企业的最优定价与生产策略;③ 本文假设消费者在第1阶段开始前均已到达,但实际上部分潜在消费者可能在第2阶段到达,可以进一步考虑潜在消费者在第2阶段有购买行为时企业的最优决策。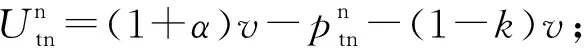
2 新/再产品共存的模型构建与求解
2.1 第2阶段的模型构建与求解
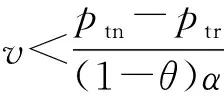
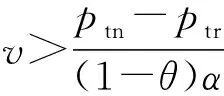
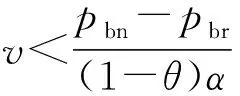
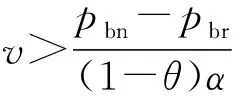
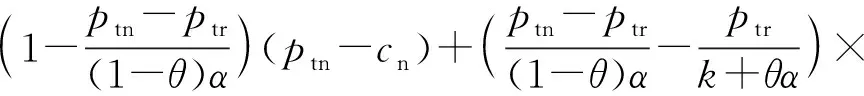
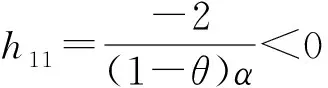
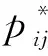
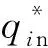
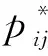
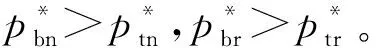
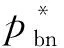
2.2 第1阶段的模型构建与求解
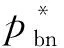
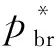
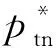
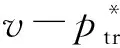
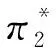
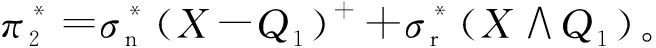
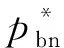
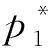

3 仅新品存在的模型构建与求解
3.1 第2阶段的模型构建与求解
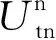
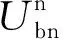
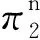
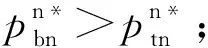
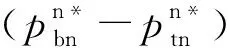
3.2 第1阶段的模型构建与求解
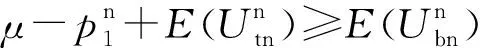
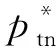
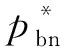
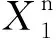
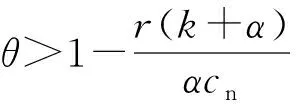

4 数值算例
4.1 参数θ对生产商利润的影响
4.2 参数r对生产商利润的影响
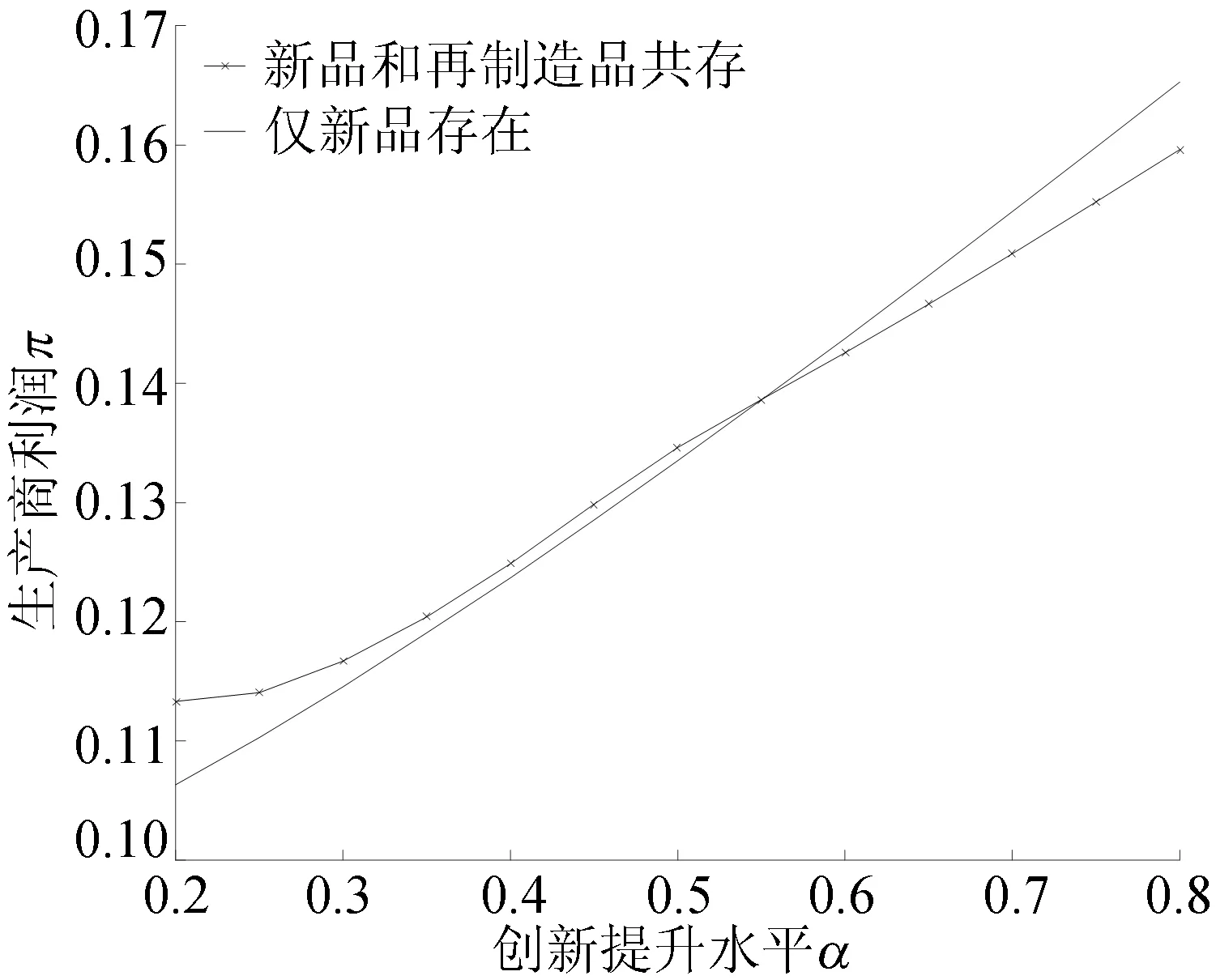
4.3 参数α对生产商利润的影响
5 结 论

