考虑长径比影响的黄土地区钻孔灌注桩桩侧摩阻力取值研究

薛振年，田叶青，董亚琴，周志军

(1.陕西省交通建设集团公司，陕西 西安 710075；2.长安大学 公路学院，陕西 西安 710064；3.陕西交控集团西宝分公司，陕西 西安 710000)

0 引言

黄土沉积覆盖了地球的很大一部分，占世界陆地面积的1/10。黄土在我国很普遍，地层完整，厚度大，面积约63万km2[1-2]。随着我国经济的不断发展，黄土地区的交通发展迅速，大型公路和桥梁的建设也在增加[3-9]。

以往黄土层的桩侧摩阻力取值都是根据其液性指数、土层密实度及桩的类型参考《建筑桩基技术 规范》(JGJ94—2008)来确定，通过本研究的室内模型试验结果分析，桩侧摩阻力取值还与桩长径比有关，且与规范值相比，数值有所差异。在陕西省黄土地区，钻孔灌注桩因其施工技术成熟和承载力高而得到广泛应用[10]。目前，静载荷试验方法是确定桩侧摩擦最广泛使用的技术之一[11-16]。Matte等[17]认为，桩长径比越大，传递到桩端的荷载越小，桩身下部侧摩阻发挥值相应降低，当长径比大于40时，均匀土层中其端阻分担的比例趋于0。朱彦鹏等[18]通过Q2黄土地区3根钢筋混凝土钻孔灌注桩试验研究发现，单桩承载力特征值远大于规范计算值。近年，国内外做了很多桩基静载试验，试验结果表明，实测桩基的承载力与根据规范计算出设计值差别很大，有的偏于不安全，有的设计偏于保守[19]。

因此对于黄土地区的钻孔灌注摩擦桩，其桩侧摩阻力的取值研究至关重要，然而由于桩土之间复杂的相互作用，桩侧摩阻力的确定有一定的难度，胡柏学等[20]对岩溶地区桩基进行静载试验，建立了了软硬化统一荷载传递模型。王非等[21]采用双曲线模型为荷载传递函数提出了用Mindlin解和桩土共同作用的联合方法对荷载传递法进行修正，并计算分析了单桩承载特性。此外，大量室内外试验证明[22-23]，荷载传递函数法可用来求解实际工程的桩侧摩阻力。本研究基于荷载传递法，建立桩的荷载传递模型，并且对此进行理论分析，运用解析法中的双曲线函数求解桩侧摩阻力。双曲线函数中有2个关键参数，经过理论推导与拟合，建立双曲线函数中的关键参数a和b的表达式，进而求解桩侧摩阻力，比较说明计算结果与实测结果的误差，再列举2个工程实例，进一步说明该方法的准确性。

1 模型试验方案

1.1 试验场地及土样概况

本研究模型试验所用的模型箱尺寸为：长2 m，宽1 m，高1.5 m。将模型箱放置在长安大学道路施工技术与装备教育部重点实验室。通过试验得到室内模型试验用土的基本性质指标,如表1所示。

1.2 模型桩的制作

本研究所选取的原型混凝土桩的尺寸为3根半径1.5 m，桩长分别为35，30，25 m的混凝土桩。根据模型几何相似比1/30，3根模型桩MS1, MS2，MS3的半径均为5 cm, 桩长分别为117,1 00, 85 cm。

根据《普通混凝土配合比设计规程》(JGJ55—2011)，设计C30混凝土配合比，浇注3个尺寸为150 mm×150 mm×150 mm的混凝土立方试块，养护后测其强度，28 d的抗压强度为35.7 MPa，可用于模型试验。

1.3 桩身应变片的布置

试验应用的应变片为陕西省某公司生产的BQ120-30AA型号应变片，技术参数为：电阻值(120.4±0.1)Ω，灵敏系数为(2.17±1)%，外形尺寸为36 mm×6 mm。桩身应变片布置图如图1所示。

图1 桩身应变片布置(单位：cm)

1.4 模型试验埋桩过程

埋桩时，回填土的密实度设计为70%，压实填土时，试验结合了电动夯实和人工压实2种方法，电动夯实方法用于压实离桩身较远的周边大范围土体，人工压实桩身附近的土体，尽量不扰动桩身。

1.5 模型试验加载及量测

试验加载采用反力架装置。用小型油压千斤顶进行分级加载，由于桩径较小，千斤顶的量程为10 MPa，该千斤顶的加载范围为0～6 t。桩顶沉降使用2个数显百分表来测定，百分表对称放置，将连接百分表的磁性支座固定在基准梁上。桩身应变数据由DH3816静态应变数据采集系统记录得到。根据《建筑基桩检测技术规范》(JGJ106—2014)要求，选择慢速维持荷载法进行加载，本次试验对每根试桩设计加载10级荷载：MS1试桩的首级加载量为0.5 kN，最大加载量为5 kN；MS2试桩的首级加载量为0.45 kN，最大加载量为4.5 kN；MS3试桩的首级加载量为0.4 kN，最大加载量为4.0 kN。每级加载后1 h内，分别在5，15，30，45，60 min读取桩顶沉降值，若连续出现2次桩顶沉降的差值小于0.1 mm，可以开始加载下一级荷载。本次试验停止加载的条件为：当某级荷载下的桩顶沉降量大于前一级荷载下沉降量的2倍且经过24个h后沉降没有达到相对稳定。加载完成后，进行卸载，每级荷载在卸载时应该持续1 h，在这期间分别于第15，30，60 min时记录百分表的读数，这一级荷载卸载完成；卸载为0后，在前1 h内分别于第15 min和30min测读残余沉降量，之后每隔30 min测读1次，共需持续的时间应不少于3 h。

1.6 试验结果分析

1.6.1 试桩的荷载-沉降特性

3根试桩的最大加载量、极限承载力和对应累计沉降量如表2所示。对MS1，MS2，MS3这3根试桩的荷载-沉降进行对比分析，如图2所示。可以看出，当竖向荷载小于极限荷载时，随着长径比的增大，桩顶沉降量减小；当达到极限荷载以后，随着长径比的增大，桩顶沉降量增大。

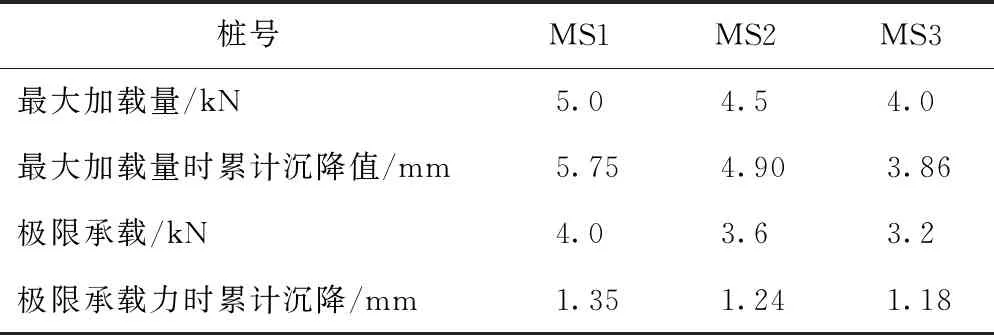
表2 试桩的最大加载量、极限承载力和累计沉降值

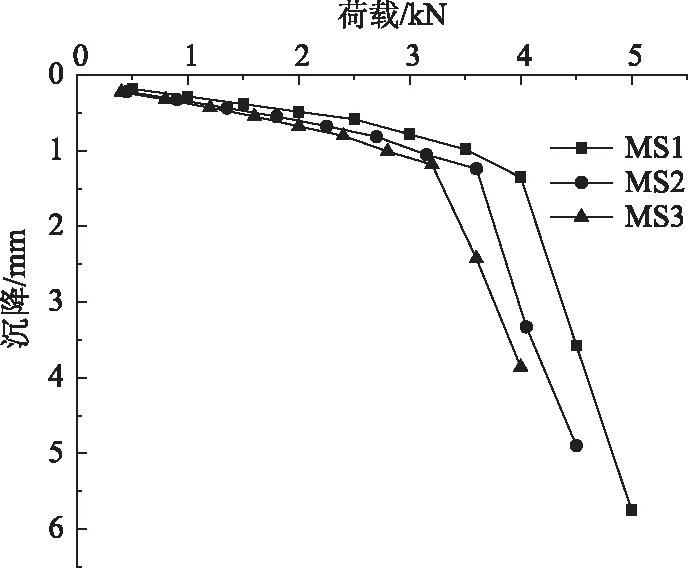
图2 三根试桩荷载-沉降曲线

1.6.2 桩身轴力分析

根据试验数据换算出模型桩的桩身轴力值，绘制出MS1，MS2，MS3试桩的桩身轴力沿深度变化的曲线，如图3所示。

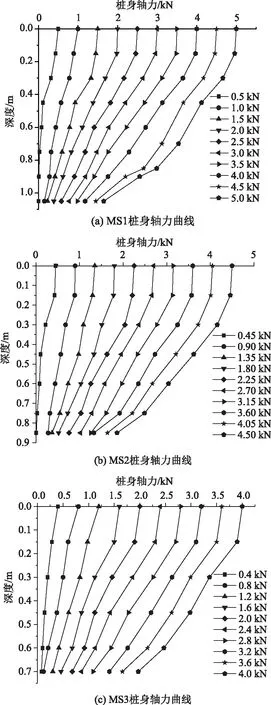
图3 桩身轴力曲线

由图3可以看出，桩身轴力都是沿着深度呈现减小的状态。根据土压力盒所测数据可得，MS1，MS2，MS3在各自极限荷载下的桩底轴力分别为0.88，1.33，1.25 kN，近似将桩底轴力看做桩端阻力，随着长径比的增大，桩端阻力占荷载的比例分别为39%，37%，22%，占比减小，而且可以判断3根试桩为端承摩擦桩。

1.6.3 侧摩阻力分析

根据模型试验计算桩侧摩阻力数值，绘制出MS1，MS2，MS3试桩的桩侧摩阻力曲线，分别如图4～图6所示。

图4 MS1桩侧摩阻力曲线

图5 MS2桩侧摩阻力曲线

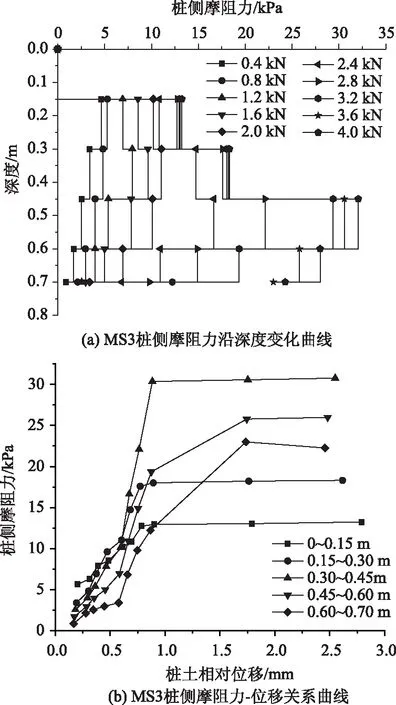
图6 MS3桩侧摩阻力曲线

从图4～图6中可以看出，桩侧摩阻力-位移关系曲线均属于双曲线函数模式。MS1，MS2，MS3试桩达到极限侧摩阻力的位置分别是0.90，0.60，0.45 m处，数值分别是25.66，29.08，32.05 kPa。MS1与MS2相比，极限侧摩阻力减小了13.33%；MS2与MS3相比，极限侧摩阻力减小了10.21%；MS1与MS3相比，极限侧摩阻力减小了24.90%，因此随着桩长径比的增加，桩侧摩阻力达到极限值的位移逐渐下移，并且数值减小。还可以看出，桩身上部的侧摩阻力优先充分发挥作用，随后桩身下部的侧摩阻力开始工作，承担荷载。

1.7 双曲线函数解析法求解桩侧摩阻力

1.7.1 双曲线函数模式

双曲线函数表达式如式(1)所示。

(1)

式中，τ(z)为桩身深度z处的平均桩侧摩阻力；s(z)为桩土相对位移；1/a为起始切线刚度；1/b为桩土相对位移趋于∞时的桩侧摩阻力。

1.7.2 参数a与土工参数的关系推导

在双曲线函数的表达式中，a的表达式为：

(2)

式中，R为桩的半径；χ为系数，取2.5；L为桩入土深度；m为不均匀系数，取1；υ为泊松比；Es0.1-0.2为0.1～0.2 MPa下土的压缩模量。

1.7.3 参数b表达式的拟合

在静力计算法计算β的基础上，1/b的表达式会有一个折减系数，表达式为：

Δ=c1zc2，

(3)

式中，Δ为折减系数；z为桩入土深度；c1和c2为待回归参数。

结合本课题组黄土地区西咸北环线试验区的旋挖钻孔灌注桩资料，该试验区的粉质黏土主要分布层厚为2～15 m和20～40 m，呈现褐黄色、灰黄色，含零星钙质结核及黑色条纹，具有层理特征，基本物理力学性质如表3所示。

表3 粉质黏土基本物理力学性质

结合实测数据，通过拟合曲线(图7)，得出适用于室内试验粉质黏土的双曲线函数中参数b的表达式：

图7 粉质黏土折减系数拟合曲线

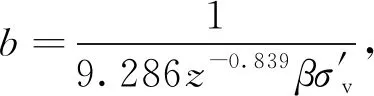
(4)

式中，z为桩入土深度；β为静力计算法中的参数；σ′v为法向应力。

根据参数a和b的推导公式，适用于室内试验粉质黏土的双曲线函数计算表达式为：

τ(z)=

(5)

根据式(5)计算MS1，MS2，MS3在极限荷载下的各深度处的桩侧摩阻力，如表4所示。

表4 在不同深度出处的桩侧摩阻力计算值

对桩侧摩阻力进行加权平均计算，将计算值与实测值进行对比，如表5所示。由表5可知，计算值与实测值的最大误差是18.53%，由于试验中的土体存在很大差异，而计算值都是利用平均值求解得到的，有较大误差属于正常现象。最小误差是7.08%，可以满足工程要求，因此双曲线函数解析法可以用于求解工程中桩基的侧摩阻力。

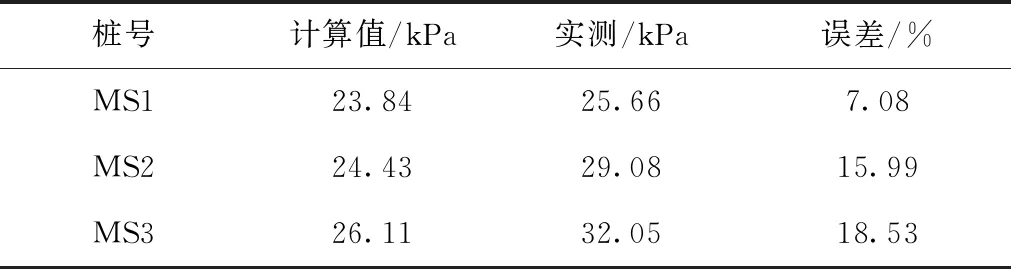
表5 计算值与实测值对比

2 工程实例

2.1 工程实例1

西安市东二环至北二环立交工程桥梁桩基静载试验区旋挖钻孔灌注桩的桩长为18.7 m，桩径为0.8 m，根据资料调研，黄土状土层厚0～15.7 m，黄土状土的基本物理力学性质如表6所示。

表6 黄土状土基本物理力学性质

根据实测数据，桩侧摩阻力的变化规律曲线如图8所示，桩侧摩阻力沿着深度呈现先增大后减小的趋势，桩侧摩阻力-位移关系曲线大致属于双曲线函数模式。

图8 桩侧摩阻力变化规律曲线(实例1)

根据实测数据，用Origin软件拟合出参数b的折减系数的曲线，如图9所示。

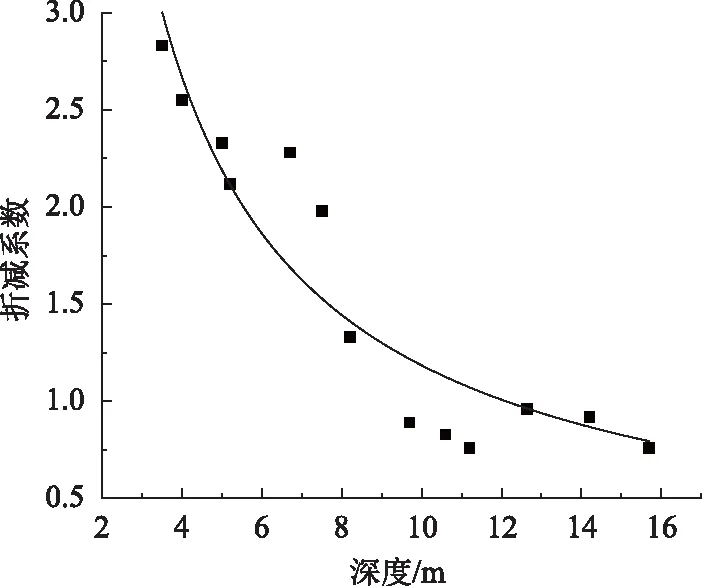
图9 黄土状土层折减系数拟合曲线(实例1)

从图9可知，适用于桩身深度z处黄土状土的参数b的表达式为：

(6)

将参数a和b代入双曲线函数表达式中，计算该试桩极限荷载下的桩侧摩阻。

对各深度处的桩侧摩阻力进行加权平均计算，结果为66.31 kPa，现场实测的极限侧摩阻力为71.39 kPa，计算二者之间的误差：

(7)

2.2 工程实例2

吴定高速公路现场试验旋挖钻孔灌注桩的桩长为25 m，桩径为1.5 m，根据勘察设计的数据表明，试验区的黄土状土层厚0～6.5 m，老黄土状土层厚6.5～50 m。试验区土层的基本物理力学性质指标见表8。根据实测数据，桩侧摩阻力的变化规律曲线见图10，桩侧摩阻力沿着深度呈现先增大后减小的趋势，桩侧摩阻力-位移关系曲线大致属于双曲线函数模式。

图10 桩侧摩阻力变化规律曲线(实例2)

表8 老黄土基本物理力学性质

根据实测数据，绘制拟合曲线，黄土状土层折减系数曲线如图11所示，老黄土层折减系数曲线如图12所示。

图11 黄土状土层折减系数拟合曲线(实例2)

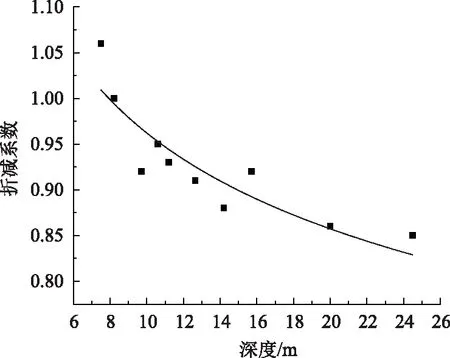
图12 老黄土层折减系数拟合曲线

得出黄土状土层参数b的表达式和老黄土层参数b的表达式：

(8)

(9)

将参数a和b代入双曲线函数表达式中，计算该试桩极限荷载下的桩侧摩阻力。将桩侧摩阻力的加权平均计算值与实测值进行对比，如表9所示。

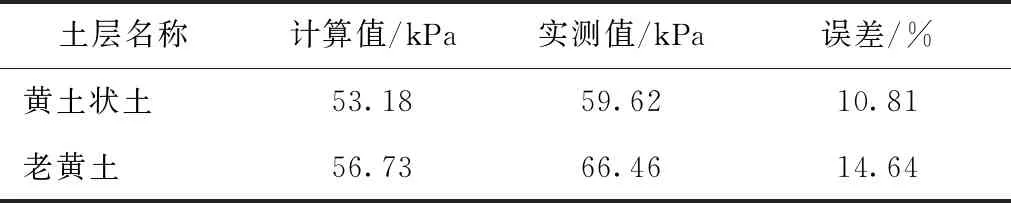
表9 计算值与实测值对比

3 结论

本研究通过室内模型试验，进行了试桩荷载-沉降特性、桩身轴力、桩侧摩阻力分析，运用双曲线函数解析法求解桩侧摩阻力值，通过理论分析，建立了参数a的相关表达式，利用黄土地区工程实例中的大量实测数据，拟合出参数b的表达式，进而计算了室内试验用土的桩侧摩阻力，确定了计算值与试验值之间的误差，最小误差是7.12%，可以将此方法应用于实际工程计算。列举2个工程实例，根据实测数据拟合出不同土层参数b的表达式，将参数a和b代入双曲线函数表达式中计算桩侧摩阻力，计算值与实测值的误差小于15%，进一步验证了该方法的合理性。研究结果可为黄土地区钻孔灌注桩桩侧摩阻力标准值的确定提供参考。