基于改进经验小波变换的桥梁模态参数识别
秦世强,唐 剑,冯嘉诚
(武汉理工大学 土木工程与建筑学院,湖北 武汉 430070)
0 引言
结构模态参数包括频率、阻尼比和模态振型,是结构最基本的动力参数。对桥梁健康监测而言,准确地获取结构模态参数有着重要意义[1]。结构振动产生的信号一般都是非平稳信号,目前处理非平稳信号的方法主要有短时傅里叶变换、经验模态分解(Empirical Mode Decomposition, EMD)、小波变换、经验小波变换(Empirical Wavelet Transform, EWT)等。其中,短时傅里叶变换能分析非平稳信号,但是窗函数一旦选择就固定,这使得短时傅里叶变换时频分辨率受海森堡测不准原理的限制[2];小波变换通过设置不同的尺度因子和平移因子对小波函数进行伸缩和平移,构建出具有不同分辨率的小波滤波器组,从而使小波变换具有多分辨率的特性,因此小波变换可以由粗及细地逐步分析信号,然而,小波变换需要人为设置小波基,因此缺乏自适应性[3];经验模态分解能够自适应地将信号分解为若干个单频率成分的信号分量,结合Hilbert变换可获得信号的时频分布,然而,经验模态分解法存在欠包络、过包络、模态混叠、端点效应、没有严谨的理论背景等问题[4]。经验小波变换是Gilles[5]在2013年提出的一种新的自适应信号处理方法,该方法通过对频谱进行自适应地划分,并建立一组小波滤波器组,对信号进行滤波,将信号分解为一系列具有特定频带的本征模态函数。EWT兼顾小波变换的理论背景和经验模态分解的自适应性,因此在处理平稳和非平稳信号方面具有巨大的优势。目前,EWT已经在机械、电气、土木等领域得到了广泛的应用。向玲等[6]将EWT应用于旋转机械故障诊断,并将EWT与EMD结果进行了对比,结果表明EWT分解得到的故障频率成分多于EMD,且能避免EMD模态混叠、端点效应、计算量大等缺点,为机械故障诊断提供一种新思路。Liu等[7]将经验小波变换应用于地震时频分析,利用该方法对仿真、二维和三维实际数据进行分析,验证了EWT在描述地层特征和构造特征方面优于传统小波变换。陈浩等[8]将EWT结合能量型频率主成分提取方法提出一种脉冲雷达实时加速度估计方法,仿真和理论数据分析结果表明新的方法较之于传统方法精度更高、计算速度更快。赵妙颖等[9]将EWT用于变压器振动信号特征提取,通过计算子分量与原始信号的相关系数,并提取相关度高的分量,该方法能在去除包含较弱特性信息分量的同时达到降低维度的目的,有效减少了计算量。夏雄等[10]利用EWT识别桥梁结构模态参数,通过仿真信号和斜拉桥模型试验测试数据验证了EWT对于信号分解的有效性和模态识别的可行性。
然而,传统的EWT算法存在很多问题,如采用局部极大值、局部极小值的方法进行频谱分割容易受到噪声的干扰,从而影响信号分解结果;对于拥有共振边频带的信号在高幅值边频带位置这两种方法会过多的划分,使得同一个子分量分解到不同的分量中,而低幅值的边频带得不到划分,造成频带划分不合理;而采用尺度空间法分解得到的分量过多,产生了许多虚假的分量,且随着信号复杂度的增长尺度空间法运行时间将会变得很长。针对EWT以上问题,目前的改进方法可以分为4类;(1)更换抗噪能力强的频谱代替傅里叶谱进行频谱分割。刘自然等[11]采用阈值修整后的傅里叶谱包络曲线来确定边界,与传统EWT相比该改进方法更精确地提取与故障相关的信号时频特征,在低信噪比情况下鲁棒性好。Hu Y等[12]提出采用基于顺序统计滤波器的包络方法寻找主要频谱峰值,提出3个准则来筛选有用平顶,以确定EWT所需的边界。万熹等[13]利用burg算法估算出的自回归功率谱代替傅里叶谱进行频谱分割,该频谱对于高噪声或低信噪比的数据有着高分辨率频谱估计。(2)优化边界。Dong S等[14]提出局部窗极大值分割算法确定经验小波变换所需要的频带边界,结合边界优化算法压缩频带带宽,降低分解后子分量噪声水平。(3)筛选感兴趣的分量。Qiao Z等[15]采用尺度空间法确定EWT的边界,利用互信息合并相邻相关分量,故障信号分析结果表明,该方法不仅能有效地减少故障信号的分量,而且能从复杂信号中提取出故障信号成分。郭辉等[16]采用尺度空间法划分频谱,并对峭度值大于阈值的分量作相关性分析,合并相关性高的分量,对合并后的分量进行包络分析,提取故障冲击。(4)对原始信号或者分解后的子分量去噪。李政等[17]提出最大相关峭度解卷积降噪与改进 EWT相结合的滚动轴承早期故障识别方法,试验结果表明新方法能有效降噪、增强信号中周期性冲击特征、实现滚动轴承早期微弱故障的识别。然而对于第1类改进方法同样还是存在许多的不足,例如采用AR功率谱确定边界时AR模型的定阶一直是难题,目前的定阶方法计算出来的阶数并不一定是最佳的模型阶次;确定信号傅里叶包络谱时往往要进行多次包络才能得到最佳包络,最佳包络次数往往是不确定的;采用顺序统计滤波器确定的上包络谱改进时,窗口宽度设定是一个问题,同时有效平顶的选择较为复杂;其他频谱在计算过程中同样存在计算困难,参数设置复杂等问题。为解决上述问题,本研究提出一种改进的EWT(Improved EWT, IEWT);IEWT采用在低信噪比的条件下比傅里叶谱更光滑的EWT趋势谱进行频谱分割,相比于其他频谱,EWT趋势谱构造简单,原理与经验小波变换相同且不涉及其他理论;同时,为消除信号子分量中存在的噪声,进一步引入同步提取变换(Sychroextracting Transform, SET)对分解的信号子分量去噪,提高模态参数识别精度。论文通过仿真信号验证IEWT的频谱划分效果,并以Dowlinghall桥为工程案例,结合随机减量技术(Random Decrement Technique, RDT)与Hilbert变换识别其模态参数,考察IEWT识别模态参数的精度及在不同噪声水平下的鲁棒性。
1 经验小波变换
1.1 频谱划分
EWT通过对频谱进行分割,并建立一组小波滤波器,对信号进行滤波,将信号分解为一系列具有特定频带的本征模态函数,因此,频谱分割是经验小波变换的核心步骤,频谱分割将影响小波分解的精度。首先,对信号进行快速傅里叶变换;然后,将傅里叶谱的频率范围规范化为[0,π],并检测规范化频谱中的所有极大值点以及对应的频率;最后,将所有极大值点进行排序,假设极大值个数为M,经验小波变换分解的模态分量数设为N,此时除了0与π两个边界外,还需要确定N-1个边界,因此存在以下两种情况:
情况1:M≥N,此时该方法搜索到足够多的极大值,保留前N个极大值。
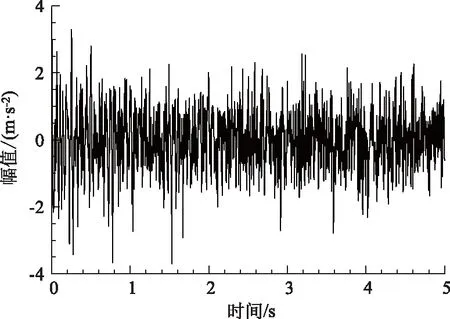
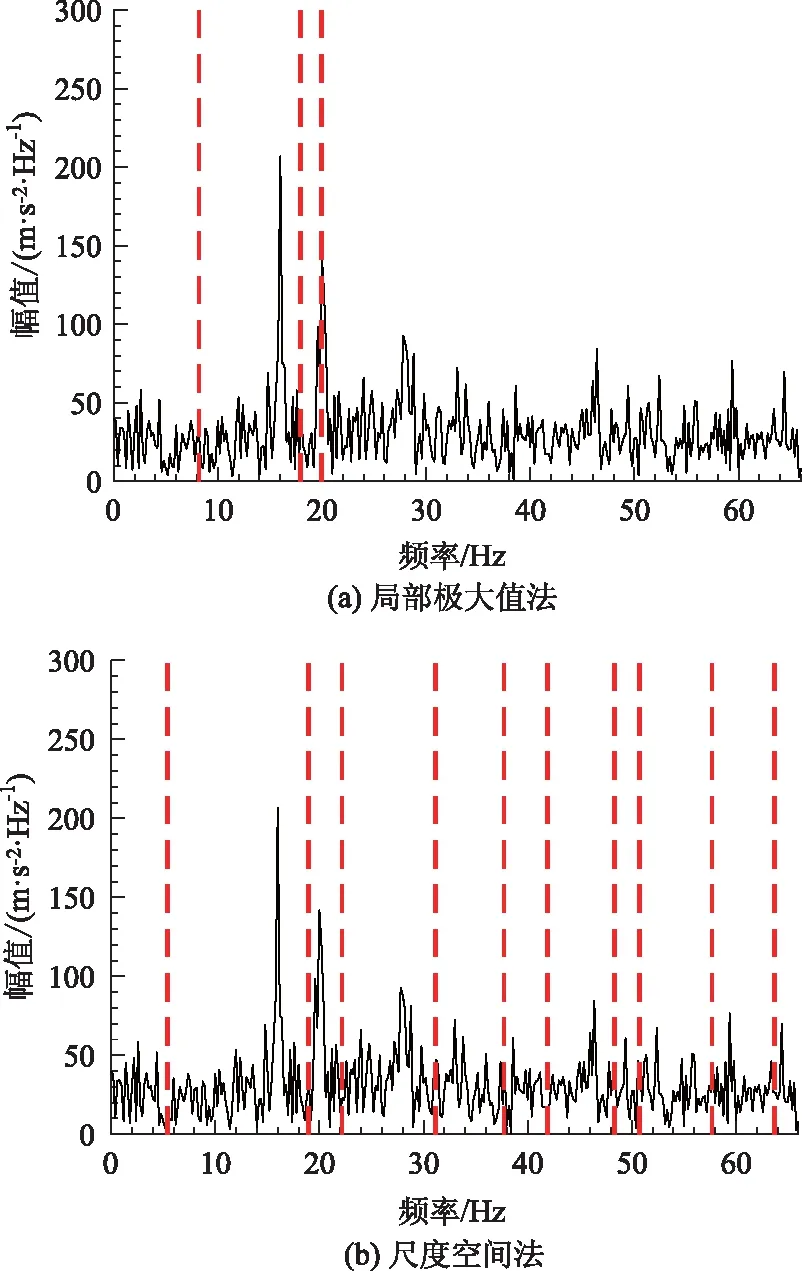
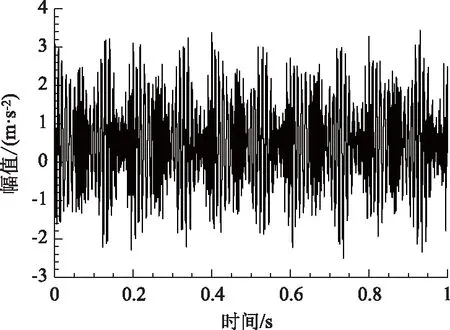
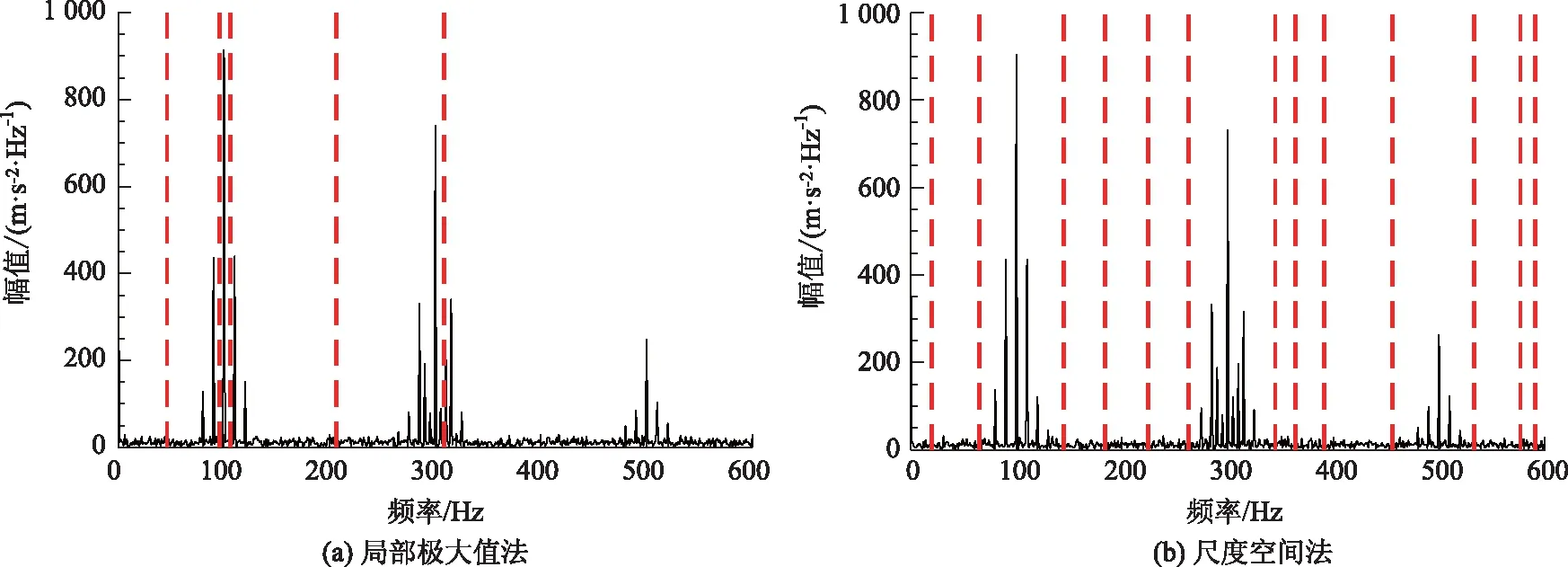
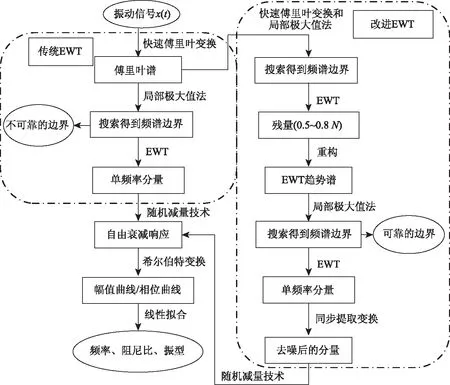
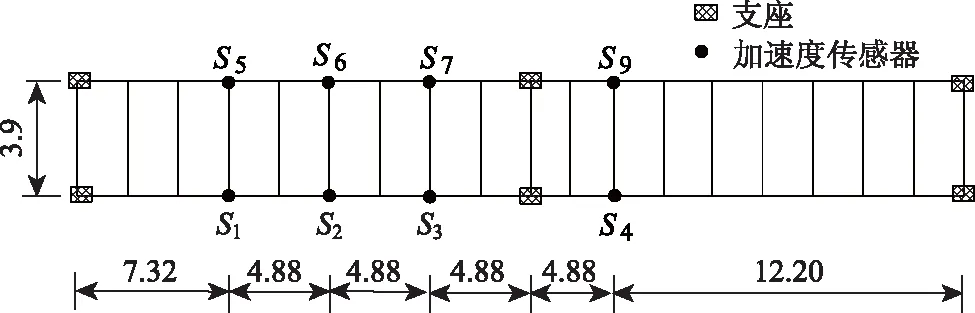
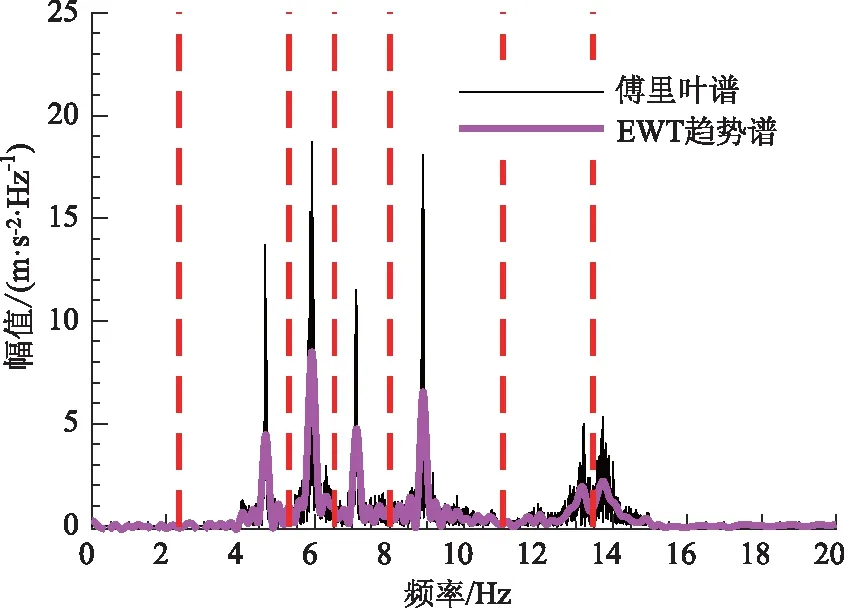
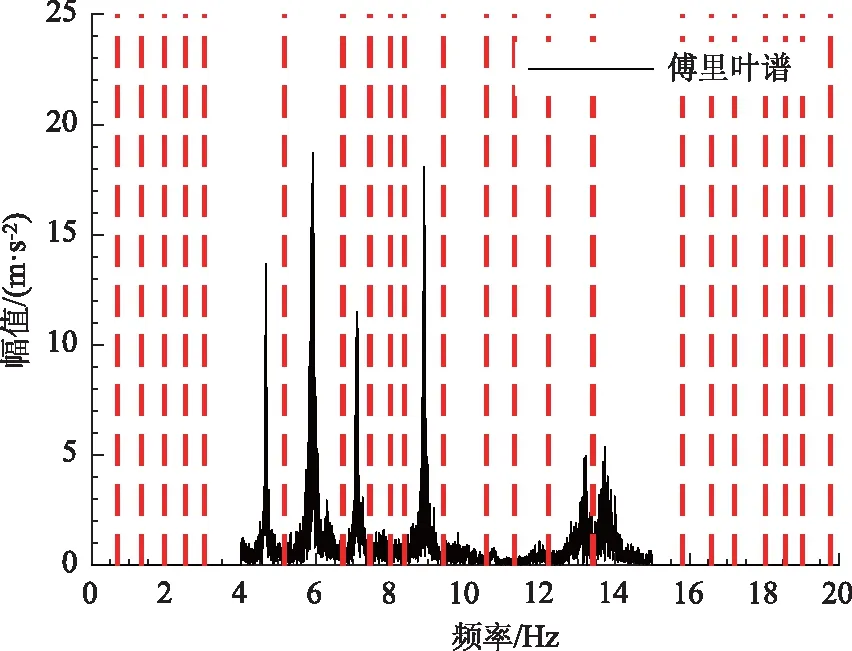
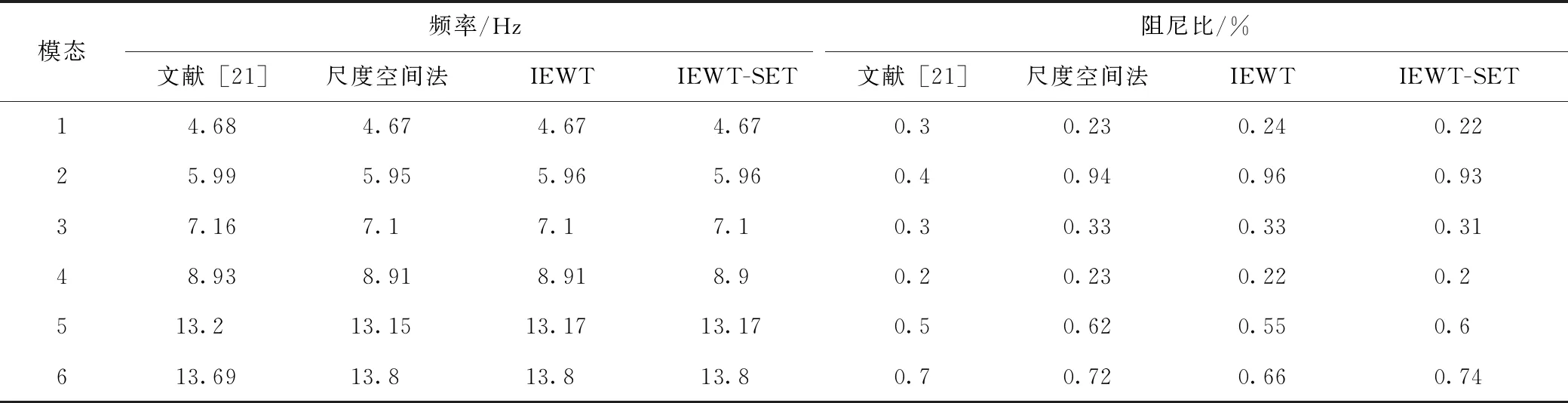
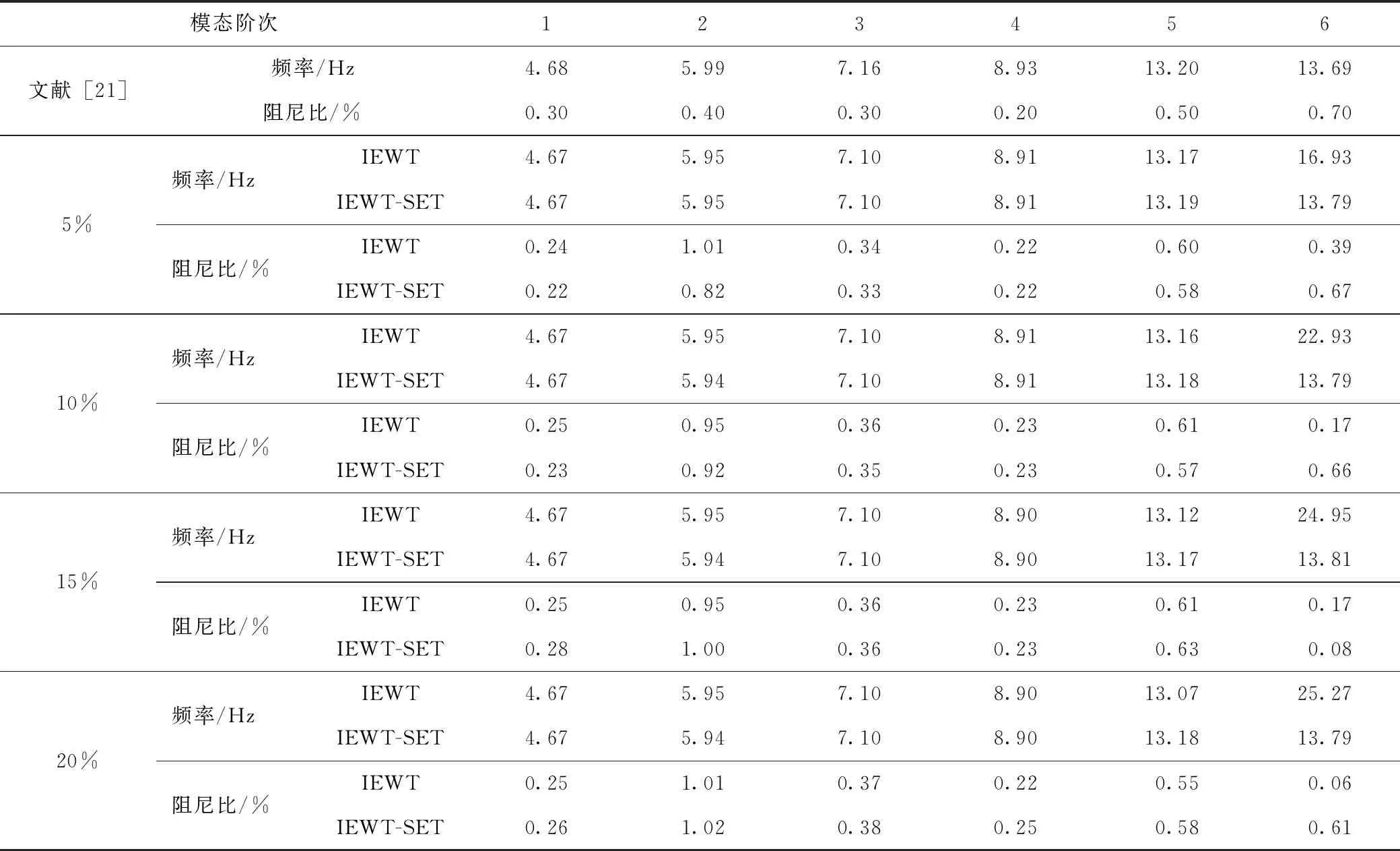
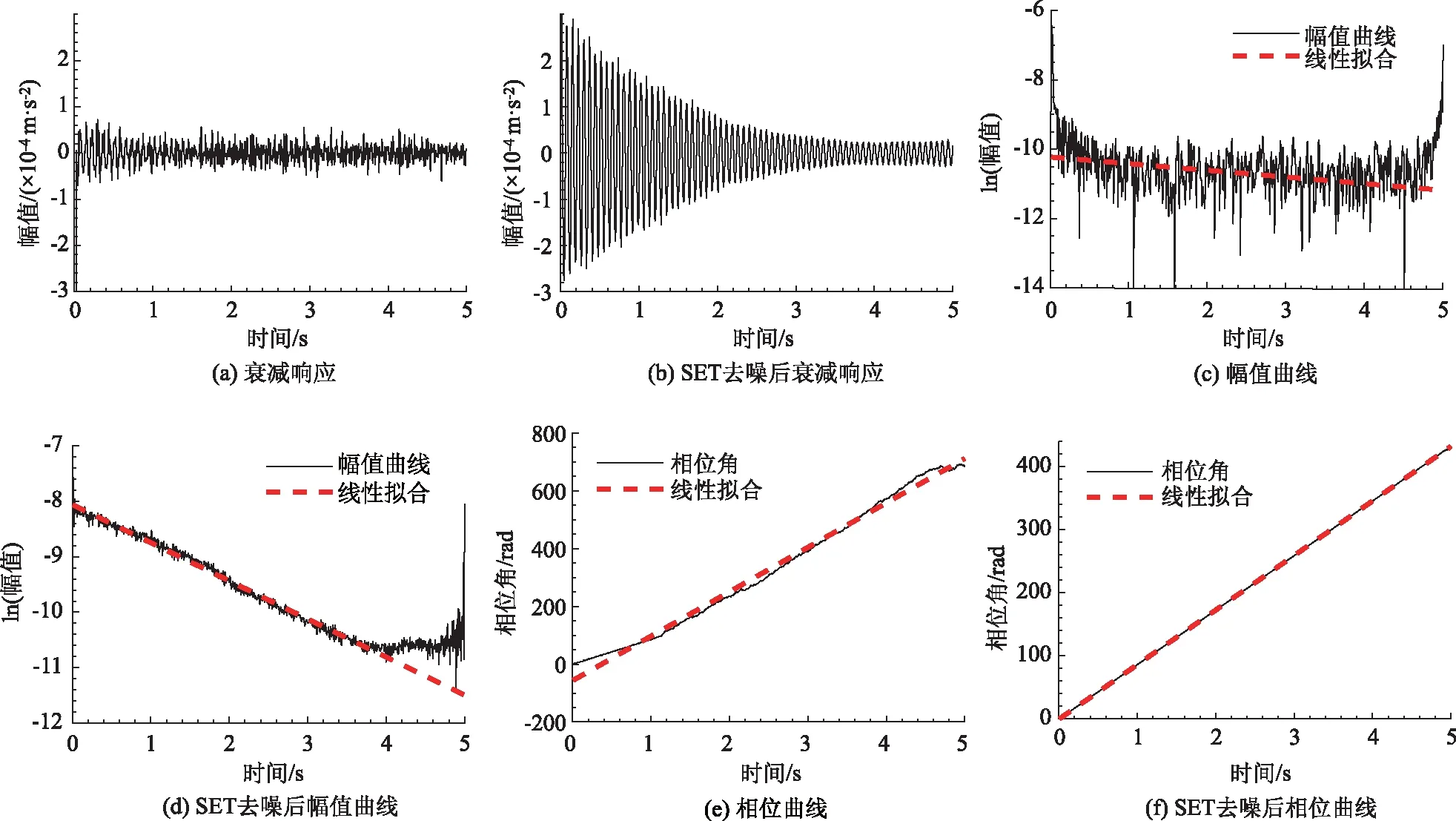
情况2:M 通过对规范化的频谱进行频谱分割,将频率范围为[0,π]的频谱分割为N个连续区间Λn=[ωn-1,ωn](其中n=1,2,…,N且ω0=0,ωN=π)),以ωn为中心,设置带宽为2τn的过渡带,其中τn=γωn,γ为系数。频谱分界如图1所示。 图1 频谱分界示意图 (1) (2) (3) (4) (5) 经验模态fk(t)定义如下: (6) 经验小波变换频谱划分的常用方法一般为局部极大值法、局部极小值法、尺度空间法。局部极大值法、局部极小值法进行频谱分割容易受到噪声的干扰,从而影响信号分解结果。对于拥有共振边频带的信号,在高幅值边频带位置这两种方法会过多地划分,使得同一个子分量分解到不同的分量中,造成频带破裂;低幅值的边频带得不到划分,造成频带划分不合理。ε邻域法需要人工设置初始边界,不具有自适应性,且最终频谱分割结果依赖设置的初始边界,采用局部极大值或者局部极小值设定初始边界时,也存在着两种方法具有的缺陷。尺度空间法得到的边界过多,产生了许多虚假的分量,随着信号长度的增加,尺度空间法运行时间将会变得很长。环境激励下结构的振动受到环境噪声的影响,使得振动信号傅里叶谱存在较多的噪声干扰。同时,快速傅里叶变换算法中补0和截0的措施往往会导致信号失真和频谱泄露等问题,使得振动信号傅里叶谱具有边频带,即除了在固有频率处出现频谱峰值外,与之接近的频率范围内也具有较大的峰值。为了进一步验证经典频谱分割存在的上述问题,通过仿真信号进行数值算例研究。 (1) 仿真信号 由16,20,28 Hz这3种频率分量组成,假定采样频率为240 Hz,连续采样5 s,通过在仿真信号添加高斯白噪声以降低信噪比,使信噪比SNR达到-5.98 dB;该信号的时程曲线如图2所示。 图2 仿真信号s1(t)时域图 (7) 由于仿真信号s1(t)存在3个分量,因此,采用局部极大值法进行频谱分割时,设置的模态分量数N=4。局部极大值法、尺度空间法频谱分割结果分别如图3(a)~(b)所示。从图3(a)可以看出:当在信号中添加了噪声时,傅里叶频谱图在20 Hz左右的位置产生了由噪声分量引起的峰值,其幅值比原信号中28 Hz的分量大;局部极大值法选取的频谱峰值并非是28 Hz的分量产生的峰值,而是噪声分量产生的峰值,因此得到的边界并没有将原信号的3个分量分离开。从图3(b)可以看出:尺度空间法成功分离了原信号的3种频率成分,但同时得到过多的频率边界,后续经验小波变换时,将产生过多的虚假分量。 图3 s1(t)傅里叶谱分割 (2) 仿真信号s2(t)由3个调频-调幅信号组成,其中心频率分别为100,300,500 Hz,调制的频率分别为10,15,20 Hz为了使仿真信号更符合实际,在信号中加入均值为0方差为1的高斯白噪声n(t)。仿真信号s2(t)的时程曲线如图4所示。采样频率为2 000 Hz,采样时间为1 s。 图4 仿真信号s2(t)时域图 (8) 由于仿真信号s2(t)存在3个分量;采用局部极大值法进行频谱分割时设置的模态分量数N=6;局部极大值法、尺度空间法的频谱分割结果分别如图5(a)~(b)所示。由于分量1和分量2的频谱幅值较大,利用局部极大值法进行频谱分割时,检测的边界都集中在分量1和2中,出现了过分解现象;分量3的幅值较小导致在检测局部极值时,即使对含有3个子分量的信号设置分解分量数N=6,分量3频谱幅值峰值点都无法探测到,致使分量2和分量3未得到分离。尺度空间法虽然能将3个分量分离开且3个分量也未出现过分解和混叠的现象,但是在各个分量间划分过多,导致最后分解结果出现虚假的分量,在分析分解后的分量时需要人工选择有用的分量。 图5 s2(t)傅里叶谱分割 针对上述问题,本研究采用趋势谱代替傅里叶谱进行频谱分割,提高频谱分割精度。具体做法如下:(1)对信号的傅里叶谱进行快速傅里叶变换。(2)采用局部极大值法或者局部极小值法分割,分解的分量数设置为N(N>10)。(3)去除分解后的高频分量,用剩余的分量(0.5~0.8N)重构频谱。重构产生的EWT趋势谱与原傅里叶谱具有高度的相似性,与傅里叶谱相比,趋势谱在低信噪比和具有边频带的条件下更光滑,因此,采用趋势谱代替傅里叶谱进行频谱分割能够很好地分解染噪信号和具有边频带的信号。 采用EWT趋势谱s1(t)和s2(t)进行频谱分割,其结果如图6(a)~(b)所示。仿真信号s1(t)的傅里叶谱在20 Hz左右由于噪声的影响产生了毛刺,采用局部极大值法搜索的边界会有偏差,而从图6 (a)看出EWT趋势谱在20 Hz附近很光滑,因此在频谱分割时能很好地将3阶分量分离。具有边频带的信号s2(t)的EWT趋势谱也很光滑,并且不存在边频带,采用局部极大值法探测边界时,仅设置N=4就可以将3个子分量完整分离开来,而利用傅里叶谱结合局部极大值法确定边界设置分量数N=6在分量2和分量3之间仍未探测到边界。 图6 s1(t)和s2(t) EWT趋势谱分割 上述仿真信号的研究结果表明:相较于傅里叶谱,采用EWT趋势谱来确定经验小波变换的边界精度更高,在低信噪比的条件下也表现良好,并且能避免边频带对频谱划分的干扰。 使用EWT趋势谱代替傅里叶谱进行频谱分割,可以减少噪声和其他干扰对频谱分割的影响,但是这种方法并没有去除原始信号中的噪声。信号分解后的各个子分量中仍然存在噪声和部分的混叠,这影响着模态参数识别结果。为此,论文引入同步提取变换[18]进一步处理单分量信号,以降低噪声和混叠对模态参数识别的影响。同步提取变换仅保留时频脊位置的时频系数,其余位置时频系数置0,以达到去除噪声、提高信号信噪比的目的。离散的多分量信号表达式为s(t)=Ae-iω0t,式中,A为幅值;i为虚数单位;ω0为固有频率;对该信号做短时傅里叶变换可获得信号的时频谱G(t,ω),即: (9) T(t,ω)=Ge(t,ω)δ(ω-ω0(t,ω)), (10) (11) 式中,Aj(t),φj(t)分别为第j阶信号分量的幅值函数和相位函数;m为信号的分量数。通过新的时频谱可获得各阶分量的时频脊,进而利用时频脊将原始信号所包含的子分量重建出来。该信号可以重构为: (12) 随机减量技术[20]是一种提取环境激励下结构振动响应自由衰减响应的方法。该方法利用平稳随机响应平均值为0的特性,对原始信号中的确定性分量和随机分量进行辨别,将确定性分量从原始信号中分离出来,得到自由衰减响应。 随机减量技术主要通过选取一个适当的常数A去截取该系统的振动响应信号y(t),可得到一系列不同的交点时刻ti,对以ti时刻后为起点的一系列子振动响应取统计平均值,可得到以常数A为初始振幅的自由衰减振动响应信号x(t)=AD(t),式中D(t)为幅值为1的自由振动响应。 对由随机减量获得的第j阶自由衰减响应进行Hilbert变换,可获得幅值曲线Uj和相位曲线θj(t),即: (13) 式中,Uj为瞬时幅值;ξj为阻尼比;ωnj为固有频率;ωdj为阻尼频率;αj为初始相位。 对希尔伯特变换获得的幅值曲线取对数,可以作出幅值对数曲线,进而拟合幅值对数曲线和相位曲线,并且求拟合直线的斜率,可以计算出第j阶频率ωnj和阻尼比ξj,即: (14) 对于第j阶模态,结构上任意两点p,q振型分量(φjp,φjq)由式(15)决定;其符号由式(16)决定,当相位差为±2mπ时,两者同号;当相位差为±(2m+1)π时,两者异号。 |φjp|/|φjq|=e[Ljp(t)-Ljq(t)], (15) (16) 式中,t0为响应的任意时刻;θjp,q为p,q两点在该时刻的相位差;Ljp(t),Ljq(t)分别为p,q两点幅值对数曲线的拟合直线;θjp(t),θjq(t)为p,q两点相位曲线的拟合直线。以同一点为参考点可以确定该模态其他点的振型分量大小和符号,由此可得第j振型φj。 φj=[φj1,φj2,…,φjn]T。 (17) 以上内容介绍了从桥梁振动响应信号中获取模态参数各个步骤的原理,现将改进经验小波变换、同步提取变换、随机减量技术、希尔伯特变换结合起来,得到基于改进经验小波变换的模态参数识别方法,整个操作流程总结如下: 步骤1:将振动信号x(t)进行快速傅里叶变换获得傅里叶谱。 步骤2:对傅里叶谱进行经验小波变换,采用局部极大值法进行分割,分解分量数为N(N>10),去除高频分量,用前0.5~0.8N项低频子分量进行频谱重构。 步骤3:利用重构的EWT趋势谱,采用局部极大值法进行频谱划分,并建立滤波器组,对振动信号x(t)进行经验小波变换。 步骤4:对各个信号子分量进行同步提取变换去噪。 步骤5:通过随机减量技术对去噪后的分量进行处理,获得自由衰减响应。 步骤6:将自由衰减响应进行希尔伯特变换,得到幅值曲线、相位曲线。 步骤7:采用最小二乘法拟合幅值曲线、相位曲线,得到拟合斜率,利用式(14)~(17),可求得频率、阻尼比、振型。 基于改进EWT的桥梁模态参数识别流程如图7所示。 图7 基于改进EWT的桥梁模态参数识别流程图 Dowling Hall桥[21]是两跨连续钢桁架梁桥,桥面板为钢筋混凝土板。该桥位于美国Tufts大学,全长44 m,宽3.9 m。在2009年4月和6月进行了两组预试验,结果表明环境振动条件下水平振动比垂直测试的振动幅度小得多,且前6阶模态主要集中于2~20 Hz之间,因此在正式试验只收集各测点竖向加速度响应。自2010年1月5日至2010年5月2日,该桥进行了为期17周的持续监测。Dowling Hall桥上共布置了8个加速度传感器,分别为S1,S2, …,S8,各个传感器布置如图8所示。各加速度传感器只测试竖向加速度响应,在本次监测中,采样频率为2 048 Hz,每小时自动采集300 s的数据样本。为了提升计算效率将测量数据从2 048 Hz重采样到128 Hz,选择2010年4月29日15:00时的监测数据进行模态分析。 图8 加速度传感器布置(单位:m) 对各个测点的数据进行[4 Hz,15 Hz]带通滤波去除其中存在的噪声的干扰。然后对滤波后的加速度时程进行分析,以1#测试点为例,滤波后其加速度时程如图9所示。 图9 1#点加速度时程 首先,对获取的EWT趋势谱采用局部极大值法检测边界,并建立小波滤波器组,对加速度响应进行滤波,得到6阶模态对应的加速度分量;其次,采用随机减量技术处理加速度分量,得到各阶模态的自由衰减响应,关于随机减量技术的参数设置,截取的阈值设为信号标准差的1.4倍,衰减长度为5 s。然后,利用希尔伯特变换可以得到各阶自由衰减响应曲线幅值和相位随时间的变化,即瞬时幅值和瞬时频率;最后,分别对幅值对数曲线和相位曲线进行线性拟合,通过式(14)~(17)计算频率、阻尼比和模态振型。EWT趋势谱确定的边界如图10所示。原信号采用尺度空间法频谱分割如图11所示。图12为EWT趋势谱经验小波变换前2阶模态的自由衰减响应、幅值对数、相位图。 图10 趋势谱分割 图11 尺度空间法频谱分割 图12 前两阶模态自由衰减响应、幅值曲线、相位曲线 根据式(14)~(15)可求得频率、阻尼比,其结果如表1所示。各阶振型向量由式(16)~(17)计算得到,用MATLAB拟合各点画出的振型图如图13所示。对比图10和图11可知:EWT趋势谱能够很好地反映出原傅里叶频谱的变化趋势,两者的形状也基本一致,对EWT趋势谱进行N=7的局部极大值法频谱分割,6阶分量很好地分离开来;采用尺度空间法确定原傅里叶谱的边界,虽然也能分离前6阶模态,但是产生了多余的分量,进行模态识别时要事先判断各阶分量是否为有效模态,同时尺度空间法运行的时间太长,在很大程度上降低模态识别的效率。由表1两种方法模态识别结果对比来看,采用IEWT,IEWT-SET(表示用SET对IEWT获得的信号分量进行去噪)、尺度空间法识别出来的模态差别较小,说明了改进方法在高信噪比的条件下有着良好的模态识别能力,识别出来的模态精度较高。在识别过程中改进算法程序运行所需时间也比尺度空间法少且不需要对EWT分解的分量进行人工筛选。 表1 DowlingHall桥模态参数识别结果 图13 Dowling Hall桥前6阶振型 对各个测点的数据添加幅值为振动信号最大幅值5%,10%,15%,20%的噪声以验证改进方法在低信噪比条件下的鲁棒性。对加噪后的加速度响应频谱分割,进行经验小波变换,对子分量作用同步提取变换去噪,结合随机减量技术和Hilbert变换,可识别不同程度噪声条件下的模态参数,其结果如表2所示。 表2 Dowling Hall桥加噪后模态参数识别结果 图14为1#测试点在10%的噪声条件下第6阶模态SET去噪前后自由衰减、幅值对数拟合、相位拟合,很显然去噪前自由衰减响应存在着大量噪声,导致幅值对数图和相位图产生很大的偏差,而将第6阶信号子分量SET去噪后的自由衰减响应曲线线型较为理想,幅值对数图和相位图拟合效果好。由表2可以看出,采用IEWT和IEWT-SET均能准确识别各个噪声条件下前4阶频率,误差较小。主要是因为在EWT分解后前4阶分量虽然存在噪声,但是噪声强度并不大,采用随机减量技术可以消除部分噪声对模态识别的影响,因此前4阶模态识别误差不大。而噪声主要分布在高频区域,随着噪声强度的增加,第5阶模态对应的振动信号分量噪声水平增加,而随机减量技术抵消噪声干扰的能力有限,因此采用IEWT识别的频率误差也逐渐增大。第6阶模态由于频带过宽导致原始信号加入噪声对该模态对应的信号子分量信噪比影响很大,使得在加入5%的噪音时频率的识别结果就产生了较大的偏差,而且随着噪声水平的增加这种偏差也越来越大。而采用IEWT-SET在各种噪声条件下仍然能准确识别第5,6阶模态,即使加入了20%的噪声,频率的识别结果精度仍能保持较高的精度。 图14 第6阶模态去噪前后自由衰减、幅值曲线、相位曲线 本研究针对经验小波变换对于低信噪比和具有边频带信号分解效果较差的缺陷,提出了一种基于EWT趋势谱频谱分割的改进的EWT方法,并结合SET去噪、RDT和Hilbert变换进行桥梁结构的模态参数识别。以两个典型的仿真信号验证采用EWT趋势谱确定EWT边界的可行性和有效性,并将该方法应用于Dowlinghall桥的模态参数识别验证使用所提方法进行模态参数识别的准确性和鲁棒性。可以得出以下结论: (1)EWT趋势谱能准确地确定经验小波变换所需要的边界,即使对于低信噪比和具有边频带的信号也表现良好。 (2)基于该改进方法识别环境振动条件下的结构频率、阻尼比、振型是准确可靠的。该方法能有效地在低信噪比的条件下识别出结构的模态参数,是一种精度高、鲁棒性好的结构模态参数识别技术。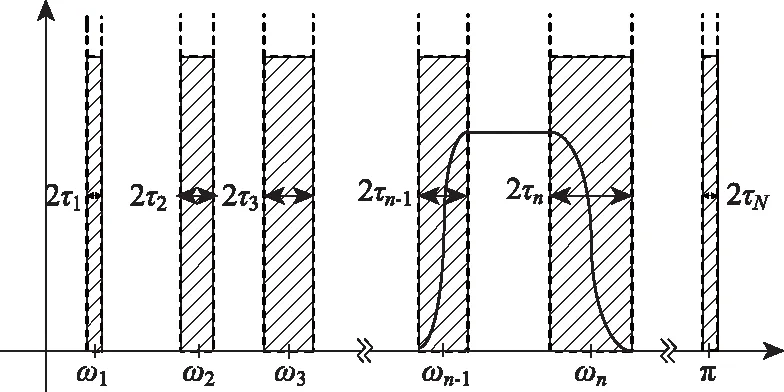
1.2 滤波器的建立
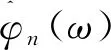
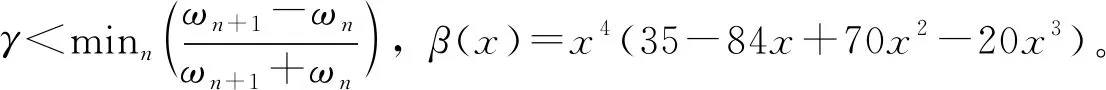
1.3 经验小波变换

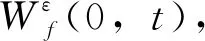
2 改进经验小波变换
2.1 经验小波变换的缺陷
2.2 EWT趋势谱

3 基于改进经验小波变换的桥梁模态识别
3.1 信号子分量去噪

3.2 随机减量技术
3.3 基于Hilbert的模态参数识别
3.4 基于IEWT的桥梁模态参数识别步骤
4 工程案例
4.1 改进方法模态识别精度


4.2 改进方法在低信噪比条件下的鲁棒性
5 结论
——2018年全国高考Ⅲ理科数学21题别解

