桥梁挡风障参数对行车稳定性影响分析
王兆樑,练江峰,詹铠臻,刘功毫,林 立
(1.厦门市公路事业发展中心,福建 厦门 361000;2.厦门中平公路勘察设计院有限公司,福建 厦门 361000;3.福建省风灾害与风工程重点实验室,福建 厦门 361024; 4.厦门理工学院,福建 厦门 361024)
0 引言
随着中国国民经济的发展与桥梁建设水平的提升[1-2],越来越多大跨度跨海桥梁得以建设,随着桥梁跨度的增加,风荷载对桥梁结构影响日益显著[3]。在桥梁没有挡风设施的条件下,桥面风速可达到来流风速的80%以上,特别在沿海地区极端气候[4]条件下,桥面出现高速横风概率较大,货车等大型车辆容易发生侧翻事故,桥面行驶车辆安全问题突出。目前,设置挡风障是减少桥面横风对行驶车辆影响的最有效措施。近些年,Chen、王露等[5-6]利用风洞试验、流体仿真等手段,发现挡风障显著提高了桥面通行车辆稳定性,但并未系统开展挡风障参数对行车稳定性影响规律的研究;Kozmar,Guo,Chu,李波,周奇,陈宁,高剑,丁嘉杰,林晓波,苏洋,詹铠臻等[7-18],在没有车辆的桥梁模型上,测量挡风障后方桥面风场各车道的平均风速剖面图,计算桥面等效风速来评价桥梁挡风障挡风性能,研究了桥梁挡风障高度、孔隙率等参数对桥面风速遮挡效率影响规律,然而,桥面横风直接作用对象为桥面行驶车辆,挡风障参数对桥面行驶车辆稳定性的影响规律与桥面等效风速折减系数评价结果是否一致仍有待研究。因此,开展了桥梁挡风障孔隙率、高度、孔形等参数对于车辆行驶稳定性影响的研究,并与挡风障测速试验研究结果进行对比,检验等效风速折减系数与车辆气动力评价指标结果一致性。
1 试验模型
模型制作除了确保模型与实际尺寸几何相似,及控制加工尺寸误差在2%以内之外,还选用刚度较高的材料,以保证模型须具有足够大的刚度,避免试验过程时出现较大振动,影响试验精度[19]。
1.1 模型安装平台
将桥梁挡风障及车辆模型安装于长为18 m的等截面箱梁平台上,该平台设置了3个宽为3.75 m 的车道,平台如图1所示。桥梁模型几何缩尺比的选择考虑阻塞比的影响,阻塞比ζ[19]按式(1)计算。
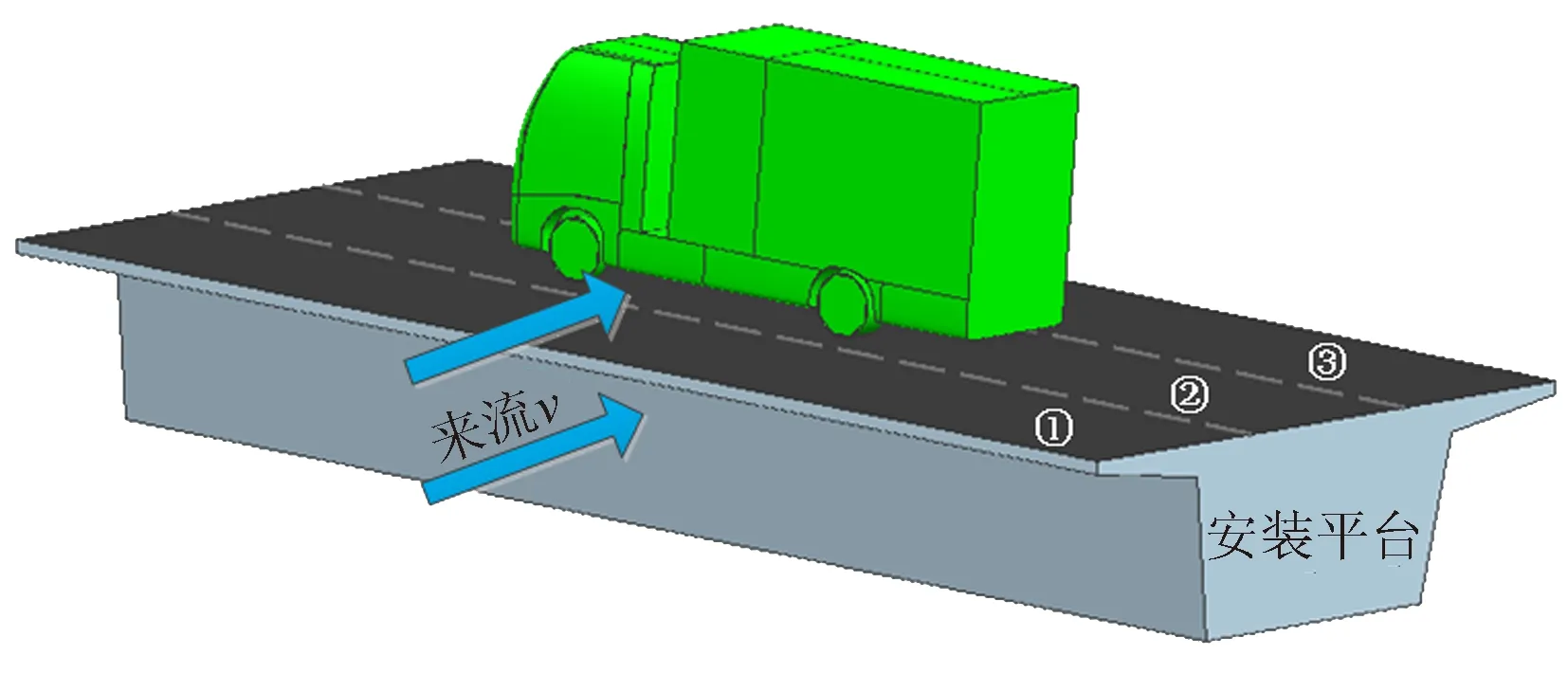
图1 模型安装平台
(1)
式中,Am为风洞试验段的横截面积;Ac为试验模型在试验段横截面的最大投影面积。
模型几何缩尺比设为1∶10,其放置于试验段的最大阻塞率为3.75%,满足小于5%的试验要求。
1.2 挡风障模型
模型主要参数有孔隙率、高度、孔形等。风洞试验证明,50%孔隙率的挡风障遮挡效率既高,又不会大幅降低桥梁气动稳定性;同时,2 m左右高度的挡风障能有效降低桥面风速[16]。故设置10组不同开孔形状的孔隙率为40%~60%,高度为1~3 m模型如图2所示,方案参数见表1。

图2 挡风障模型实物图与试验图

表1 挡风障模型主要参数
1.3 车辆模型
在横向侧风作用下,桥面行驶车辆容易发生侧滑,特别是货车等大型车辆可能发生侧翻等事故。本次研究设计并制作了货车模型进行风洞试验。货车模型采用树脂材料制作而成,几何模型采用与箱梁及桥梁挡风障一致的缩尺比1∶10,车辆模型参数如表2所示,车辆模型及测力试验如图3所示。

表2 货车模型主要参数
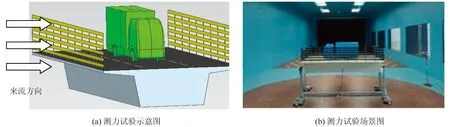
图3 车辆模型实物图与试验图
2 试验设置
2.1 试验条件
测力试验与测速试验均在厦门理工学院XMUT-WT风洞进行。在实际桥梁管理中,当桥面风速达到25 m/s 时,通常采取封桥等交通管制措施以确保行车安全性,为了研究大风条件下挡风障对货车行驶稳定性影响程度,设置实际来流风速为25 m/s工况;同时考虑沿海地区极端气候下桥梁挡风障的阻风效果,设置35 m/s风速工况[17]。试验风速与实际风速应满足相似关系[19],主要有雷诺准则与弗劳德准则,其中,对于桥梁等分离点比较明显的钝体结构,可以忽略雷诺数的不相似对试验结果影响[20]。故,试验风速取值保证弗劳德数相似,弗劳德数计算如式(2):
(2)
式中,g为重力加速度;l为物体特征长度;v为物体运动速度。
2.2 测量位置
车辆测力试验采用的传感器有TFI眼镜蛇脉动风速仪(Series100 Cobra Probe)与ATI六分量高频天平(SI-130-10),仪器主要参数如表3所示。

表3 传感器参数
测速试验采用TFI眼镜蛇三维脉动风速仪测量第②车道中心线车辆模型高度附近处,即0~40 cm 高度的风速剖面图;测点间隔、采样频率与时长分别为2.5 cm,600 Hz,60 s,测点布置如图4所示。
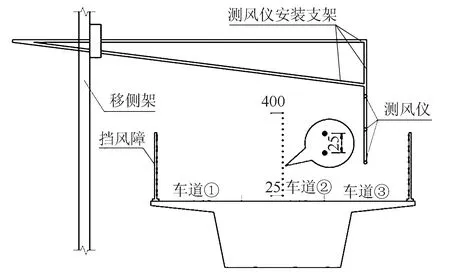
图4 测速试验测点布置图(单位:mm)
车辆模型安装于桥面第②车道,为了避免试验过程中,车辆模型与桥梁接触带来的误差,将车轮与桥面保持2 mm的距离,通过定制立杆将货车与六分力天平连接,车辆模型安装及天平架子如图5所示。

图5 模型安装示意图
3 试验结果分析
3.1 测力试验结果分析
本次试验中测得的数据主要为货车模型的六分力,根据SAE路面汽车空气动力学委员会发布的J1594标准[21],乘用车空气动力学坐标系由右手定则来确定,乘用车空气动力学坐标系如图6所示。SAE标准对作用在车身的六分力定义及计算公式的总结于表4。

图6 汽车空气动力学坐标系

表4 SAE标准对作用在车身上的六分力定义
在横风作用下,车辆稳定性主要受气动侧力、气动升力和侧倾力矩影响[22]。因此,将测力试验测得的气动侧力、侧倾力矩、气动升力数据按汽车空气动力学坐标系转换后取均值,汇总于表5、图7。
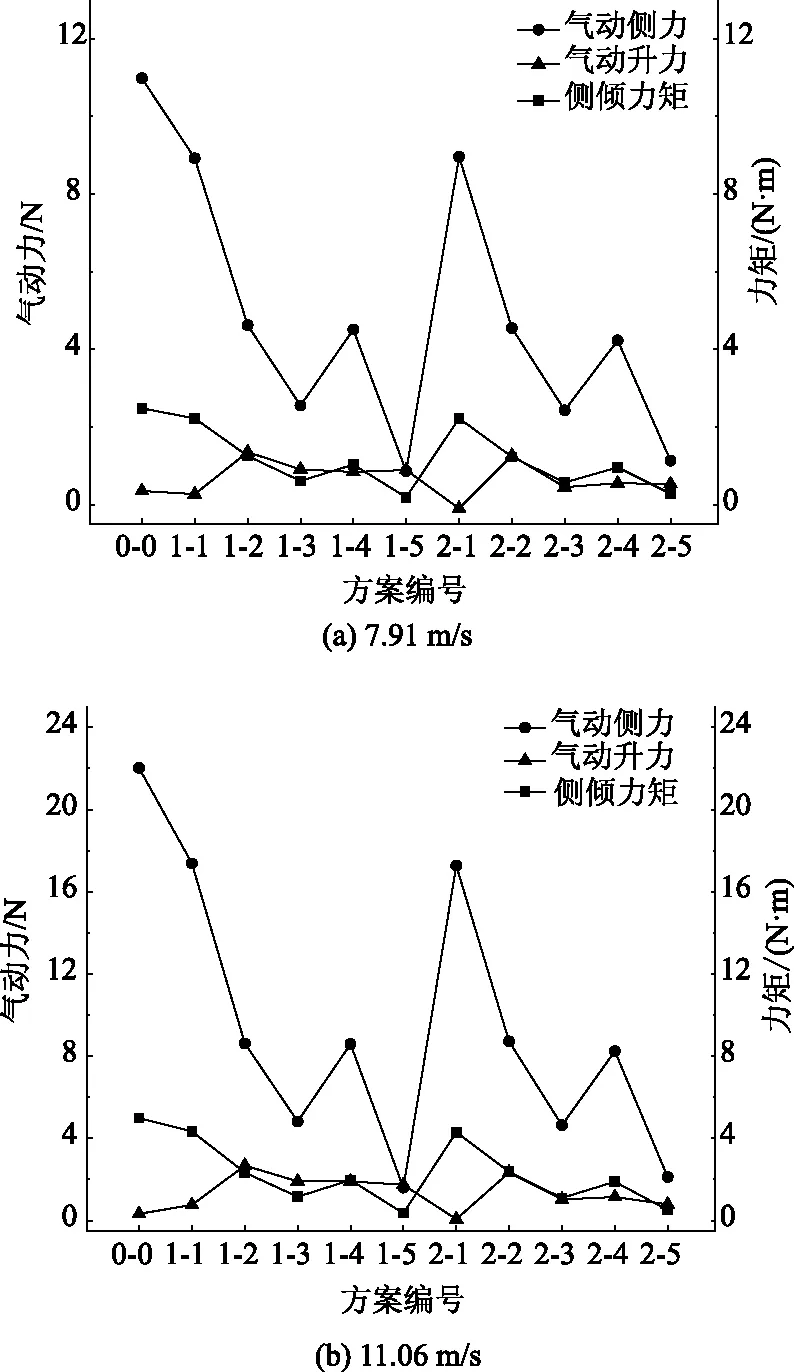
图7 两种风速工况下,各方案气动侧力、气动升力、侧倾力矩对比
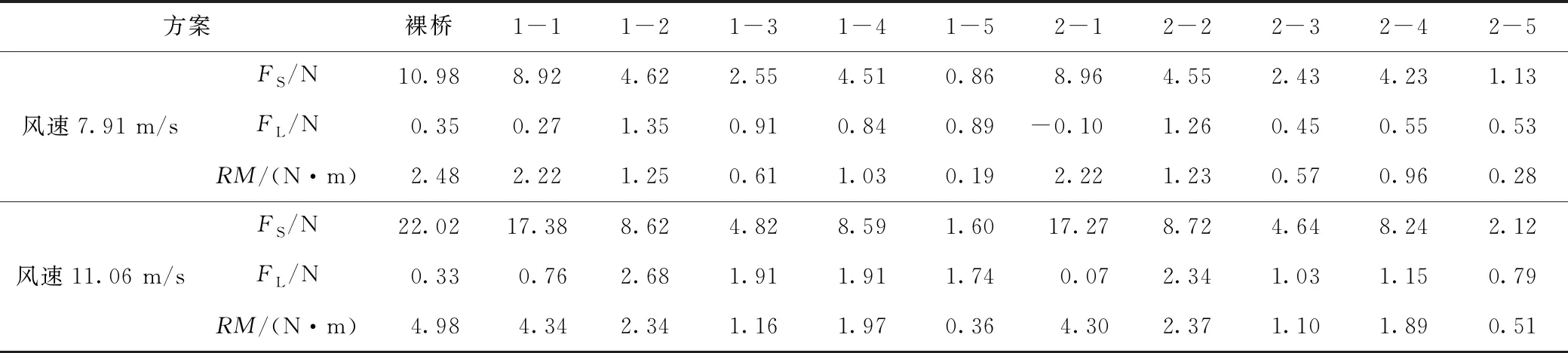
表5 货车模型风洞试验结果汇总
绘制不同参数挡风障后,货车模型测得的气动侧力、升力及侧倾力矩对比图并进行分析。
(1)不同高度、孔隙率障条式挡风障遮挡效率分析
图8为设置孔隙率为50%,高度分别为10,20,30 cm及高度为30 cm,孔隙率分别为60%,40%的障条方案后的测力试验结果对比图。由图8可知:在不同风速横风作用下,模型气动侧力与侧倾力矩规律相近。在同一孔隙率条件下,障条挡风障后方模型侧倾力矩及气动侧力随着挡风障高度的增加而减小;风障高度增加与模型气动侧力降低呈现出非线性关系,在风障高度由0 cm增长至20 cm的过程中,货车气动侧力降低幅值呈现加速状态,而在高度由20 cm增长至30 cm过程中,发现气动侧力降低幅值的速度放缓,这是由于风障顶部的上方存在一定的加速区域,在风障高度较小时,货车迎风面与该区域有重叠部分,使得货车受到气动侧力及侧倾力矩较大,而随着挡风障高度的增加,上述加速区域与货车重叠区域减小,货车迎风面在该区域风压降低,货车受到的力与力矩随之减小。同一高度条件下,障条挡风障后方模型侧倾力矩及气动侧力随孔隙率减小而减小,这是由于障板阻挡来流的面积随着阻塞率的减小而增加,降低了气动侧力及侧倾力矩。货车气动升力随障条高度增加先上升,后下降。这是由于挡风障高度较低时,来流小部分通过障条空隙,而大部分从风障结构顶部上绕流通过后,进入到车底,使得车顶、车底压差较小。对后方车道遮挡高度随着风障高度增加而增加,车顶与车底压差先增大后减小。在不同孔隙率的障条型挡风障后方车道上测得的货车气动升力接近,这是由于风障高度一定时,孔隙率对风速分布影响较小,货车底部、顶部风压变化不大,其受到气动升力大致不变。鉴于风速对遮挡规律影响有限,计算7.91 m/s 下,不同高度方案测得气动侧力、侧倾力矩、气动升力标准偏差分别为2.65,0.66,0.44;不同孔隙率方案测得气动侧力、侧倾力矩、气动升力的标准偏差分别为1.49,0.34,0.03。这表明,挡风障后方车辆气动侧力与侧倾力矩受障条式高度、孔隙率影响大,气动升力值受高度影响大,这是由于孔隙率影响后方气流风速而高度对后方气流分布规律影响较大导致。
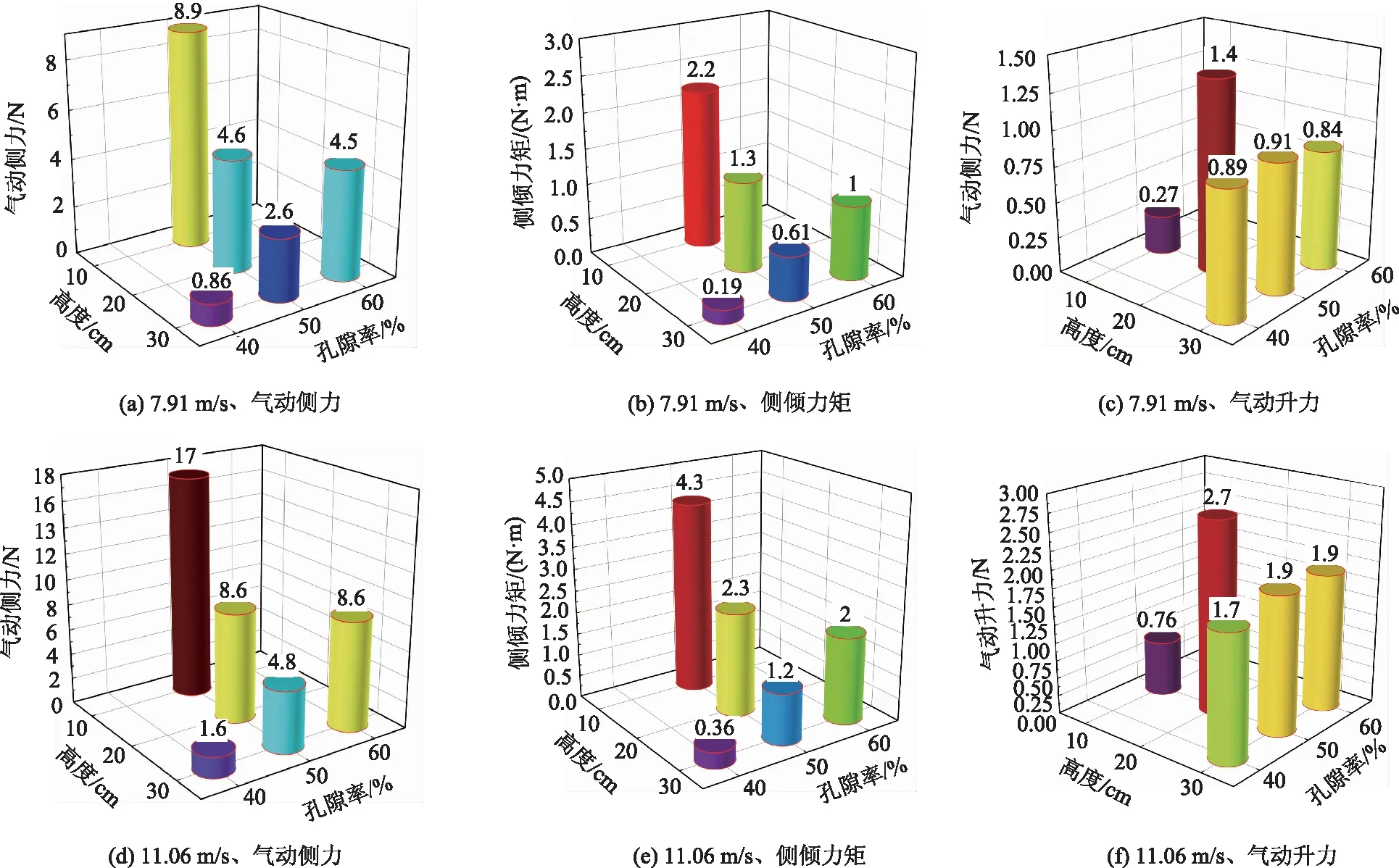
图8 两种风速工况下各障条方案的测力结果对比
(2) 不同高度、孔隙率圆孔挡风障遮挡效率分析
图9为设置不同高度与孔隙率的圆孔挡风障方案后,测得的货车模型气动侧力、升力及侧倾力矩。

图9 两种风速工况下各圆孔方案的测力结果对比
由图9可知:在不同风速横风作用下,测得的货车气动侧力与货车侧倾力矩规律相近。在孔隙率相同时,货车侧倾力矩及气动侧力随高度增加而减小。货车气动侧力随高度增长而降低的幅度具有差异性,在高度由0 cm增长至30 cm过程中,呈现逐步降低的趋势。同一高度条件下,货车侧倾力矩及气动侧力随孔隙率增加而增加。货车气动升力随圆孔挡风障高度的增加呈现出先上升,而后下降的趋势。不同孔隙率的圆孔挡风障后方测得气动升力接近。计算了7.91 m/s下,不同高度圆孔方案后方测得气动侧力、侧倾力矩、气动升力的标准偏差分别为2.72,0.68,0.46;不同孔隙率障条方案后方测得气动侧力、侧倾力矩、气动升力的标准偏差分别为1.27,0.28,0.04。这表明,挡风障后方车辆气动侧力与侧倾力矩受圆孔式高度、孔隙率影响大,气动升力值受高度影响大。
(3)不同开孔形状挡风障遮挡效率分析
图10为桥面各风障方案后,测得的货车模型气动侧力、侧倾力矩及气动升力对比图。
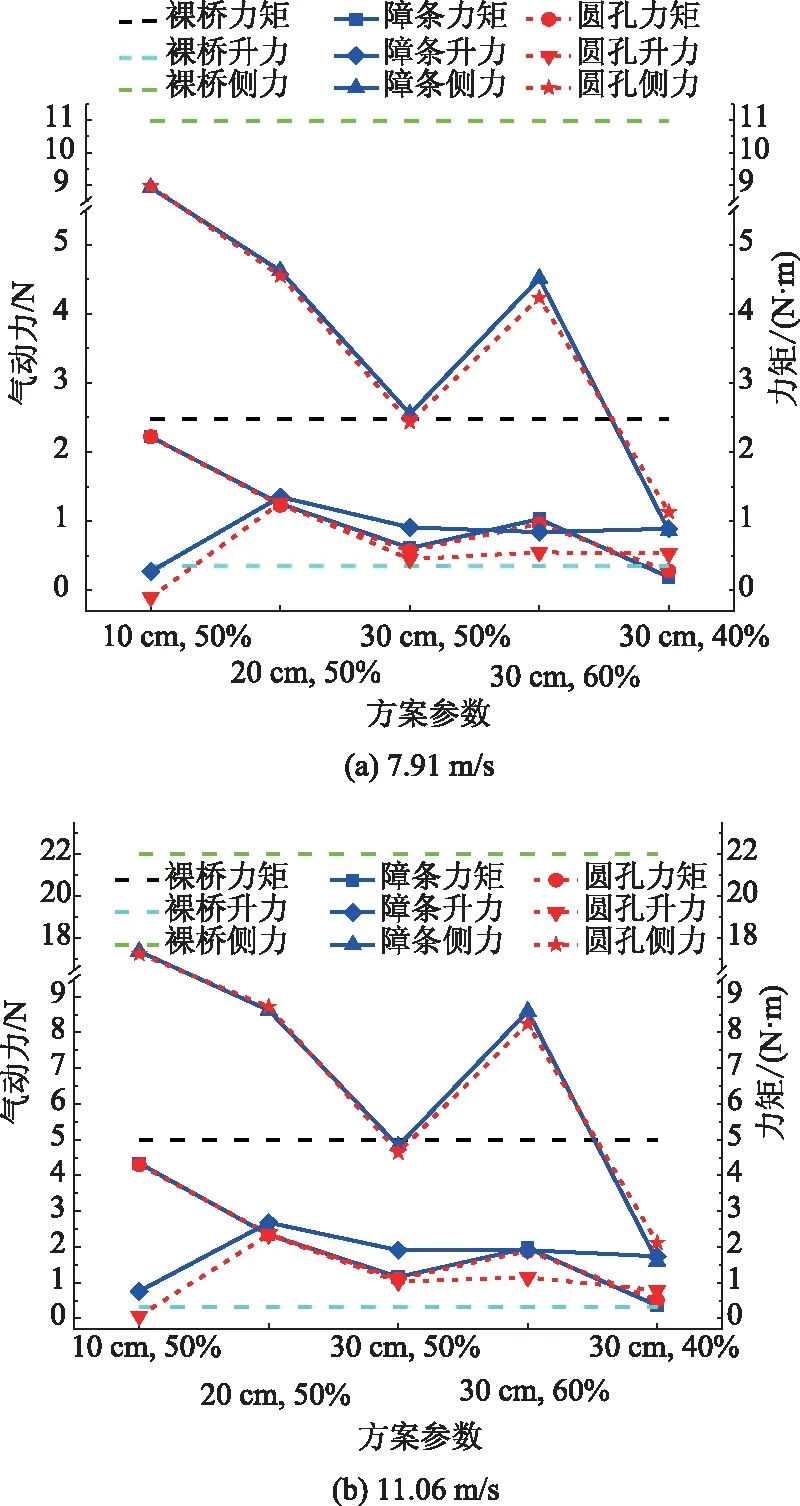
图10 两种风速下,障条与圆孔挡风障后方车辆模型气动侧力、侧倾力矩、气动升力对比
由图10可知,安装挡风障方案能有效降低货车模型的气动侧力与侧倾力矩,但是出现模型气动升力大于裸桥工况的现象,这是由于挡风障对结构高度范围内风场遮挡效果较好,而对模型顶部遮挡效果较差,使得车辆模型上下两侧压差较大造成的。因此,在评价挡风障性能时,需考虑安装挡风障后,桥面风场不同高度处压差变化对车辆气动升力产生的影响。整体上,圆孔挡风障方案遮挡效果优于障条式。
3.2 测力试验结果与流场测速试验结果比对
测速试验得到第②车道中心线0~40 cm高度的平均风速剖面图,根据矩形风剖面和实际风剖面压力总和相等的原则,得到不同挡风障方案的等效风速,将其无量纲后得到折减系数,等效风速折减系数按式(3)[15]计算。
(3)
式中,Zr为风剖面高度范围,取40 cm;u(z)为Z高度处测点的横向风速值;u0为来流风速。两种风速工况下各方案的风速折减系数汇总如表6所示。

表6 两种风速工况下风速折减系数
在桥梁上设置挡风障主要目的是减少桥面侧向横风对桥面行驶车辆的影响,提升桥面车辆在大风天气下的行驶舒适性与安全性。目前,桥梁挡风障采用桥面等效风速折减系数作为挡风性能评价指标,但桥梁挡风障对桥面行驶车辆稳定性的影响规律及其与桥面等效风速折减系数评价结果是否一致?因此,将在不同挡风障方案后方测得的车辆模型的气动侧力、倾覆力矩进行无量纲化获得相应的折减系数,与该处的桥面等效风速折减系数进行比对,鉴于气动升力与车辆底部与顶部局部风场关系密切,应当作为辅助评价指标,故没有参与对比。分别将各量除以裸桥工况下测得的试验值,得到各方案的气动侧力折减系数ηf,侧倾力矩折减系数ηm,等效风速折减系数ηr,将各系数折减系数绘制于图11。

图11 两种风速工况下各方案气动侧力折减系数、侧倾力矩折减系数、等效风速折减系数对比
由图11可知,在不同风速工况下,各挡风障方案的气动侧力折减系数、侧倾力矩折减系数、等效风速折减系数数值接近,偏差集中于0.01~0.10;测力试验折减系数整体偏大,这是由于测速试验的测点位于2个挡风障立柱中心处,挡风障遮挡性能低,使得风速折减系数较大,而在测力试验中,货车长度大于挡风障两个立柱的间距2 m,所以其整体折减系数比较小,这说明采用风速折减系数评价挡风障性能是偏安全的;在挡风障研究与实际设计中对挡风障性能评价时,宜考虑立柱间距与车辆长度的影响。整体上,测速试验与测力试验获得的试验结果是一致的,采用桥面等效风速评价不同挡风障整体性能的优劣是适宜的,而测速试验可借助移侧架实现同一风速下的多点、多车道测量,后续研究可在考虑了桥面风场不同高度处压差变化对车辆气动升力产生的影响后,继续采用该评价方法,以提高工作效率。
4 结论
通过挡风障车辆模型风洞测力试验结果,分析挡风障高度、孔隙率及开孔形状等相关参数对车辆行驶稳定性的影响规律,与挡风障测速试验结果对比,得到如下结论:
(1)安装桥梁挡风障后,车辆气动侧力及侧倾力矩随来流风速的增加而增加,在不同风速来流条件下,气动侧力及侧倾力矩变化规律一致。
(2)安装挡风障后,测得车辆模型气动侧力及侧倾力矩随着挡风障高度增加而减小,随着挡风障的孔隙率增加而变大;车辆气动升力随挡风障高度增加先增加后减小,而与挡风障孔隙率关系不明显。
(3)圆孔挡风障提升车辆稳定性的效果优于障条式挡风障。
(4)采用等效风速折减系数作为挡风障整体效率的评价指标效率更高;然而,需要考虑安装挡风障后,桥面风场不同高度处压差变化对车辆气动升力产生的影响。
文中探究了横风作用下,桥梁挡风障参数对于桥面行驶车辆稳定性影响规律,对比桥梁挡风障车辆测力试验与流场测速试验结果,验证遮挡效果评价指标的一致性,然而未考虑加装挡风障对桥梁结构本身产生的影响,针对具体桥梁风致作用下各挡风障参数对桥梁的气动特性影响规律仍有待进一步研究。

