基于分数阶导数的冻土损伤蠕变模型研究
闫有民, 单静云, 刘志义
(1.公路建设与养护技术材料及装备交通运输行业研发中心, 甘肃 兰州 730030;2.甘肃路桥建设集团有限公司, 甘肃 兰州 730030;3. 甘肃万泰建设工程有限公司, 甘肃 兰州 730030;4.兰州理工大学 土木工程学院, 甘肃 兰州 730050)
0 引言
冻土路基沉降变形随时间的持续发展一直以来都是路基病害的关键问题之一[1-2]。同时,也是公路工程和铁路工程稳定性的潜在危害,对高寒高海拔地区的工程建设、运营及养护造成了一系列的影响[3-4]。因此,精确模拟冻土蠕变行为是目前高寒高海拔地区路基工程亟待解决的关键性问题之一。
迄今为止,研究者们对冻土蠕变进行了大量的试验研究,重点考虑了温度、应力和应变率等因素对冻土时间依赖特性的影响[5-9]。其中,结合蠕变过程中应变率的变化,将冻土蠕变分为衰减蠕变、稳定蠕变和加速蠕变阶段[8]。此外,Zhou等[9]指出,应力在未抵达屈服应力之前冻土也会产生不可逆的蠕变变形。在理论模型方面,往往采用元件模型来构建冻土的蠕变模型[10-11],并通过引入指数函数来实现非线性描述。虽然传统元件模型为模拟冻土蠕变行为提供了基础,但由于弹性元件的完全弹性和塑性元件的纯粹塑性使模型存在一定的局限性。因此,分数阶模型的发展很好地改进了对传统元件模型的限制,并可通过引入变参数效应来实现黏性损伤描述[12]。Liao等[8]使用黏性损伤与分数阶导数建立了温冻土的蠕变模型,并利用试验结果对分数阶蠕变模型的有效性进行了验证。Zhou等[13]结合黏塑性理论与分数阶导数构建了黏性土的蠕变模型。除此之外,分数阶微分作为解释非常规物理现象的一种数学技巧,可解释土体的非正交特性[14-15]。但是,在上述冻土蠕变模型中,没有考虑应力抵达屈服应力之前的黏塑性变形。
然而,在以往的冻土蠕变模型中都忽略了应力抵达屈服应力之前的黏塑性变形,且没有使用分数阶导数来刻画冻土的塑性流动。因此,本研究在已有试验结果的基础上对冻土的损伤效应进行了分析。然后,采用分数阶导数和过应力理论获得了一个可以表征冻土黏塑性行为和损伤效应的黏塑性损伤模型,并采用分数阶梯度描述了冻土抛物线屈服准则的非正交特性。最后,结合发展的黏塑性损伤模型、胡克弹簧和Abel阻尼器构建了一个冻土的分数阶损伤蠕变模型,并使用高温冻土的蠕变试验结果验证了模型的有效性。
1 Caputo分数阶导数
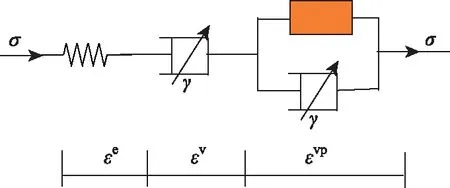
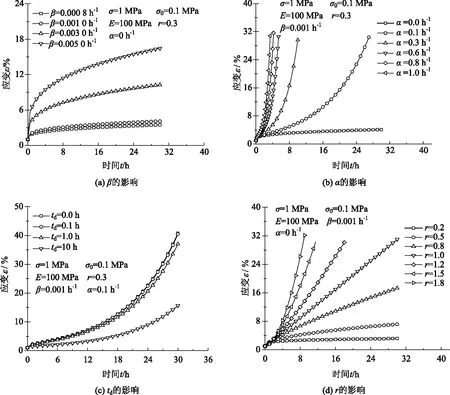
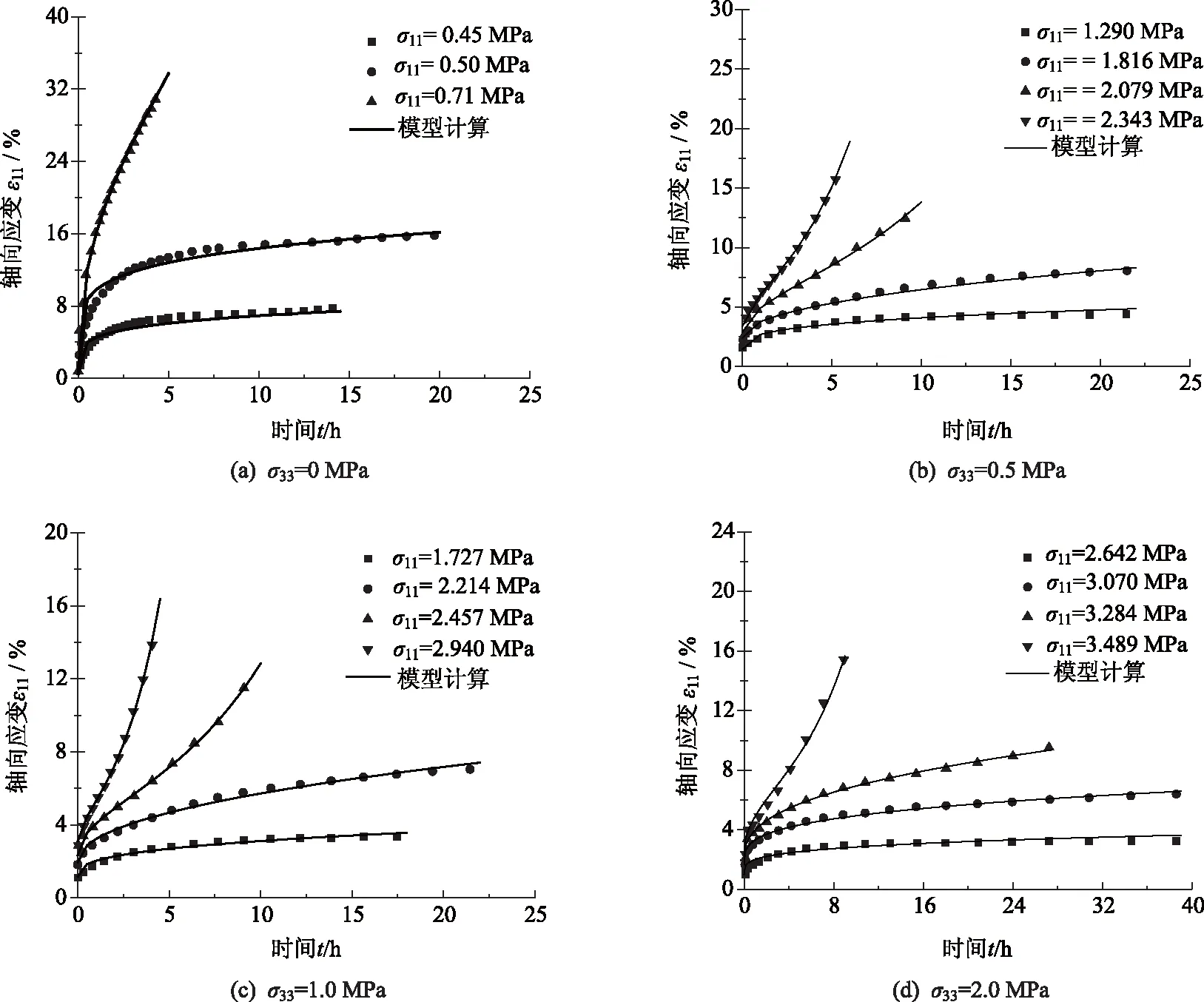
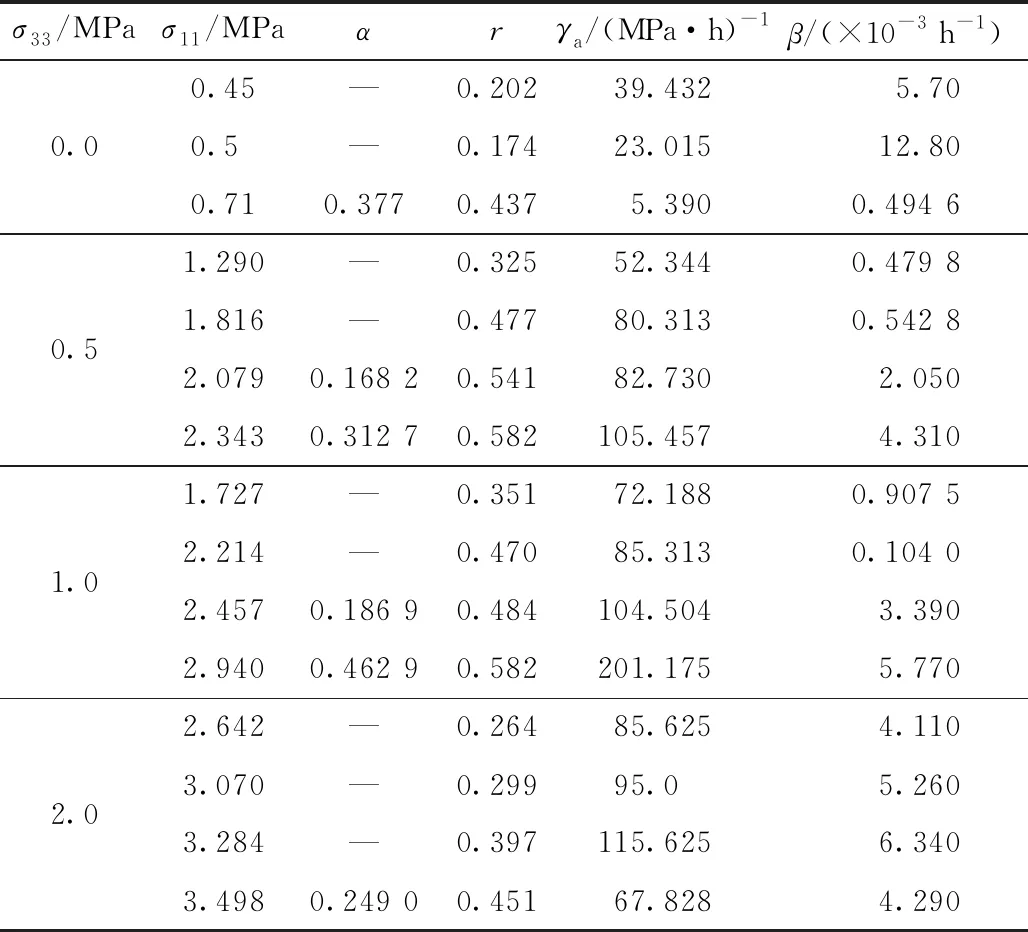
分数阶微分的定义有多种方法,而在构建物理数学模型中应用较为广泛的有:Riemann-Liouville (RL)分数阶微分、Caputo分数阶微分和Risez分数阶微分[16]。其中,Caputo分数阶微分在理论求解方面能够消除常数项对解的影响。因此,下面采用Caputo分数阶导数进行具体研究。Caputo分数阶导数在区间0 (1) 根据式(1)可得到函数f(t)分别为常函数和幂函数时的通解为: (a)f(t)=const时: (2) (b)f(t)=tx时: (3) 损伤力学是通过描述材料的细观机理来反映其宏观响应,是一种从细观唯象理论出发,根据材料自身特性来刻画结构变形和破坏机理的定量分析方法。周宏伟等[12]提出采用体积应变和波速比来衡量损伤因子的大小。Liao等[8]进一步通过最终应变和初始应变来反映温冻土的损伤因子。此外,李鑫等[7]通过损伤因子来表征冻土的弱化效应,以此来预测冻土的加速蠕变行为。 由于应力水平和土颗粒与冰晶体的相互作用,使冻土在触发损伤之后仍然具有继续承载的能力,并对触发损伤的应力、时间产生了明显的影响[7]。因此,对冻土的蠕变曲线(应变ε-时间t曲线)进行分析,具体如图1所示。其中,Ⅰ代表冻土蠕变最基本的形式,且在此应力作用下不发生黏弹性损伤和蠕变破坏;Ⅱ表明冻土在经历了衰减蠕变后,发生损伤稳定蠕变和损伤加速蠕变行为,即认为损伤开始于稳定蠕变的初始时刻,并且整个损伤过程历时较长,因此将其定义为渐进损伤;Ⅲ为应力水平明显大于损伤阀值,几乎不经历稳定蠕变阶段就发生蠕变破坏,且整个蠕变过程历时较短,故称为快速损伤蠕变行为。 图1 冻土蠕变的三种基本形式 结合应变对损伤机理的描述和图1的分析结果,将黏塑性损伤因子考虑为损伤初始应变和最终应变的关系,即: (4) 式中,D为损伤因子,0≤D≤1;ε为应变;εd为损伤初始应变(见图1)。根据式(4)和蠕变试验结果得到损伤因子D与时间te的相互关系。因此,可将式(4)表示为: D=1-e-αte, (5) 式中,α为D-te曲线的拟合参数;te为应变为εd时的时间,即te=t-td。 过应力理论是在Malvern[17]一维模型的基础上发展起来的。在一定程度上,过应力理论也可理解为Bingham模型在三维应力条件下的推广形式。因此,过应力理论不仅有较为完善的理论基础,而且在描述冻土蠕变方面有着较为明显的优势。Zhou等[13]结合传统过应力理论和Riesz-Caputo分数阶导数获得了弹黏塑性模型的解析解。因此,在推广过应力理论的基础上,考虑分数阶导数和损伤效应后,可得到一个黏塑性体的分数阶微分关系: (6) 对式(6)考虑Laplace变换和卷积运算后,得到一般应力状态下黏塑性体的本构关系: (7) 式中,p为平均主应力,且p=1/3(σ1+σ2+σ3);Pa为大气压力。 此处假设黏塑性变形存在于整个加载过程中,并认为黏塑性损伤只有在应力触动黏塑性损伤阀值后,才会发生黏塑性破坏。也就是说,当应力小于屈服应力时(f=0),α=0;当蠕变应力不小于屈服应力时(f>0),α∈(0,1]。 根据冻土屈服准则和强度效应的研究[18],表明冻土的临界状态线不是直线,而是一条抛物曲线。因此,Liao等[8]根据试验结果,给出了一个具有一般性的表达式。因此,为了简化模型,仍然使用抛物线函数来描述冻土的屈服过程: (8) 式中,ω为抛物线函数与平均应力轴左侧交点的横坐标;φ为内摩擦角;c为黏聚力;q为剪应力;f为屈服函数。 结合屈服方程可得到: (9) fq=q+A2, (10) 根据Caputo分数阶导数的运算法则(式(2)和式(3))得到: (11) (12) 根据非正交流动法则与式(11)、式(12)可获得黏塑性流动方向: (13) 图2为非正交黏塑性流动法则在子午面上的演化规律。从图中发现黏塑性流动方向在阶次r∈(0,1)时表现出了明显的非正交性。此外,随着阶次r的减小,非正交性逐渐趋于明显。值得注意的是,式(13)在没有引入新势函数的基础上就实现了黏塑性流动的非正交特性,从而消除了正交流动在土体的限制[19]。 图2 非正交黏塑性流动在子午面上的演化 为了实现元件模型在描述冻土加载过程中的蠕变变形,采用弹簧体、Abel阻尼器和黏塑性体组建了一种分数阶损伤蠕变模型,模型组成具体如图3所示。 图3 分数阶弹黏塑性蠕变模型示意图 根据图3所示,可得到分数阶蠕变模型的应力应变关系分别为: ε=εe+εv+εvp,σ=σe=σv=σvp, (14) 式中,ε,εe,εv,εvp分别为总应变、弹性应变、黏性应变和黏塑性应变;σ为应力,上标“e”,“v”,“vp”分别表示弹性、黏性和黏塑性性质。 因此,一般应力状态下冻土的分数阶损伤蠕变模型可表示为: (15) (16) 式中,G为剪切模量;γa为Abel阻尼器的黏度系数;sij为偏应力张量,sij=σij-pδij;εij(t)为总应变张量。 模型参数中包含弹性参数、黏性体参数和黏塑性参数。由于弹性参数和黏度系数的普遍性,这里主要讨论黏塑性参数对模型计算结果的贡献。黏塑性体主要包含β,α,te和γ这4个参数。 除此之外,发现采用应变能够囊括应力、温度、结构等因素变化对损伤效应的贡献。所以使用损伤初始应变εd与最终应变的比值来刻画黏塑性损伤因子,见式(4)。损伤系数α是此类模型反映材料损伤效应的参数之一,是通过拟合损伤因子与时间曲线确定的。由图4(b)发现黏塑性损伤效应随着α的增大而快速增大,其中,α=0表现为无损蠕变形式。时间te是除系数α之外的另一个损伤参数,表示损伤时间,te通过时间t和td的差值来计算。其中,td是损伤的触发时间(见图1),损伤触发时间td对蠕变曲线的影响情况如图4(c)所示。从图中发现随着td的增大,蠕变速率与应变都有少量的降低。故td会影响蠕变的发展速率与应变量级,但不会对其产生本质影响。 图4 黏塑性体的参数分析 分数阶阶次r作为分数阶模型最主要的一个参数,阶次对蠕变曲线的影响情况如图4(d)所示。从图中发现在阶次r∈(0,1)时可以很好地刻画材料的非线性蠕变行为。但是,在阶次r≥1时应变与时间曲线会出现线性蠕变和蠕变破坏行为。然而,蠕变破坏行为的出现似乎是一个好的结果。 在冻土中,高温冻土作为一种存在范围广、周期长且蠕变效应明显的特殊冻土,对公路工程和铁道工程产生了一系列的不良影响。因此,下面分别采用模型模拟高温冻土的蠕变试验结果。其中,富含冰冻结沙土在-1 ℃的恒温下完成加载,温冻淤泥的试验温度为-1.5 ℃。详细的土性参数和试验结果分别见Yang等[10]和Liao等[8]。 图5为模型计算结果与试验结果的对比情况。其中,图5(a)为模型对富含冰冻结沙土一维蠕变试验结果的模拟情况。富含冰冻结沙土的弹性模量和屈服极限分别为E=90.9 MPa和σs=0.568 MPa,其他参数如表1所示。从图中发现,模型能够较好地模拟富含冰冻结沙土的稳定蠕变、渐进损伤蠕变和快速损伤蠕变行为。图5(b)~图5(d)为模型对温冻淤泥三轴不排水剪切试验结果的模拟情况。其中,温冻淤泥在围压为0.5,1.0 MPa和2.0 MPa下的剪切模量G分别为18.13,20.72 MPa和21.13 MPa。可明显看出,模型计算结果与试验结果具有较高的一致性。此外,相较于传统的元件模型而言,新模型是在推广损伤理论和黏塑性体的基础上提出的,其表征黏塑性行为也存在于屈服面内,且损伤开始于初始稳定蠕变阶段。 图5 模型对温冻土蠕变行为的模拟情况 同时,模型也能较好地模拟温冻淤泥的三维蠕变行为,并且可以刻画土体在屈服之前的黏塑性行为和屈服之后的损伤蠕变行为。此外,根据模型和试验结果的对比,还发现无损蠕变过程包含明显的弹性、黏性变形和少量的黏塑性变形。黏塑性变形会随着应力水平的增加而增加,具体如表1参数β所示,即β会随着应力水平的增加而增加[20]。在土体损伤蠕变过程中,黏塑性变形会随着损伤程度的增加而增加,该现象正好与试验结果相吻合。 表1 温冻土的模拟参数 根据模型对冻土蠕变行为的模拟情况,可以肯定模型在模拟冻土蠕变行为的适用性和有效性。具体为,发现推广后的黏塑性损伤模型可描述冻土屈服前后的黏塑性蠕变行为和损伤效性。除此之外,使用分数阶导数表示了冻土黏塑性流动的非正交特性。因此,认为推广的分数阶损伤蠕变模型消除了传统塑性体纯粹塑性的限制。 (1)依托试验结果对冻土损伤蠕变行为进行了分析,将损伤蠕变分为渐进损伤和快速损伤蠕变。在此基础上,将其进行推广,并根据试验结果发现黏塑性损伤模型能够很好地描述冻土的蠕变破坏行为。 (2)推广的黏塑性理论考虑了冻土在整个加载过程中的黏塑性行为,消除了塑性体纯粹塑性的限制。此外,通过分数阶导数,可直接获得一个非正交黏塑性流动而不需要引入势函数。 (3)根据试验结果和模型计算结果的对比情况,发现模型计算结果与试验结果吻合较好。2 分数阶损伤蠕变模型
2.1 损伤描述
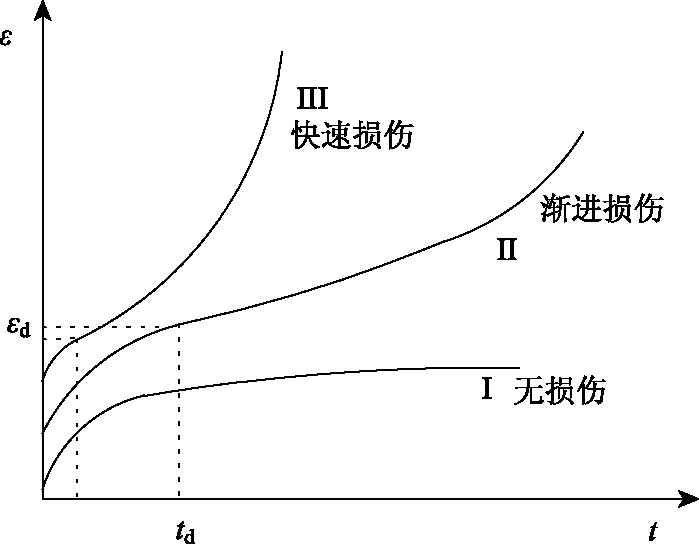
2.2 黏塑性行为
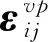
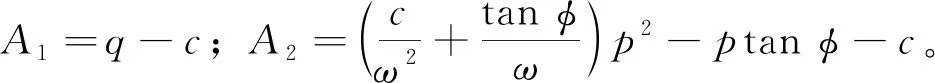
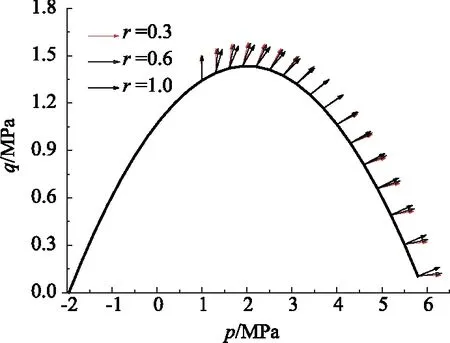
2.3 蠕变模型
3 模型验证
3.1 模型参数分析
3.2 模型计算
4 结论

