高层建筑结构嵌固条件影响研究
范 重,王 晶,,刘 涛,杨 苏,杨 开,王义华,曾德民
(1.中国建筑设计研究院,北京 100044;2.北京建筑大学土木与交通工程学院,北京 100044)
高层建筑结构侧向刚度较小,水平地震和风荷载起主要控制作用。随着城市地下空间利用率不断提高,高层建筑项目通常带有较大面积地下室。地下室不直接承受风荷载作用,且震害经验表明:与地上结构相比,地下室损伤程度较轻。当地下室顶板满足作为上部结构嵌固部位的条件时,可以不考虑地下室结构在地震与风荷载作用下的受力与变形,仅对上部结构进行抗震计算分析,使得结构设计大大简化,该方法在建筑工程设计中得到广泛应用[1-2]。
基于嵌固部位对高层建筑结构抗震设计的重要性,国内外学者对确定嵌固部位的方法进行了大量研究。胡庆昌[3]对上部结构与地下室结构的相互作用进行了开拓性研究,探讨了高层建筑结构的嵌固条件,给出了在水平地震作用下地下室结构基于底部剪力法的计算公式[4]。张朝云[5]提出高层结构地下室嵌固实质上是强度嵌固,地下室结构自身刚度和回填土的约束刚度具有限制结构水平位移的能力,并将上部结构的剪力传递给下部结构。洛杉矶高层建筑结构设计协会在共识文件[6]中提出,当采用不考虑周边土体作用的结构分析模型时,应对地下室楼层质量进行修正。吴汉福等[7]针对为满足绿化覆土等要求、室外地下室顶板低于塔楼首层楼板的情况,提出通过设置加腋等措施后可以将地下室顶板作为上部结构的嵌固部位,在计算结构侧向刚度比时可计入地下室相关范围的影响。Jeong 等[8]针对周边带有地下车库的超高层建筑,分别采用塔楼+投影范围地下室侧向自由、塔楼+投影范围地下室侧向嵌固、塔楼+全部地下室侧向自由和塔楼+全部地下室侧向嵌固4 个计算模型进行了分析比较。
嵌固部位是高层建筑结构力学模型的重要边界条件之一,直接影响如何确定结构高度、抗震等级和地震作用内力调整方法,对计算结果与结构实际受力情况的吻合度以及结构的安全性均具有重要影响。
随着我国城市化的快速发展,地上、地下同时开发,车库、商业和轨道交通等地下空间利用的需求非常迫切,大面积多层地下室得到广泛应用。在确定结构嵌固部位时,经常遇到以下困难:
1)无论将地下室顶板或基础底板作为高层建筑结构的嵌固部位,均无法综合考虑地下室周边土体水平刚度和基础竖向刚度的影响;
2)对不同嵌固条件对高层建筑地上、地下结构整体受力性能以及各类结构构件内力的影响缺乏深入的研究;
3)在邻近塔楼地下室设置大洞口或下沉广场等使用功能,无法对塔楼形成周边约束,对塔楼嵌固作用的影响难以评估。
本文对国内外考虑地下室与周边土体对高层建筑结构地震作用影响分析方面的研究进展进行了回顾,基于塔楼、地下室结构与周边土体的相互作用机理,建立可以考虑高层建筑、地下室与地基基础相互影响的力学模型。在国内外大量研究成果的基础上,根据场地与基础情况确定地下室周边土体弹簧及相应阻尼的计算参数。考察地下室顶板嵌固、地下室周边嵌固、底板嵌固以及土体-结构相互作用共4 种嵌固条件在地震作用下计算结果的合理性,研究土体介质剪切波速与塔楼高宽比的影响。针对塔楼周边开洞的可行性问题,研究塔楼单侧洞口长度对整体结构与结构构件受力性能的影响。
1 上部结构、地下室与地基基础计算模型
1.1 嵌固部位定义方法
通过地下一层侧向刚度与首层侧向刚度之比,控制地下室结构的侧向变形,使其侧向变形可以忽略,框架柱、抗震墙底部塑性铰发生在地下室顶板标高之上,地下一层相应的框架柱或抗震墙保持不屈服。为实现首层柱底先于地下室构件屈服的设计理念,可以采用增大地下室顶板梁、柱配筋等抗震构造措施。当结构满足嵌固条件时,计算模型仅需考虑地面(±0.000 标高)以上结构侧向刚度与地震惯性力的影响,在进行弹塑性时程分析等复杂计算时,可以大大减小计算分析工作量,故此在工程中得到广泛应用。
为使嵌固部位对上部结构具有良好的约束作用,根据我国现行《建筑抗震设计规范》(GB 50011-2010)[1]的规定,当地下室顶板作为上部结构的嵌固部位时,结构地上一层的侧向刚度不宜大于相关范围地下一层侧向刚度的0.5 倍。与此相近,根据我国现行《高层建筑混凝土结构技术规程》(JGJ 3-2010)[2],高层建筑结构整体计算中,当地下室顶板作为上部结构嵌固部位时,地下一层与首层侧向刚度比不宜小于2,计算地下室结构楼层侧向刚度时,可考虑地上结构投影范围以外地下室相关范围(地上结构外扩不超过三跨的地下室)的结构。当结构的等效剪切刚度比不小于2 时,即视为满足嵌固条件,可以仅考虑地下室顶板以上高层建筑的地震作用[2]。根据我国现行设计标准,在确定高层建筑的嵌固部位时,并未考虑地下室周边土体对结构水平变形的约束作用。
1.2 带地下室高层建筑结构计算模型
高层建筑结构在风荷载、地震等水平力的作用下,将发生显著的侧向变形,水平剪力与倾覆力矩将进一步传递到地下室、基础与土体,而地下室结构侧向刚度通常较大,并且受到周边土体的约束。多年以来,土体与结构相互作用(SSI)的影响受到广泛关注,国内外学者进行过大量研究工作。Takewaki 等[9]采用平面桩-土-结构分析模型,讨论了土体与结构相互作用对结构自振周期、塑性铰分布的影响,表明基底刚性假定对结构可能较为不利。Mylonakis 等[10]通过比较单自由度基础嵌固模型和基础有限刚度模型的地震响应,指出基底嵌固边界条件整体上偏于保守,局部偏于不安全。Carbonari 等[11]分析了采用桩基础的框架-剪力墙结构在地震作用下考虑地基-基础相互作用对结构非线性特性的影响,结果表明:基础转动是造成结构层间位移响应增大的主要原因,基础刚度对框架和剪力墙的剪力分担率也存在一定影响。Torabi 等[12]采用三维半无限地基有限元模型,进行软土地基与结构相互作用影响分析,表明矩形平面结构在短方向的自振周期、基底剪力以及倾覆力矩受到的影响比较显著。傅学怡等[13]基于有限基础刚度计算模型,研究基础刚度对高层建筑地震作用与效应的影响规律,较好解释了汶川地震中底层框架柱破坏的原因。范重等[14]同时考虑桩基础竖向刚度与地下室周边土体水平刚度的影响,对不同高宽比剪力墙结构的分析结果表明:考虑基础与土体刚度后,在地震作用下地下室结构的层间位移角显著增大,当结构高宽比大于4 时,水平剪力作用方向可能发生改变。
与研究取得大量进展的情况相反,在国内外考虑地基基础与结构相互作用分析的设计标准与工程实例并不多见。我国《城市轨道交通结构抗震设计规范》(GB 50909-2014)[15]中规定,在进行城市轨道交通结构设计时需要考虑结构-桥墩下桩基础与土体的相互作用,静力分析时将土体等效为非线性弹簧,动力分析时除桩-土相互作用弹簧外,可以进一步采用等效阻尼器描述地震波能量的辐射效应。美国ATC 40[16]和ASCE 41-13[17]中均给出了多种基础形式-土体相互作用的简化计算模型。太平洋地震工程研究中心在其研究报告中[18]提出考虑上部结构、地下室与周边土体相互作用的“浴缸模型”,在地下室的侧面与底面设置弹簧和阻尼器模拟土体的作用,将与地面运动相同的作用于基础底面,并对侧壁进行相同的激励。戚承志等[19]结合核电站建筑抗震研究进展,较为全面地回顾了结构与地基相互作用研究的发展历程,分析比较了采用实体有限元模拟地基的直接法与采用弹簧与阻尼器模拟地基的子结构法(集中参数分析模型)各自的特点。在美国《安全相关核结构地震分析和评价》(ASCE 4-1998)[20]和我国《核电厂抗震设计标准》(GB 50267-2019)[21]中,均给出了集中参数分析模型计算土体介质刚度与阻尼的方法。
为了深入考察嵌固条件对高层建筑结构的影响,较为准确地模拟塔楼、地下室与地基基础的相互作用,本文结合高层建筑在发生地震时以惯性作用为主的受力特点,采用弹簧和阻尼器描述土体介质与结构的相互作用。
1.3 考虑土体-结构相互作用的计算模型
1.3.1 基本假定
在考虑塔楼、地下室与周边土体相互作用时,采用以下基本假定:
①将地下室周边的土体等效为并联的水平非线性弹簧与阻尼器,将基础与土体等效为并联的竖向非线性弹簧与阻尼器;
② 考虑塔楼与地下室结构的刚度和质量;
③在地下室底部进行水平方向地震激励。
1.3.2 结构布置与构件尺寸
抗震设防烈度为7 度,设计基本地震动加速度值为0.1g。设计地震分组为第二组,建筑场地类别为Ⅲ类,场地特征周期为Tg=0.55 s。50 年重现期的基本风压为0.50 kN/m2,地面粗糙度类别为C 类。
带有地下室高层建筑结构的平面布置如图1所示,塔楼位于建筑平面的中部。地下室外轮廓尺寸为92.4 m×92.4 m,地下室共3 层,层高均为4.0 m。塔楼平面尺寸为42 m×42 m,框架柱柱距为8.4 m,核心筒平面尺寸为19.6 m×19.6 m。塔楼高度分为84 m、168 m 和252 m 三种情况,相应的高宽比为2、4 和6,各层层高相同。塔楼的主要控制参数见表1。
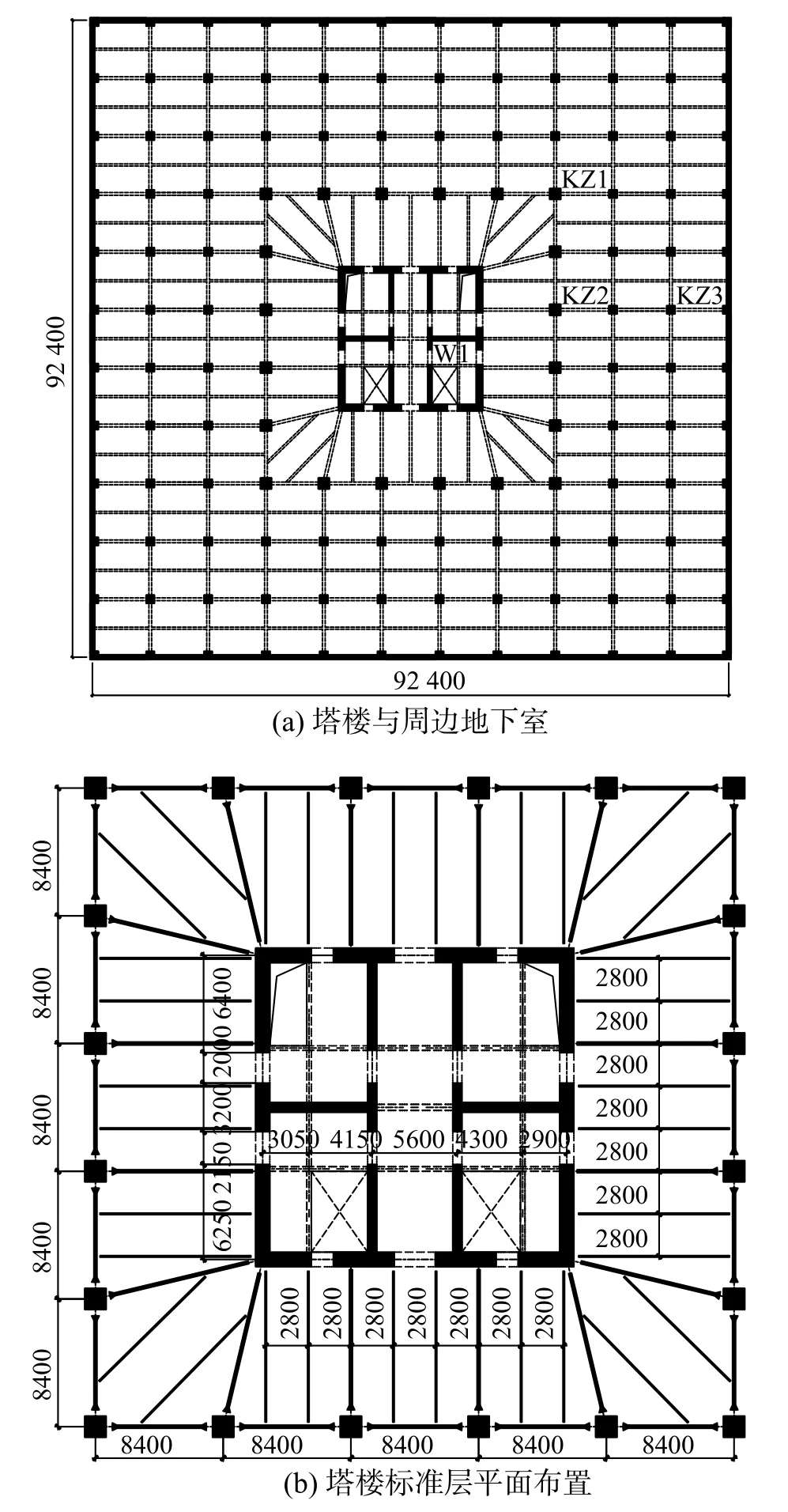
图1 带有地下室的高层建筑 /mmFig.1 High-rise building with basement

表1 塔楼的主要控制参数Table 1 Key parameters of the towers
塔楼采用型钢混凝土框架-核心筒混合结构体系:核心筒采用钢筋混凝土剪力墙;框架柱采用型钢混凝土构件,十字形钢骨;框架梁与楼面梁均为H 型钢梁,材质为Q355B。核心筒外楼板厚度均为120 mm,采用钢筋桁架楼承板;核心筒内为现浇混凝土楼板,厚度均为150 mm。各塔楼主要结构构件的截面尺寸与材质如表2~表4 所示。

表2 H=84 m 塔楼结构构件截面尺寸与材质Table 2 Sectional dimensions and materials of structural members of H=84 m tower
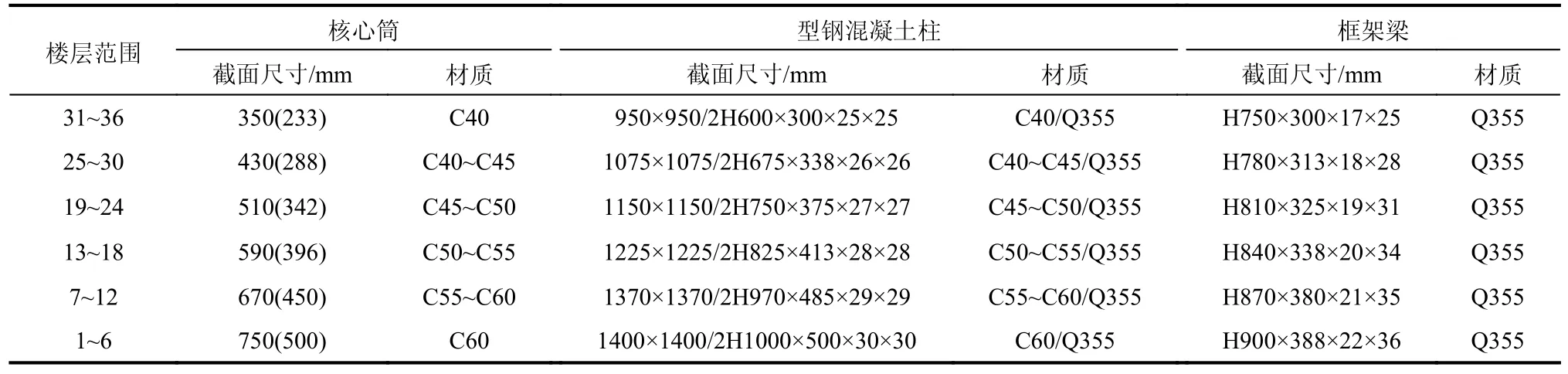
表3 H=168 m 塔楼结构构件截面尺寸与材质Table 3 Sectional dimensions and materials of structural members of H=168 m tower
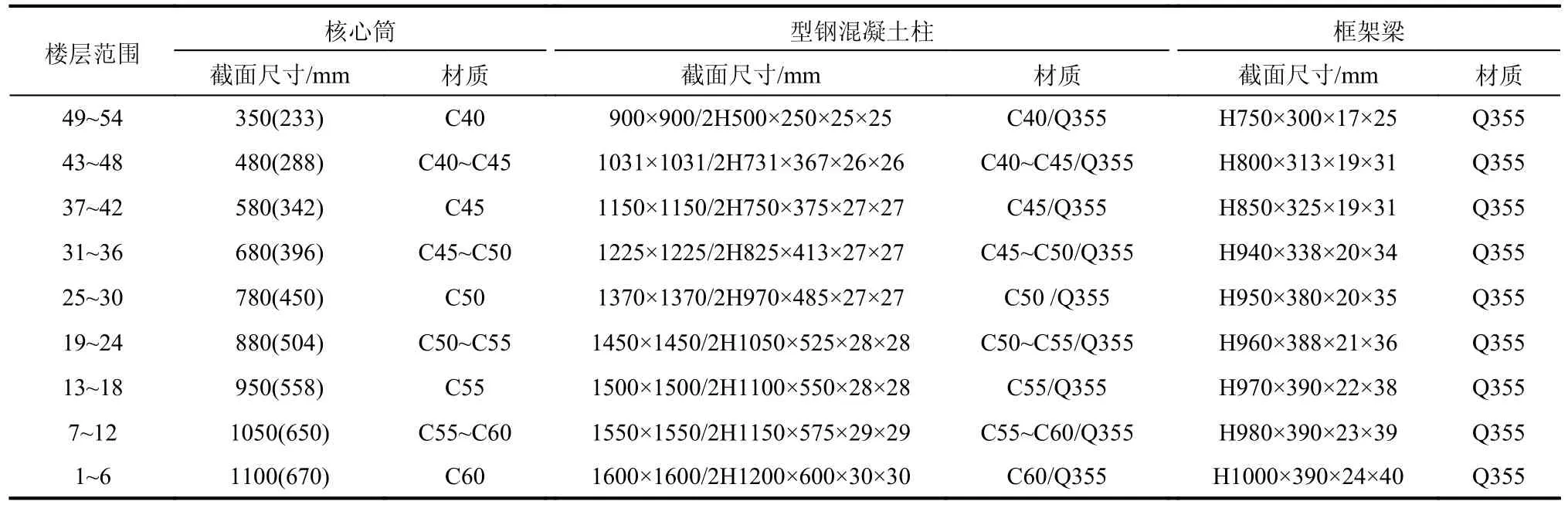
表4 H=252 m 塔楼结构构件截面尺寸与材质Table 4 Sectional dimensions and materials of structural members of H=252 m tower
塔楼投影范围地下室顶板厚度为180 mm,周边地下室顶板厚度为250 mm,其余各层地下室楼板厚度为150 m,混凝土强度等级均为C30。地下室外墙、框架柱、框架梁及次梁的截面尺寸和材料强度等级见表5。塔楼采用钻孔灌注桩基础,纯地下室部分采用天然地基。18 层塔楼底板厚度1.6 m,36 层塔楼底板厚度2.5 m,54 层塔楼底板厚度3.4 m,纯地下室部分底板厚度均为700 mm,混凝土强度等级均为C35。
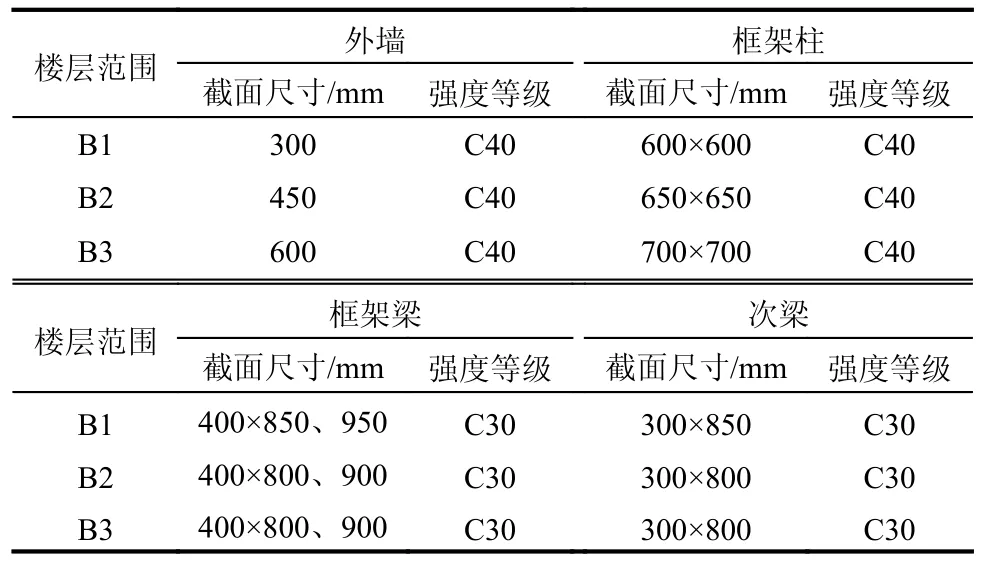
表5 塔楼周边地下室主要结构构件的截面尺寸与材质Table 5 Sectional dimensions and materials of structural members of basement around the tower
1.3.3 计算模型编号与分析软件
为了考察假定嵌固条件与地下室周边土体、地基基础的刚度和阻尼对结构受力性能的影响,本文共采用如下四种类型的计算模型:
模型M1——地下室顶板嵌固模型,假定上部结构嵌固于地下室顶板,整体计算时不考虑地下室;
模型M2 ——地下室周边嵌固模型,假定上部结构与地下室均嵌固于基础底板,地下室顶板处的水平位移为零。通过对地下室各楼层施加水平约束(令楼板位移Ux、Uy和转角RZ为零),限制地下室各楼层的水平变形;
模型M3——底板嵌固模型,假定上部结构与地下室均嵌固于基础底板,不考虑地下室周围土体的约束作用;
模型 M4——土体-结构相互作用模型,考虑基础有限刚度及地下室周边土体的约束作用,将地下室周围土体简化为水平弹簧与阻尼,将桩基础与土体简化为竖向弹簧与阻尼。阻尼与土弹簧并联,土弹簧只受压、不受拉。由于基础底板存在较大的水平摩擦力,假定基础底板与土体之间不发生水平滑移。模型M1~模型M4 的计算简图如图2 所示。
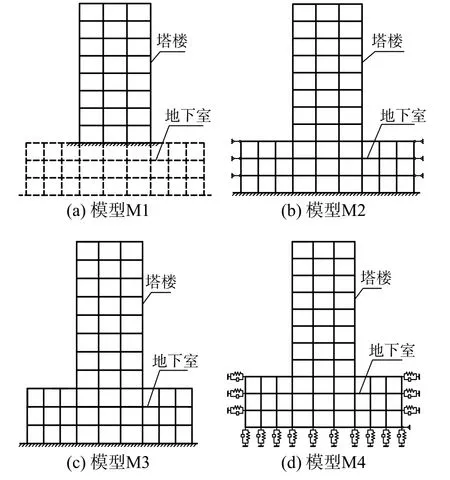
图2 不同嵌固条件结构的计算模型Fig.2 Analytical models of structures with different embedded conditions
本文采用多高层建筑结构有限元分析软件ETABS 软件[22],对带有地下室的高层结构进行地震作用下的时程分析。
2 土弹簧与阻尼器参数取值
2.1 水平弹簧刚度
在进行地下结构抗震设计设计时,可以通过在地下室周边和底部设置弹簧,模拟土体的作用[21]。在确定地下室外侧土弹簧刚度时,需要综合考虑岩土类别和密实度等因素的影响。根据《核电厂抗震设计标准》(GB 50267-2019)[21],当不考虑地基介质动力参数的频率相关性时,水平弹簧的等效刚度可由下式计算:
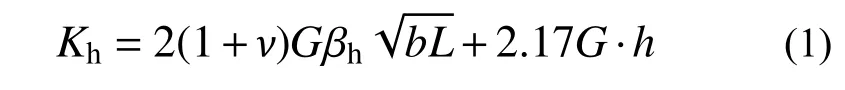
式中:G 和ν分别为地基介质的平均剪切模量和泊松比;b和L分别矩形基础运动方向和运动正交方向的边长;h为基础底面以上地基介质层的厚度;βh为与基础边长有关的计算系数。
在水平地震激励下,土体介质的剪切模量G可由其密度和均匀地基半无限空间剪切波的传播速度确定[23]:

式中:ρ 为土体的密度;vs为土体的剪切波速。
根据钱七虎[24]的研究成果、《建筑抗震设计规范》(GB 50011-2010)[1]和相关工程经验,可以近似确定土体密度与剪切波速的关系。参照《地下结构抗震设计标准》(GB/T 51336-2018)[25]和《城市轨道交通岩土工程勘察规范》(GB 50307-2012)[26],常见土体的刚度——基床系数如表6 所示。由表6 可知,土体的基床系数变化范围很大,对于普通建筑地下室,其水平基床系数一般在30 MPa·m-1~60 MPa·m-1。
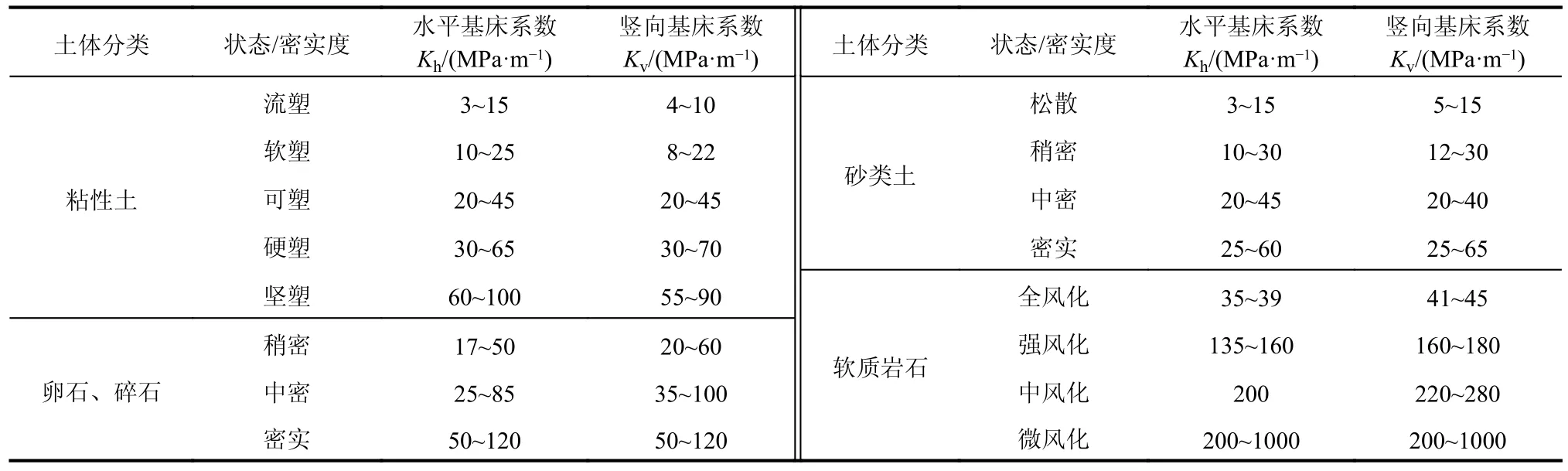
表6 常见土体的基床系数Table 6 Foundation bed coefficient of common soil
2.2 竖向弹簧刚度
纯地下室荷载很小,通常可以采用天然地基。纯地下室部分基础的竖向基床系数,可参照《核电厂抗震设计标准》(GB 50267-2019)[21],其竖向弹簧的等效刚度可由下式计算:
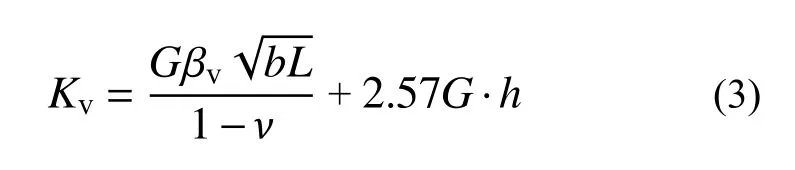
式中,βv为与基础边长有关的计算系数。由式(2)和式(3)可知,竖向弹簧的等效刚度与土体剪切波速的平方成正比。
当地质条件良好、持力层可以满足承载力特征值要求时,高层建筑也可以采用天然地基。此时应结合考虑回弹再压缩后的沉降量,综合确定用于抗震分析的竖向基床系数。
对于我国大部分地域,天然地基无法满足高层与超高层建筑对地基稳定性与沉降量控制的要求,故此高层建筑大多采用桩基础。对于带有多层地下室的高层建筑,由于基础底板与土体之间的摩擦力以及地下室周边土体的约束作用,基础底板的侧向变形很小。故此,可以忽略桩顶的水平变形,仅考虑桩的竖向变形。
桩顶在竖向力作用下产生的竖向变形δ 包括桩身材料的弹性压缩变形δc以及桩端沉降δs两部分[27],桩顶竖向变形s可由下式计算:
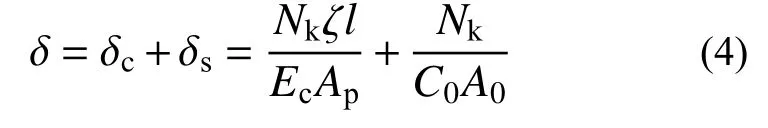
式中:Nk为单桩承担的重力荷载代表值;ζ 为桩身轴向压力传递系数,取0.5~1.0,摩擦桩取小值,端承桩取大值;l为桩的入土深度;Ec和Ap为桩身弹性模量和截面面积;C0为桩底面地基土竖向抗力系数;A0为桩底土压力分布面积,对于端承桩,A0为单桩底面面积,对于摩擦型桩,A0为有效扩散面积。
桩基础沉降量受到很多因素影响,如建筑高度、下卧层岩土工程性质、桩距、是否采用后注浆工艺等,端承桩以桩身压缩变形为主要,沉降量较小;摩擦桩桩端以下土层变形显著,沉降量较大。根据大量工程经验,高层建筑基础的最终沉降量一般在30 mm~80 mm。在进行地震作用计算分析时,可认为基础在结构自重作用下的沉降已经全部完成,故此在估算基础竖向刚度时,可以考虑回弹再压缩效应对竖向刚度的提高作用。
当塔楼采用桩基础时,竖向基床系数Kv可由下式进行估算:
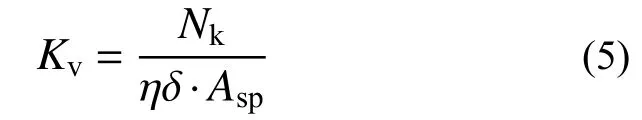
式中:Asp为单桩负担荷载的面积;ηδ 为考虑回弹再压缩效应后桩基的等效竖向压缩变形,η 为小于1.0 的修正系数。
2.3 阻尼系数
在进行桩-土相互作用分析时,主动土压力与被动土压力差异很大,通过设置阻尼器不但可以弥补单纯采用弹簧模拟土体力学性能的不足,还能够反映地震能量向地下室周边半无限场土体介质的逸散效应。土体的阻尼比远大于上部结构的阻尼比,在进行时程分析时,考虑土体介质阻尼的影响非常重要。
迄今,很多学者对半无限空间地基动力阻抗函数计算方法进行了研究。杜守继等[28]通过对8 种代表性地基阻抗函数表达式进行对比,考察地基阻抗函数随土体剪切波速的变化以及对单自由度结构质点水平加速度及底板摆动加速度的影响。刘晶波等[29]基于三维波动方程推导了三维粘弹性人工边界的法向与切向边界方程,研究了时域粘弹性人工边界的数值模拟技术。李锦华等[30]在进行地基土阻尼计算方法探讨时,回顾了不考虑体系频率相关性的阻抗函数经验公式,表明阻尼常数主要与土体密度和土体剪切模量相关。金井清等[31]针对地下结构的圆形基础,给出等效阻尼系数及附加质量的计算方法。土体的阻尼比与岩土类别、密实度等紧密相关,工程常见土体阻尼比的范围为0.3~0.1。
根据美国结构工程师协会标准(ASCE 4-1998)[20]和我国《核电厂抗震设计标准》(GB 50267-2019)[21],当采用集中参数分析模型进行地基与结构相互作用分析时,非频率相关的水平等效阻尼系数可由下式计算:
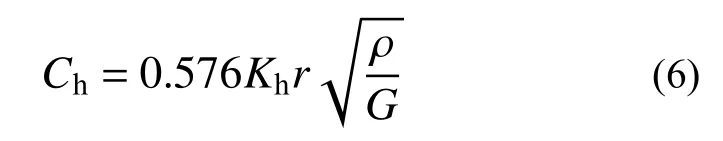
式中,r为矩形基础的回转半径,可由下式确定:
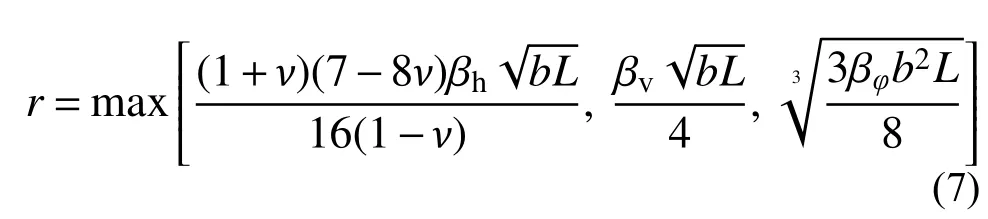
式中,βφ为与基础回转半径有关的计算系数。
非频率相关的竖向等效阻尼系数可由式(8)计算:
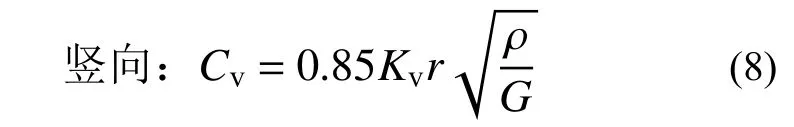
由式(1)~式(3)、式(6)和式(8)可知,土体的等效阻尼系数大致与土体介质的剪切波速成正比。当采用桩基础时,首先根据其竖向基床系数由式(3)确定相应的剪切波速和土体密度,再由式(8)计算其竖向等效阻尼系数。需要注意的是,此时式(7)和式(8)中的L、B和r应为塔楼基础的平面尺寸和回转半径。
2.4 集中参数法计算参数取值
综合第2.1 节~2.3 节弹簧刚度与阻尼的取值方法,主要基于土体的剪切波速,确定纯地下室和塔楼的相关计算参数(L=b=92.4 m,h=12 m)。弹簧基床系数和单位面积阻尼系数随土体剪切波速和密度的变化情况见表7。

表7 计算采用的土体参数Table 7 Soil parameters used in calculation
3 嵌固条件影响分析
3.1 结构动力特性与地震波
为了考察嵌固条件对结构受力性能的影响,分别对地下室顶板嵌固(模型M1)、地下室周边嵌固(模型M2)、底板嵌固(模型M3)和土体-结构相互作用(模型M4)4 种计算模型进行在多遇地震下的时程响应分析。
模型M1~模型M4 的前3 阶自振周期见表8。由表8 可知,地下室顶板嵌固模型M1 的前3 阶自振周期最短;底板嵌固模型M3 的自振周期微有增大,但与模型M2 非常接近;土体-结构相互作用模型M4 的前2 阶平动自振周期显著加长,但扭转自振周期T3变化不大。
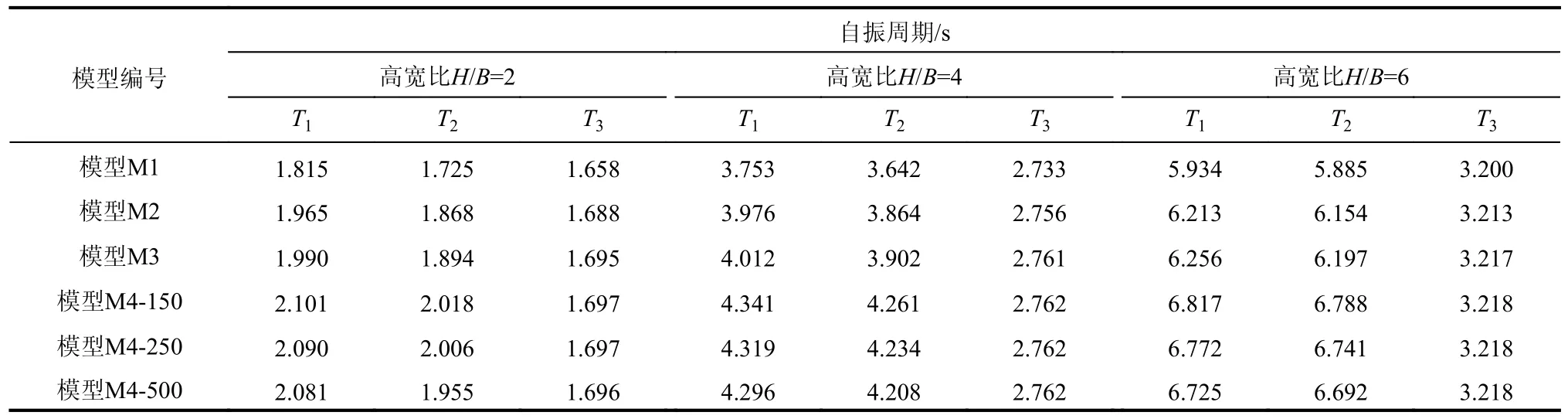
表8 计算模型的自振周期Table 8 Natural vibration periods of the analytical models
为了考察结构在地震作用下响应的规律,避免天然波反应谱差异较大的影响,根据场地条件与结构的动力特性,共选取7 条水平方向的人工波,地震加速度时程记录如图3 所示。由图3可知,每条地震加速度时程的谱曲线与《建筑抗震设计规范》(GB 50011-2010)[1]的反应谱曲线均具有较好的一致性,7 条波反应谱曲线的平均值与规范谱吻合良好。
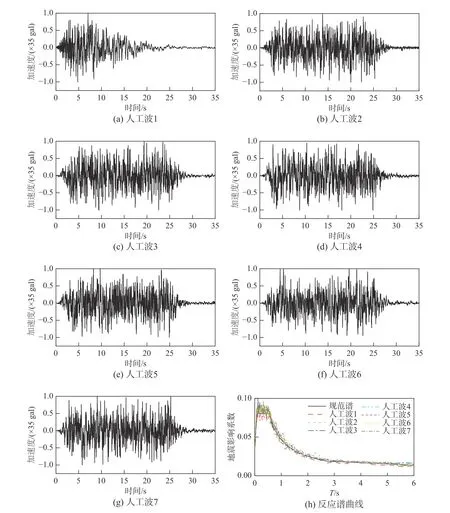
图3 地震加速度时程与反应谱曲线Fig.3 Seismic acceleration time-history records and response spectrum curve
由于计算模型在X方向与Y方向的情况非常接近,为叙述简明起见,以下仅给出X方向的分析结果。此外,本文结果均为在7 条地震波作用下结构内力或位移响应最大值的平均值。
3.2 水平剪力
在7 条地震波作用下,塔楼重力荷载代表值与首层剪重比如表9 所示。由表9 可知,塔楼重力荷载代表值GE的增速大于高宽比H/B的增速;当高宽比为2.0 时,计算模型M1~模型M3 在首层的剪力V较为接近,其中模型M3 在首层的剪力最大;计算模型M4 在首层的剪力小于计算模型M1~模型M3 剪力平均值约13.5%;随着地下室周边土体剪切波速增大,首层的剪力微有增大。随着塔楼高宽比增大,剪重比显著减小,计算模型M4在首层的水平剪力与计算模型M1~模型M3 的水平剪力逐渐接近。
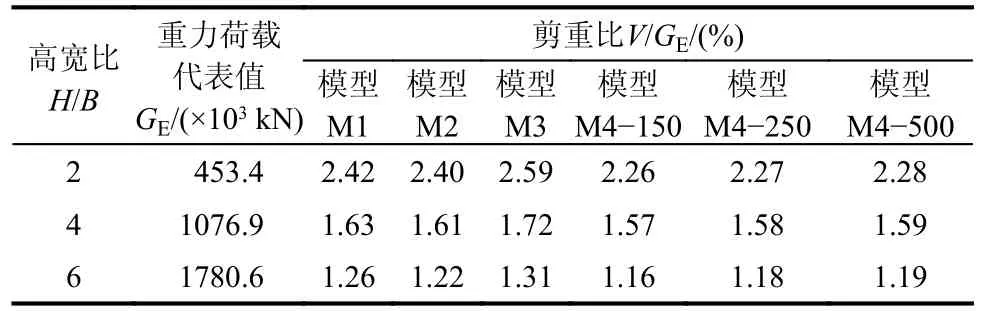
表9 地震作用下塔楼首层的剪重比V/GETable 9 Shear-weight ratio V/GE at the first floor of the towers under earthquake
在7 条地震波作用下,高宽比H/B=2、4、6 时水平剪力沿塔楼高度的分布情况见图4 和表10。由图4 和表10 可知,模型M1 在塔楼底部采用理想嵌固条件,地震力由上至下逐渐增大,在首层达到最大值;模型M2 在地下室顶板及以下楼层的水平位移受到约束,水平剪力在B1 层达到峰值,在B2 及以下楼层水平剪力迅速减小,底层剪力仅为峰值的4.6%~9.1%;模型M3 结构嵌固于基础底板,地下室周边自由,此时地上各层水平剪力与计算模型M1、模型M2 接近,但由于地下室面积远大于塔楼的投影范围,结构的侧向刚度与质量均大于塔楼,故此地下各楼层的水平剪力增速加快。
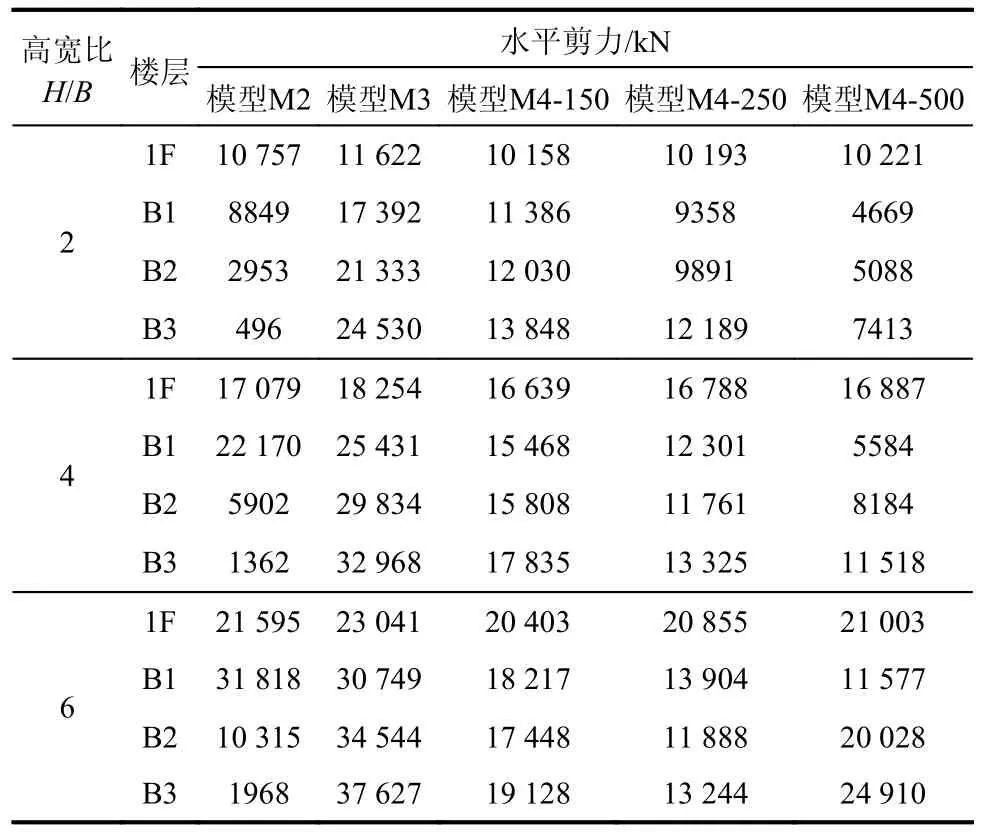
表10 在地震作用下首层与地下室的水平剪力Table 10 Lateral shear force at the first floor and basement under earthquake
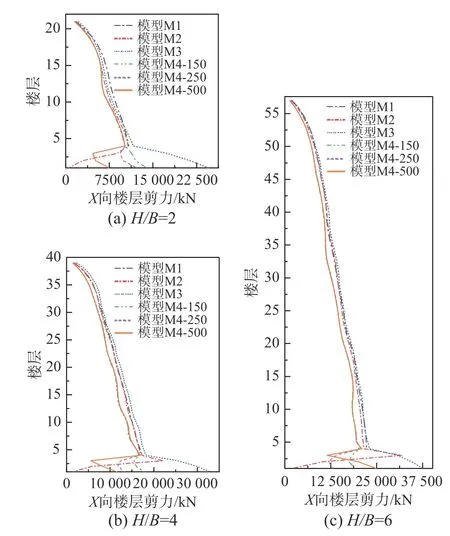
图4 7 条地震波作用下结构的水平剪力Fig.4 Horizontal shear force of the structures under 7 seismic waves
考虑土体-结构相互作用的计算模型M4 动力特性发生变化,在7 条地震波作用下,塔楼水平剪力在首层达到峰值,与模型M1~模型M3 相比水平剪力可减小10%左右,剪切波速对塔楼水平剪力的影响可以忽略。在地下室高度范围,受到周边土体弹簧和阻尼的约束作用,H/B=2 时模型M4-150 地下室楼层水平剪力的增速减小;随着剪切波速增大,在运动方向地下室上部土体的约束作用增强,B1 层水平剪力显著减小;但在运动反方向地下室下部受到撬力的影响,B2 层及以下楼层的水平剪力反而增大。随着高宽比增大,这种效应更为明显。
3.3 层间位移角
在7 条水平地震波作用下,H/B=2、4 和6 时层间位移角沿结构高度的分布情况如图5 所示。由图5 和表11 可知,当高宽比为2 时,模型M1 的最大层间位移角为1/1892,在各计算模型中塔楼的层间位移角最小;模型M2 塔楼的最大层间位移角为1/1853,地下室的层间位移角均为零;模型M3 塔楼的最大层间位移角为1/1771,层间位移角略大于模型M2,B1 层的最大层间位移角为1/16548,虽然地下室的侧向变形很小,但不再为零;模型M4 塔楼的最大层间位移角为1/1675,显著大于模型M1~模型M3,地下室最大层间位移角为1/15419,大于底板嵌固模型M3。随着土体剪切波速增大,结构的层间位移角有所减小。塔楼高宽比H/B=4 和6 时层间位移角情况与H/B=2时类似。
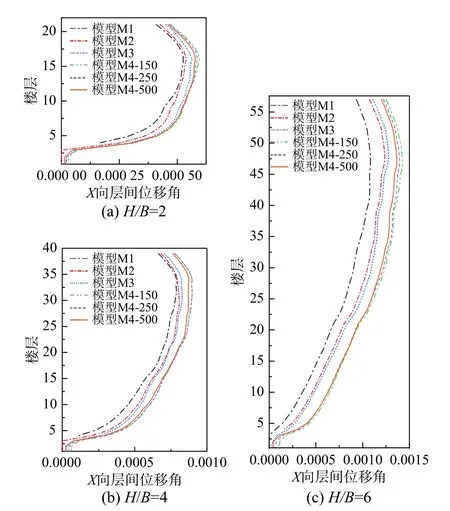
图5 7 条地震波作用下结构的层间位移角Fig.5 Inter-story drift radio of the structures under 7 seismic waves
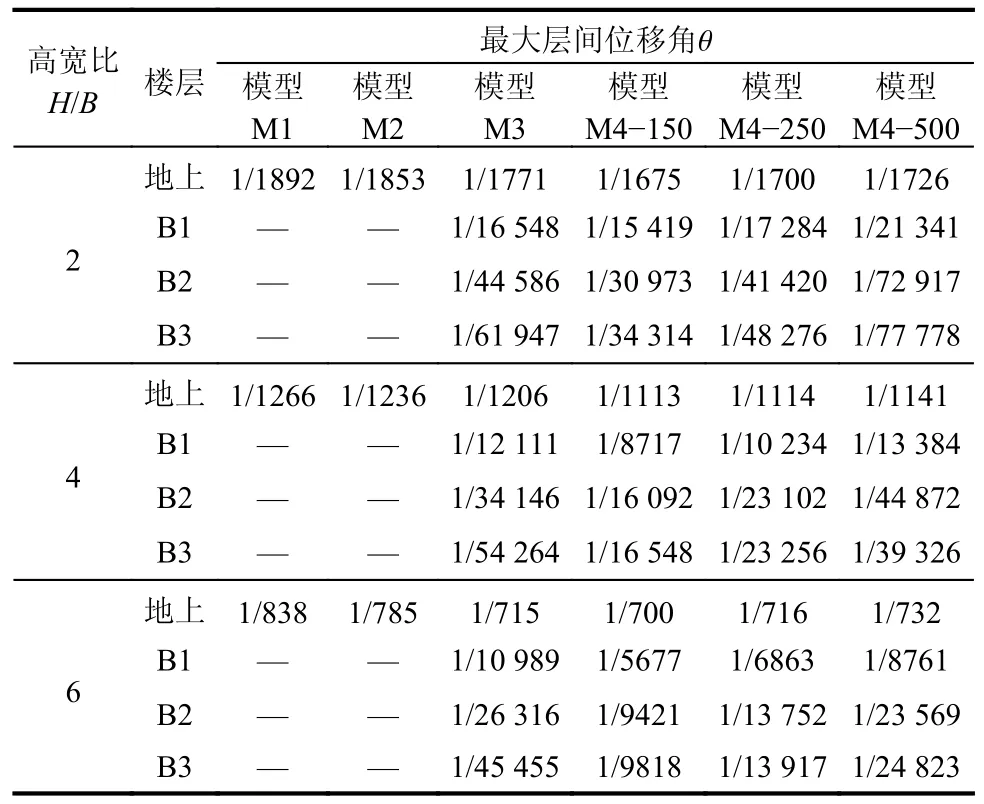
表11 在地震作用下塔楼与地下室的最大层间位移角θTable 11 Maximum inter-story drift ratio θ of the tower and basements under earthquakes
3.4 构件内力
1)核心筒墙肢剪力
在7 条水平地震波作用下,塔楼核心筒墙肢W1(图1(a))的水平剪力见图6 和表12。由图6 和表12可知,对于计算模型M1~模型M4,地面以上楼层墙肢的水平剪力上小下大,在2 层达到峰值,首层受到室外土体的约束作用水平剪力突然减小,但在B1 层又达到最大值,B2 层以下楼层水平剪力迅速减小;模型M1~模型M4 墙肢水平剪力分布的规律大致相同。土体剪切波速对塔楼核心筒墙体内力有一定影响,随着土体剪切波速增大,墙肢剪力略有增大。
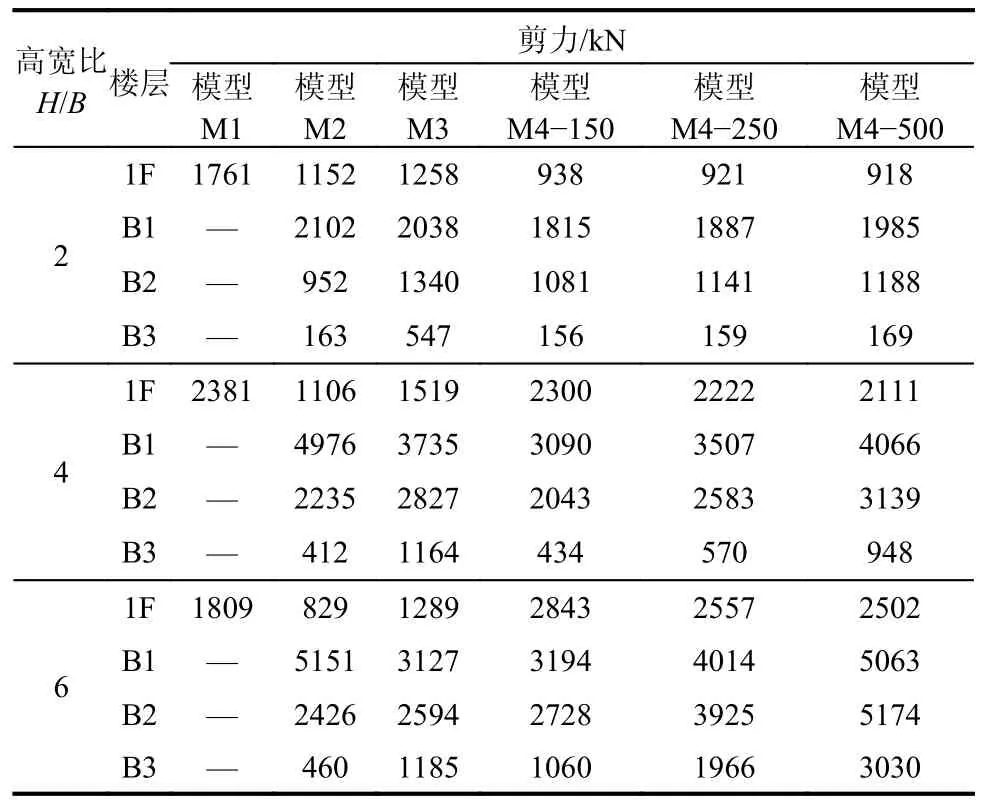
表12 地震作用下核心筒墙肢的剪力Table 12 Shear force of the tower column under earthquakes
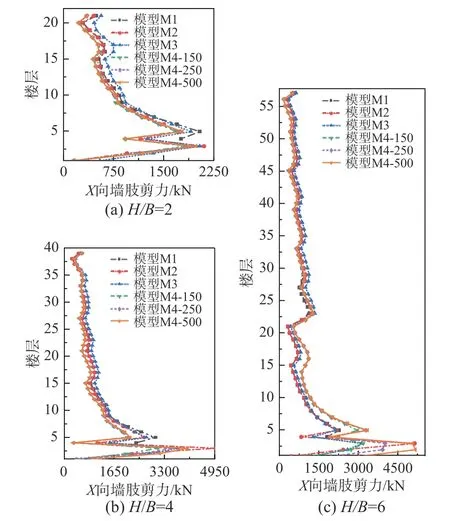
图6 墙肢剪力随土体介质剪切波速的变化Fig.6 Variation of shear force of the wall with shear wave velocity of soil medium
2)框架柱剪力
在7 条水平地震波作用下,塔楼框架柱KZ1(图1(a))的水平剪力如图7 所示。由图7 可知,对于计算模型M1~模型M3,框架柱的水平剪力在2 层以上变化较为平稳,在首层突然增大至峰值;在地下室高度范围内,模型M2 和模型M3 框架柱KZ1 的剪力先迅速减小,而后又有所增大。模型M4 框架柱KZ1 在塔楼下部的水平剪力略小于计算模型M1~模型M3,在塔楼上部水平剪力大于计算模型M1~模型M3;由于受到周边土体的约束作用,地下室高度范围内框架柱的水平剪力室剧烈震荡,水平剪力的峰值远大于地面以上的塔楼。
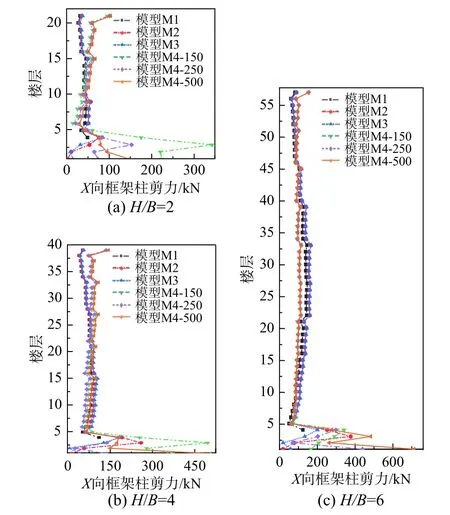
图7 框架柱剪力随土体介质剪切波速的变化Fig.7 Variation of shear force of frame column with shear wave velocity of soil medium
3)地下室外墙弹簧反力分布
在7 条水平地震波作用下,X轴地下室外墙在地震作用方向弹簧反力的分布如图8 与表13所示。由图8 和表13 可知,在地下室顶板部位弹簧反力最大,随着楼层深度增大,弹簧反力逐渐减小;随着土体介质剪切波速提高,弹簧水平反力相应增大;随着塔楼高度增大,弹簧的水平反力显著增大。
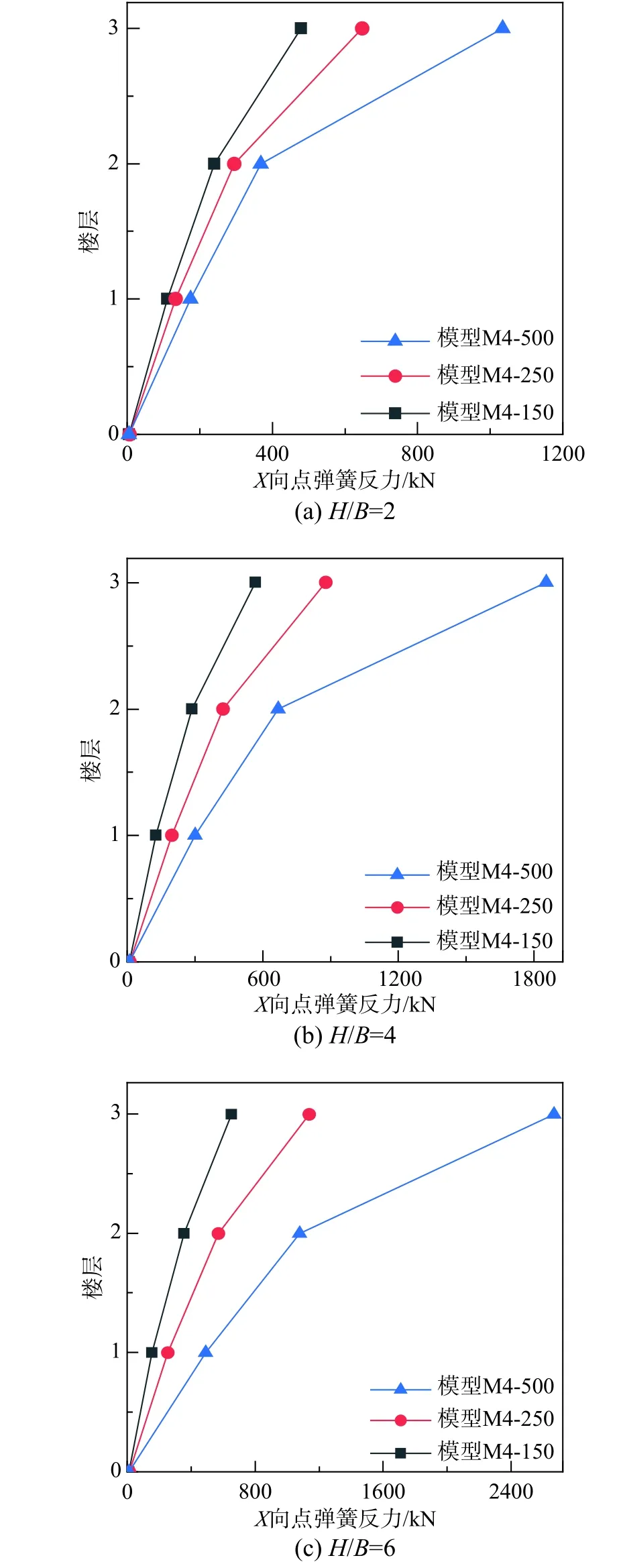
图8 地震作用下地下室外墙弹簧反力的分布Fig.8 Distribution of spring reaction force on basement wall under earthquakes
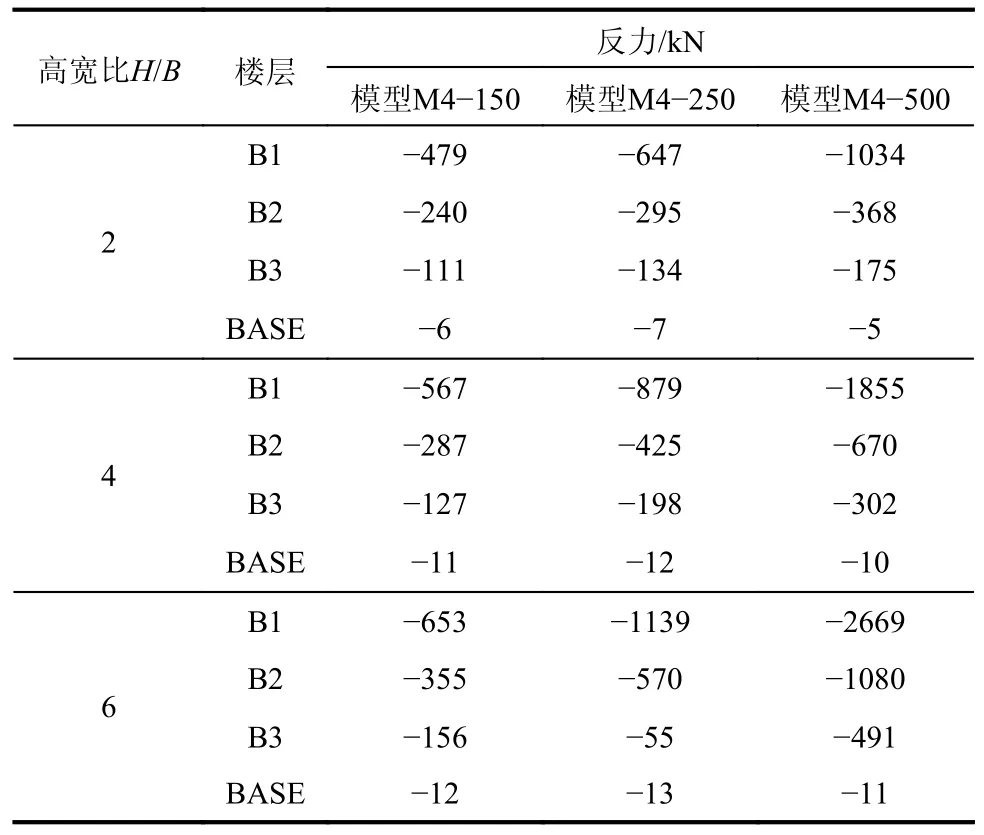
表13 在地震作用下地下室外墙弹簧的反力Table 13 Spring reaction force on basement wall under earthquakes
4 塔楼非周边约束影响分析
4.1 洞口尺寸参数
由于地下车库出入口车道、下沉广场等功能的需要,在高层建筑周边地下室设置尺寸较大的洞口常常难以避免。当塔楼为非周边约束情况时,对其受力性能的影响迄今缺乏系统的研究。
为了考察塔楼周边洞口大小的影响,将洞口边长与塔楼边长之比作为高层建筑单边的洞口长度比λ:

式中:LO为洞口的长度;BO为塔楼在洞口方向的边长。
当塔楼单侧设置通高的地下广场时,地下室开口位置与相应的洞口长度比λ 如图9 所示,采用考虑土体-结构相互作用模型M4 进行计算分析。为了叙述简明起见,仅给出土体介质剪切波速vs=250 m/s 时的计算结果,其他剪切波速时的情况非常类似。首层及以下各层楼板采用壳单元,网格剖分尺寸为1 m。
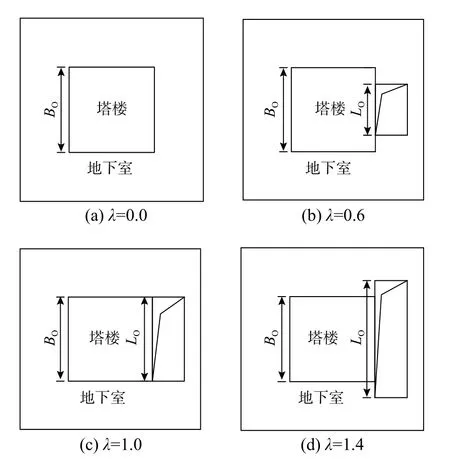
图9 塔楼非周边约束计算参数Fig.9 Coefficient of the tower buildings with nonperipheral constraints
4.2 结构整体指标
4.2.1 自振周期、楼层剪力与层间位移角
非周边约束塔楼结构的动力特性见表14。由表14 可知,当塔楼高宽比H/B=2~6 时,塔楼周边地下室洞口对结构自振周期的影响极小,随着地下室洞口长度比λ 增大,结构自振周期保持不变或微有增大,但变化幅度可以忽略。
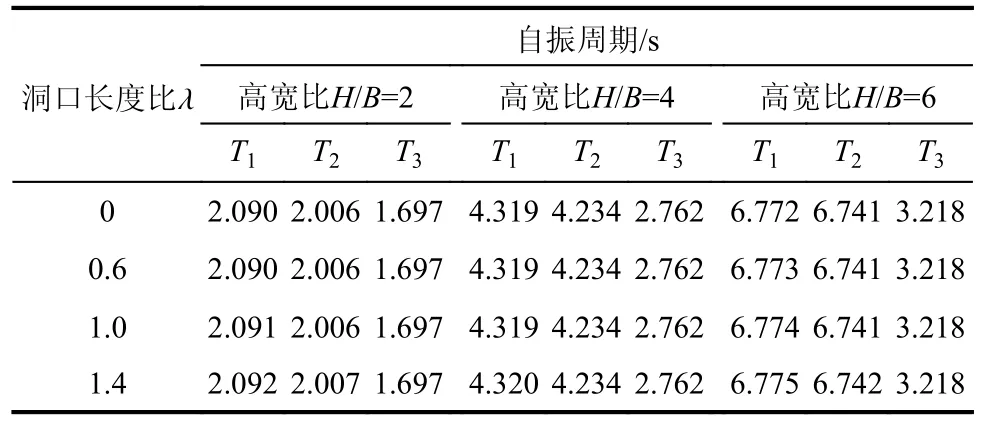
表14 非周边约束塔楼的自振周期Table 14 Natural vibration period of non-peripheral constraint tower
在7 条地震波作用下,非周边约束塔楼首层的水平剪力如表15 所示。由表15 可知,当塔楼高宽比H/B=2 时,随着洞口长度比λ 增大,塔楼首层水平剪力随之减小,但减小幅度不大;当洞口长度比λ 为1.4 时,X方向剪力减小约1.53%,Y方向剪力减小约0.42%。随着塔楼高宽比增大,塔楼首层水平剪力减小的幅度略有增大,最大减小幅度(X方向)为2.14%。
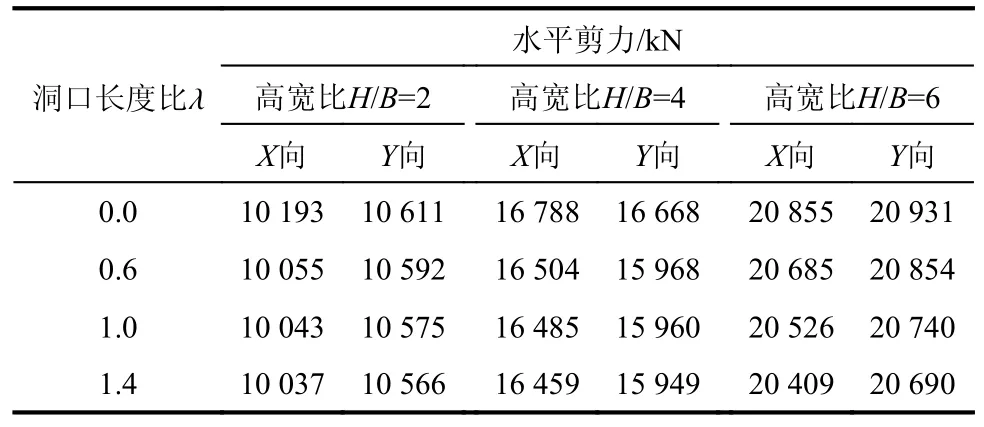
表15 非周边约束塔楼首层的水平剪力Table 15 Horizontal shear force on the first floor of nonperipheral constraint tower
在7 条地震波作用下,非周边约束塔楼的最大层间位移角见表16。由表16 可知,当塔楼高宽比H/B=2 时,随着洞口长度比λ 增大,塔楼在洞口方向(X方向)和无洞口方向(Y方向)层间位移角的增幅均很小,其变化幅度可以忽略。随着塔楼高宽比增大,塔楼在洞口方向(X方向)的层间位移角稍有增大,但增大幅度不超过2%,在无洞口方向(Y方向)层间位移角基本保持不变。
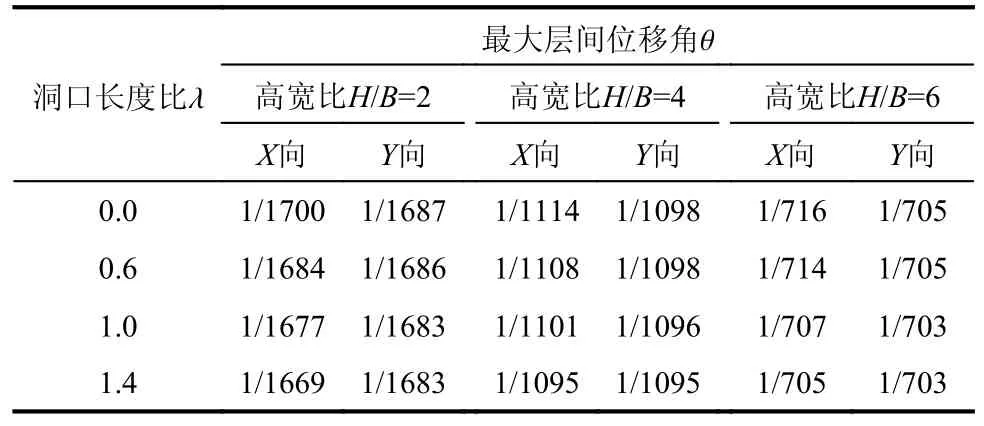
表16 非周边约束塔楼的最大层间位移角Table 16 Maximum inter-story drift ratio of non-peripheral constraint tower
4.3 构件内力
1)剪力墙
在7 条地震波作用下,非周边约束塔楼核心筒墙肢W1(图1(a))的水平剪力如表17 所示。由表17可知,当塔楼高宽比H/B=2 时,随着洞口长度比λ 增大,首层墙肢W1 在洞口方向(X方向)水平剪力增大,无洞口方向(Y方向)水平剪力基本保持不变。随着塔楼高宽比增大,首层墙肢水平剪力值相应增大,在洞口方向(X方向)水平剪力略有增大,无洞口方向(Y方向)水平剪力变化幅度很小。
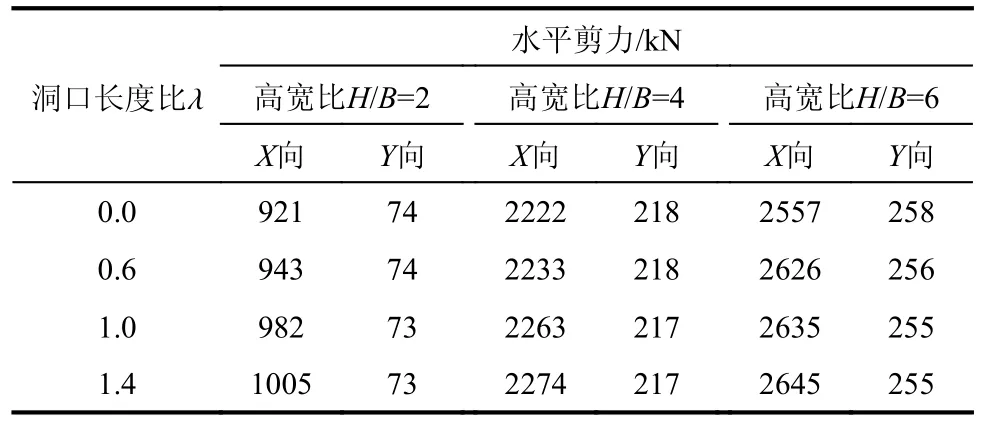
表17 非周边约束塔楼核心筒墙肢的水平剪力Table 17 Horizontal shear force of the shearwall of nonperipheral constraint tower
2)框架柱
在7 条地震波作用下,非周边约束塔楼框架柱KZ2(图1(a))首层水平剪力的变化情况见表18。由表18 可知,塔楼框架柱对周边是否有洞口非常敏感,框架柱在有洞口方向剪力显著减小,在无洞口方向剪力的变化幅度则很小。
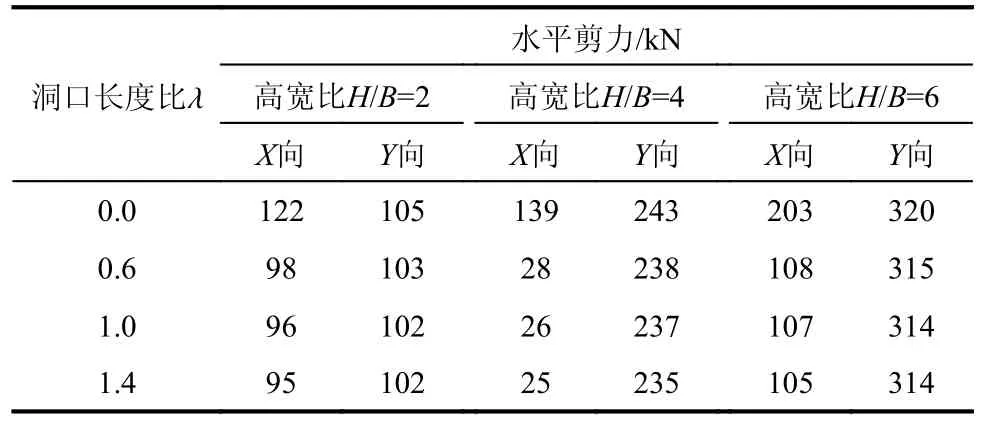
表18 非周边约束塔楼框架柱的水平剪力Table 18 Horizontal shear force of the column of nonperipheral constraint tower
在7 条地震波作用下,洞口周边框架柱KZ3(图1(a))地下1 层的水平剪力的变化情况见表19。由表19 可知,纯地下室部分的框架柱对楼板开洞非常敏感,当洞口长度比λ 为0.6 时,在有洞口方向框架柱剪力可增大数倍,在无洞口方向框架柱剪力的变化幅度很小。
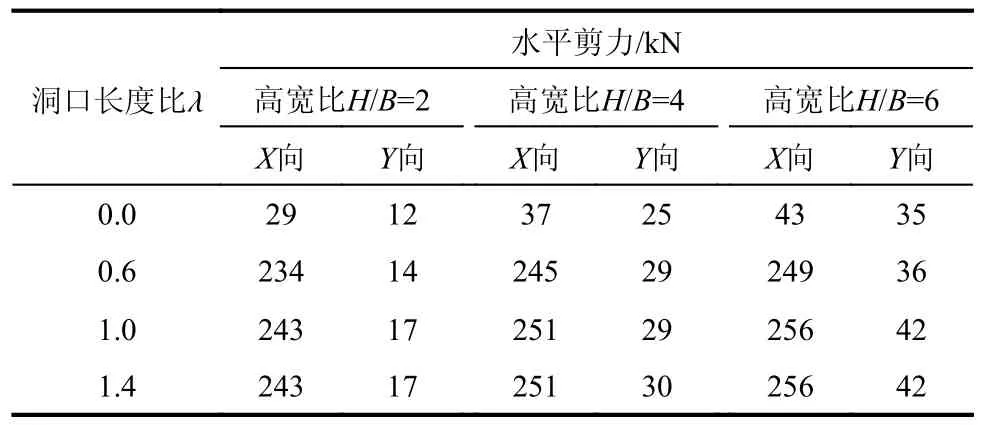
表19 洞口周边地下室框架柱的水平剪力Table 19 Horizontal shear force of the basement column around the opening
3)楼板
当H/B=4,且洞口长度比 λ=1.0 时,非周边约束塔楼在地震作用下,首层楼板正应力的分布如图10 所示。由图10 可知,在X方向地震作用下,在洞口上、下边缘以及塔楼背向洞口部位楼板正应力σXX显著增大;在Y方向地震作用下,楼板正应力σYY在洞口左、右边缘及洞口角部应力较大。随着洞口长度比λ 增大,首层楼板正应力逐渐增大;与首层楼板相比,其下各层楼板应力逐渐减小。
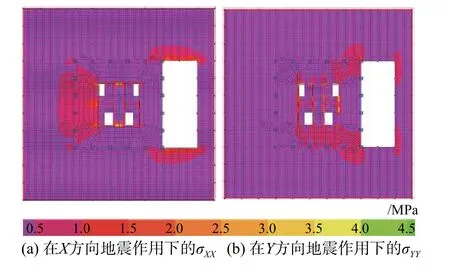
图10 地震作用下洞口长度比λ=1.0 时首层楼板的正应力Fig.10 Normal stress of first floor slab under earthquake action with opening length ratio λ=1.0
对于带有单边开敞地下室的塔楼,在地震作用下首层楼板正应力随塔楼高宽比和洞口长度比λ的变化情况如表20 所示。由表20 可知,在X方向与Y方向地震作用下,首层楼板最大正应力随洞口长度比λ 增大而显著增大。随着塔楼高宽比增大,首层楼板最大正应力略有加大。
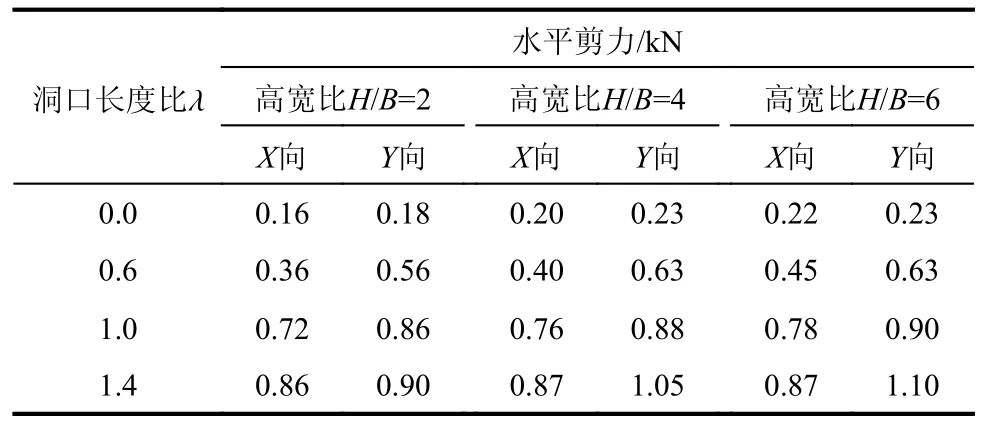
表20 非周边约束塔楼首层楼板的最大正应力Table 20 Maximum Normal Stress of First Floor of high-rise building without peripheral constraint
由此可见,塔楼非周边约束在技术上具有可行性。此时,需要对地下室楼盖、特别是地下室顶板进行加强,确保塔楼水平剪力向周边地下室可靠传递。
5 结论
基于塔楼、地下室与周边土体的相互作用机理,建立可以考虑地基基础影响的高层建筑力学模型,根据场地条件确定地下室周边土体弹簧及相应阻尼的计算参数。考察了结构在地下室顶板嵌固、地下室周边嵌固、底板嵌固以及土体-结构相互作用等4 类边界条件时地震作用下分析结果的合理性,并研究了塔楼单侧洞口长度对整体结构与结构构件受力性能的影响,得出以下结论:
(1)地下室顶板嵌固模型塔楼的侧向刚度最大,自振周期最短,在地震作用下塔楼的层间位移角最小,但无法考虑地下室与塔楼之间的相互影响。
(2)地下室周边嵌固模型地下室的水平位移受到强制约束,无法反映地下室结构的变形与质量引起的惯性力,在地震作用下地下室水平剪力沿竖向减小过快,计算结果偏于不安全。
(3)底板嵌固模型忽略地下室周边土体的作用,由于地下室的侧向刚度与质量均显著大于塔楼,导致地下室在地震作用下水平剪力过大,计算结果过于保守;
(4)土体-结构相互作用模型可以较为真实地模拟基础底部与周边土体的刚度与阻尼,结构自振周期加长,在地震作用下水平剪力减小,层间位移角增大,地下室水平剪力分布趋于合理。随着土体剪切波速提高,结构在运动方向受到的约束作用增强,地下室的水平剪力显著减小。
(5)在地震作用下,各种嵌固条件对剪力墙内力的影响较小,对框架柱内力的影响很大。采用弹簧与阻尼模拟地下室周边土体介质时,地下室框架柱的内力发生剧烈变化,其值可能远大于地面以上的框架柱。
(6)在地震作用下,地下室顶板弹簧反力最大;随着楼层深度增大,弹簧反力逐渐减小。随着土体介质剪切波速提高与塔楼高度增大,弹簧水平反力显著增大。
(7)塔楼单侧地下室洞口对结构动力特性的影响极小。在有洞口方向,塔楼层间位移角稍有增大,水平剪力略有减小;在无洞口方向,塔楼层间位移角与水平剪力基本保持不变。
(8)塔楼单侧地下室洞口对剪力墙内力影响较小,对框架柱内力和楼板应力影响显著。由此可见,当塔楼周边楼板设置大洞口时,需要采用准确的计算模型模拟地下室构件内力的变化,并采取相应的加强措施。

