基于屈曲模态的弹性压弯构件平面内二阶弯矩计算

范 浩，王 新，董卫国，温四清

(中信建筑设计研究总院有限公司，湖北，武汉 430014)

压弯构件在轴力和弯矩的共同作用下，其平面内弯矩由两部分组成[1]：一阶弯矩，它由外加荷载作用在结构变形前的空间坐标产生；二阶效应弯矩，它由轴力作用于杆件的侧向位移上产生，该侧向位移包含初弯曲和所有荷载(弯矩、剪力、轴力自身)产生的所有侧向变形(弯曲变形、剪切变形)。人们习惯将轴力作用于侧向位移产生的二阶效应弯矩分成两大类：构件两端无相对侧移时的P-δ 效应弯矩；构件两端有相对侧移时的P-Δ效应弯矩。

对于无侧移构件，诸多研究[1-8]都给出了精度很高的计算公式来估计P-δ 效应弯矩MII，其基本形式为：

式中：P为构件中的轴压力；Pcr,1为构件发生第一阶弹性屈曲时的轴压力(称为欧拉荷载)；βmx为各类荷载和边界条件下的等效弯矩系数(构件的实际最大二阶弯矩与均匀受弯构件的最大二阶弯矩的比值[1])；MI为构件中一阶弯矩最大值，这些研究成果也被我国新版钢结构设计标准采纳[9]。

对于规则框架结构中的有侧移构件(特指除框架本身外没有任何侧向支撑的构件)，一般引入一个二阶效应系数来计算同一层框架柱的P-Δ效应弯矩[3,10-11]，该系数实质就是轴力在一阶侧向变形上产生的二阶效应弯矩与水平力产生的一阶弯矩的比值。若要很好的估计有侧移框架柱在竖向荷载和水平力共同作用下的二阶效应弯矩MII，需要对无侧移变形弯矩和有侧移变形弯矩乘以不同的放大系数[12]：

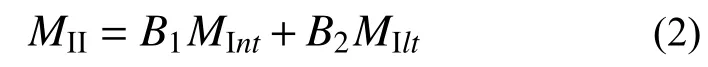
式中：MInt为假定框架没有侧移时按一阶弹性分析所得杆内弯矩；MIlt为按一阶弹性分析仅由框架侧移引起的杆内弯矩；B1为P-δ 弯矩放大系数(按无侧移情况对应的有效长度系数计算)；B2为P-Δ弯矩放大系数。由于B1会显著小于B2，倘若不加区分MInt和MIlt而将一阶分析得到的弯矩MI按照式(1)的形式采用统一放大系数B2计算有侧移框架压弯构件的二阶弯矩，则会得到过于保守的结果[13]。

对于弱支撑框架结构、空间结构、或者变截面构件或(和)变轴力构件，这些体系中的压弯构件均超出了传统构件设计方法——构件计算长度结合等效弯矩系数、弯矩放大系数设计方法的适用范围，结构工程师只能针对这类结构采用复杂的直接二阶分析方法[14]或是针对某类构件进行研究并引入诸多修正系数[15-16]以得到与传统方法形式(3)和式(4)一致的稳定设计公式[9]。

设计式(3)和式(4)中的系数φx(即柱子曲线)则经过了理论分析、构件试验和数值分析等各类研究方法的大规模验证，它全面考虑了构件初始缺陷和材料弹塑性的影响，该参数应该作为工程师设计一般压弯构件在平面内的稳定性的最基本最重要的依据。针对一般情形的压弯构件，如果能够找到简便、准确的方法计算出其二阶弯矩，则可以将设计式(3)和式(4)的适用范围推广至所有钢结构体系的压弯构件，从而避免了采用直接二阶分析方法时需要直接模拟真实初始缺陷或等效初始缺陷的繁琐和错漏[9,12,17]。

本文将针对一般钢结构体系中的压弯构件，不论其是否为规则框架、是否为有/无侧移构件，在不进行直接二阶分析的情况下，基于屈曲模态分析的方法，获取压弯构件的平面内二阶弯矩，然后可借助压弯构件稳定设计式(3)和式(4)进行构件设计。

1 基本方程

考察一个两端带有弹簧约束的等截面等轴力作用压弯构件[6,8,18]，如图1(a)所示，图1(b)为变形后的构件及其支座反力情况，图1(c)为构件的微元段隔离体。本文采用的如图1(c)下侧所示的空间直角坐标系x、y、z，相应方向的平动位移分别用u、v、w表示，基于右手法则，如图1(b)所示，转角、弯矩以逆时针为正，水平力、平动位移以坐标轴正方向为正，轴力则以受压为正。对图1(c)上侧的微元段隔离体进行平面内受力分析，建立x向和绕z轴的平衡方程(因等轴力假定故y向自动满足平衡条件)：

忽略高阶小量可得：

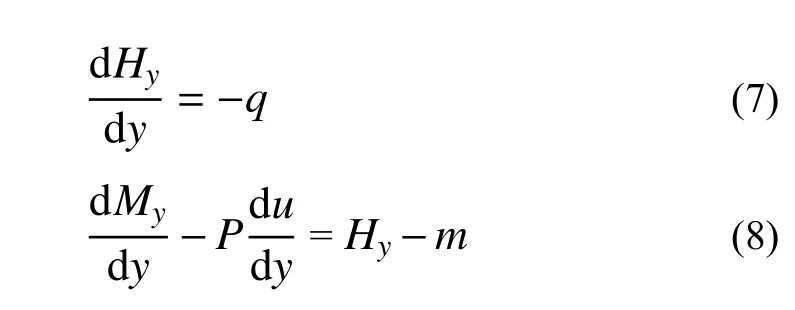
一般情况下，当图1 所示体系在跨内有集中水平力或集中弯矩作用时，可在集中荷载作用处分段，对每一段分别给出平衡方程式(7)和式(8)，在分段处应满足位移连续和力的平衡条件，最后联立各分段的平衡方程进行求解；本文为了保持形式上的简单和统一，使得后续的数学推导简单有效，采用均布荷载对集中荷载进行等效，等效方法如下：当跨中y处作用有集中水平力F0(或集中弯矩M0)时，用分布在极小区间[y-ε/2,y+ε/2]的均布线荷载q=F0/ε(或均布弯矩m=M0/ε 来替代。显然当区间宽度ε 趋近于0，上述等效方法分析得到的结果将收敛到集中荷载作用情形，因此，认为平衡方程式(7)～式(8)可用来描述等截面等轴力作用的压弯构件在平面内的任意受力状态。

图1 端部为弹性约束的压弯构件受力简图Fig.1 Force diagram of typical member under combined axial force and bending

2 屈曲模态求解

对式(8)再进行一次微分且令q=0和m=0(表示体系无横向外荷载作用)，根据小挠度假定且忽略剪切变形有My=-EIu′′，引入参数k2=P/EI，即可得到该体系的屈曲模态控制方程[6,8,18]：

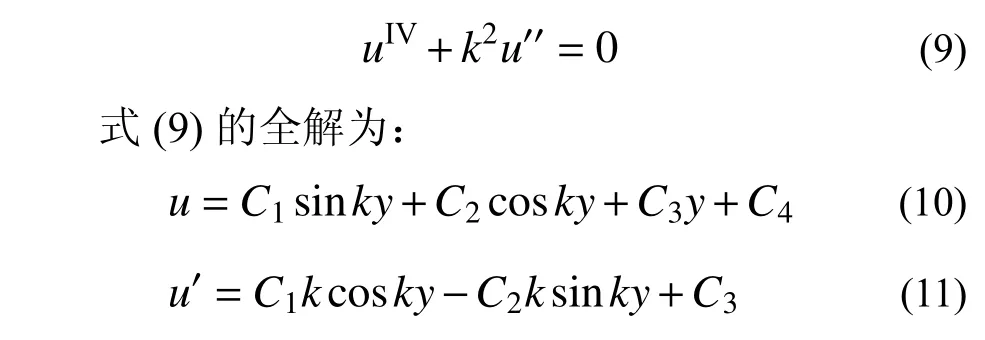
当式(10)中的常数均取为0 时，就是体系的零解，对应于原始直立的平衡状态。结合式(8)及式(10)～式(13)，可以得到水平力-PC3，求解式(10)中的k 及相应4 个常数C1～C4时，需要用到上、下端共4 个边界条件：

a)下端水平力，Hy(0)=-PC3=kAu(0)，若kA=+∞(下端无侧移)，u(0)=0；若kA=0(下端无侧向约束)，C3=0；

b)下端弯矩，My(0)=-EIu′′(0)=-rAu′(0)，若rA=+∞(下端无转动)，u′(0)=0；若rA=0(下端无转动约束)，u′′(0)=0；

c)上端水平力，Hy(l)=-PC3=-kBu(l)，若kB=+∞(上端无侧移)，u(l)=0；若kB=0(上端无侧向约束)，C3=0；

d)上端弯矩，My(l)=-EIu′′(l)=rBu′(l)，若rB=+∞(上端无转动)，u′(l)=0；若rB=0(下端无转动约束)，u′′(l)=0。

根据上述4 类边界条件可以组合出任意实际端部边界条件：铰接、固定、自由、弹性平动约束、弹性转动约束等。当构件是作为隔离体取自整体结构时，其边界约束的等效刚度值kA、kB、rA、rB是可以取负值的。由构件两端的边界条件可建立4 个线性方程，方程组存在非零解(即系数C1～C4不全为0)的条件就是其系数组成的4 阶行列式为0。由式(10)～式(13)可知，该4 阶行列式的唯一变量为k，展开后将得到一个包含三角函数的超越方程，由于三角函数的周期性质，k的解将有无穷多个。将其解按照由小到大依次排列，即可获得各阶模态的屈曲荷载然后代入原4 阶线性方程组，此时实际独立的方程只有3 个，因此，仅可确定第i阶屈曲模态的系数Ci1～Ci4之间的比值：Ci2/Ci1、Ci3/Ci1、Ci4/Ci1(此处假定Ci1为任意非零实数)，从而式(10)屈曲模态可以写成：

设ui、uj为体系的任意两个屈曲模态，其对应的屈曲荷载为ki和kj，满足0＜ki＜kj，可以证明体系的屈曲模态满足如下形式的正交性：

对式(16)左端第一项进行两次分部积分，并对左端第二项进行一次分部积分，整理得到：

令式(17)乘以截面的抗弯刚度EI，根据屈曲模态的通解表达式(10)～式(13)并利用水平力等式Hy=-PC3可得：

将式(16)中的屈曲模态ui、uj交换顺序，进行同样的处理可以得到：

由于ki＜kj，可证式(14)成立，从而式(15)也成立。

若体系受到的约束均为理想约束[19]，此时约束力在虚位移上所做的功恒等于零，也即约束既不储能也不耗能，如铰接、刚接、自由等，则有成立，此时式(15)可以简化写成：

在均匀轴压力P作用下的等截面理想直杆体系，如图1 所示，若其各阶屈曲模态已知，则体系的任意位移(竖向位移和侧向位移，不包含平动刚体位移)可以表示为：

相应的整个体系的势能Π 由外力势能V和内力势能U组成：

将式(23)代入式(24)～式(26)，并利用式(14)～式(15)的正交性，可得：

令总势能Π 的一阶偏导数均为0，即可得到图1 所示体系的平衡方程：

式(32)给出的是沿杆轴向的平衡关系式，式(33)给出的是保持原始理想直立状态的平凡解，式(34)给出的是屈曲模态的非平凡解，对比式(29)可知，取P=Pi即可。

3 构件的二阶效应求解

3.1 理论部分

第2 节针对图1 所示体系的屈曲模态控制方程、模态解的形式、边界条件、方程求解、模态的正交性以及屈曲模态的稳定性进行了较为全面的讨论，下面将对构件平面内二阶效应进行探讨，与已有文献方法[1,6,8]不同，本节将系统介绍采用屈曲模态分解的求解方法。

将式(8)进行整理可得：

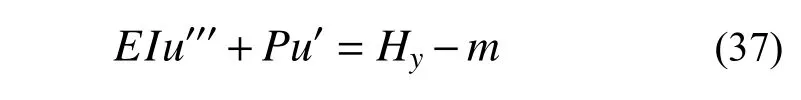
令u=u0+uI+Δu，其中u0、uI、u、Δu分别为初始缺陷、外荷载引发的一阶分析位移、二阶分析位移和二阶效应产生的位移增量，代入式(37)整理可得：

式(38)中水平力Hy来源包括横向外荷载和二阶倾覆效应产生的水平力ΔHy，令P=0，即得到相应的一阶分析平衡方程：

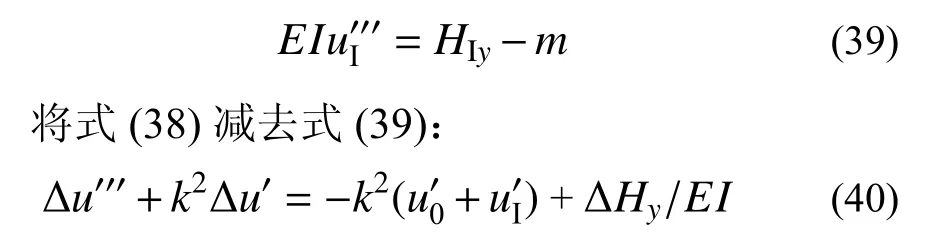
式(40)建立起了Δu与u0和uI的关系，可见u0与uI对于体系的作用几乎是一致的(不同点在于，初始缺陷u0在一阶分析时不会产生内力)，二阶效应均与它们的一阶导数相关。

对式(40)再进行一次微分，则可得到：

式(41)与相应的屈曲模态控制方程式(9)的等号左端形式完全相同，显然，对于同一体系而言，式(41)的解与式(9)的解都应满足相同的边界条件。

利用屈曲模态一阶导数的正交性，可将一阶分析位移uI(或初始缺陷u0)的一阶导数唯一的分解成体系屈曲模态相应导数的形式：

当体系的约束满足理想约束的条件时，屈曲模态的二阶导数也满足式(22)的正交关系，因此，一阶分析位移uI(或初始缺陷u0)的二阶导数也可唯一的分解成体系屈曲模态二阶导数的形式：

求解式(41)时，u0与uI在数学上完全等价，为方便描述问题，现令u0≡0，将式(42)代入式(41)：

对式(53)进行两次积分，得到二阶效应侧移增量的原函数表达式：

将体系上、下端共4 个边界条件代入式(54)即可确定未知系数A、B、C、D，显然体系各阶屈曲模态及其线性组合均能满足体系的边界条件，因此，式(54)满足体系边界条件等价下式满足边界条件：

式(55)与体系的屈曲模态解式(10)的形式完全一致，若式(55)存在非零解，由于k的任意性，则意味着任意轴力值P都是体系的屈曲荷载，这显然是不可能的。因此，必然有Δug≡0。从而式(50)的全解为：

若令式(41)中uI≡0，且将式(42)和式(43)中的uI替换成u0，则式(56)和式(57)也是有任意初始缺陷u0的二阶效应级数解，所不同的是，由于初始缺陷u0本身对应的一阶弯矩为0，故由初始几何缺陷u0导致的二阶弯矩可以表示为：

3.2 常见体系二阶效应求解

本节采用屈曲模态方法对两种典型体系的常见荷载工况求解其平面内二阶弯矩。

3.2.1 两端铰接无侧移体系

图2 给出了一定轴压力作用下体系的一阶弯矩、二阶弯矩的精确解[6]以及二阶弯矩的级数解。结果对比表明：对于均布荷载和跨中集中荷载作用情况，级数解与精确解高度重合，但对于杆端存在弯矩情况，级数解的收敛速度明显变慢，且在端部位置存在震荡与突变，这是因为对于两端铰接体系来说，各阶屈曲模态对应的端部弯矩为0，而相应的一阶弯矩在端部非0，导致级数解在该端部无法收敛。

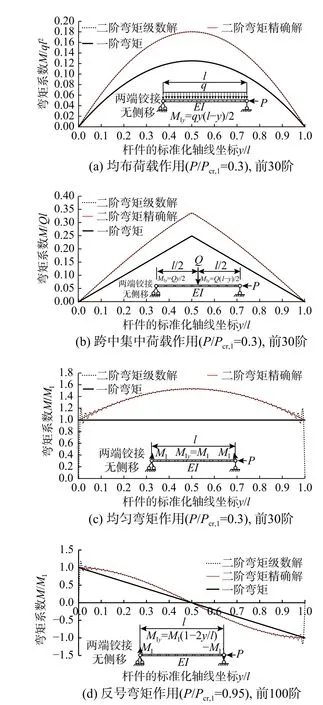
图2 两端铰接无侧移体系的二阶弯矩计算结果Fig.2 Second-order in-plane moment of pinned end system by buckling model method

3.2.2 两端无转动有侧移体系

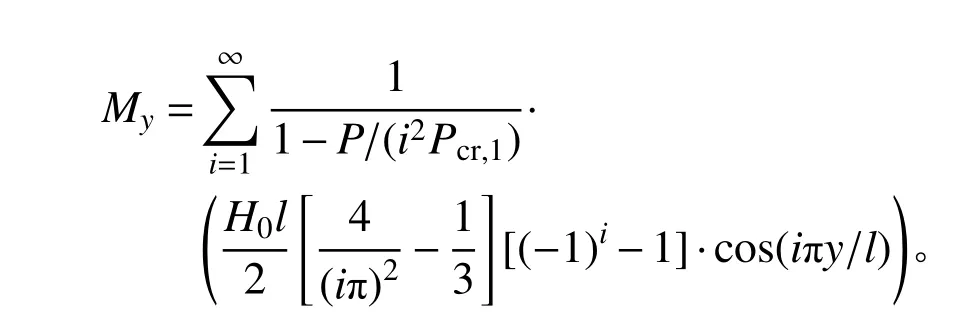
该类情形的二阶位移和二阶弯矩的精确理论解为：

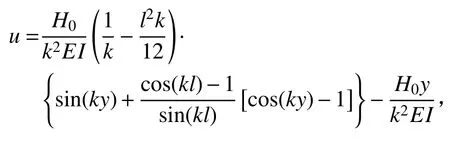
上述两个算例表明：尽管其一阶弯矩结果完全相同，但是屈曲模态分解法给出的二阶弯矩放大系数完全不一样。事实上从式(8)来看，二阶效应来源于构件轴力与其侧移一阶导数的乘积，而与一阶弯矩本身并无直接关系。用一个极端的例子来说明：任意等截面理想直杆，在均匀轴力、相同端弯矩和沿构件截面高度的梯度温度作用下，当端弯矩产生的构件曲率与梯度温度产生的构件曲率大小相等符号相反时，其一阶分析结果是该构件处于均匀受弯状态但无任何变形，此理想构件的二阶效应为0，即其二阶分析结果与一阶分析结果完全一致。

针对上述两种情况，图3 给出了一定轴压力作用下体系的一阶弯矩、二阶弯矩的精确解以及二阶弯矩的级数解。结果对比表明：对于支座无转动变形的有侧移情况，级数解与精确解高度吻合，但对于杆端存在初始转角而无侧移的情况，级数解一直在精确解附近震荡，并且越靠近构件端部震荡越剧烈，最终在端部发散，这是由于后者出现了支座转动位移，而体系的各阶屈曲模态端部则严格保持零转角。

图3 两端固接有侧移体系的二阶弯矩计算结果Fig.3 Second-order in-plane moment of fixed end with lateral displacement system by buckling model method

从前述算例和级数解的叠加原理可知，当无约束的自由度作用外荷载时，或是完全约束的自由度出现支座位移时，与精确理论解相比，级数解均存在不小的瑕疵，在极端情况下无法得到具有足够精度的解甚至出现发散的情况；而其余情况下，级数解的精度虽然足够，但计算量极大。上述情况严重限制了级数解在实际工程中的应用，下文试图寻找一种可兼顾精度和效率的处理方法。

4 屈曲荷载的分布规律

式(58)表明：各阶模态的二阶效应放大系数为1/(1-P/Pcr,i)，它会随着阶数增加而减小，并逐渐趋近于1.0。如果仅对第一阶屈曲模态的二阶效应进行精确计算，而对高阶屈曲模态采用统一的放大系数来估计，如若不带来较大的误差，则可得到效率和精度兼顾的级数解的近似解。

为了解高阶模态二阶效应放大系数的分布规律，本节将对图1 所示体系进行参数分析。考虑的参数包含无侧移情况(kA=kB=+∞)、有侧移情况(kA=+∞且kB=0)、上端转动约束情况(rA=αEI/l)、下端转动约束情况(rB=βEI/l)，α、β 的取值包含0.0、0.1、1.0、10.0、+∞五种情况(上述参数涵盖了所有的等效计算长度情形)，分别用α1～α5和β1～β5表示。

采用Midas Gen 2016 对图1 进行有限元建模，不考虑构件的剪切变形，进行特征值屈曲分析，得到的结果如图4～图5 所示。图4 给出的是各阶屈曲荷载与前一阶屈曲荷载比值，随着端部约束刚度的增加，该比值逐渐减小，端部约束对Pcr,2/Pcr,1的影响巨大，但是随着阶数增加，端部约束对高阶屈曲模态的Pcr,i+1/Pcr,i的影响越来越小，其比值逐渐均匀的趋近于(i+1)2/i2。图5 给出的是各阶屈曲荷载与第一阶屈曲荷载的比值，显然Pcr,2/Pcr,1最小，随着阶数的增加，Pcr,i+1/Pcr,1均迅速增加，端部约束刚度越大，该比值增加越慢；两端固定无侧移体系的Pcr,i+1/Pcr,1取最小值，依次为2.0、4.0、6.0、9.0、12.0、16.0、···、+∞。

图4 轴心受压构件各阶屈曲荷载与前一阶屈曲荷载比值(Pcr,i+1/Pcr,i)的分布规律Fig.4 Pcr,i+1/Pcr,i distribution of axial compression member

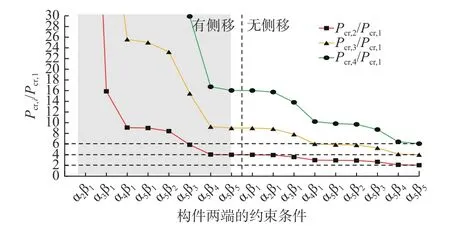
图5 轴心受压构件各阶屈曲荷载与第一阶荷载比值(Pcr,i+1/Pcr,1)的分布规律Fig.5 Pcr,i+1/Pcr,1 distribution of axial compression member

5 平面内二阶弯矩估计

第4 节的参数分析表明：Pcr,i/Pcr,1会随着模态阶数迅速增加，且不小于2.0、4.0、6.0、9.0、12.0、16.0、···、+∞，因而当2≤i＜j时，有：

式(61)和式(62)仅对第一阶屈曲模态弯矩的二阶效应进行了准确的计算，而对高阶模态弯矩部分则采用了统一的放大系数进行估算，因此误差来源于高阶模态弯矩的二阶效应。采用式(61)和式(62)对3.2 节中讨论的6 种情况进行验证，得到的计算结果如图6 和图7 所示。当第一阶屈曲模态弯矩占据主导地位时，如图6 (a)～图6(c)和图7(a)所示，式(62)的结果与精确解几乎完全重合；当第一阶屈曲模态弯矩为0(如图6(d))或第一阶屈曲模态弯矩没有占据主导地位时(如图7 (b))，精确解落在式(61)和式(62)之间或附近，在估计二阶弯矩的最大值方面，式(62)仍然给出了非常精确的结果，而式(61)则给出了相对偏大的估计结果。

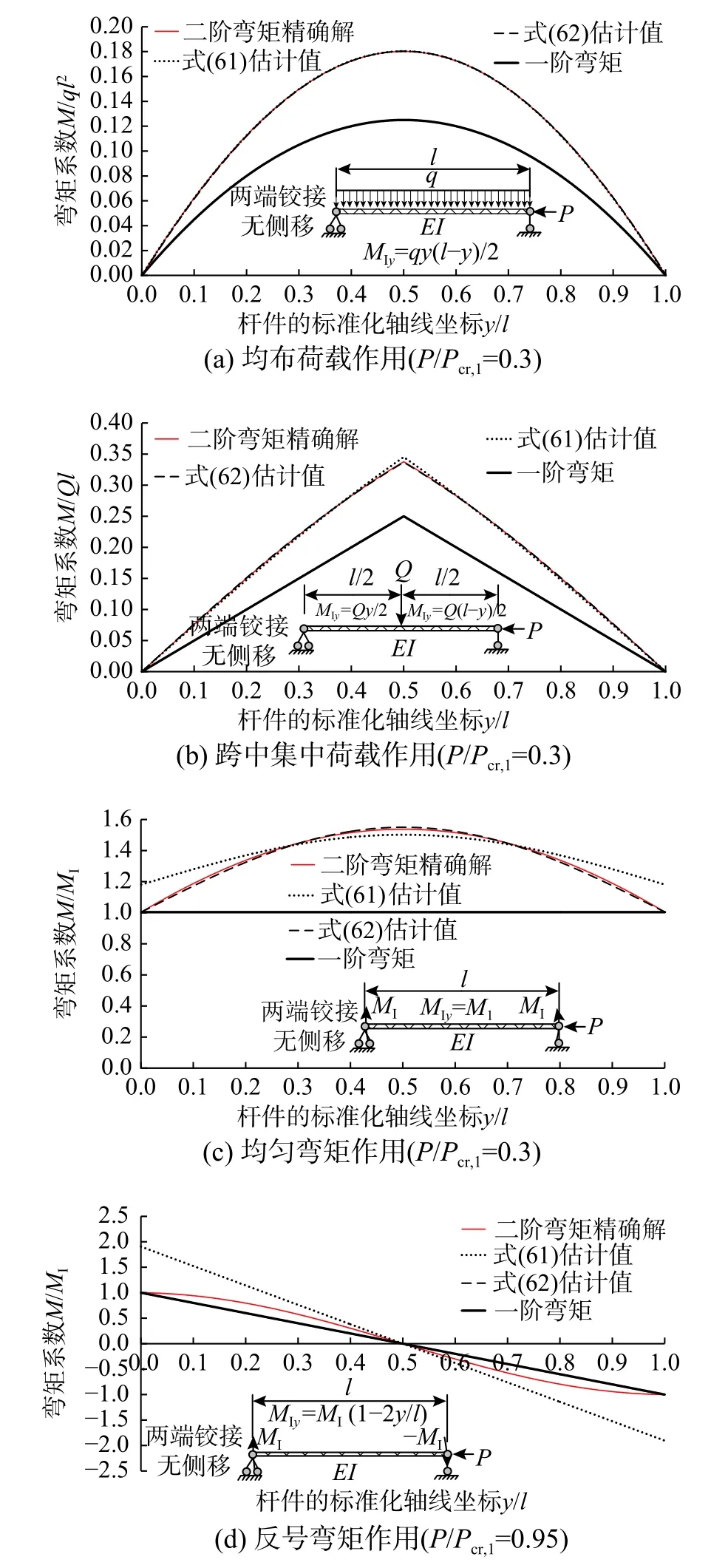
图6 两端铰接无侧移体系的二阶弯矩估计结果Fig.6 Etismation of Second-order in-plane moment of pinned end system

图7 两端固接有侧移体系的二阶弯矩估计结果Fig.7 Etismation of Second-order in-plane moment of fixed end with lateral displacement system

式(61)和式(62)仅需利用构件的第一阶屈曲轴力、第一阶屈曲模态和一阶分析的弯矩结果，就可以对其二阶弯矩(由外荷载产生，不含初弯曲、初始偏心的影响)进行估计，完全克服了式(58)弯矩求解的计算繁复和结果发散的问题。而与传统方法相比，求解过程不再需要知道构件是否有无侧移、不再需要区分竖向荷载产生的弯矩和水平力产生的弯矩。

尽管前述少数典型算例表明式(62)具有足够的估值精度，然而其对高阶模态弯矩会存在偏小估值误差，如若体系仅作用第二阶模态弯矩时，最大低估误差为：

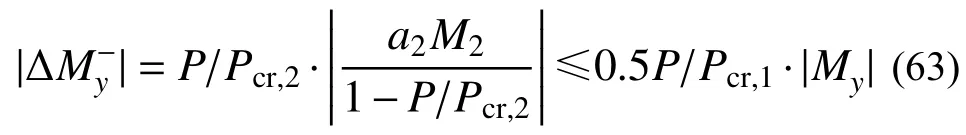
式(63)表明：体系承受的轴力越大，式(62)的估值误差越大，右侧不等式的等号对应于两端固接无侧移体系，当P/Pcr,1=0.3时，式(62)会存在15%的估值误差。

相应地，式(61)则对高阶模态弯矩可能会存在偏大估值误差，若某体系的第k阶屈曲荷载满足Pcr,k/Pcr,1=γ≥2.0，当该体系仅作用第k阶模态弯矩时，相应地高估误差达为：

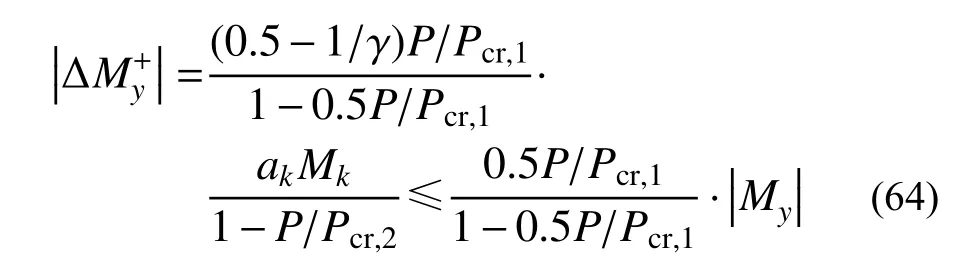
式(64)表明：体系承受的轴力越大，式(61)的估值误差越大，右侧不等式的等号对应于γ 趋近于无穷大的情形，当P/Pcr,1=0.3时，式(61)会存在17.6%的估值误差。

上述极端情形的误差分析表明：仅采用式(62)进行估值会出现偏不安全的情况，而式(61)也会有估值过高的情形，综合考虑，本文建议采用如下公式计算构件的二阶弯矩：

式(66)实际上接近于式(61)和式(62)两个界限值的中间值。当式(65)和式(66)给出两个估算值同号或构件截面对称，则取二者的较大绝对值；当构件截面不对称且二者异号时，应将两个计算结果分别进行承载力验算。

采用式(65)和式(66)式进行二阶弯矩估计时，与式(63)和式(64)式相应的估值误差可以改写为：

利用式(65)和式(66)估计二阶弯矩进行构件设计时，由于弯矩计算存在误差ΔMy，相应的设计应力比：

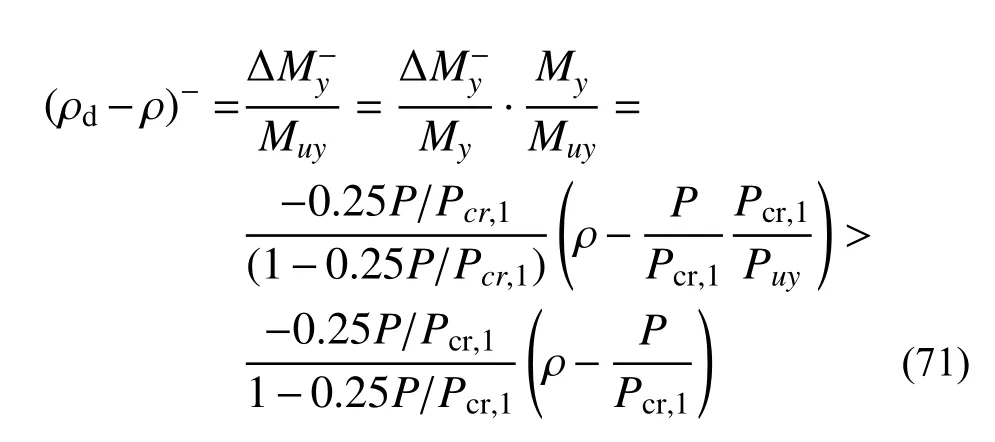
式(70)和式(71)表明：利用式(65)和式(66)进行构件稳定承载力验算时，其最大应力比误差可以用P/Pcr,1和ρ 来估计。图8 给出了式(70)和式(71)不等号最右侧部分的图像，可见应力比误差为构件真实应力比ρ≤1.0 的增函数，对于任意给定的ρ，应力比误差曲线接近于关于P/Pcr,1的抛物线，其两个零点分别为P/Pcr,1=ρ(轴心受压状态)和P/Pcr,1=0(纯受弯状态)，且最大高估误差与最大低估误差是对称的。采用式(65)和式(66)计算构件的二阶弯矩并对其平面内稳定进行验算时，当应力比按0.9 控制时，应力比误差不会超过0.06；当P/Pcr,1不超过0.3 时，应力比误差也不会超过0.05。

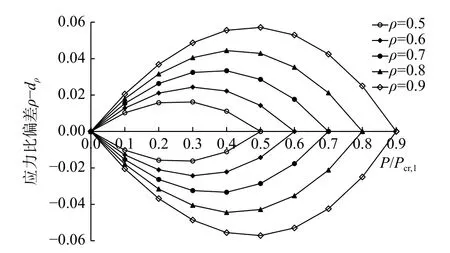
图8 应力比误差ρd-ρ 与P/Pcr,1和ρ 的关系Fig.8 Error ρd-ρ affected byP/Pcr,1 and ρ

6 第一阶模态系数最大值

7 与有限元法结合

接下来讨论基于前述方法并借助有限元单元法的一阶分析结果和屈曲模态分析结果计算构件的平面内二阶弯矩。以三阶纯弯梁单元为例，其单元的弯曲变形曲线用三次抛物线来描述：

由单元两端的几何边界条件u(0)=δ1，u′(0)=-δ2，u(l)=δ3，u′(l)=-δ4，得到u=A{δ}，u′=C{δ}，式中{δ}=[ δ1δ2δ3δ4]T，对于同一单元的两个侧向变形的一阶导数的积求定积分，有：

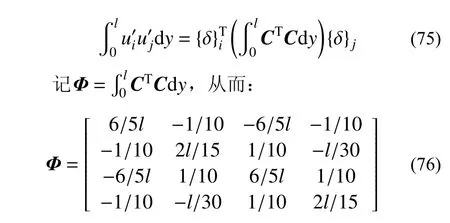
式(76)即为单元的几何刚度矩阵[6]，结合式(75)和式(76)可知，采用有限元方法计算式(43)中的a1仅需对节点位移进行标量计算即可：

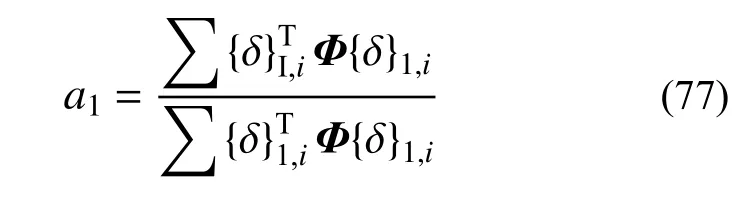
由a1M1,i=-a1EI(A)′′{δ}1,i计算第i个单元的第1 阶屈曲模态弯矩，其中：

在有限元分析程序中，可以直接利用单元刚度矩阵得到节点弯矩，然后线性插值得到单元内部的第一阶模态弯矩，再利用式(65)和式(66)即可求得相应的平面内二阶弯矩。

如图9(a)所示，采用Midas Gen 对第3.2.1 节的两端铰接无侧移体系建立有限元模型，柱截面H400×250×10×12，强轴定义为平面内，平面内抗弯刚度EI=5.57×107N·m2，约束弱轴方向平动自由度，柱高l=10 m，分成10 个单元，柱顶施加轴压力进行屈曲分析得到第一阶屈曲模态为图9(b)所示(左为平动位移，右为转角位移，余同；需要指出的是，Midas Gen 软件的转角位移为顺时针为正，与本文定义相反)，施加全跨作用均布荷载q=1 kN/m、跨中作用集中荷载Q=10 kN、两端作用同号相等弯矩MI=1 kN·m、两端作用异号相等弯矩MI=1 kN·m 进行一阶分析，得到的位移结果如图9(c)～图9(f)所示。

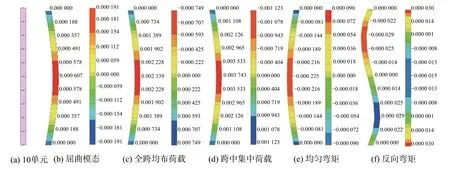
图9 有限元分析算例Fig.9 A calculation example by finite element analysis

采用本节方法分析得到二阶弯矩与相应的精确解详图10，与图6 相比，本节方法可以得到精度较高的构件平面内二阶弯矩，由于需要对分段插值函数求二阶导，本节方法得到的结果并不连续(提取结果时相邻节点的结果取较大值)和光滑。

图10 两端铰接无侧移体系基于有限元方法的二阶弯矩估计结果Fig.10 Estimation of Second-order in-plane moment of pinned end system by finite element method

8 结论

本文对一般约束条件下的等截面等轴力线弹性压弯构件在弯矩作用平面内的屈曲模态和二阶弯矩的屈曲模态级数解进行了深入探讨，可以得到以下结论：

(1)构件屈曲模态的一阶导数和二阶导数满足正交关系，构件的任意平动位移的一阶导数可以唯一的分解成用其屈曲模态一阶导数的级数和形式；

(2)基于小挠度假设和体系的势能极值和驻值情况，严格论证了体系各类平衡状态的稳定性：当P＜P1时，体系的直立平衡态是稳定平衡的；当P＞P1时，体系的直立平衡态和高阶屈曲模态均为不稳定平衡状态；当P=P1时，体系的第一阶屈曲模态是一种随遇平衡状态；

(3)采用屈曲模态分解的方法，将体系的二阶弯矩表示成其屈曲模态的级数和形式，各阶屈曲模态对应的弯矩放大系数是其相应屈曲荷载的函数，对几种常见的情形进行了算例分析；

(4)不同约束条件下，各阶屈曲荷载与第一阶屈服荷载的比值，随着阶数的增加，Pcr,i/Pcr,1均迅速增加，端部转动约束刚度越大，该比值增加越慢；当两端完全固定时，Pcr,i/Pcr,1取最小值，依次为2.0、4.0、6.0、9.0、12.0、16.0、···；

(5)结合二阶弯矩的屈曲模态级数解形式和屈曲荷载的分布规律，给出了二阶弯矩估算方法，该方法仅需已知构件的第一阶屈曲轴力、第一阶屈曲模态和一阶分析的弯矩(由外荷载产生，不含初弯曲、初始偏心的影响)，对几种常见情形进行了算例计算与误差对比，并对极端情形下的误差进行了分析；

(6)对第一阶模态弯矩系数和第一阶模态位移系数的最大值进行了推导，明确了二者取极值的条件，算例表明，该值最大为4/π；

(7)基于有限元分析结果，给出了采用屈曲模态分解法计算二阶弯矩的方法。