二维泊松方程问题Lagrange 型有限元p 型超收敛算法

叶康生，孟令宁

(清华大学土木工程系，土木工程安全与耐久教育部重点实验室，北京 100084)

有限元法[1]自诞生至今已经经历了长足的发展并在科学和工程领域得到了广泛的应用，目前已经成为结构工程领域最主要的分析计算方法。该法的解答精度主要依赖于网格和单元次数，为提高精度，常规有限元需要加密网格或提高单元次数，致使自由度快速增加，使得计算成本急剧提高，这在多维问题中尤为显著。为兼顾有限元法的效率和精度，国内外学者在天然超收敛性的基础上对超收敛后处理进行了大量研究，如Zienkiewicz 和Zhu 的SPR 法[2-3]、Wiberg 的SPRD法[4]、Boroomand 和Zienkiewicz 的REP 法[5]、Ubertini 的RCP 法[6]、Payen 和Bathe 的NPF-based 法[7]及SIP 法[8-9]、袁驷的EEP 法[10-12]等。这些方法中，以SPR 法的影响最大，该法具有计算简便，适用性广等优点，但其实施依赖于应力超收敛点，对于没有应力超收敛点的单元则难于实施。其他各类方法亦各有局限，研究更加通用、可靠的超收敛后处理方法仍有重要的理论意义和工程应用价值。

Douglas 和Dupont[13]对二阶常微分方程两点边值问题，提出了一种基于单元结点位移超收敛性，在单元内使用更高次基函数近似求解控制方程的超收敛算法。本课题组将该思想拓展应用至杆件自由振动问题[14]、平面曲梁和旋转壳静力问题[15-16]、平面曲梁和旋转壳自由振动问题[17]、一维非线性常微分方程及常微分方程组问题[18]及一维自适应分析[19]中。以上问题均为常微分方程问题，力学中还有大量二维问题，如板、壳的弯曲，弹性力学平面问题等，这些问题往往归结为求解偏微分方程边值问题。本文进一步将该思想拓展应用至这类问题的有限元超收敛计算中。由于偏微分方程边值问题亦有不同种类，为简单起见，本文以二维泊松方程问题为模型问题探讨二维C0型问题有限元的超收敛求解。C0型有限元亦分若干种类，本文仅限探讨双向同次的Lagrange型单元，这类单元具有很好的抗畸变能力[20]和解答性态。对于其他类型的单元，将另文探讨。

1 模型问题及有限元分析

二维泊松方程是典型的椭圆型偏微分方程边值问题，科学和工程中的弹性薄膜问题、渗流问题、静电场问题、自由扭转等问题均可由此方程描述。

本文对此方程的有限元超收敛计算开展研究，并以薄膜问题为模型进行论述，方程具体为：

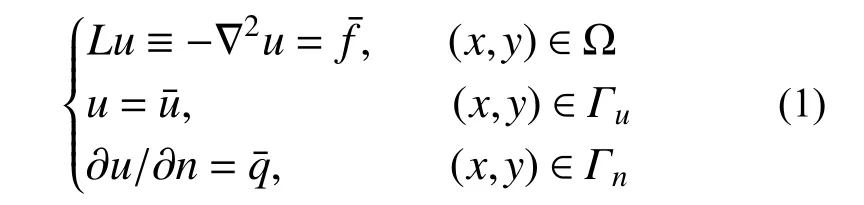
式中：u(x,y)为待求位移；n为边界外法线方向；Ω为求解域，∂Ω 为 Ω的边界，∂Ω=Γu∪Γn，Γu∩Γn=Ø，Γu和 Γn分别为固定边界和自由边界，分别给定Dirichlet 和Neumann 边界条件。该问题对应的能量泛函为：

式中，()x=∂()/∂x,()y=∂()/∂y。

对二维求解域通过网格划分进行单元离散，以矩形网格剖分为例，如图1 所示。记x向、y向网格划分分别为：

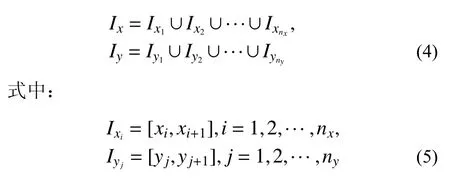
图1 有限元网格Fig.1 FE mesh

则二维有限元网格划分可简单表示为：I=Ix×Iy。该划分将求解域离散为ne=nx×ny个矩形单元。将网格结点集记为Zh，它包含结点(xi,yj)，i=1,2,···,nx+1,j=1,2,···,ny+1。单元尺寸he为单元(e)的最大边长，网格尺寸为所有单元边长的最大值，即：

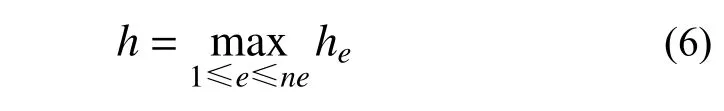
在该网格下，采用双向m次Lagrange 单元对该问题进行求解，将单元(e)上的真解近似为双向m次Lagrange 多项式：

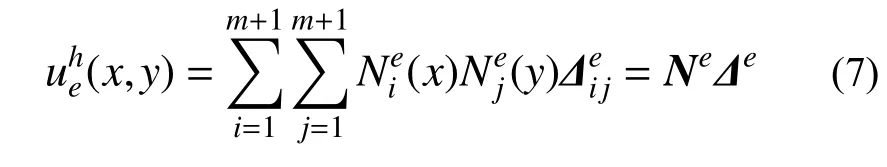
式中：Ne为单元形函数矩阵；Δe为单元的结点自由度向量。

相应地，全域解近似为：

式中：Nr(x),r=1,2,···,mnx+1为x向网格Ix上的整体m次形函数；Ns(y),s=1,2,···,mny+1为y向网格Iy上的整体m次形函数；Δh为整体的结点自由度向量。

将式(8)代入式(2)，将整体能量泛函离散为：

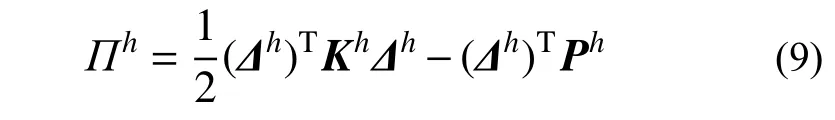
式中：Kh为整体刚度矩阵；Ph为整体的结点荷载向量。表达式如下：

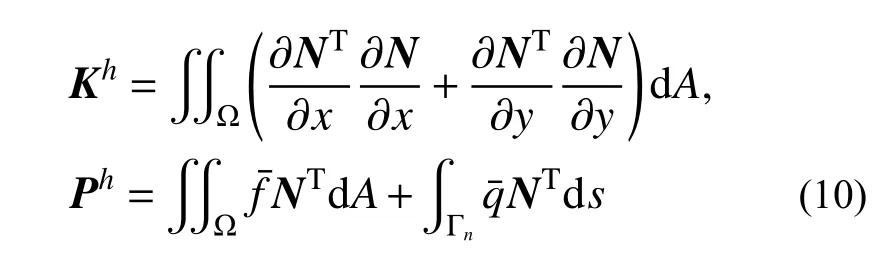
对该泛函引入固定边界Γu上Dirichlet 边界条件后取极值，并将边界条件处理后的整体刚度矩阵和结点荷载向量仍记为Kh和Ph，则可得有限元方程：

由该方程可求得 Δh，代入式(8)可得有限元位移解uh。记有限元解误差为：

其x向、y向导数误差分别为：

定义有限元导数误差为：

该有限元解答具有如下收敛性[1]：

通常情况下，双m次矩形元域内的网格结点集 Zh上位移解具有如下超收敛性质[21]：

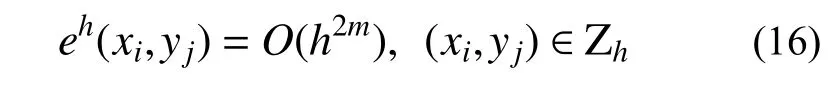
对一般四边形网格，网格结点位移不一定具有上述h2m阶的超收敛性质。文献[22]指出，参数变换为强正规的，即满足单元接近平行四边形，对边弯曲程度相近以及单元过渡时边的方向角改变量为高阶小量等条件，则四边形等参元在网格结点上仍具有超收敛性质。而在一般边界条件下，边界层(边界附近的1 层～3 层单元)网格结点解答的精度往往较差甚至丧失超收敛性。

网格结点位移解的超收敛性是本文建立p型超收敛算法的基础。

2 超收敛求解思路及误差估计

上述有限元求解过程可等效为如下的两步逐维离散过程：先采用有限元线法[23](以下简称线法)进行一维离散(沿x向在Ix网格上作m次元离散)，再对线法控制方程进行一维离散(沿y向在Iy网格上作m次元离散)。

线法网格如图2 所示，记(el),e=1,2,···,nx为线法单元，Lm(e-1)+2,Lm(e-1)+3,···,Lm(e-1)+m为(el)内部结线；Lm(i-1)+1,i=1,2,···,nx+1为x=xi处网格结线，dr(y),r=1,2,···,mnx+1为结线位移函数。

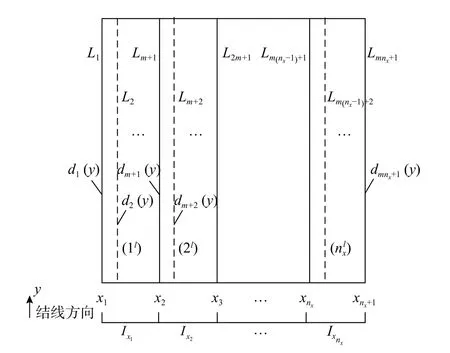
图2 有限元线法网格Fig.2 FEMOL mesh

线法将全域解近似为：

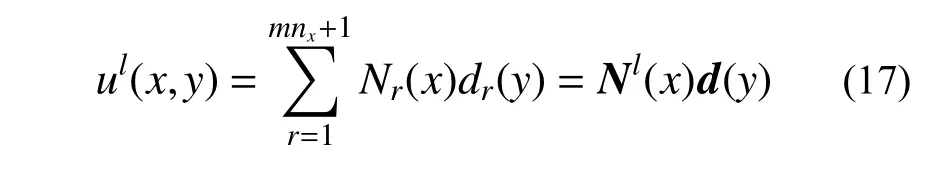
式中：Nl(x)为线法整体形函数矩阵；d(y)为结线位移向量。

对式(17)引入固定边界 Γu上的位移条件，并代入式(2)中能量泛函，通过泛函取极值，可得线法控制方程：

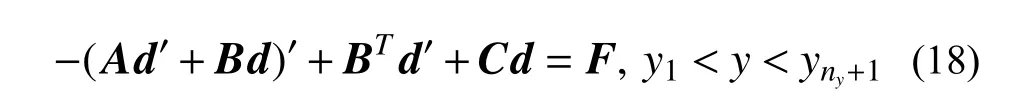
式中：()′=d()/dy；A、B、C、F均为y的函数。其表达式及方程的边界条件可参见文[23]。

上述线法控制方程为常微分方程边值问题，对该问题进行一维有限元离散(沿y向在Iy网格上作m次元离散)，将结线位移离散为：

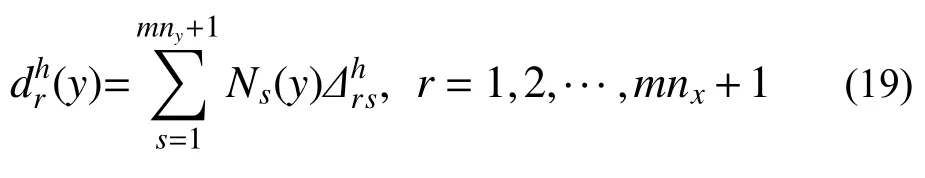
如此经两步逐维离散过程后的位移表达式为：

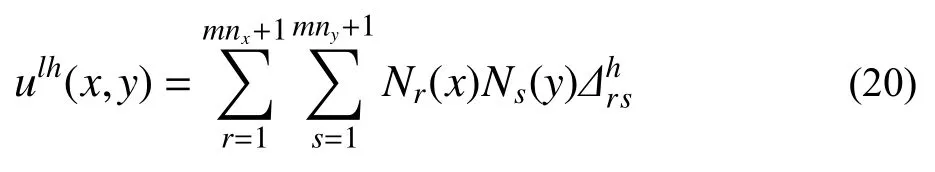
易见矩形网格分两步逐维离散与直接进行二维Lagrange 单元离散可得到相同的离散格式，两者代入泛函取极值可得到相同的控制方程及解答，故式(20)与式(8)中的相同，未作区分。并有如下等效关系：

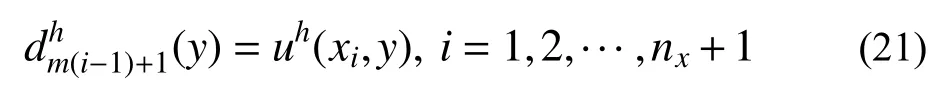
因第二步离散仍为一维有限元过程，则由文献[1]可得，结线上网格结点解有如下超收敛性质：

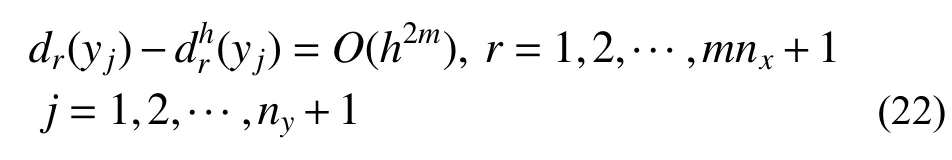
而对于x=xi,1≤i≤nx+1处网格结线Lm(i-1)+1上的网格结点，由式(16)、式(21)、式(22)可得如下估计式：

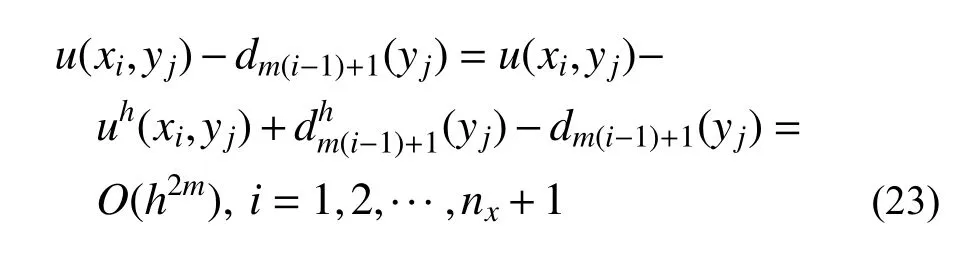
由于求解线法控制方程时，y向网格可任意布置，故区间[y1,yny+1]中任一点均可设为网格结点，故有：

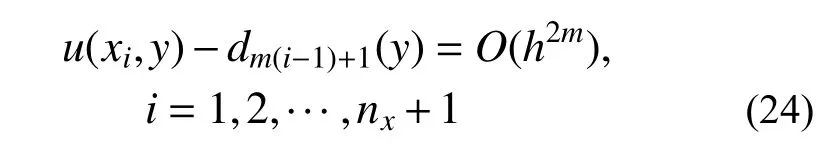
即线法网格结线上的解答具有h2m阶的超收敛性质。

为提高二维有限元单元y向边界解答的精度和收敛阶，本文基于式(22)中结线上网格结点解的超收敛性，对线法控制方程采用p型超收敛进行修复，过程如下：

线法控制方程在y向网格上的真解d，应满足如下表达：

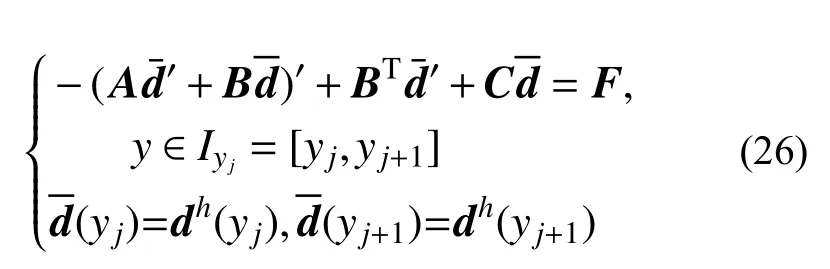
上述p型超收敛过程等效于对二维网格划分中的第j行子域采用次单元进行有限元求解，其中在边界取为原有限元解，其余边界与原边界条件一致，如图3 所示。Ix×Iyjm×y=yj,y=yj+1

图3 单元y 向边位移恢复(m=2,=3)Fig.3 Recovery of displacements on y-direction edges of elements(m=2,=3)

依次取所有ny个行子域Ix×Iyj,j=1,2,···,ny，即可求得所有单元y向边界的超收敛解u*(xi,y),i=1,2,···,nx+1,y∈Iy。

同理，亦可将上述逐维离散过程视为先对y向进行线法离散，后对线法控制方程在x向进行一维有限元离散。类似地，对第i列子域Ixi×Iy,i=1,2,···,nx采用×m次单元对原泊松方程问题进行有限元求解，其中在x=xi,x=xi+1边界取为原有限元解，其余边界与原边界条件一致，如图4所示。可得所有单元x向边界的超收敛解u*(x,yj),j=1,2,···ny+1,x∈Ix，且有：

图4 单元x 向边位移恢复(m=2,=3)Fig.4 Recovery of displacements on x-direction edges of elements (m=2,=3)

在求得全部单元边界(网格线)上的超收敛解后，取出二维网格划分中的单元域1,2,···,nx,j=1,2,···,ny，采用双次单元进行二维有限元求解，其边界解取为前述边界超收敛解，如图5 所示，即用：

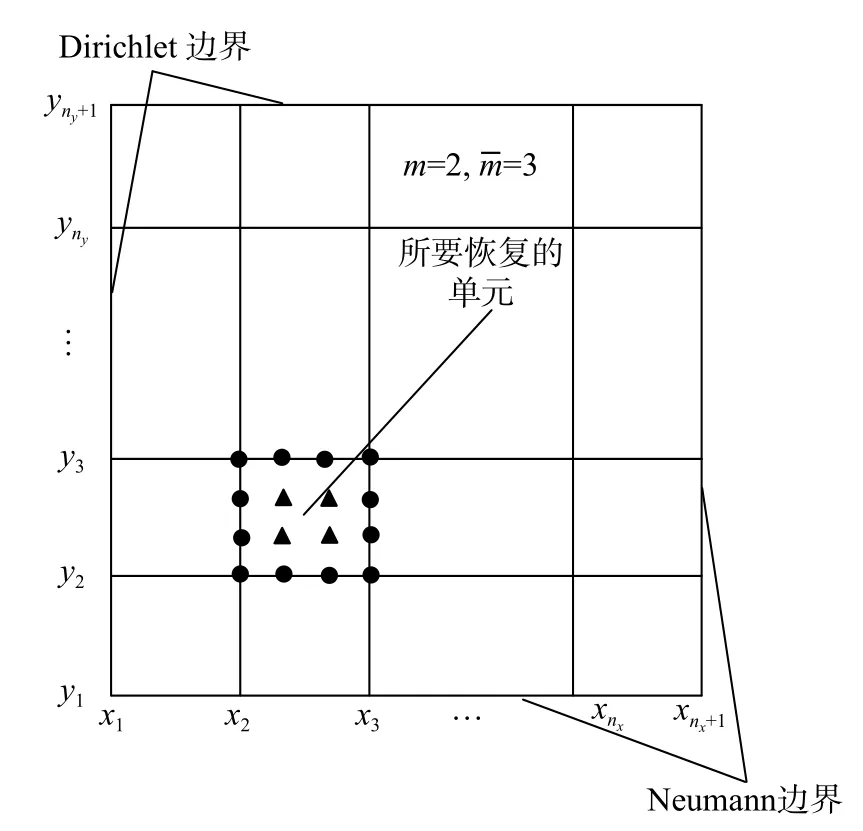
图5 单元域位移恢复(m=2,=3)Fig.5 Recovery of displacements on elements (m=2,=3)

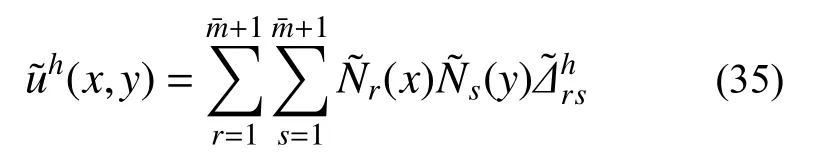
求解：

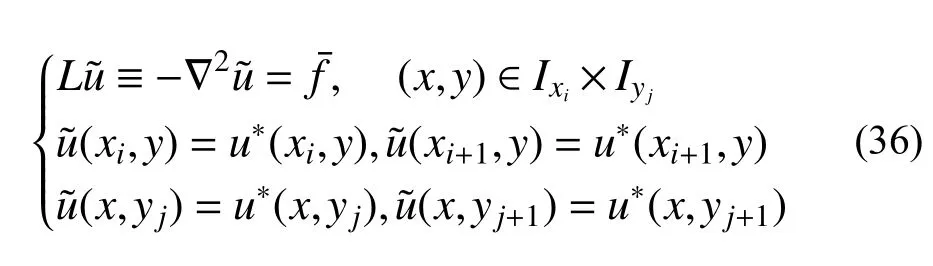
由于边界自由度均被固定，故此步只需求解单元内部自由度。逐单元进行上述求解，即可得全域超收敛解：

由二维有限元解答的收敛性估计[1]知：

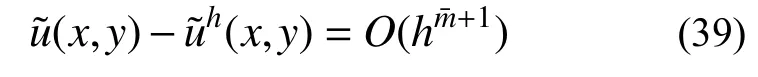
结合式(38)、式(39)可知超收敛解误差为：

数值结果表明，u*(x,y)的导数∂u*(x,y)/∂x、∂u*(x,y)/∂y亦具有如下的超收敛性：

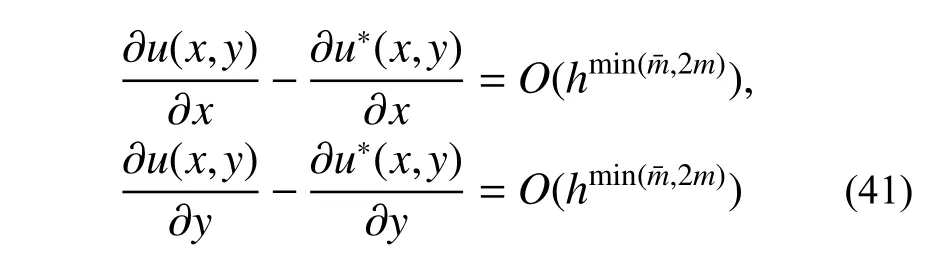
上述精度修复策略亦可推广至任意四边形网格。具体实施时亦是先修复单元边界，再修复单元内部。修复单元边界时，同一单元的相对边同时进行修复，为使相邻单元在公共边上的修复解相同，有公共边的单元同时参与修复计算，所有参与对边修复计算的单元构成一子网格，在该子网格上用m×次单元求解原控制方程，对对边解答进行修复(对边方向取为次，剩余对边方向保留m次)，并将单元剩余对边的解取为原有限元解，子网格在域边界上的边界条件取为与原问题一致，如图6 所示。单元内部解答修复过程与矩形网格相同。

图6 非规则网格四边形单元边位移恢复(m=2,=3)Fig.6 Recovery of displacements on edges of quadrilateral elements on irregular mesh(m=2,=3)

对于任意四边形网格，由于受单元畸变[20]的影响，网格结点的位移精度有所下降，不一定具有h2m阶的超收敛性，但相对于单元内部位移，网格结点位移仍具有更高的精度。应用本文方法，仍可有效提高解答的精度和质量，使位移尤其是应力的精度得到显著提升。

3 数值算例

本文算法已编成Fortran 程序。本节给出三个数值算例以展示其在不同求解区域、不同网格划分条件下对有限元解答质量和精度的恢复效果。对全域或子域误差均以最大模度量：

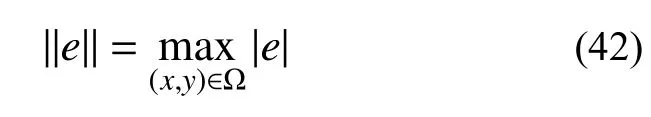
记超收敛解的误差为：

其x向、y向导数误差分别为：

定义超收敛导数误差为：

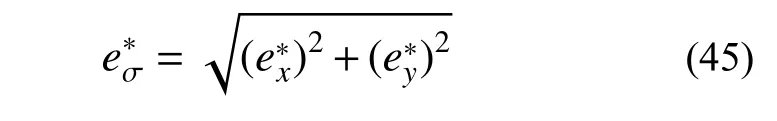
限于篇幅，例1、例2 导数收敛阶统计中只给出了x向导数的结果，y向导数具有与x向导数同样的收敛规律。

例1.矩形域规则划分问题

本例探讨矩形域规则划分解泊松方程问题。如图7所示，其控制微分方程及边界条件为：

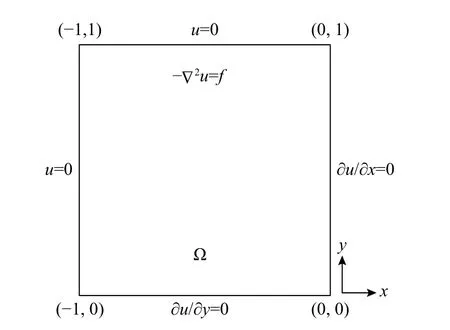
图7 例1 问题模型Fig.7 Problem model in Example 1

该问题的精确解为：

图8 例1 在(4×4)网格下 eh 与 e*分布的比较(m=1,=2)Fig.8 Comparison of ehand e*distribution on(4×4)mesh in Example 1(m=1,=2)

图9 例1 在(4×4)网格下分布的比较(m=1,=2)Fig.9 Comparison of and distribution on(4×4)mesh in Example 1(m=1,=2)

将求解域均匀剖分为(2×2)初始网格，并进行均匀二分加密，考察并统计(m=3,=4)、(m=3,=5)、(m=3,=6)、(m=3,=7)情形下本算法位移及导数的收敛阶规律，结果如表1 和图10 所示。经超收敛计算后，位移解和导数解的精度均得到显著提高，解答收敛阶随超收敛次数的提高而提高，但都不超过网格结点位移解的收敛阶h2m。收敛阶规律与式(40)、式(41)中的估计吻合。表2 列出了(m=3,=4)情形下有限元求解及超收敛计算的时间对比，可见随有限元求解规模的增大，超收敛计算的耗时占比快速下降，充分体现了本文算法的修复过程计算量小、效率高。

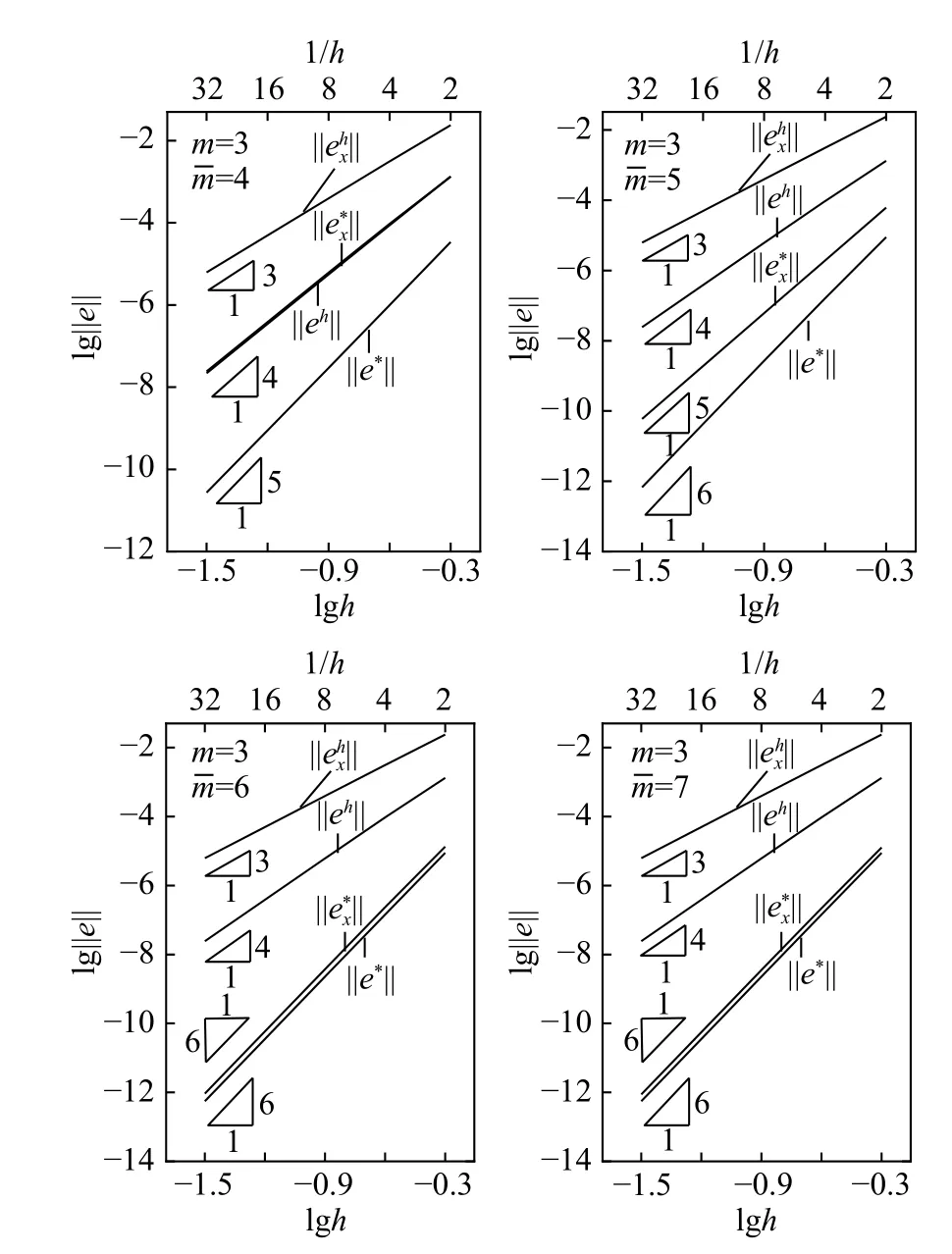
图10 例1 有限元与超收敛解收敛阶Fig.10 Convergence order of FE solution and recovered solution in Example 1

表1 例1 有限元与超收敛解的误差和收敛阶Table 1 Error and convergence order of FE solution and recovered solution in Example 1

表2 例1 有限元与超收敛过程计算时间(m=3,=4)Table 2 Computation time of FE solution and recovered solution in Example 1(m=3,=4)

表2 例1 有限元与超收敛过程计算时间(m=3,=4)Table 2 Computation time of FE solution and recovered solution in Example 1(m=3,=4)

例2.非规则四边形域规则划分问题

本例探讨非规则四边形域规则划分解泊松方程问题。其求解域 Ω如图11 所示，其控制微分方程及边界条件为：

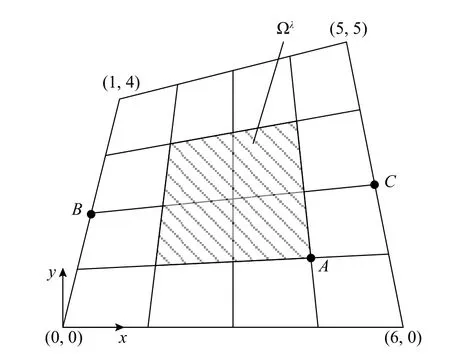
图11 例2 模型的求解域及网格划分Fig.11 Domain and mesh of Example 2

由于在一般边界条件下，边界层网格结点位移解的天然超收敛性相对较差[22]，这会导致该区域修复解的精度相对差些。为检视本文方法对域内解答的修复效果，本文取一典型内子域 Ωλ(由均匀4×4 网格划分中内部4 个单元构成的子域)考察解答误差的变化情况，如图11 所示。为探讨四边形域规则网格下有限元网格结点位移解的收敛阶，采用双二次元(m=2)、双三次元(m=3)、双四次元(m=4)进行有限元计算，提取(4×4)网格结点A(4.375,1.1875)位移误差值边界层(始终靠近边界的一层单元)网格结点最大位移误差值，统计其收敛阶具体见表3。图12 展示了在(64×64)规则网格下(m=3)情形下BC 网格线上有限元结点位移误差的分布情况。可见，域内部网格结点位移收敛阶可达最佳收敛阶次h2m；而受非规则区域边界的影响，靠近边界的一层单元角结点位移收敛阶仅为hmin(2m,m+2)。

表3 例2 有限元网格结点位移误差和收敛阶Table 3 Error and convergence order of mesh node displacement of FE solution in Example 2

图12 例2BC网格线上有限元结点位移误差(Fig.12 ErrorofFEnoded√isplacements on BC mesh line inExample

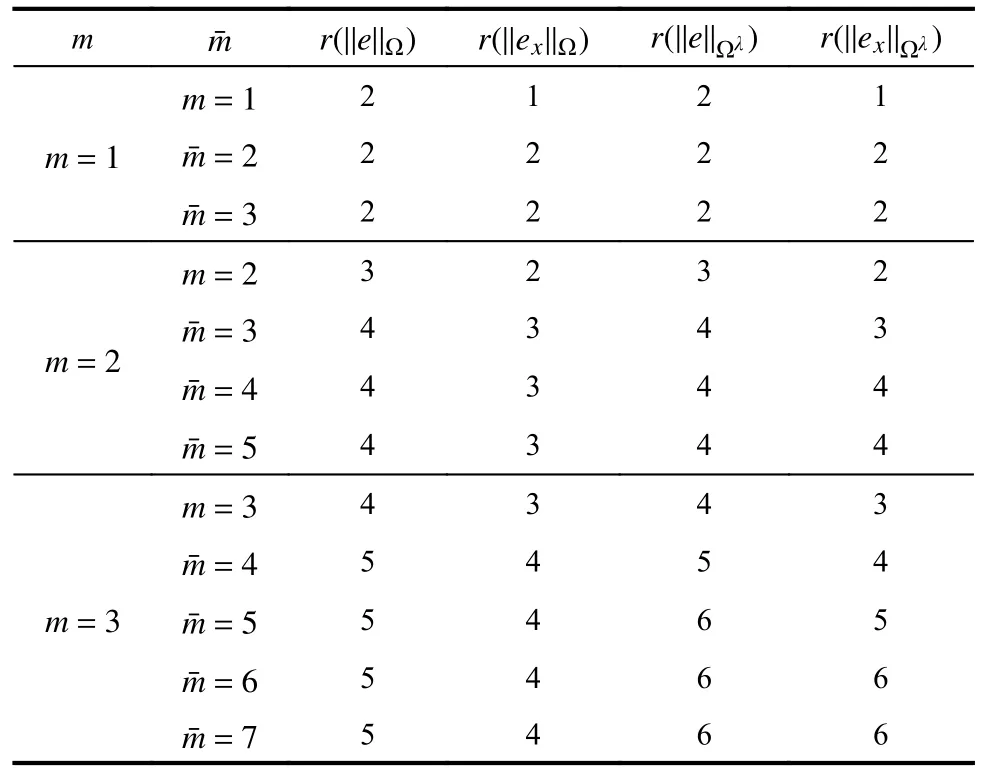
表4 例2 有限元和超收敛解收敛阶Table 4 Convergence order of FE solution and recovered solution in Example 2

图13 例2 有限元与超收敛解收敛阶Fig.13 Convergence order of FE solution and recovered solution in Example 2

图14 例2 在(32×32)网格下分布(m=2,=4)Fig.14 Distribution of on(32×32) mesh in Example 2(m=2,=4)

例3.矩形域非规则划分问题

本例探讨矩形域非规则四边形网格划分解泊松方程问题。采用HyperMesh 软件[24]作网格划分，得图15 所示网格，记该网格划分为J 剖分，对该网格进行均匀二分加密得到的网格划分记为K 剖分。本例控制微分方程及边界条件为：

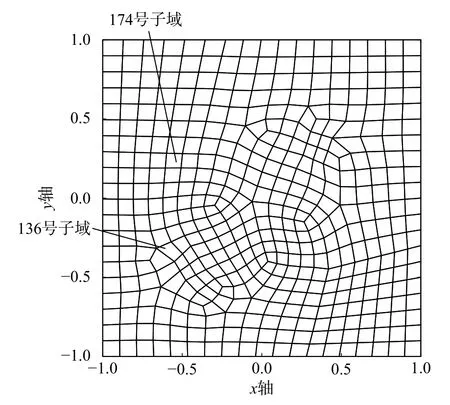
图15 例3 模型的求解域及网格划分Fig.15 Domain and mesh of Example 3

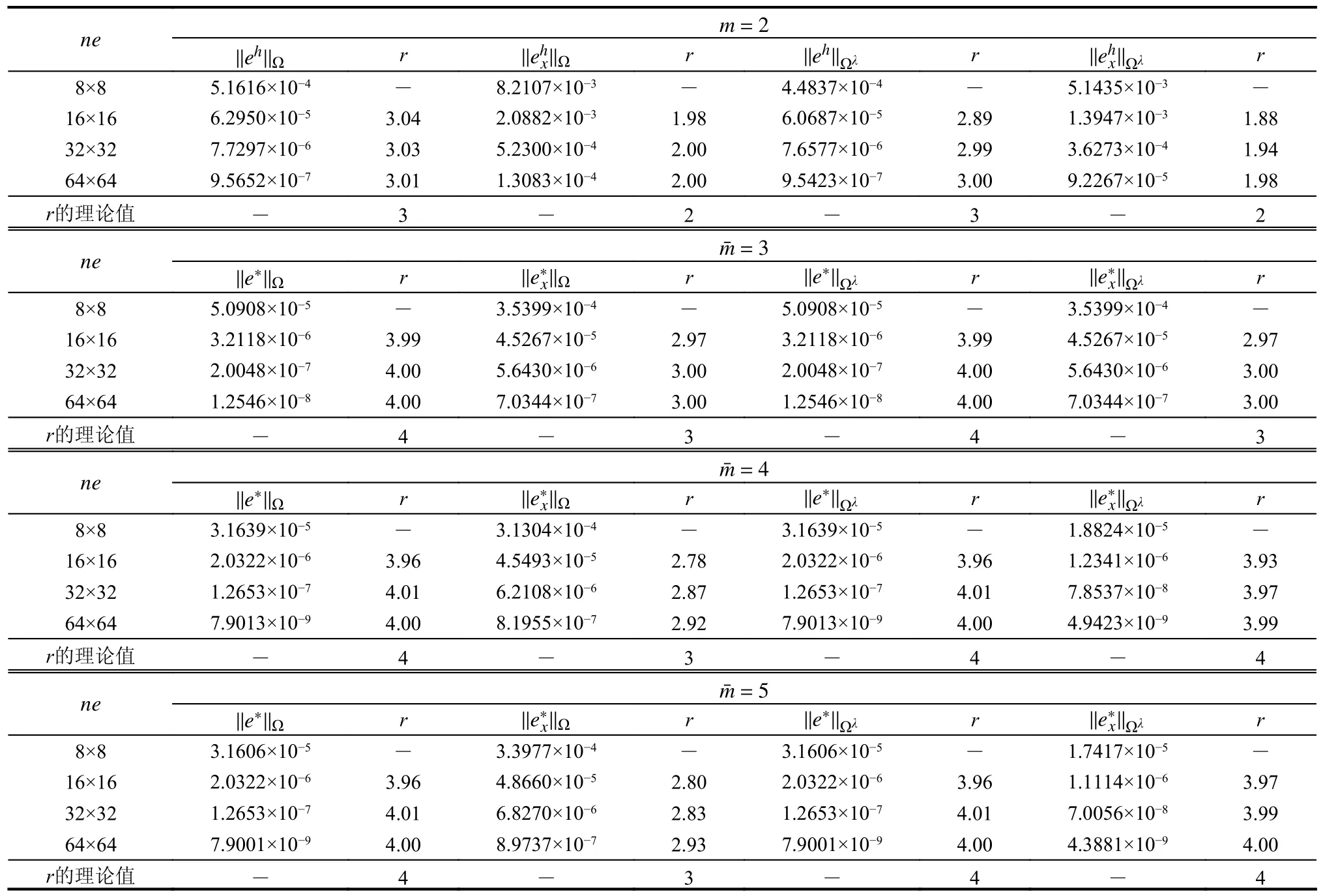
表5 例2 有限元与超收敛解的误差和收敛阶(m=2)Table 5 Error and convergence order of FE solution and recovered solution in Example 2(m=2)

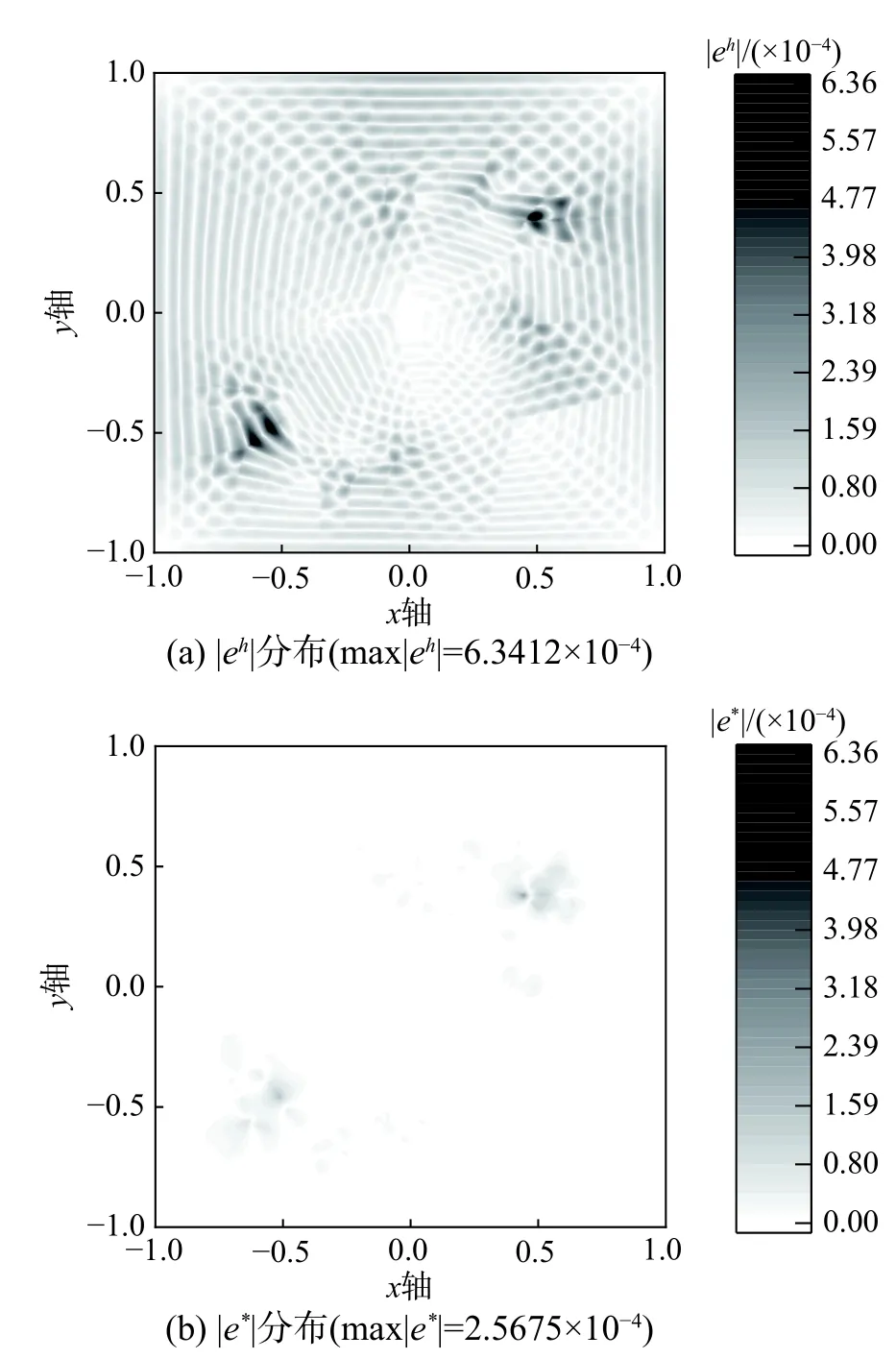
图16 例3 在J 剖分下 |eh| 与 |e*|分 布的比较(m=2,=3)Fig.16 Comparison of |eh| a nd |e*| distribution on J mesh in Example 3(m=2,=3)

在最大模度量下，可见对上述问题，均可将全域位移(包括非规则区域)误差恢复至网格结点水平。对于(m=2,=3)情况J 剖分下规则区域位移误差比为3.00%，K 剖分下该误差比进一步降低至1.74%。可见随网格加密，规则区域修复的位移呈加速收敛之势，即经超收敛恢复后，规则域位移收敛阶可得到提高。因非规则划分不满足变换的强正规条件，故非规则区域网格结点位移往往不具有超收敛性质[18]。但该区域网格结点位移精度仍优于单元内部，本文方法可将单元域内位移恢复至网格结点水平，故非规则域位移误差仍有显著下降，全域位移误差比(由非规则域控制)为40%左右，部分非规则区域位移误差比为20%左右。

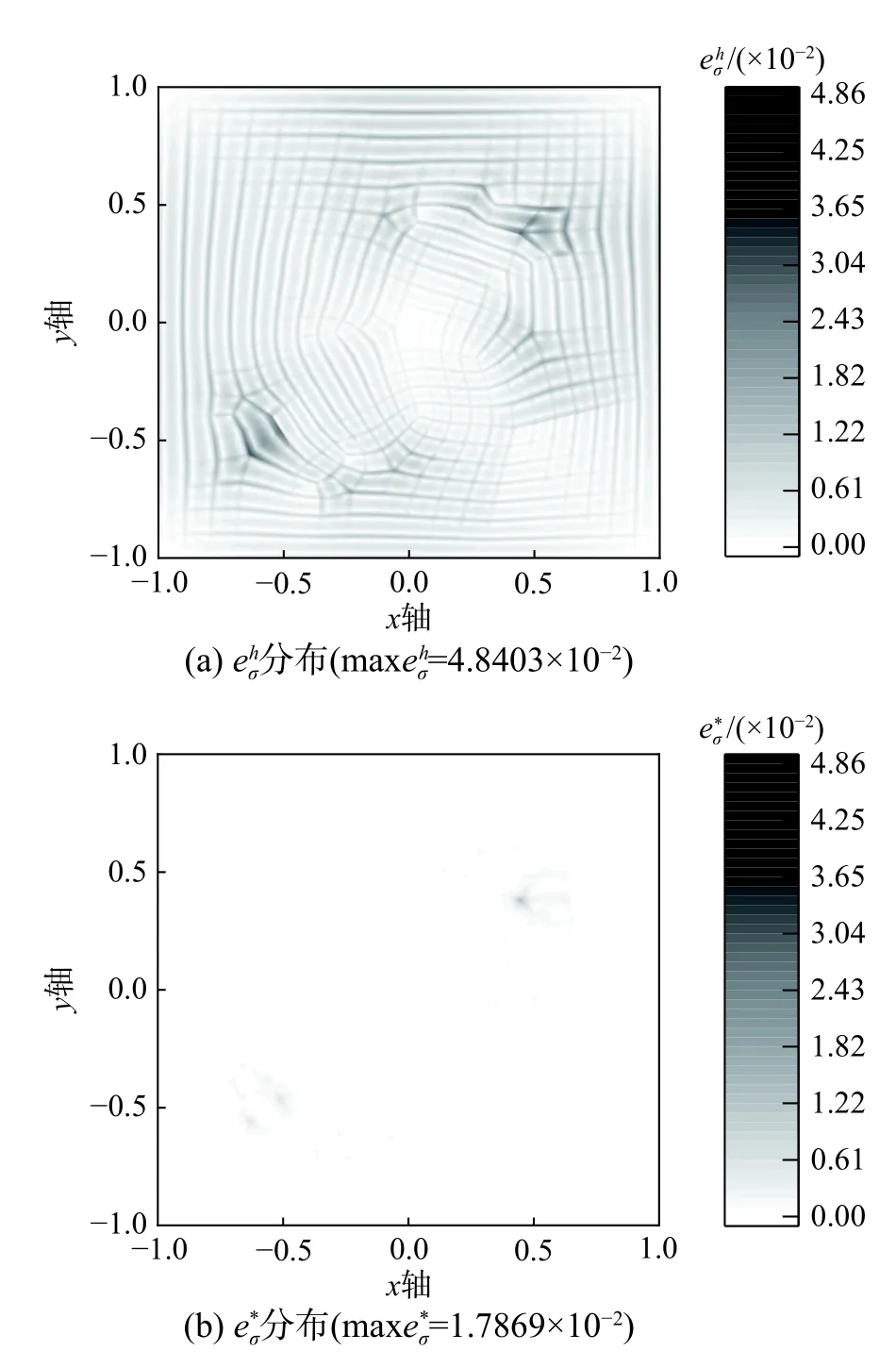
图17 例3 在J 剖分下分布的比较(m=2,=3)Fig.17 Comparison of distribution on J mesh in Example 3(m=2,=3)

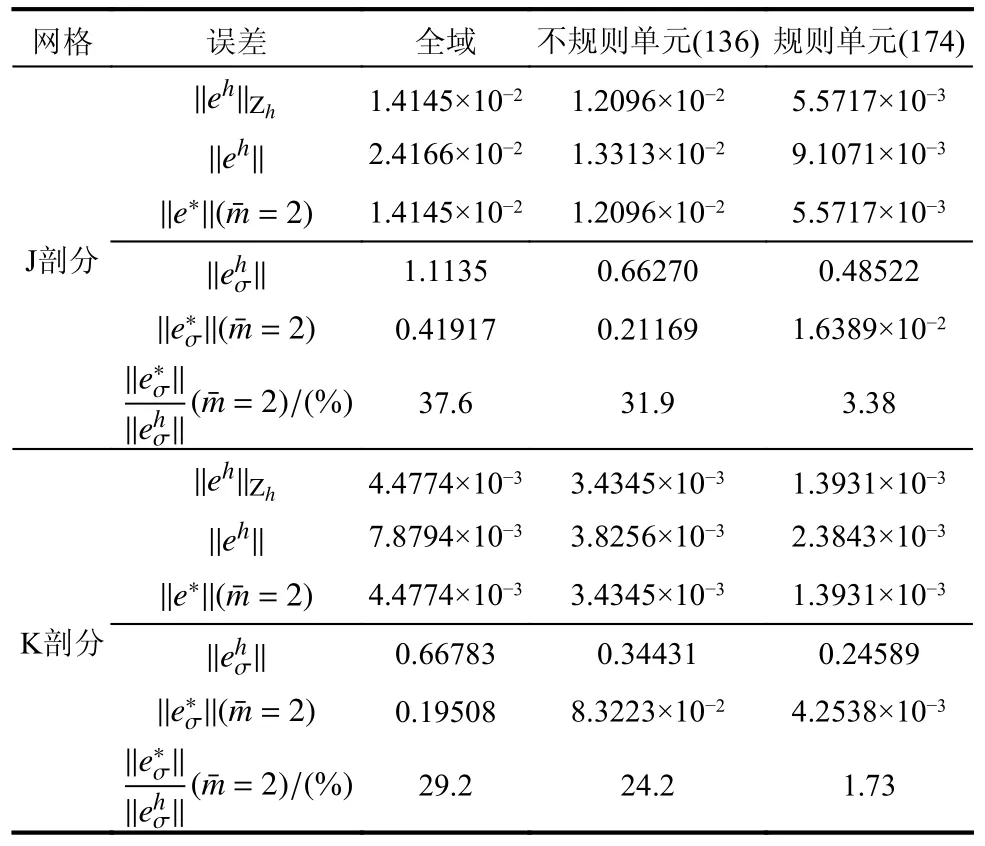
表6 例3 有限元和超收敛误差(m=1)Table 6 Error of FE solution and recovered solution in Example 3(m=1)

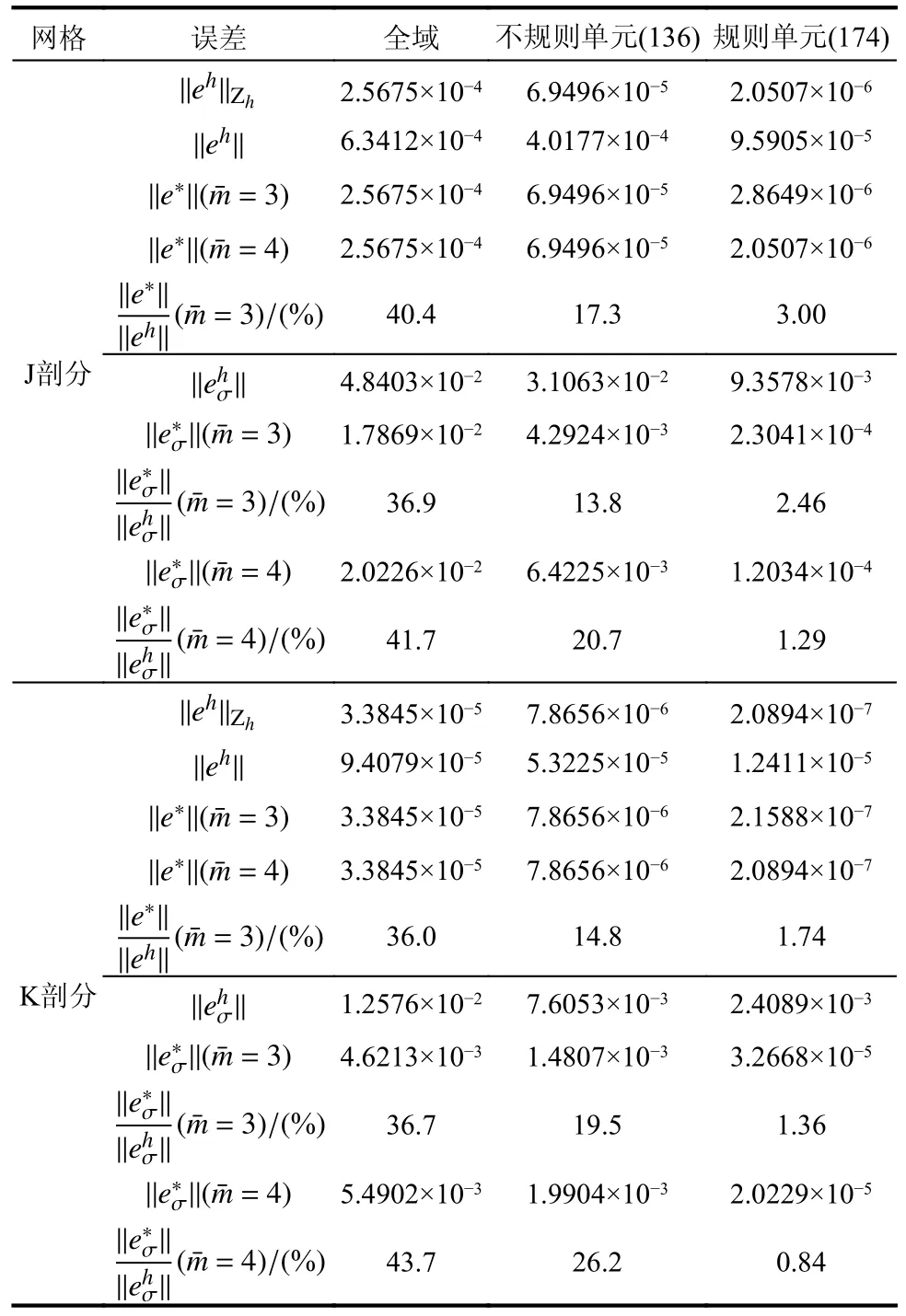
表7 例3 有限元和超收敛误差(m=2)Table 7 Error of FE solution and recovered solution in Example 3(m=2)

综上，对于非规则网格问题，虽然有限元的求解精度较差，本文算法对解答精度仍有明显的提升效果。

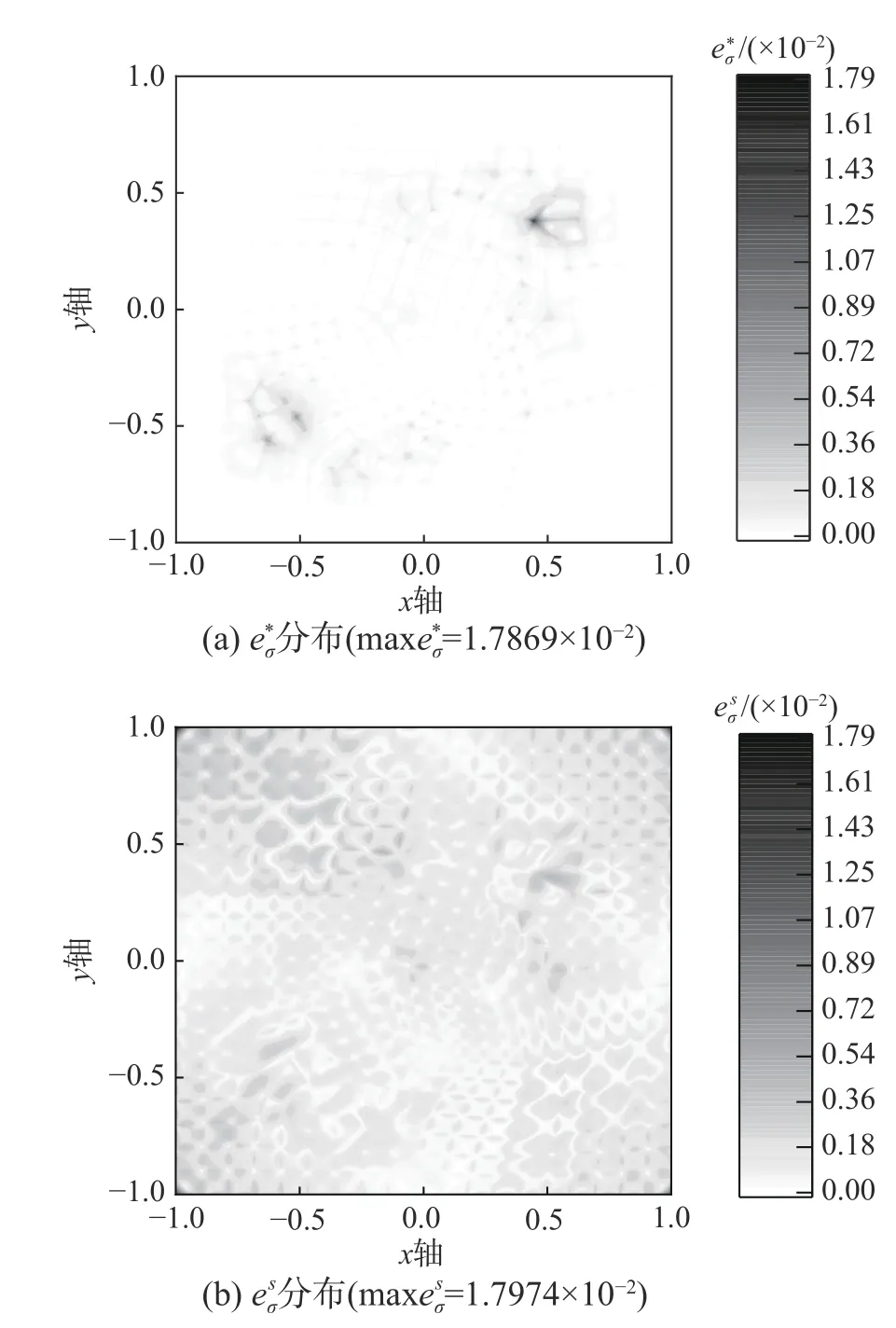
图18 例3在J 剖分下(m=2,=3) 与分布的比较Fig.18 Comparison of(m=2,=3)anddistribution on J mesh in Example 3

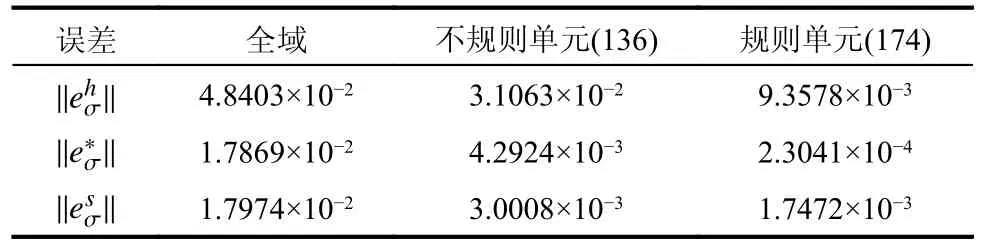
表8 例3 本文算法与SPR 法的误差对比Table 8 Error comparison of this method and SPR in Example 3

4 结论

在非规则域规则网格划分下，求解域的内部子域仍具有上述的超收敛效果。但在边界层附近，导数精度仅能提高一阶。

对非规则网格划分，规则域的有限元解答精度明显优于非规则域。本文方法对规则域和非规则域的精度均有明显提升效果，规则域的精度提升明显优于非规则域。

本文方法通过在一系列子网格上作有限元求解获取超收敛解，计算量小，而解答的精度和质量均有显著提高，且方法易于推广。故本文算法具有进一步研究的价值。