横向地震作用下震致钢轨几何不平顺研究

蒋丽忠，余 建，周旺保，冯玉林，彭 康，左永健

(1.中南大学土木工程学院，长沙 410075；2.中南大学高速铁路建造技术国家工程实验室，长沙 410075；3.华东交通大学土木建筑学院，南昌 330013)

钢轨不平顺是指钢轨的几何形状、尺寸和空间位置发生相对于正常情况的偏差。受到施工误差、构件变形以及自然环境作用等多方面因素影响，钢轨不平顺是普遍存在的。钢轨不平顺是引起高速列车振动的主要激扰源之一[1-3]，为了保证列车运行的安全性和舒适性，有必要对钢轨不平顺的特征、分布规律及影响展开研究。

近年来，学者们针对温度变化[4-6]、基础不均匀沉降[7-10]、混凝土徐变[11-14]、钢轨焊缝[15-19]、构件刚度退化[20-23]等多种因素引起的钢轨不平顺均展开了研究。但目前关于研究地震导致的钢轨不平顺的文献仍很少。中国的高速铁路建设逐渐向山区地震断裂带和沿海地震高烈度区延伸[24-28]，高速铁路桥梁遭遇地震的几率大大提升。铁路运输作为抗震救灾的重要生命线，在抗震救灾期和灾后重建期承担了极其重要的运输任务，研究震致钢轨不平顺是保证震后行车安全的基础。

因此，本文建立了带CRTS Ⅱ型轨道系统的高速铁路简支梁有限元模型并进行了试验验证，研究了横向地震作用后钢轨残余不平顺的分布规律，对震后钢轨残余不平顺的平稳性进行了验证，基于随机振动理论和假设检验原理分别提出了平稳震致钢轨几何不平顺功率谱密度曲线、非平稳震致钢轨几何不平顺功率谱密度曲面的确定方法，构造了震致钢轨几何不平顺样本，为震后行车速度阈值的确定提供不平顺输入。

1 高速铁路系统有限元模型及其验证

1.1 高速铁路系统有限元模型

以8 度地震区内一座采用CRTS Ⅱ型板式无砟轨道的多跨简支梁作为研究对象(图1)。主梁采用长度32.5 m 的标准预应力混凝土箱梁，桥墩采用圆端形实体墩，支座采用竖向承载力为5000 kN的盆式橡胶支座，防落梁装置间隙设为20 cm。底座板为宽2.55 m、高0.19 m 纵向通长结构，底座板与主梁之间铺设6 mm 厚的滑动层。轨道板结构是用张拉锁件连接相邻底座板上的纵向钢筋形成的纵向连续结构，截面尺寸为2.55 m × 0.2 m，轨道板与底座板之间填充厚度3 cm 的CA 砂浆层。钢轨采用CHN60 型轨，扣件类型为WJ-8C 型。剪力齿槽设置在固定支座上方的梁体表面。剪切钢筋设置在梁缝两侧的轨道板和底座板之间。侧向挡块设置在桥面上，相邻挡块纵向相距6.5 m。采用ANSYS 建立有限元模型，箱梁、底座板、轨道板、钢轨模拟为弹性梁单元，单元长度设置为0.65 m。桥墩模拟为考虑弯矩-曲率曲线的广义梁单元。连接构件采用非线性弹簧进行模拟，本构关系如表1 和图2 所示[24-26]。

图1 高速铁路轨道-桥梁系统示意图Fig.1 Structural diagram of high-speed railway track-bridge system

表1 非线性弹簧单元的本构曲线Table 1 The force-displacement curves of the spring elements

图2 非线性弹簧单元的本构曲线Fig.2 The force-displacement curves of the spring elements

1.2 模型验证

为了验证有限元模型的正确性，对一座11 跨高速铁路简支梁桥缩尺模型开展了振动台试验[24,26](图3)，试验的相似系数见表2。振动台试验系统由4 个边长为4 m 的6 自由度振动台组成，试验区域的最大长度为55 m，适用于大跨度桥梁结构的抗震试验。缩尺模型的试件制作遵循以下原则：1)为了便于制作和安装，试件整体采用钢材进行加工制作；2)主梁、桥墩、底座板、轨道板和钢轨在地震中一般不发生明显损伤，因此，在试件的设计中不考虑它们的非线性，根据等效刚度原理，试件的弯曲刚度设计为原型刚度与刚度相似系数SS的乘积；3)滑动层、砂浆层和扣件在结构内力的传递中发挥着重要作用，因此，根据等效力和等效位移原理对试件进行设计，对不同尺寸的试件进行屈服力和屈服位移测试，选择屈服力和屈服位移与原型相似程度最高(SF和SL)的尺寸作为试件尺寸；4)剪力齿槽、剪切钢筋和侧向挡块在地震中通常没有明显变形，因此，它们的试件设计得足够坚固。通过振动台对模型施加地震激励，记录下结构响应并与有限元模型进行比较。通过振动台对模型施加地震激励，记录下结构响应并与有限元模型进行比较(图4)。可以看到，有限元模型地震响应的形状和幅值与实测数据基本一致，表明有限元模型能够比较准确地模拟结构的振动。

表2 振动台试验相似系数Table 2 similarity coefficient of shaking table test

图3 振动台试验Fig.3 The shaking table test

图4 结构横向地震响应Fig.4 Lateral response of structure under the action of earthquakes

2 横向地震作用后钢轨残余不平顺的分布规律

桥址位于8 度区，对应的设计地震峰值加速度为0.2g，场地的特征周期分区为一区，场地类别为Ⅰ类，场地的反应谱特征周期为0.25 s。结合上述信息生成场地的设计反应谱，导入PEER 强震数据库并从中筛选出40 条和设计反应谱匹配程度最高的地震动作为有限元模型的横向地震输入。

将有限元模型的简支梁跨数取为30，墩高取为14 m。为了模拟路基段对桥梁结构的约束效应，分别对第1 跨简支梁固定端和第30 跨简支梁滑动端的底座板、轨道板、钢轨施加固定约束。将40 条加速度输入的峰值分别调整为0.2g和0.38g(8 度区设计和罕遇地震峰值加速度)，在每一条地震输入的尾端增加一段10 s 的零值段以模拟地震停止后结构的自由振动(图5)，对有限元模型开展非线性时程分析。从有限元模型中提取震后钢轨残余位移，将左右钢轨的横向、竖向位移分别记为yl、yr、zl、zr；将钢轨的轨距、高低、轨向、水平不平顺分别记为Ig、Iv、Ia、Ic。它们满足下列关系：

图5 地震动输入(1971，San Fernando 地震，地震台：Pacoima Dam)Fig.5 Ground motion input (1971,Earthquake:San Fernando,Seismic Station:Pacoima dam)

结合式(1)～式(4)生成震后钢轨残余不平顺(图6)。可以看到，钢轨的轨距、高低和水平不平顺的幅值较小，轨向不平顺的幅值较大，这是由于桥墩的横向屈服力大于支座，在横向地震作用后桥墩整体保持弹性状态，而支座的横向残余变形较大。轨向不平顺的幅值随PGA 的提高大幅增长，表明支座的损伤和残余位移随着地震强度的提升显著增加。因此，震后钢轨残余轨向不平顺有可能成为列车震后行车速度的主要控制因素，本文将以其作为主要的研究对象。

图6 40 组震后钢轨残余不平顺Fig.6 Residual rail irregularity after 40 earthquakes

残余轨向不平顺主要集中在0 m～200 m 和800 m～1000 m 范围内，在200 m～800 m 范围内钢轨相较于初始位置发生了整体偏移，这是由于桥梁两端的钢轨将受到路基段约束效应的影响，而约束效应的影响范围大约在200 m。这个结论表明对于采用CRTS Ⅱ型板式无砟轨道的高速铁路多跨简支梁，靠近路基约200 m 范围内的震后钢轨残余轨向不平顺需要特殊考虑；其余空间范围内的不平顺特征相对稳定，其不平顺特征可以通过一个较小的空间样本展开预测。高速铁路简支梁桥的跨数往往可以达到几十甚至上百，过多的简支梁数量将引起有限元分析工作量的显著增加，这个结论对于有限元模型的简化具有重要意义。

3 震后钢轨残余不平顺的平稳性验证

3.1 平稳性验证方法

若将震后钢轨残余不平顺视为一组空间序列，那么其平稳性是指该序列在任意空间范围内的统计特性(均值、方差、协方差等)保持不变。对震后钢轨残余不平顺平稳性的检验具有重要意义，主要体现在：1)若震后钢轨残余不平顺在空间上具有平稳性，那么就可以通过截取一个较小的空间样本来对任意空间范围内的钢轨不平顺特征展开计算；2)残余不平顺是否具有平稳性对于其分析方法具有决定性影响，平稳随机信号适合采用傅里叶变换进行分析，而非平稳随机信号的分析则应该基于短时傅里叶变换、小波分析等时频分析方法。因此，本节将结合随机振动理论和假设检验原理，对震后钢轨残余不平顺的平稳性展开检验。首先，将不平顺样本(y1,y2,···,yN)记为YN，构造集合A(y1,y2,···,yN-1)和集合B(y2,提出零假设H0：YN是非平稳随机过程；对应的备择假设H1为：YN是平稳随机过程。构造统计量t：

lAA、lAB、sn可分别表示为：

式中：t为分布临界值；α为显著水平(α=0.05)。当不平顺样本的h2=0 时，则应考虑该不平顺样本为非平稳序列；当不平顺样本的h2=1 时，可认为该不平顺样本是平稳序列。

3.2 实例分析

将图6 中的轨向不平顺分别划分为0 m～200 m的L1段，200 m～800 m 的L2段，以及800 m～1000 m的L3段。对40 组钢轨残余轨向不平顺的平稳性进行检验，如图7 所示。可以看到，对于所有地震动，L1段和L3段的h2均等于0，表明L1段和L3段不平顺为非平稳序列；对于绝大部分地震动，L2段的h2均等于1，表明L2段不平顺可近似按照平稳序列进行处理。

图7 震后钢轨残余轨向不平顺的平稳性检验结果Fig.7 Smoothness test results of rail residual track irregularity after earthquakes

4 平稳震致钢轨几何不平顺的构造

4.1 构造方法

信号同时具备时间特征和频率特征。对于平稳随机信号，信号特征往往体现在频谱特性上，而傅里叶变换是分析信号频谱特性的常用工具。因此，本节将结合傅里叶变换和假设检验原理，构造一种具有保证率的平稳震致钢轨几何不平顺。将震后钢轨残余不平顺的样本及其离散傅里叶变换记为η(n)和F(f)，它们满足：

式中，n、N、f分别为不平顺数据点的序号、总量以及频率点。不平顺样本的功率谱密度曲线记为G(f)，存在：

将i条地震波(i=1,2,···,I)对应的G(f)曲线记为Gi(f)，将各个频率上对应的i个数据点记为gi，gi的常用对数集合记为Xi。采用假设检验原理中的k-s法来检验Xi的正态性，定义函数F(k)：

记Φ、μ、σ为标准正态分布、样本Xk的均值和方差，定义函数F0(k)：

式中，zα为标准正态分布上的分位点。连接各个频率的上界Xu，得到震后钢轨残余不平顺功率谱密度上界曲线Xr(f)。在随机地震作用下Xi是不确定的，但由Xi的特征参数生成的Xu是唯一的，因此Xr(f)可以用于预测震致钢轨几何不平顺。采用多项式S(f)对Xr(f)进行拟合，震致钢轨几何不平顺的时域样本 ηT可以表示为：

式中：m、M为频率点的编号和总量；φ(m)为(0,2π)上均匀分布的独立随机变量；Δf为频率点间隔。将采样速度记为V，震致钢轨几何不平顺的空间样本 ηS可以表示为：

4.2 实例分析

基于第3 节和第4 节的结论，选取L2不平顺段开展平稳震致钢轨几何不平顺的构造，步骤如下所示：

1)根据式(9)～式(10)，生成40 条震后钢轨残余轨向不平顺的功率谱密度曲线G(f)(图8)。

图8 功率谱密度曲线G(f)Fig.8 Power spectral density curve G(f)

2)根据式(11)～式(15)，将每一频率上40 个功率谱密度曲线点集合记为g40，g40的常用对数集合记为X40，对X40的正态性进行验证(图9)。不同频率上X40的J2计算值均为0，表明X40内的数据点满足正态分布。

图9 系数J2Fig.9 Coefficient J2

3)根据式(16)～式(17)，计算并连接各个频率的上界Xu得到震后钢轨残余轨向不平顺的功率谱密度上界曲线Xr(f)(图10)。

图10 功率谱密度上界曲线Xr(f)Fig.10 Upper bound curve of power spectral density Xr(f)

4)根据Xr(f)的形状特征，以lg(f)=-0.7为界限，左侧和右侧分别采用三次多项式和线性方程进行拟合，得到表达式S(f)(图11)。

图11 功率谱密度上界曲线表达式S(f)Fig.11 Expression of upper bound curve of power spectral density S(f)

5)根据式(18)～式(19)，计算震致钢轨几何不平顺样本 ηS(图12)。

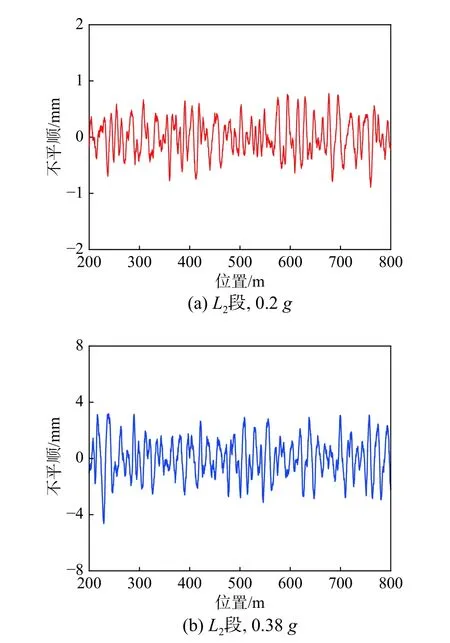
图12 震致钢轨几何不平顺Fig.12 Rail geometric irregularity caused by earthquakes

6)根据式(10)计算 ηS的功率谱密度曲线并与S(f)比较(图13)，可以看到两者的位置基本贴合，表明生成平顺样本 ηS的正确性。

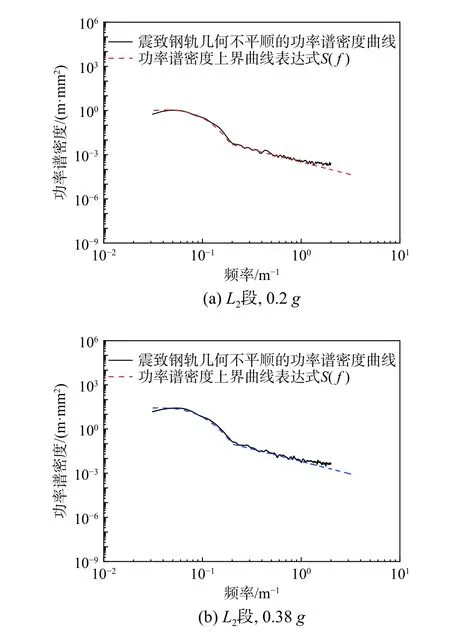
图13 震致钢轨几何不平顺的功率谱密度曲线Fig.13 Power spectral density curve of rail geometric irregularity caused by earthquakes

5 非平稳震致钢轨几何不平顺的构造

5.1 构造方法

对于非平稳信号，信号往往需要从频率特征和时间特征两方面展开分析，但傅里叶变换不具备分析信号时间特征的能力。因此，本文引入短时傅里叶变换对非平稳信号的时频特性展开研究，并结合假设检验原理，构造一种非平稳震致钢轨几何不平顺。

短时傅里叶变换的原理是将信号分帧加窗，对每个窗口内的信号开展傅里叶变换，计算并拼接不同时间窗口上的频率特征从而得到整个信号的时频信息。对于震后钢轨残余不平顺的样本η(n)，其离散短时傅里叶变换为：

式中：DTFT为离散时间傅里叶变换；w为窗函数；t为窗函数的偏移时间；f为频率。窗函数的种类较多，本文采用hamming 窗，即：

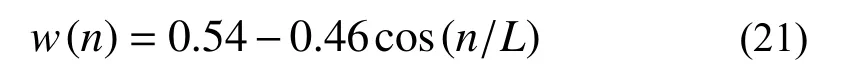
式中，L为hamming 窗的长度。样本的功率谱密度曲面为：

式中，Fs为采样频率。将i条地震波对应的功率谱密度曲面Gη(t,f)记为Gi(t,f)，将坐标(t,f)上对应的i个曲面点记为gi(t,f)，gi的常用对数集合记为Xi(t,f)。

采用式(11)～式(15)检验Xi的正态性。若对于所有(t,f)，Xi均能满足正态性检验，则采用式(16)～式(17)计算所有(t,f)上的上界Xu。连接各Xu得到样本的功率谱密度曲面上界Xu(t,f)。此时，对于任意一条地震波的功率谱密度曲面Gi(t,f)，存在：

因此，非平稳震致钢轨几何不平顺η(n)可以表示为：

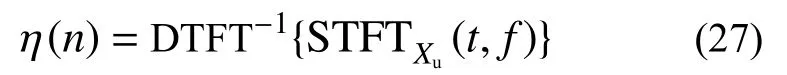
式中，DTFT-1为离散时间傅里叶逆变换。

5.2 实例分析

选取L1段开展非平稳震致钢轨几何不平顺的构造，步骤如下所示：

1)以0.1 m 为空间间隔对L1段不平顺插值取点，时间采样频率设为1024，根据式(20)～式(23)，生成包含40 个震后钢轨残余轨向不平顺功率谱密度曲面的集合G(图14 展示了San Fernando 地震作用后的钢轨残余轨向不平顺功率谱密度曲面)。

图14 震后钢轨残余轨向不平顺的功率谱密度曲面(San Fernando 地震)Fig.14 Power spectral density surface of rail residual track irregularity after earthquake (Earthquake:San Fernando)

2)根据式(11)～式(15)，将各个(t,f)上的40 个功率谱密度曲面点集合记为g40，g40的常用对数集合记为X40，对X40的正态性进行验证(图15)。可以看到，所有(t,f)上的J2都等于0，表明各个(t,f)上的功率谱密度曲面点满足正态分布。

图15 系数J2Fig.15 Coefficient J2

3)根据式(16)～式(17)计算所有(t,f)上的上界Xu。连接各Xu得到样本的功率谱密度曲面上界Xr(t,f)(图16)。

图16 功率谱密度曲面上界曲面Fig.16 Upper bound of power spectral density surface

4)根据式(23)～式(27)，计算非平稳震致钢轨几何不平顺η(n)(图17)。

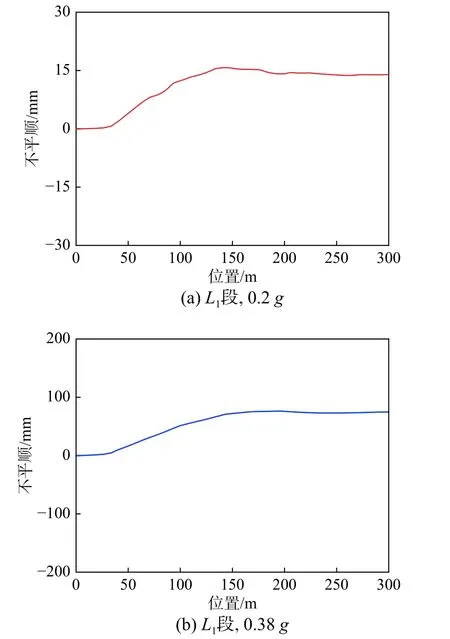
图17 非平稳震致钢轨几何不平顺Fig.17 Nonstationary rail geometric irregularity caused by earthquakes

5)根据式(22)，生成非平稳震致钢轨几何不平顺的功率谱密度(图18)。可以看到，其自然对数的曲面形状与Xr(t,f)(图16)基本一致，证明了上述方法的正确性。

图18 非平稳震致钢轨几何不平顺的功率谱密度曲面Fig.18 Power spectral density surface of nonstationary rail geometric irregularity caused by earthquakes

6 结论

本文研究了横向地震作用后钢轨残余不平顺的分布规律，对震后钢轨残余不平顺的平稳性进行了验证，基于随机振动理论和假设检验原理分别提出了平稳震致钢轨几何不平顺功率谱密度曲线、非平稳震致钢轨几何不平顺功率谱密度曲面的确定方法，构造了震致钢轨几何不平顺样本，获得如下主要结论：

(1)震后钢轨残余轨距、高低和水平不平顺的幅值较小，轨向不平顺的幅值较大，这是由于桥墩的横向屈服力大于支座，在横向地震作用后桥墩整体保持弹性状态，而支座的横向残余变形较大。

(2)对于采用CRTS Ⅱ型板式无砟轨道的高速铁路多跨简支梁，震后钢轨残余轨向变形主要集中在靠近路基约200 m 的范围内；其余空间范围内的轨向不平顺特征相对稳定，其不平顺特征可以通过一个较小的空间样本进行预测。

(3)靠近路基约200 m 的范围内的震后钢轨残余不平顺应按照非平稳信号进行处理，其余空间范围内的轨向不平顺可近似按照平稳信号进行处理。

(4)在随机地震作用下，平稳钢轨残余不平顺在各个频率的功率谱密度服从对数正态分布，非平稳段不平顺在各个时间-频率节点上的功率谱密度服从对数正态分布。震后钢轨残余不平顺震致钢轨几何不平顺可通过震后钢轨残余不平顺谱集合的均值和方差简单表示。

(5)平稳震致钢轨几何不平顺的功率谱密度可采用多段多项式函数拟合，计算形式简单，便于手算，为基于行车安全性能的高速铁路桥梁抗震设计方法提供了重要的理论基础。