非对称独塔混合梁斜拉桥的异形索塔不同状态力学性能分析

阳佳丁，李济川，梅继洲，周 锐，朱德权

（1、广东佛盈汇建工程管理有限公司 广东佛山 528000；2、中交第二公路勘察设计研究院 武汉 430050；3、深圳大学土木与交通工程学院 深圳 518000）

0 引言

近年来，随着桥梁技术的快速发展，独塔混合梁体系斜拉桥因其兼具混凝土梁和钢梁的优点和良好的力学性能，在桥梁工程建设中得到广泛应用［1］，例如1972 年建成的世界上首座独塔双跨混合梁斜拉桥德国ku-sehumaeher 桥以及2017 年我国建成的最大主跨跨度为338 m的广州东沙特大桥。由于索塔结构是独塔混合梁斜拉桥的灵魂构建，为了使桥梁造型与现代化城市建设相呼应，城市景观桥梁索塔开始向异形化发展，目前主要有曲线形索塔、折线形索塔、钻石形索塔和花瓶形索塔等［2］。索塔锚固结构是斜拉桥重要传力构件之一，然而异形索塔的构造复杂，局部区域的应力集中问题明显，是斜拉桥设计、施工的重要关注对象。

已有一些学者针对异形索塔斜拉桥的受力特征进行了研究，曾明根等人［3］采用空间有限元模型详细模拟索塔中各部分构件，计算索塔中钢锚箱板件的应力和混凝土的应力，分析斜拉索索力在索塔锚固区的传递分配关系；吴万忠等人［4］针对异形索塔斜拉桥关键节点建立板壳模型，并进行空间应力分析；杨斐等人［5］对介绍了混凝土索塔钢锚箱的设计特点并进行了受力分析；孙鹏［6］对非对称独塔单索面预应力混凝土斜拉桥静载试验；张亮亮等人［7］建立了斜拉桥索塔锚固区的实体有限元模型，对比分析了3 种不同工况下锚固区的受力特点及应力分布规律；李艳凤等人［8］分析了折线形索塔的力学特性，并重点研究了索塔折角处的受力；段政等人［9］对钢锚箱各构件和钢箱梁腹板单元进行局部细化，对纵向弧形独塔的索塔钢锚箱结构的应力状态和应力分布规律进行仿真分析；叶建龙等人［10］采用ANSYS 软件建立钢锚箱及其对应的主梁边箱节段锚固区的三维实体有限元模型，分析锚固区的受力特性，并分析锚固区关键板件厚度及斜拉索索面倾角调整的2 步优化方法；刘新华等人［11］选取塔顶5 对斜拉索的锚固区段为对象，设计制作1∶4 的缩尺模型进行静载试验，并采用MIDAS FEA 软件建立索塔锚固区有限元模型，分析锚固区塔壁和锚块的应力分布。异形索塔结构不能采用传统的平面杆系模型进行分析，必须通过实体模型分析其三维应力状态；且由于不同施工状态下索塔锚固区所受到的荷载不同，导致其局部应力状态会有很大程度的差异。因此有必要对各施工状态下斜拉桥及其索塔锚固区的应力进行详细分析。

本文以一座独塔混合梁斜拉桥为工程背景，其索塔线型采用佛手型的异形结构，分别建立全桥的梁单元有限元模型和异形索塔结构的实体有限元模型，分析不同施工阶段全桥及索塔锚固区结构的空间受力和变形分布，研究结果为异形索塔斜拉桥的设计和施工提供重要的参考价值。

1 非对称独塔混合梁斜拉桥

以一座跨径为200+114=314 m 的非对称单塔空间双索面混合梁斜拉桥为工程背景。该桥采用塔墩梁固结体系，主跨采用“PK”断面钢箱梁（梁高为3.5 m，宽为38.6 m），边跨采用“PK”断面的混凝土双边箱梁（梁高为3.14 m，宽为38.6 m），主桥总体布置如图1 所示。主塔采用“佛手”造型的变截面混凝土塔，塔高125 m，横梁以上塔柱高102 m，材料为C50 混凝土，内部拉索锚固区为钢锚梁结构，共15 套钢锚梁30 对斜拉索，拉索采用1 860 MPa 钢绞线。钢锚梁由钢板组合而成，其支撑结构为钢牛腿，由上承板、托架板、塔壁预埋钢板、剪力钉和与劲性骨架相连的连接钢板组成，钢板材料为Q345qC。

2 不同施工阶段下桥塔受力特征

2.1 桥塔自立状态

对于桥塔自立状态，混凝土塔柱采用爬模施工，边跨混凝土主梁采用支架现浇施工，主跨钢箱梁采用桥面起重机吊装施工。此时桥塔最大位移出现在塔顶，为6.05 mm，最大压应力出现在横梁中点，为1.82 MPa，如图2所示；桥塔最大横桥向压应力出现在横梁与塔的交点处，为2.95 MPa，由横梁自重引起，故桥塔自立状态下的主塔应力、应变最大值都满足设计安全要求。

图2 桥塔自立状态应力Fig.2 Stress of a Bridge Tower in a Self-supporting State

2.2 混凝土跨满堂支架状态

对于混凝土跨满堂支架状态，桥塔最大位移出现在塔顶，为6.023 mm，最大压应力出现在横梁中点，为1.41 MPa，如图3所示；桥塔最大横桥向压应力也在横梁与塔的交点处，为2.72 MPa，故混凝土跨满堂支架状态下的主塔应力、应变最大值都满足设计安全要求。

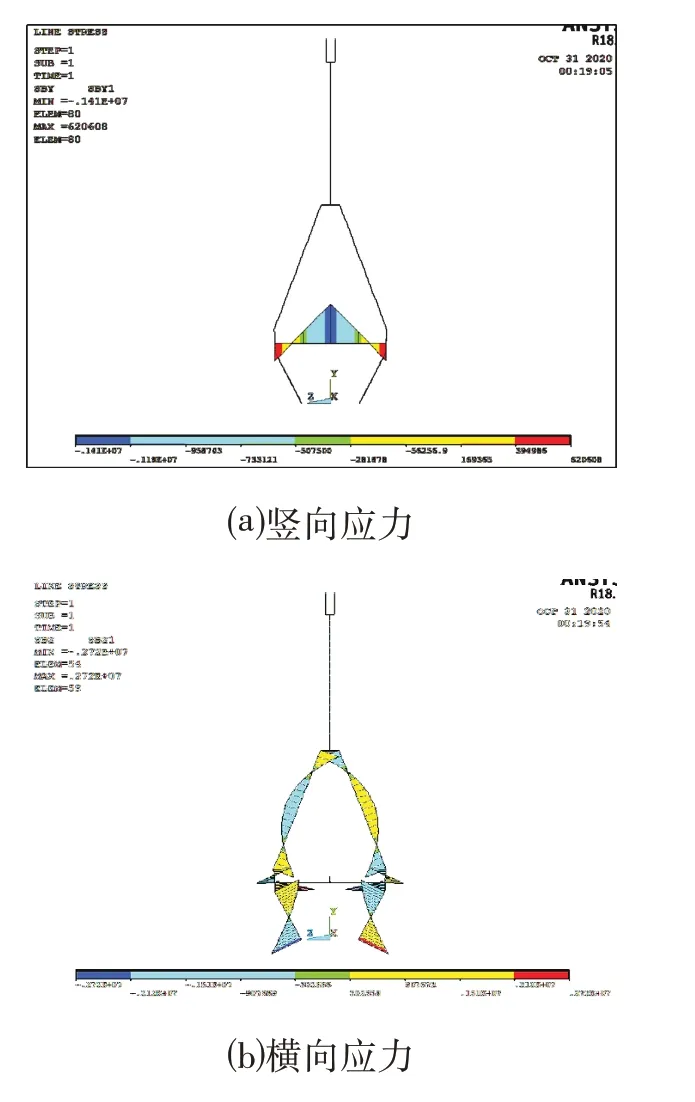
图3 桥塔满堂支架状态应力Fig.3 Stress of Bridge Tower in Full Hall Bracket State

2.3 最大悬臂状态

桥塔最大悬臂状态下，桥梁最大位移出现在主跨的跨中处，为6.223 mm，最大压应力出现在主梁主跨左梁端，约为33.1 MPa，如图4 所示；桥塔最大横桥向压应力出现在横梁与塔的交点处，为3.98 MPa。桥塔最大悬臂状态下主塔的最大应力以及拉索的最大应力和成桥阶段应力分布相似，但应力大小值小于成桥状态下的应力，故最大悬臂状态下其他的位移和应力均满足设计要求，整体桥梁受力较为安全。

图4 桥塔最大悬臂状态应力Fig.4 Stress of the Maximum Cantilever State of the Pylon

3 索塔锚固区局部应力分析

3.1 桥塔实体有限元模型

对异型桥塔采用实体建模，对索锚固区混凝土变截面塔进行多段划分来模拟曲线，主塔实体模型选用SOLID95 单元，混凝土塔和钢锚梁之间用Conta174 和Targe170连接单元模拟刚接，主塔边界条件为主塔根部底面固接的形式来模拟，塔身锚固区节段顶部设为自由端，将选取节段承受的荷载施加到结构上，比如结构自重，节段以上塔身重量和拉索索力值，节段底部采用固结方式模拟，具体的实体有限元模型和桥塔的变形如图5所示，在最大悬臂施工阶段和成桥阶段，主塔的最大变形均出现在塔顶第一个锚固区，变形值为7.42 mm。

图5 索塔锚固区实体有限元模型Fig.5 Finite Element Model of Anchorage Zone of Pylon Tower

3.2 锚固区局部应力

在最大悬臂阶段工况下拉索拉力作用下，索塔锚固区混凝土塔应力分布规律为从上到下应力增大，如图6⒜所示，最大应力点出现在右下角的最后一个锚固区的中间位置，为70.1 MPa，建议加强这一区域的配筋。在成桥阶段在最大索拉力的作用下，锚固区桥塔应力分布规律也为从上到下应力增大，顺桥向从左到右应力增大，横桥向应力对称分布，最小应力点出现在左上角的第一个锚固区位置，最小应力为0.63 MPa，最大应力点出现在右下角的最后一个锚固区的中间位置，最大应力为25.3 MPa，如图6⒝所示。在成桥阶段最大索拉力的作用下，第一锚固区钢板的应力如图6⒞所示，最大应力出现在靠近牛腿区的下侧钢板侧，为76.2 MPa。

图6 不同状态的锚固区应力Fig.6 Stress of the Anchored Area in the Bridge State

4 结论

本文主要针一座非对称独塔混合梁斜拉桥，分别进行了不同施工阶段的整体结构受力分析和索塔锚固区的受力分析，具体结论如下：

⑴最大悬臂状态的桥塔最大位移和应力要明显大于桥塔自立状态和满堂支架状态，受力最危险的区域在于钢混结合锚固区以及钢梁左端端部区域，但不同施工阶段的变形与受力仍满足设计要求。

⑵对于索塔锚固区，施工阶段最大应力点出现在右下角的最后一个锚固区的中间位置，应力分布规律为从上到下应力增大，最大应力为70.1 MPa；成桥阶段工况钢梁主要的大应力出现在靠近牛腿区的下侧钢板侧，应力值从两侧到中间呈减小趋势，最大应力为76.2 MPa。