软土深基坑桩撑支护选型分析及数值模拟研究

刘 芳，罗 武，赵永志，朱汉新，杨 烁

（珠海市建筑设计院 广东珠海 519000）

0 引言

随着我国城市化和地下空间利用的发展，基坑工程近年来有了快速的发展［1］。考虑到深基坑工程越来越多，复杂的周边环境及周边管线对现代工程基坑变形及稳定性要求越来越高［2-3］。基坑开挖过程中，土体的变形与土体的性质和土体的固结渗流等因素密切相关［4］，珠海地区软土区域分布广泛，属于滨海沉积软土，具有低强度、高压缩性、触变性及低透水性等工程性质，作为建筑物地基极易发生不均匀沉降，而对于复杂环境下的深基坑支护工程，变形量的控制成为基坑工程成败的关键，同时考虑到软土工程性质和深基坑边界条件的复杂性，岩土工程理论发展的滞后性，使理论计算分析和预测值和实际监测值存在较大的差距，至今仍存在很多的问题。因此，软土地区基坑开挖的理论模型和支护结构的工作机理、承载特性研究内容尚需完善。

本文以珠海软土地区某深基坑为例，首先进行支护型式选型分析，然后分别采用理正深基坑软件和MIDAS/GTS 有限元软件对基坑开挖过程进行有限元模拟分析。经过验证对比分析，数值分析能很好地反映基坑开挖过程中土体的性状，使得分析的结果能更好地反映土体的真实变形特性，为软土地区深基坑工程实践提供一定的理论依据，为后续类似工程积累设计和施工经验。

1 基坑支护选型和设计

1.1 基坑支护选型

拟建工程为一栋48层超高层办公楼，地下室2层，深基坑工程开挖深度为9.5 m，基坑周长约449 m，基坑总面积约14 130 m2，基坑呈方形。根据场地周边管线资料，场地南侧、西侧及北侧均有10 kV 供电线、电信线、污水管、路灯、雨水管，市政管线分布复杂。根据现场钻探揭露及室内土工试验结果，场地内分布的地层为人工填土层（Qml）、第四系海相沉积层（Qmc）、残积层（Qel）及燕山期侵入岩（γ52（3）），各土层物理力学参数如表1所示。场地地下水主要赋存在素填土及基岩风化带风化裂隙中，砂质粘性土含水层之上有填土层覆盖，与地表水水力联系较弱，与下部基岩强风化带的裂隙水有微透水，测得稳定水位埋深0.40～2.30 m。

表1 各土层物理力学参数Tab.1 Physical and Mechanical Properties of Soil Layers

本工程开挖深度较深，且地质条件差，存在松散填土，淤泥广泛发育且埋深较厚，邻近基坑周边有市政道路，路面下埋设有较多市政管线。若基坑支护及止水措施不当，开挖将产生大变形，对市政道路及管线的稳定带来不利影响，因此，本工程支护设计选型的关键在于严格控制位移及做好止水帷幕，使周边既有建筑和市政管线的位移和沉降满足基坑支护设计相关规范要求，减少对周边环境的影响。

鉴于基坑开挖深度较深，周边环境要求较严格，土钉墙或是复合土钉墙支护难以满足变形的要求，不适宜位移要求较严的深大复杂的基坑；桩-锚支护可确保基坑壁土体变形可控，但限于基坑周边建筑和管线要求，不宜采用预应力锚杆支护结构［5-6］。考虑到基坑施工时对变形控制等必要条件，目前超大深基坑支护常采用工艺相对成熟的的内支撑加排桩的组合，将坑内外不平衡的水土压力施加于排桩上从而保持受力平衡，最后传到稳定的结构体系上，且不受地层条件控制［5-7］，因此本工程支护结构采用钻孔灌注桩加混凝土内支撑型式。

1.2 基坑支护设计

经各种支护型式对比，拟采用放坡加桩撑支护，放坡高度为2.5 m，坡率为1∶1。支护桩为直径1 200 mm，间距1 400 mm 混凝土灌注桩；设置一道混凝土内支撑，均为角撑间距为8～9 m，未设置腰梁，内支撑标高同冠梁层标高；使用直径为600 mm 的高压旋喷桩作为灌注桩桩间土加固及止水作用，坑内软弱土体加固采用直径为800 mm搅拌桩格栅布置。

采用理正深基坑计算软件建立三维整体模型（见图1），四边地面超载均按照均布荷载20 kPa 考虑，所有土层均设置为水土合算，设置3 个阶段施工工况：①开挖至3.5 m；②开挖至坑底；③拆除支撑。计算所得的水平变形曲线、支撑轴力、支护桩内力分别如图1、图2所示。

图1 三维整体模型及水平变形曲线Fig.1 Three-dimensional Whole Model and Horizontal Deformation Curve

图2 支护桩弯矩及支撑轴力Fig.2 Bending Moment and Axial Force of Supporting Pile

根据理正三维计算结果，基坑开挖至坑底时，基坑支护桩桩身变形最大值为40.42 mm，位置位于阳角边长最长区域，支护桩弯矩最大值为2 629 kN·m，支撑轴力最大值为8 482 kN。软件计算结果满足基坑支护设计相关规范要求，说明支护型式选取的合理性和可靠性。

2 MIDAS/GTS软件施工过程数值模拟

MIDAS/GTS 是一款应用于岩土与隧道分析的有限元软件，已经广泛应用于实际岩土工程的设计和施工［8］。本文将采用MIDAS/GTS 有限元软件对深基坑支护工程进行实体建模，基于连续介质力学有限元方法，模拟施工过程中各开挖工况，分析各种工况下周边土体的沉降、支护的内力及水平变形、支撑轴力及坑底隆起值，进一步说明数值模拟研究深大基坑的可行性。

2.1 模拟分析参数取值

2.1.1 三维模型的建立

基坑长123 m，宽122 m，深9.5 m，根据基坑开挖深度的影响区域及土层分布特点取基坑X方向计算长度为296 m，Y方向计算长度为220 m，Z方向深度取31 m，整体三维区域为296 m×220 m×31 m。数值模型包括土体、围护结构、水平支撑体系等，整体模型网格划分如图3 所示，共有1 321 572 个节点，212 501 个单元。计算区域的四面及底面施加位移约束，地表为自由边界，Z轴负向施加重力加速度，坡顶四边3～9 m 区域施加20 kPa施工荷载。

图3 模型网格划分示意图Fig.3 Sketch Map of Model Grid Division

本文使用如下3 个计算假定：①使用总应力法分析计算结果，计算过程中可暂不考虑固结和地下水渗流对工程的影响；②施工过程中不考虑时间效应，仅考虑基坑设置的时空效应；③土体与基坑围护结构使用节点位移耦合，忽略土体与基坑围护结构之间的相对位移，未设置围护结构与土体之间的界面单元［5，7，9］。

2.1.2 单元设置

模型网格划分中，土体本构模型选用修正摩尔-库伦本构模型。土体单元设置为各向同性三维实体单位。结构体应用线弹性模型，其中混凝土支撑、立柱及冠梁使用梁单元模拟；MIDAS GTS 板单元可考虑平面受拉、受压、平面受剪、平面外受弯、厚度方向剪切，基于厚板理论开发的，同样适用于薄板，本工程放坡喷射混凝土面层及支护桩采用板单元模拟，其材料参数如表2所示。排桩按照抗弯刚度等效方法转化为桩墙［1］，折算后的地下连续墙厚度h为：

表2 支护体系材料参数Tab.2 Material Properties of Retailing Structures

其中：D为钻孔桩桩径，D=1.2 m；t为桩净距，t=0.2 m；支护桩采用一字相切排列，等价后的地下连续墙厚度h=0.955 m。

2.2 模拟结果分析

2.2.1 基坑开挖过程中位移的变化

基坑开挖至坑底时，桩身水平位移如图4所示，基坑开挖过程中，不同阶段桩身水平位移随深度的变化过程如图5所示。

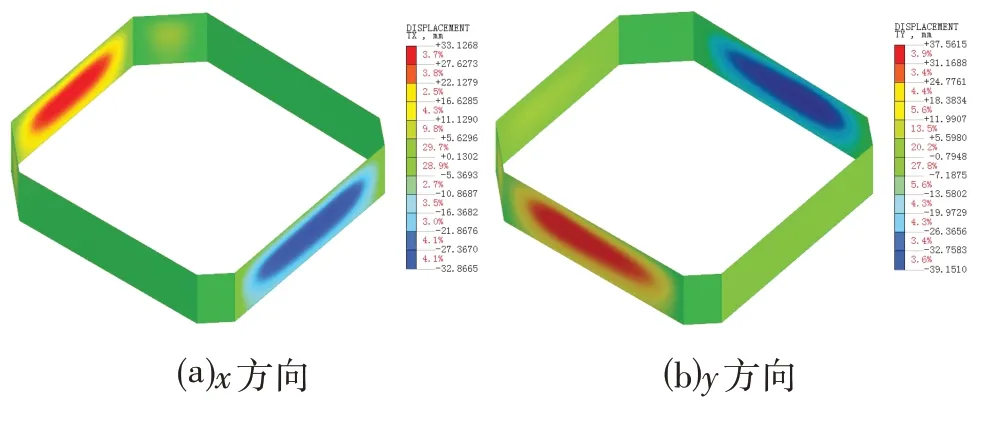
图4 排桩位移云图Fig.4 Displacement of Nephogram for Row Piles

图5 排桩水平位移曲线Fig.5 Deformation Curve of Row Piles

通过对2 种工况下支护桩水平位移曲线进行分析，可知2 种工况下桩侧变形基本保持一致。随着开挖深度的不断加深，最大位移点不断下移，基坑水平位移不断增加，因支护桩两端承受支撑轴力和被动土压力约束，两端位移受到限制，支护桩呈现明显的中间大、两端小“鼓肚状”特点。开挖至第一层土，即内支撑标高下移0.5 m 处，桩顶及桩端的水平位移分别为1.5 mm 和4.5 mm；开挖至坑底时，桩顶、坑底及桩端水平位移分别为16 mm、38 mm、16 mm；桩侧水平位移最大值为39 mm，与基坑深度比值约为0.41%，位置为距离坑底以下1.6 m，约为基坑深度的1/5。

出现这种现象的原因分析：当因开挖深度较浅，且设置刚度较大的混凝土内支撑，而本基坑存在较厚软土层，60%的桩长处于淤泥中，桩端软弱土层的约束较弱，导致工况1 情况下桩端水平位移相对较大。当开挖至坑底时，桩侧水平位移总体的变化趋势保持一致，但因软弱土层的黏聚力和内摩擦角值相对较小，导致桩侧变形较大，桩端的水平位移也相对较大，被动区土自身变形也较大，对支护桩约束相对较弱。

开挖至坑底时，基坑周边不同位置处地表沉降量的变化值如图6所示。

图6 基坑周边地表沉降曲线Fig.6 Surface Settlement Curve Around Foundation Pit

根据MIDAS/GTS 不同工况下Z轴方向位移云图分析，可知随着基坑开挖的进行，地表不同位置处沉降逐渐增大。开挖至坑底时，由基坑周边地表沉降曲线变化趋势，距离坡顶0 m、9 m、80 m 的位置处，地表沉降量分别为2 mm、22 mm、0.2 mm；地表最大沉降量出现在离坡顶9～10 m 的区域，约为1 倍基坑深度；计算最大地表沉降量为22 mm，约为基坑开挖深度的0.23%；距离坑边1 倍坑深区域内，沉降量增加速率较大，距离坑边2～3 倍坑深区域内，沉降值迅速减少，距离坑边3 倍坑深的位置处，地表沉降量趋于稳定值。地表沉降主要由地表超载及地层中深厚软土引起的，地表沉降曲线呈现明显的“勺”型。

软基基坑开挖将引起墙厚相当范围内地表及地层沉降，这是基坑工程对环境的主要危害之一。地表沉降的大小与支护结构变形、坑底隆起及土体塑性流动的大小紧密相关，当开挖深度较大且土质软弱时，基坑周围土体塑性区范围相对较大，土体塑性流动也比较大，土体将会从支护结构外围向坑内和坑底流动，由此致使周边地表沉降量增加。同时根据地层补偿法原理，软弱土层存在塑性流动和塑性隆起的情况，本项目地表沉降由支护结构变形和坑底塑性隆起共同引起。

2 种开挖工况下，基坑底部不同位置处土体隆起量如图7 所示。由于侧向支护结构的限制，工况1 开挖至内支撑标高以下0.5 m 时，此时坑底土体为素填土，此阶段坑底隆起量呈现两端小中间大的变化规律，因基坑开挖面积较大，基坑长宽比接近1，靠近基底中心线的最大隆起量为29 mm，隆起量相对较大，但开挖深度不大，且坑底为素填土，坑底变形为弹性隆起，这种坑内回弹在开挖停止后很快停止，且基本不会引起基坑围护结构和坑外土体向内移动。

图7 基坑底部土体隆起量Fig.7 Surface Settlement Curve Around Foundation Pit

当基坑持续开挖后，内外高差不断增加，由于解除了土体的自重应力，坑底土体将产生回弹变形，同时开挖过程中围护结构及坑外土体在不平衡力的作用下向坑内移动，还将导致坑底土体产生负孔隙水压力，从而进一步导致坑底土体软化，吸水膨胀，使坑底进一步隆起。工况2开挖至坑底时，由于基坑较宽，开挖深度较大，基坑底部处于黏聚力和内摩擦角均较小的淤泥软弱土层中，从坑底土体隆起量变化曲线可知，底部出现塑性隆起，基坑两侧隆起量与中间区域隆起量相差较少，基坑底部整体隆起量达到110 mm，隆起变形量相对较大。

2种工况下坑底土体隆起曲线与实际开挖情况下土体隆起变形趋势较吻合，说明MIDAS/GTS软件计算的合理性，能较好地模拟基坑开挖过程中坑底土体的变形过程。

2.2.2 支撑轴力及支护桩弯矩的变化

支护桩折算为桩墙后的板弯矩云图及桩身的弯矩随深度变化曲线分别如图8、图9所示。

图8 开挖至坑底时支护桩弯矩云图Fig.8 Bending Moment Diagram of Retaining Piles during Excavation to Pit Bottom

图9 桩身弯矩随深度变化曲线Fig.9 Bending Moment Curve of Pile

通过分析可知，随着开挖深度的加大，同时冠梁位置处设置一道内支撑，桩身弯矩最大值的位置由桩顶向坑底桩身位置处移动，桩身弯矩最大值位于深度为9.5 m 处，软件计算弯矩值最大为1 944 kN·m/m；支护桩桩径为1.2 m，间距为0.2 m，软件计算值折算为支护桩的弯矩为2 721 kN·m，理正深基坑软件计算的桩身最大弯矩为2 629 kN·m，两者相差约3%。说明两者计算结果较相近，且与实际情况相符合。

基坑开挖至坑底时的内支撑轴力如图10 所示。本基坑设置放坡，仅布置一道内支撑，支撑的轴力随开挖深度的加深不断增加，开挖至坑底时，内支撑最大轴力稳定在7 117 kN，理正深基坑软件计算支撑轴力最大值为8 482 kN，两者相差1 365 kN。因基坑开挖面积较大，且长宽比接近1，基坑支护内支撑仅在四角区域设置角撑，其中夹角较大区域设置的支撑受力较为复杂，但整体上支撑的轴力均未超过材料抗力设计值，说明此工况下支撑处于安全状态。

图10 支撑轴力Fig.10 The Axial Force Curve of Struts

3 结语

本文结合有限元软件MIDAS/GTS，对某软土地区深基坑桩撑支护型式进行施工过程有限元模拟分析，并与理正计算结果进行对比，得到如下结论：

⑴基坑开挖初期至开挖到坑底，随着开挖深度加深，排桩水平位移最大值位置不断下移，水平位移曲线均呈现明显的“鼓肚状”型分布，中间大，两边小，最大值位于距离坑底约1/5的坑深处。

⑵基坑开挖过程中，周边地表沉降曲线呈现明显的“勺”型分布，模拟结果与实际情况相符合；基坑周边地表沉降最大值距离坑边约1 倍坑深，距离基坑越远，沉降影响越小，基坑对地表沉降影响范围约为1～3倍基坑深度。

⑶开挖中坑底为素填土时，坑底隆起量呈现中间大、两边小的规律；开挖至坑底时为淤泥软弱土层，基坑底部出现塑性隆起，基坑两侧隆起量与中间区域隆起量相差较少，基坑底部整体隆起量达到110 mm，隆起变形量相对较大。

⑷MIDAS/GTS 计算的支撑轴力及支护桩弯矩值与理正深基坑软件计算结果相近，说明分析结果的可靠性，与支护结构真实的受力及变形状况相符合，为软土地区上深基坑工程实践提供一定的理论依据，为深基坑设计与变形控制提供一定的理论指导。