城市软土复合地基施工钢波纹管拱涵的力学特性研究

杨雄峰，吴世栋，包小华，宋宇飞

（1、广东佛盈汇建工程管理有限公司 广东佛山 528000；2、深圳大学土木与交通工程学院 深圳 518000；3、中交第二公路勘察设计研究院有限公司 武汉 430000）

0 引言

钢波纹管属柔性管，结构简单、运输和施工方便，能较好地适应地基不均匀沉降。许多学者对钢波纹管涵洞（管涵、拱涵和管拱涵）进行了深入研究。YEAU 等人［1］和SEZEN 等人［2］对钢波纹管涵洞进行了现场静态和动态荷载试验，分析荷载类型、管涵几何形状、回填高度和铺设年限等对结构的影响，重点监测并分析结构挠度变化。MAI等人［3］则通过现场试验侧重研究劣化对既有钢波纹管结构性能的影响。张红宇等人［4-5］通过现场试验，分析了圆形钢波纹管结构的受力变形规律。BEBEN［6］对跨度12.3 m 的土-钢桥性能进行了数值模拟，分析回填土过程对结构的影响，同时考虑了不同界面参数的影响；此外，还对跨度5 m 拱形钢波纹管性能进行了现场测试［7］。费东阳等人［8］采用数值分析研究了波形、壁厚、填土方式和管顶覆土深度等不同因素对圆形钢波纹管力学特性的影响。冯忠居等人［9］通过室内模型试验，分析了圆形钢波纹管涵洞中间断面的力学特性、管周土压力及涵管变形规律。杨晓华等人［10］采用离心模型试验的方法，研究了不同路堤填筑高度、与路堤主线夹角及涵管直径对钢波纹管涵轴向、环向受力及变形特征的影响。地基加固效果同样会影响结构受力变形。陈甦等人［11］在考虑桩-土相互作用下的复合地基桩间土竖向变形模式下，推导了相关沉降理论公式。而数值分析中，难以充分考虑各种因素对符合地基的共同影响，最常见的方法就是视复合地基为均质体［12］。

综上所述，国内外学者研究的对象大部分是小～大直径的圆形钢波纹管或小跨度拱形钢波纹管，还未发现有与本文研究类似的在软土复合地基中施工多段（12 段）超大跨度（8 m、11 m）、高达7 m 的拱形钢波纹管的报道，因此，以广东省佛山市同济路西延线跨湖公路工程为依托，采用数值分析方法研究软土复合地基上施工超大跨度钢波纹管拱涵对结构受力变形的影响，以及拱涵桥自身的变形特征。

1 工程概况

1.1 桥涵和地层分布

如图1 所示，广东省佛山市同济路西延线是区域路网中一条由西向东延伸的集散公路，道路全长约1.54 km，途中k0+066.8～k0+300 跨越绿岛湖，与地铁四号线隧道共线，湖水常年深度约为1.09 m。如图2所示，跨湖段采用12 段钢波纹管连拱桥方案，桥长约140.8 m、宽约50 m，中部设置6段高跨7.77 m×11 m 的钢波纹管，两端分别设置3段高跨6.205 m×8.79 m的钢波纹管。管周回填轻填土，管顶平均覆土厚约2.7 m。隧道外直径为6.7 m，管片厚3.5 m，两隧道平均水平间距为6.3 m，由西至东隧道埋深逐渐增加，隧道拱顶与钢波纹管底部最小竖向间距为3.8 m。地层由上到下依次为：填土、淤泥质土、粉质黏土、中砂、强风化泥质砂岩、中风化泥质砂岩、中风化砂岩和中风化凝灰岩，湖底位于淤泥质土层上。

图1 跨湖段拱桥平面Fig.1 Plan of Arch Bridge Across the Lake

图2 地层分布及地铁工程加固处理范围剖面Fig.2 Strata Distribution and Section of Metro Engineering Reinforcement Treatment Range

1.2 拱涵基础与复合地基

软基处理断面设计如图3 所示，钢波纹管拱涵的基础由上到下为50 cm 砂砾垫层、150 cm 片石混凝土基础。基础下为φ850@600 mm 的三轴搅拌桩复合地基，地铁工程加固处理区域桩间距为1.5 m×2.4 m（即每排加固桩在水平面两个方向上的距离），处理深度为地铁底部设计高程；非区间隧道地基加固处理范围桩间距为2.05 m×2.9 m（同上），处理深度为10.0～31.5 m。

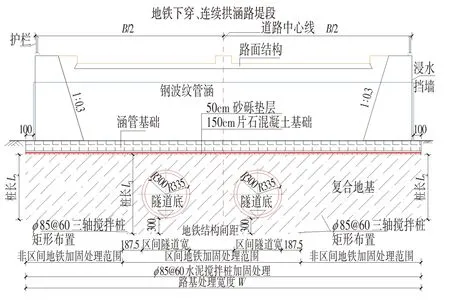
图3 软基处理断面设计Fig.3 Cross-section Design of Soft Foundation Treatment（cm）

2 室内试验和有限元模型

2.1 室内试验

为获取复合地基参数，对其钻心取样并测得抗压强度标准值，如表1 所示。根据前人研究可知，硬化土（HS）模型适用于软土和较硬土层，可以分析具有复杂应力路径的岩土工程问题［13-14］。因此，笔者进一步通过室内三轴试验获得基本参数，并通过式⑴拟合得到HS 参数［15］，黏土和中砂应力-应变曲线如图4所示，低围压和高围压分别表现出了应变软化、硬化的特性，验证了使用HS的合理性。

表1 取芯测试结果Tab.1 Coring Tests Results

图4 三轴试验应力-应变曲线Fig.4 Stress-strain Curves of Triaxial Tests

2.2 有限元模型

2.2.1 地层模型和本构模型

为尽量减小模型边界效应影响，根据经验，最终建立540 m×250 m×70 m（长×宽×高）模型，如图5 所示，采用混合网格形式划分，共计158 307 个网格节点、319 031个实体单元。结合上文，模拟中软土层、中砂层采用HS模型，岩石层采用摩尔库伦（MC）模型，片石混凝土基础、钢波纹管和隧道管片采用线弹性模型。

图5 计算三维模型Fig.5 3D Model of Calculation

2.2.2 地层计算参数

在模拟中，表1抗压强度无法直接使用，可根据文献［16-17］将抗压强度代表值换算为MC 模型参数。大部分参数通过详勘报告和三轴试验得到，对于一部分常见材料和没有条件通过试验获取的参数，参考类似工程或经验取值［15-20］，汇总后的地层参数如表2 所示。此外，计算中pref=100 kPa，νur=0.2，K0=1-sinφ′，Rf=0.9，ψ=φ′-30°（砂土），ψ=0（黏土），OCR=1.0=100 kPa。

表2 岩土层物理力学参数Tab.2 Physical and Mechanical Parameters of Rock and Soil Layers

2.2.3 钢波纹管模型及计算参数

钢波纹管材质为Q345钢材，波形为380mm×140 mm，壁厚分别为7.75 mm 和9.75 mm。由于数值分析中难以对钢波纹管的波纹进行三维建模，因此，根据王洋等人［21］提出的方法，按等效刚度法将钢波纹管等效为实心直管，等效结果如表3所示。

表3 支护结构计算参数Tab.3 Parameters of Supporting Structures for Calculation

2.2.4 施工过程模拟

实际的动态施工过程难以采用有限元精确分析，为尽量反映实际情况，需要在数值分析中做出一些合理假设：①复合地基视为均质体；②复合地基工程性质较好，不考虑地下水影响；③湖水压力等效为地层表面的法向压力；沥青混凝土路面自重等效为竖向荷载。模拟过程如下：①地应力平衡，位移清零；②移除钢波纹管基础位置的湖水压力，施工钢波纹管垫层，计算平衡；③一次性安装12 段钢波纹管，回填下轻填土，计算平衡（s2 阶段）；④回填上轻填土，计算平衡（s3阶段）；⑤一次性施工完成沥青混凝土路面拱桥路面，计算平衡（s4阶段）。

3 计算结果及分析

如图2所示，为了便于后续结果分析，将钢波纹管由左到右依次编号为1～12 号管，沿道路纵向取Ⅰ、Ⅱ和Ⅲ竖直剖面进行分析，其中Ⅰ、Ⅲ剖面分别距管口1 m，Ⅱ剖面位于中部。同时，将管截面测点位置按逆时针标记，如图6所示。

图6 钢波纹管截面测点标记Fig.6 Marking of the Measuring Point of the Cross Section of the Steel Corrugated Pipe

3.1 变形分析

3.1.1 地基基础变形

s2～s4 阶段3 个剖面的基础表面沉降曲线如图7所示，横坐标200～340 m 表示拱桥基础长度。在同一阶段3 个剖面的沉降基本一致，s2 阶段总体沉降较小，最大值（12 mm）位于6～7 号管处；s3 阶段沉降快速增加，相比前一施工阶段整体增加约13 mm，最大值（26 mm）出现在4～6 号管处，该位置下方的淤泥质土层厚较厚（见图2），由表1 可知，淤泥质土层处理后达不到设计标准，可能导致4～6 号管沉降比其他位置的管道大；s4 阶段沉降增量（3 mm）较小，说明铺设混凝土路面产生的自重荷载引起的基础沉降较小。

图7 基础表面沉降Fig.7 Settlement of Foundation Surface

图8为桥面3个剖面沉降曲线，横坐标190～350 m表示桥面长度，同一阶段3 个剖面沉降基本一致，s4阶段4～6 号管沉降增量（7 mm）最大，拱桥起止端沉降增量（3 mm）最小，符合上述基础沉降规律，Ⅰ、Ⅲ剖面桥面沉降增量比Ⅱ剖面大3 mm 左右，整体上桥面沉降差可忽略。

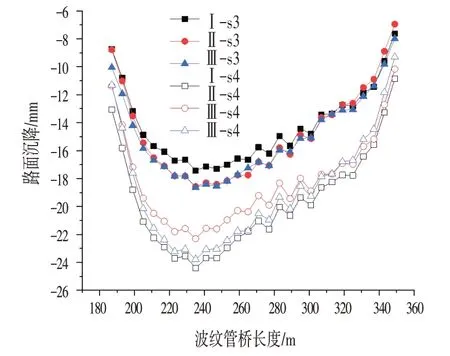
图8 桥面沉降Fig.8 Settlement of Road Surface

3.1.2 钢波纹管变形

从3.1.1 节知，拱桥两端基础竖向沉降最小、中部偏左基础竖向沉降最大，最终选取具有代表性的4号、12号管进行研究。

4号、12号钢波纹管拱顶、拱底竖向沉降曲线如图9所示，横坐标98～148 m 表示钢波纹管长度，T 表示拱顶测点，B 表示拱底测点（见图6）。从s2～s4 阶段钢波纹管沉降不断增加，4号、12号管拱顶总沉降量分别为20 mm、12 mm，s3 阶段沉降增量较大，说明管顶回填土产生的荷载比路面自重产生的荷载大，从s3阶段开始，管两端拱顶沉降比中间大。

图9 钢波纹管竖向位移Fig.9 Vertical Displacement of the Steel Corrugated Pipe

3.2 受力分析

文中主要对钢波纹管截面环向应力和绕管轴线弯矩的变化规律进行分析，选取了具有代表性的4号、12号管的剖面Ⅱ进行分析，测点位置如图7所示。

3.2.1 4号钢波纹管

4 号钢波纹管剖面Ⅱ的环向应力和弯矩如图10所示。随着施工不断进行，除管顶部区域，管周其他位置的环向应力呈不断增加趋势。变化最大的是管底部区域，较大值出现在管周0°、45°和315°处，其次是管周270°处（管腰）；随着管周填土不断回填，截面弯矩总体呈减小趋势，较大值出现在管周90°、180°、和270°处（管顶、管腰区域），其次是管周135°和225°（管顶左右区域），管周0°（管底）处弯矩几乎为0。弯矩的变化趋势与环形应力正好相反，s2 阶段弯矩最大，由于此时仅回填管周下半部分土体，大跨度钢结构侧向约束作用小，自重导致钢波纹管顶部竖向位移较大，导致管顶及管腰出现较大的弯矩。s3阶段回填上半部分土体，虽然侧向约束作用增强，但在覆土自重荷载作用下钢波纹管顶部弯矩仍然保持较大值；s3～s4 阶段期间，弯矩快速减小，可能是土体-结构协同变形使得结构受力变小。

图10 4号钢波纹管内力Fig.10 Internal Force of No.4 Steel Corrugated Pipe

3.2.2 12号钢波纹管

图11 为12 号钢波纹管剖面Ⅱ的环向应力和弯矩，环向应力及其变化趋势与4号钢波纹管基本一致，较大值出现在管周0°、45°、315°处（管底区域），最小环向应力出现在管周90°、135°、180°、225°和270°（管顶和管腰区域）；弯矩变化趋势与4 号钢波纹管不同，随着施工进行，弯矩几乎没有太大的变化，较大值出现在管周0°、90°、135°、180°、225°和270°处，即顶部、管底部和管腰处，最小弯矩出现在管周135°处。相比4号钢波纹管，12号钢波纹管底部出现了较大弯矩，可能是因为该钢波纹管的地基基础变形小、约束强，导致管底部出现反弯趋势。

图11 12号钢波纹管内力Fig.11 Internal Force of No.12 Steel Corrugated Pipe

4 结论

本研究以佛山市内的一座跨湖连拱桥为对象，通过数值分析研究了拱桥施工对地层变形、钢波纹管结构力学特性的影响及其规律，可以获得下列结论：

⑴拱桥施工阶段，基础和路面沉降比较均匀，工后基础表面和路面沉降最大值分别为30 mm、20 mm，均位于4～6 号钢波纹管位置处；回填上轻填土时基础沉降增量较大，钢波纹管变形较大，实际施工中应严格控制施工质量；

⑵钢波纹管南北两端管口处的顶部沉降比中部大，沿轴线方向钢波纹管顶部表现为微上凸，在施工中保护钢波纹管的稳定性时，应着重留意管口处，不至于施工导致结构产生较大变形；

⑶拱桥中部沉降较大的钢波纹管（如4、5 和6 号管），管底部区域主要受到轴力作用，管顶和管腰主要受到弯矩作用；拱桥两端沉降较小的钢波纹管（如1、2、11 和12 号管），管底区域主要受到轴力作用，管顶、管底和管腰主要受到弯矩作用；

⑷复合地基承载力大于设计承载力，可以较好地控制拱涵施工引起的地基基础沉降，从数值模拟的结果可知，计算结果满足软土地基处理工后一级公路沉降标准（一般路段≤0.30 m）。