斜拉桥索塔温度效应分析

徐 丰，周孟林，孟 康

武汉工程大学土木工程与建筑学院，湖北 武汉 430074

混凝土桥塔因本身高柔性以及安全因素的原因，结构需具有较高的强度、刚度、以及稳定性［1］。大跨径斜拉桥通常会受到强风、降雨以及太阳辐射的影响，其中强烈日照等非线性温度荷载会影响其合理线形、结构整体受力，从而对结构产生不利影响［2］。并且温度荷载使桥塔内部产生的温度次应力往往会超过其他荷载产生的应力［3］，同时桥塔各处也会产生变形。所以对桥塔的温度场及温度效应进行分析显得尤为重要。

程旭东［4］通过温度效应分析理论，计算了桥塔钢混结合段在夏季辐射最不利日照变化、寒潮来临、骤然降温等荷载作用下的温度效应，并对比了在日照温度作用下桥塔塔顶位移与斜拉桥监控中桥塔实测位移变形情况。陈定市等［5］推导出混凝土桥塔的热交换边界条件，并且通过编制热力耦合分析程序，算得桥塔在日照下的温度场和温度效应。杨吉新等［6］以某钢混桥塔为分析对象，得到骤然降温时桥塔的温度场及应力与变形，发现在骤然降温情况下，沿桥轴方向上桥塔内部会产生较大的温度梯度。刘诚诚等［7］通过分析高原地区薄壁空心高墩的温度次应力以及墩顶位移对该类桥墩的设计和施工提出合理建议。周浩等［8］使用经验模态分解法提取主梁主跨跨中受温度影响的挠度响应，得到了受温度影响的挠度响应。

1 工程背景

台州湾跨海大桥全长4.038 km，连接台州湾南、北两岸，北接临海，下承椒江，主桥是H 型桥塔双塔双索面叠合梁半漂浮体系斜拉桥，跨径布置为（85+145+488+145+85）m，采用双向6 车道高速公路标准，设计时速100 km。H型桥塔为高171.5 m的混凝土空心薄壁双肢筒状结构，每肢的截面为对称六边形。

1.1 桥塔温度场仿真模拟

1.1.1 初始条件 图1 为台州湾大桥桥塔示意图，本文对主梁施工前桥塔的温度场及温度效应进行分析。表1 列出了桥塔3 个特征截面的尺寸与位置参数。台州湾大桥的桥塔温度场受到太阳辐射、太阳方位角、大气气温和风速等诸多因素的影响［8-9］。将台州湾大桥所在地2017 年7 月29 日至2017 年8 月4 日实测的气象文件导入TAITherm 中计算，气象文件包含气温、云量、太阳辐射、风速的逐时数据。由于桥塔混凝土的水泥配合比相同且混凝土的截面面积远大于钢筋、裂缝和拉索面积，因此认为桥塔混凝土的材料是匀质的［10-11］。

图1 桥塔示意图Fig.1 Bridge tower diagram

表1 截面尺寸与位置参数Tab.1 Parameters of dimension and position of sections m

1.1.2 边界条件 当已知与物体边界接触的流体介质温度及换热系数时，边界条件可以表示为［10］：

其中：λ为混凝土导热系数，W/（m·℃）；h为热交换系数，W/（m2·℃）；t为介质温度，℃；tΓ为混凝土表面温度，℃。

混凝土桥塔的日照温度场模拟计算采用第三类边界条件，通过已知的混凝土表面温度和空气温度得到混凝土内部的对流系数，得到桥塔的边界条件，最后利用TAITherm 计算桥塔的温度场的时程。

2 桥塔温度场分析

2.1 内外表面温度变化规律

取2017 年7 月29 日 至2017 年8 月4 日 中 天 气晴朗、早晚温差大的8 月2 日的气象数据作为依据，对桥塔温度24 h 变化进行分析。

图2 为桥塔内外壁温度随时间变化图。在0～6 时，桥塔表面温度逐渐减小，变化与箱室外气温变化基本一致。随后，太阳光逐渐照射在桥塔东侧面时，东侧温度在10 时达到峰值（35.4 ℃）；南北两侧温度变化形式一致，在14 时达到最高温度；西侧在17 时，达到全天最高温度（38.4 ℃），而全天最高气温为22 ℃，两者相差16.4 ℃，说明太阳辐射是影响桥塔表面温度的主要因素。

图2 桥塔温度曲线：（a）外壁，（b）内壁Fig.2 Bridge tower temperature curves：（a）outer wall，（b）inner wall

桥塔内壁温度随时间逐渐增加，但由于内壁温度不受太阳辐射影响，所以内壁温度变化幅度不大，只有0.39 ℃。西侧和东侧内壁全天温度大于另外两侧，并且西内壁全天温度最高。

图3 为塔壁最大温差时温度分布图。由于台州湾大桥是南北走向，所以桥塔壁板最大温差出现东西两侧，经过计算发现东西两侧最不利温差出现在10 时和17 时。

图3 塔壁最大温差（单位：℃）：（a）10 时，（b）17 时Fig.3 Maximum temperature differences of bridge towerwall at 10 o'clock（a）and 17 o'clock（b）

2.2 径向温度变化规律

对不同时刻、不同截面下的混凝土箱型结构日照温度梯度的拟合公式为［11-13］：

其中，t(x)为测点温度（℃），A0为内外壁板温差（℃），a为指数系数。

对式（2）两边取对数得

通过最小二乘法，使实测值和拟合值差的平方和最小，由此计算出式（3）中的参数，得出径向温度分布梯度公式。

最后加上常数C得到径向测点温度，即

式中，C为测点内壁温度。

图4 为17 时特征截面沿径向温度梯度分布图。西侧17 时的温度为全天最高温度，在该温度下，沿径向方向温度随壁厚增加，呈指数函数形式下降。对比3 个不同壁厚的特征截面，当壁厚大于0.8 m 时，温差在0.1 ℃以内，可认为日照温度对桥塔径向温度的影响只在0.8 m 以内。并且当壁厚大于1 m 时，径向温度基本无变化，表明此时径向温度受日照辐射的影响微弱，与文献［14-16］结论一致。

图4 17：00 径向温度梯度Fig.4 Radial temperature gradients at 17：00 o'clock

图5 为2017 年8 月2 日至2017 年8 月4 日 东 侧和西侧最不利壁板温差下径向温度梯度拟合。对最不利壁板温差时刻进行指数函数拟合，发现指数函数能很好地模拟径向温度梯度，且函数相关性系数最小值为0.985。表2 为温度拟合参数表。

图5 径向温度分布模式Fig.5 Radial temperature distribution models

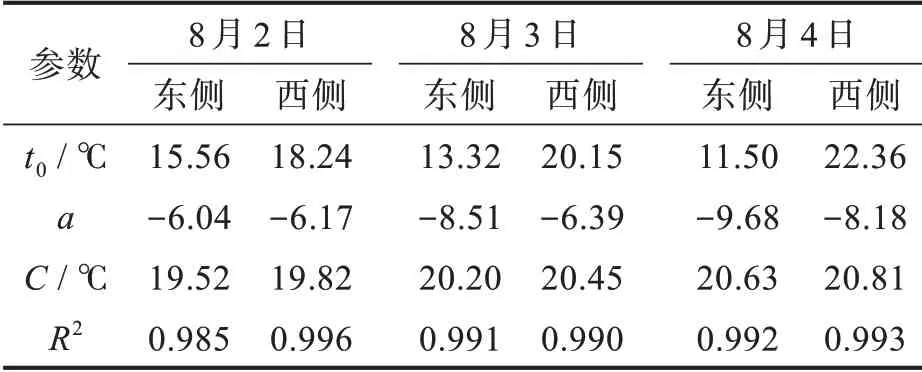
表2 径向温度拟合参数表Tab.2 Fitting parameters of radial temperature

3 桥塔温度效应分析

3.1 塔顶位移变化分析

将TAITherm 软件计算的桥塔温度数据导入MidasFEA 中，建立桥塔实体单元，施加节点温度荷载，进行三维温度荷载求解，得到桥塔特征界面的位移变化。通过分析桥塔的日位移变化，得到桥塔变形最大时刻。图6（a）为1-1 截面在横桥向、纵桥向以及竖向位移随时间变化图。随着温度的升高，横桥向位移缓慢增加，在10 时达到最大值（13.36 mm），然后随时间缓慢减小，在18 时达到最小值（4.49 mm）。纵桥向位移在6 时之前基本无变化，随着温度升高，在7 时达到1.37 mm。而之后随着太阳照射角度的变化纵桥向位移方向也产生变化，并在14 时达到最大值（4.30 mm）。竖向位移随时间变化缓慢升高，在17时达到最大值（21.93 mm）。由图6（a）可知，在无温度作用下横桥向位移和纵桥向位移分别为8.99 mm 和0.11 mm，横桥向位移相较于纵桥向位移对温度变化更敏感，变化更大。

图6 位移变化曲线：（a）1-1 截面，（b）特征截面Fig.6 Displacement variation curves：（a）1-1 section，（b）characteristic sections

图6（b）为特征截面总位移随时间变化图。当桥塔的高度增加时，截面的位移也随之增加，并且高度低的截面位移基本呈一条直线。随着高度的增加，位移曲线中间开始产生凸起，高度越高，位移变化的差值越大，在1-1 截面变化值达到4.33 mm，而在3-3 截面只有0.16 mm。在0 时至6 时基本不变，6 时至10 时开始增加，10 时至18 时减小，最终趋于平稳。

图7 为特征截面沿径向方向位移曲线变化。1-1 截面的位移在距外壁0.1 m 处减小并随后逐渐增大，呈正勾状。而处于桥塔横梁下的2-2 和3-3截面位移在距外壁0.1 m 处增大随后逐渐减小，呈倒勾状，与1-1 截面趋势相反，说明桥塔中的横梁会改变截面的径向位移的变化趋势。

图7 特征截面径向位移变化Fig.7 Variations of radial displacement of characteristic section

3.2 桥塔应力分布分析

基于平截面假定，当桥塔受到不均匀温度场时会产生温度次应力。图8 为桥塔特征截面外缘应力随时间变化曲线。由图8 可知，越靠近塔底，塔壁越厚，外缘竖向应力就越大，最大值为7.3 MPa。并且外缘竖向应力随温度变化，温度越低，应力越小，温度越高，应力越大。在全天温度最低的6 时左右达到最小值，在温度最高的17 时达到最大值。

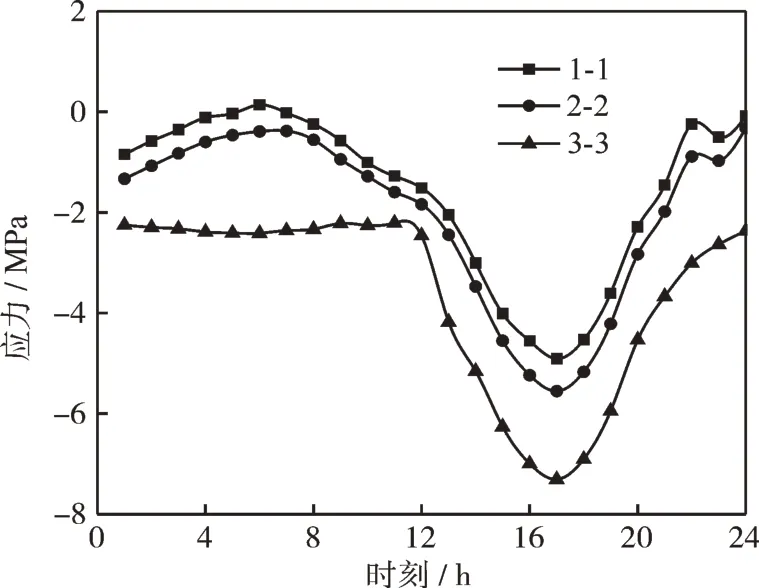
图8 桥塔外缘竖向应力变化Fig.8 Vertical stress variations at outer edge of bridge tower

图9 为桥塔沿径向方向应力变化曲线。通过对桥塔径向应力分析，发现竖向应力的全天变化曲线呈漩涡状。在1 时，截面内的竖向应力为正勾性，随着温度的降低，外缘应力为压应力并逐渐减小，在气温最低的6 时外援应力达到全天最小值。随后随着温度的增加，外缘应力逐渐增大，在17 时达到最大值，随后又逐渐减小。外缘应力与0.1 m处应力的变化形成整个图形的漩涡口，在距离外壁0.2 m 处的应力对温变的敏感性逐渐降低。靠近内壁时，应力逐渐由压应力变成拉应力。

图9 桥塔径向应力变化：（a）1-1，（b）2-2Fig.9 Radial stress variations of bridge tower：（a）1-1，（b）2-2

4 结 论

（1）桥塔表面温度与大气温度相差较大，说明太阳辐射是桥塔表面温度的决定性因素。桥塔内壁温度不随太阳辐射变化，只受大气温度和对流辐射影响，会随时间和高度逐渐增加。桥塔径向方向温度梯度符合负指数函数t(x) =A0e-ax+C，且证明该公式的精度。

（2）桥塔总位移变化主要受到横桥向位移变化影响，且对比无温度下位移发现横桥向位移相较于纵桥向位移对温度更敏感。当高度增加时，桥塔的位移增加，位移变化的差值也增加。桥塔截面的径向位移呈勾状，塔顶的径向位移为正勾状，而处于横梁下的截面呈现倒勾状，说明横梁会改变径向位移的变化趋势。

（3）桥塔外缘竖向应力随高度增加而减小，在温度较低时应力较小，温度较高时会朝压应力方向增大。沿截面方向的全天应力图呈现漩涡状，桥塔表面到0.2 m 处的应力更容易受到温度影响。随着深度增加，应力有从压应力变为拉应力的趋势。