考虑轴力和剪切效应的盾构隧道纵向变形分析

杨成永 ，马文辉 ，费 腾 ，韩薛果 ，程 霖

（北京交通大学土木建筑工程学院，北京 100044）

盾构隧道、地下管线等地埋构件一般采用弹性地基梁的方法分析其变形和内力.但盾构隧道与其他地埋构件相比，有两个不同点：一是盾构隧道由于其圆环的截面形式及环缝的存在，其剪切刚度比弯曲刚度小很多，因此剪切变形不可忽略；二是盾构隧道在修建时，为了环间防水的需要，环缝被挤紧，存在轴向受压的装配力[1].本文探究了在剪切变形及轴向荷载影响下盾构隧道纵向变形的计算方法及纵向变形的规律.

剪切变形可采用Timoshenko梁理论进行处理.隧道在横向力作用下将产生弯曲变形wb(x) 和剪切变形ws(x) ，总变形w(x) 为两者之和[2].

Timoshenko梁理论认为，剪切变形只是使梁产生挠度，不产生内力；弯曲变形和剪切变形分别满足不同的微分方程；弯曲变形和剪切变形需要分开进行计算.

Wu等[3-4]考虑剪切效应探讨了盾构隧道的变形问题.他们的方法是按总变形建立控制微分方程.这样做需要对剪切变形（挠度）求高于二阶的导数.由于剪切变形的二阶导数是荷载集度，其三阶及四阶导数缺乏明确的物理意义.另外，当隧道不是无限长而是有限长时，端部条件需要同时满足弯曲变形和剪切变形的要求.

Hetenyi[5]研究过梁在其端部承受轴向拉力的情况，杨成永等[6]探讨了挠曲变形产生的轴力对地下管线变形的影响.他们处理轴力的方法均是在控制微分方程中增加了轴力项，并且得到的微分方程是一致的.在小变形情况下，挠曲变形轴力可以忽略.

本文分别列出了弯曲变形和剪切变形遵从的微分方程，讨论了右端荷载的形式，然后考虑剪切变形所产生的那部分地基反力，建立了弯曲变形的控制微分方程.按照剪力的表达式，推导了剪切变形的计算公式；采用带补充项的傅立叶级数为弯曲变形的展开式，得到了求解弯曲变形傅立叶系数及端部转角和剪力的方程组.给出了求解挠曲变形轴力的迭代步骤.通过本文的傅立叶解与既有理论解的对比，验证了级数解的正确性.最后采用本文方法计算分析了盾构隧道纵向变形的规律.

1 隧道变形的控制微分方程

1.1 基本方程

1.1.1 弯曲变形

考虑轴力的弹性地基梁的弯曲变形挠曲线微分方程[5-6]为

式中：E为隧道的弹性模量，kPa；I为隧道横截面的惯性矩，m4；wb(x)为弯曲变形量；D为隧道的外径，m；K为地基系数，kPa/m；q(x)为作用在隧道上的分布荷载（不包含地基反力），kPa，向上为正；Na为盾构隧道由于装配产生的轴力，kN，轴力以拉为正；Nd为由于隧道挠曲变形产生的轴力，kN；x为沿隧道轴线的坐标（中点处x= 0），m.

根据弯曲变形计算弯矩M（x）及剪力Q（x），分别如式（2）、（3）.

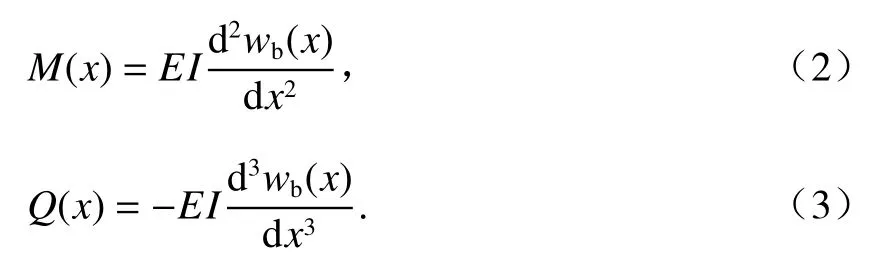
1.1.2 剪切变形

弹性地基梁的剪切变形遵从的挠曲线微分方程[2]为

式中：η为Timoshenko梁的剪切系数；G为隧道的剪切模量，kPa；A为隧道的截面面积，m2；ws(x)为剪切变形.

不同类型截面Timoshenko梁的剪切系数[7-8]为

式中：m=d/D，d为圆环内径，m；v为泊松比.

由式（4）可得剪切变形为

1.2 右端荷载

盾构隧道主要承受由于地层不均匀、地层固结或近接施工产生的土层位移荷载，但为了本文方法具有更广泛的实用性，还考虑隧道承受满布均布荷载、对称的集中力及对称的局部均布荷载作用，如图1.图中：x0为集中力P作用的位置；x1为局部均布荷载的起始位置；c为局部均布荷载的分布宽度；S0为土层在沉降槽中点处（x= 0）的最大沉降，向上为正；i为土层沉降槽半宽，即沉降曲线反弯点距x=0处的水平距离；L为计算范围的半宽.则式（1）中的右端荷载可写为

图1 盾构隧道上的作用荷载及其沉降示意Fig.1 Schematic of loads on a shield tunnel and its deflection

式中：S(x)为土层沉降，m，向上为正；q0为满布均布荷载，kN/m；q1为局部均布荷载，kN/m；荷载均以向上为正.

式（7）中集中力有两个，局部均布力有两处，均呈对称分布.

为了进行级数法求解，需要在式（7）中引入脉冲函数和阶梯函数，如式(8).

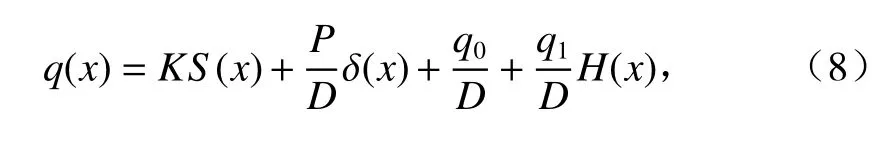
式中：δ(x)为脉冲函数，如式（9）；H(x)为 Heaviside阶梯函数，如式（10）.

由式（9）和式（10）可知：当令x0= 0 时，可得到作用在沉降槽中央的大小为2P的集中荷载；当令x1= 0时，就得到作用在沉降槽中央的分布范围为2c的局部均布荷载.

式（8）中的土层沉降一般服从正态曲线，即

当土层位移荷载、集中荷载和局部均布荷载不对称时，计算公式将有不同，但不存在数学困难.

1.3 考虑剪切变形影响的控制微分方程

在存在有弹性地基时，剪切变形将产生相应的地基反力.考虑剪切变形引起的地基反力后，式（1）中右端荷载将增加一项 -KDws(x)，负号表示地基反力与隧道剪切变形的方向相反.结合式（1）和式（6）得式（12）.

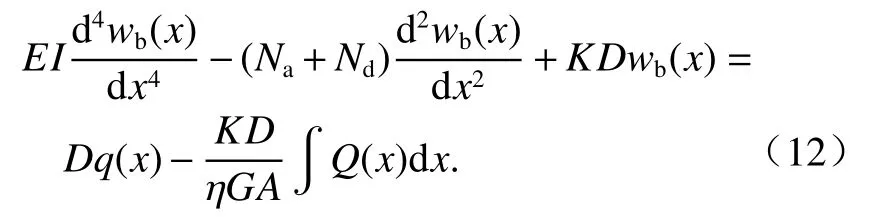
将式（3）代入式（12）中的积分项，将式（8）代入式（12）中的右端第一项，得考虑轴力和剪切变形影响的弹性地基上盾构隧道的弯曲变形的挠曲线微分方程为

2 傅立叶级数求解

2.1 函数的级数展式

为了使问题得到简化，将式（13）中的Nd作为一个待求的常量，即用平均轴力（Ndmean）代替Nd.为了对式（13）进行级数求解，需要把式（13）和式（8）中的wb(x)、S(x)、δ(x)、H(x)展开成三角傅立叶级数.由于对称，可分别展成余弦级数.

为了能同时适应有限长隧道和无限长隧道两种情况，wb(x)的级数展开采用在范围[-L，L]上的带补充项的余弦傅立叶级数[9]为

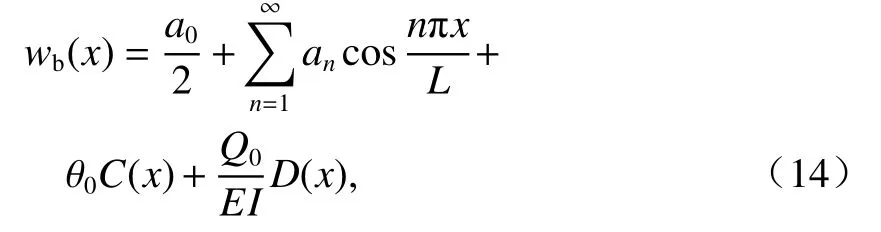
式中：a0～an均为待求的傅立叶级数系数；θ0为隧道两端的转角，rad；Q0为隧道两端处的剪力，kN；an、θ0和Q0均是待求量；C(x)、D(x)分别如式（15）、（16）.

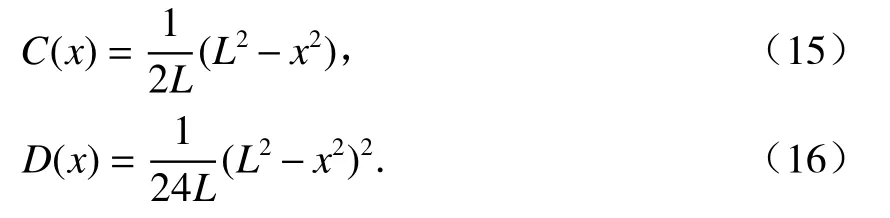
当θ0和Q0均为 0 时，对应无限长隧道的情况，此时式（14）已满足两端转角为0及剪力为0的边界条件，并且由于对称，中点的转角及剪力也为0；当θ0或Q0不为 0时，对应有限长隧道的情况；θ0为0而Q0不为0时，对应两端固支的情况；θ0不为0而Q0为0时，对应两端自由的情况；θ0及Q0均不为0时，对应两端简支的情况.

级数求解中补充项也需要展开成余弦傅立叶级数.

C(x)的级数展开为

D(x)的级数展开为

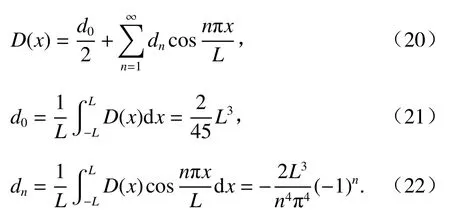
式（14）按C(x)和D(x)的级数展开式得到的各阶导数为

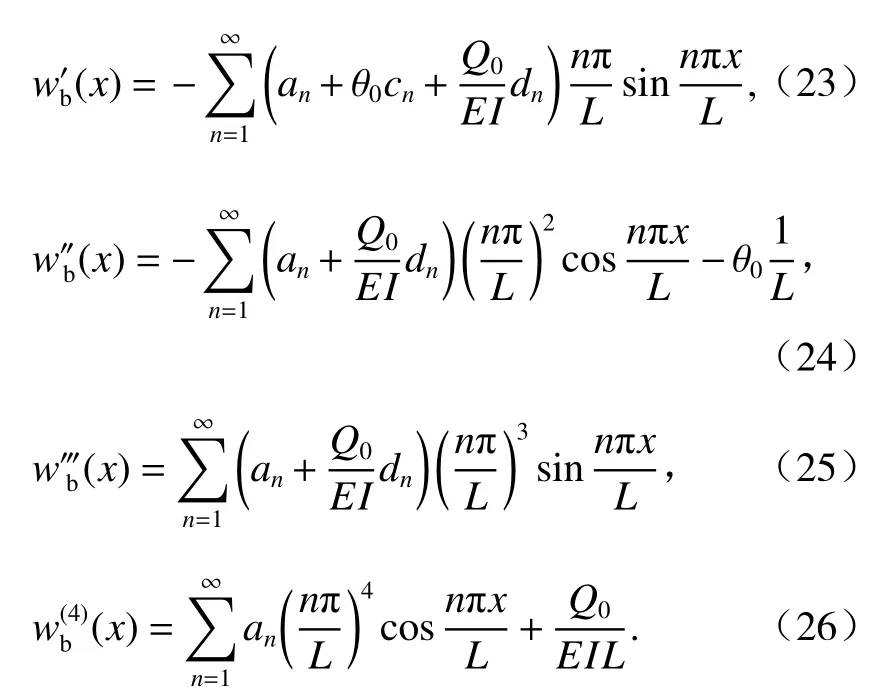
S(x) 在[-L，L]上的余弦傅立叶级数展开为

式中：s0和sn均为S（x）的傅立叶级数系数.

在计算范围较大，如L取不小于3i时，利用式（11）有

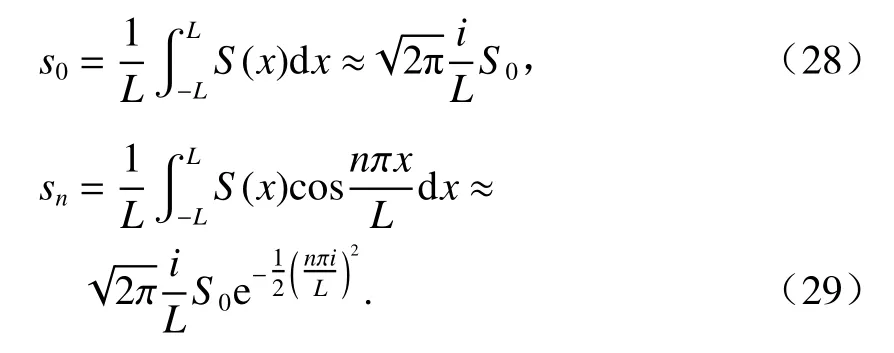
若梁的长度较短，并在该短梁上要施加土层荷载，则式（28）、（29）只能采用直接积分的方法计算.

δ(x)的傅立叶级数展开[9]为

H(x)的傅立叶级数展开为

2.2 剪切变形的计算公式

将式（15）、（16）代入式（14），求三阶导数后代入式（3），再代入式（6），得

2.3 方程组及相关变量计算

将式（17）、（20）代入式（14），然后把式（14）、式（24）、（26）、（27）、（30）、（33）代入式（13），比较常数项及三角函数的系数，得到求解式（14）中级数系数及待求量的方程组为

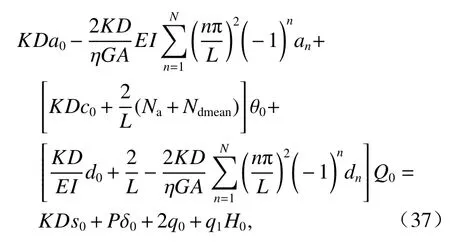
式（37）、（38）中有N+1个方程，N+4个未知量：a0及an、端部转角θ0及剪力Q0、平均挠曲变形轴力Ndmean.

对端部转角θ0，当为无限长隧道和两端固支的有限长隧道，θ0= 0；对两端简支或自由的有限长隧道，可利用隧道端部弯矩为0的条件增加一个补充方程.将式（15）、（16）代入式（14）并求二阶导数，令其在x= ±L处等于 0，有

对端部剪力Q0，当为无限长隧道和两端自由的有限长隧道，Q0= 0；对两端简支或固支的有限长隧道，可根据端部位移为0的条件来增加另一个补充方程.令式（14）在x= ±L处等于 0，有

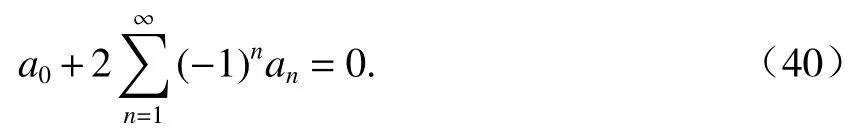
Ndmean需要采用迭代法进行计算.

2.4 挠曲变形轴力的迭代过程

式（37）、（38）中未知量Ndmean的迭代过程如下：

1）按式（18）、（19）计算c0和cn，按式（21）、式（22）计算d0和dn，按式（28）、（29）计算s0和sn，按式（31）、（32）计算δ0和δn，按式（34）、（35）计算H0和Hn.

3）根据不同类型的梁及梁的不同支承条件，按式（37）、（38）、（39）、（40）组成方程组计算a0、an及θ0和Q0.

4）根据a0、an、θ0和Q0按式（14）通过数值积分计算梁的半弧长L(j)，然后计算挠曲变形产生的平均轴力为

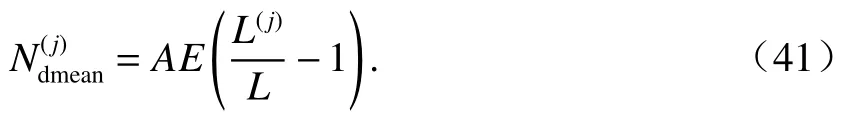
6）按式（14）计算弯曲变形产生的挠度.按式（36）计算剪切变形产生的挠度；两者相加得总挠度.

7）按式（2）计算弯矩M（x）；按式（3）计算剪力Q（x）.

其中关于挠度w（x）的二阶及三阶导数可以分别按式（24）、（25）计算，也可按式（42）、（43）计算.

至此，若与隧道有关的参数D、d、E、v、G，以及与荷载有关的参数K、S0、i、P、q0、q1已知，则可计算隧道的沉降和内力.

不难理解，上述的级数解力学模型可以进行多种情况的简化：若不考虑剪切变形，则在前述的公式中去掉包含的项；若不考虑装配轴力，则去掉包含Na的项；若不考虑挠曲变形轴力，则去掉包含Nd及Ndmean的项，求解过程也无需进行迭代；若没有土层位移荷载、集中力或均布荷载，则分别去掉包含S0及b0和bn、P、q0、q1的项.若不考虑弹性地基，则去掉包含K及KD的项.

3 计算与分析

3.1 计算数据

后续计算中用到的关于盾构隧道、土层及荷载的计算参数如下：

盾构隧道L= 62 m，D= 6.2 m；无限长梁时，取L= 2.5 × 62 m，等效抗弯刚度EI= 8 × 107kN·m2，等效抗剪刚度ηGA= 4 × 106N，K= 1 000 kPa/m；P=-1 000 kN （x0= 0）；q0= -50 kN/m；q1= -100 kN/m，分布范围 10 m （x1= 0，c= 5 m）；Na= -20 MN.

土层位移荷载取土层沉降参数：最大沉降S0=-10 mm，沉降槽半宽i= 6 m.

计算中级数取200项.后面第3.2节～3.4节中，未特别指明的参数，均采用本节所列数值.

3.2 模型验证

采用普通梁及弹性地基梁的解析解来验证本文级数解的正确性.

选取无弹性地基和有弹性地基各4个算例进行计算，分别列于表1、2.表中：Mc、wc分别为中点弯矩及挠度；wd为端点挠度.

表1 无弹性地基时解析解与傅立叶级数解的计算结果Tab.1 Analytical and Fourier series solutions for an ordinary beam

从表1和表2的对比计算可以看出：

表2 有弹性地基时解析解与傅立叶级数解的计算结果Tab.2 Analytical and Fourier series solutions for a beam on elastic foundation

1）级数解在有无弹性地基、考虑和不考虑剪切变形及轴力各种情况下，均与理论解吻合很好.

2）级数解与理论解，在满布均布荷载时，计算结果完全相同；在局部均布荷载时，前四位有效数字相同；在集中荷载时，区别最大，最大相对误差发生在例7的弯矩，为1.03%.造成局部均布荷载及集中荷载时有差异的原因是采用阶梯函数及脉冲函数来模拟荷载分布形式的缘故.

3.3 盾构隧道剪切变形占总变形的比例

盾构隧道剪切变形的大小与其截面形式、端承条件、荷载形式、长高比以及有无弹性地基有关.

3.3.1 截面形式

关于截面形式对剪切变形的影响，可根据式（5）的剪切系数及表1中Timoshenko梁的挠度式进行对比计算.不考虑弹性地基，也不考虑环缝的存在.隧道的抗弯刚度及剪切刚度根据截面尺寸和弹性模量与剪切模量进行计算.取隧道内径d= 5.5 m；E=3.45 × 107kPa，v= 0.2，其他参数（l、D、P及q0）仍按第3.1节中取值，结果见表3.

表3 截面形式对比计算结果Tab.3 Comparison between circular and annular cross sections

由表3可以看出：具有空心圆环断面的盾构隧道，即使不考虑环缝的存在，其剪切变形占总变形的比例也比实心梁构件大许多；圆环截面算例2是圆截面算例1的2.9倍，算例4是算例3的2.6倍.

3.3.2 端承条件、荷载形式及长高比

盾构隧道实为弹性地基构件并主要承受土层位移荷载.为分析端承条件、荷载形式及长高比情况下盾构隧道剪切变形的大小，按不同支承条件（两端自由、两端简支、两端固支、无限长梁）、不同荷载形式（满布均布荷载、集中荷载、土层位移荷载）及不同长高比（10∶1、20∶1、30∶1）计算隧道的弯曲变形和剪切变形.长高比10∶1是按约10倍的沉降槽半宽确定的；长高比20∶1、30∶1是用于考查随计算范围的扩大，有限长隧道的计算结果与无限长隧道间的差异.具体的计算结果列于表4.

从表4可以看出：

1）不同支承条件间进行比较可知，两端固支时剪切变形在总变形中的占比最大，其他支承条件（两端自由、两端简支、无限长隧道）时该占比小并且较为接近.

2）不同荷载形式间进行比较可知，对两端自由、两端简支、无限长隧道，荷载在跨中的集中度越大剪切变形的占比越高.

但在两端固支时，集中荷载和满布均布荷载时剪切变形的占比较大并且两者数值接近；在中部有局部荷载（正态分布的土层位移荷载）时，剪切变形的占比较小.这一现象在无弹性地基时也是如此.因此，这个规律是由端部条件决定的.

3）长高比越小，剪切变形在总变形中的占比越大[2].从表4对集中荷载的计算结果来看，对两端自由、两端简支隧道，当长高比大于10后，剪切变形的占比趋于稳定，与无限长隧道接近.对两端固支隧道，这一比值约为15.

3.3.3 有无弹性地基

用表1中的变形数据计算剪切变形与总变形之比，列于表5.

比较表4与表5中对应的数据可知：当有弹性地基时，弯曲变形及剪切变形均明显减小.但剪切变形与总变形的比例并没有趋势性的变化.

表4 盾构隧道弯曲变形和剪切变形的计算结果Tab.4 Bending and shear deformations of shield tunnels

表5 无弹性地基时弯曲变形和剪切变形的计算结果Tab.5 Bending and shear deformations of a shield tunnel as an ordinary beam without elastic foundation

3.4 剪切刚度对变形和内力的影响

针对无限长弹性地基隧道进行计算.参照文献[4]中外径6.2 m和11.0 m盾构隧道的等效抗剪刚度分别为 2.08 × 109N 和 3.38 × 109N，本次计算的等效抗剪刚度变化范围取为ηGA= 8 × 109，4 × 109，2 ×109，1 × 109N.其他参数按第 3.1 节中取值.计算隧道在土层位移荷载作用下的沉降和弯矩.结果列于表6.

表6 盾构隧道剪切刚度对变形影响的计算结果Tab.6 Influence of shear rigidity of a shield tunnel on its deformation

从表6可知弯曲变形和剪切变形呈现如下规律：

1）考虑剪切变形后，总挠度是增加的；

2）随剪切刚度的降低，剪切挠度增大，其在总挠度中的占比也增大，该占比可以达到20%以上；

3）虽然总挠度是增加的，但随剪切刚度的降低，弯曲挠度及弯矩是减小的，产生这一现象的原因，是由于剪切变形所对应的那部分地基反力，抵消了部分外荷载所致.

3.5 装配力对弯曲变形和弯曲内力的影响

对无限长盾构隧道，参照文献[1]对盾构隧道管片纵向应力的测量结果，取Na= -10，-20，-40 MN.其他参数仍按第 3.1 节中取值.计算隧道在土层位移荷载及轴力作用下的沉降和弯矩.结果列于表7.

表7 盾构隧道装配轴力对变形影响的计算结果Tab.7 Influence of installation caused axial force of a shield tunnel on its deformation

由表7可知：1）随轴力的增大，挠度和弯矩均增大；2）轴力对挠度和弯矩的影响幅度不大，一般对挠度的影响不超过2%，对弯矩的影响不超过3%.

4 结束语

本文把弯曲变形和剪切变形分开分别计算.弯曲变形和剪切变形两者的联系是在有弹性地基时，在弯曲变形的挠曲线微分方程中需要考虑剪切变形产生的地基反力.剪切变形的计算可以采用两种方法：一是通过外部荷载（包括地基反力）；二是通过内力（剪力）.本文采用的是较为简单的内力的方式.

得到如下主要结论：

1）考虑剪切变形后，总挠度有所增加，但弯曲挠度及弯矩反而有所减小.

2）剪切变形随剪切刚度的降低而增大.

3）剪切变形占总变形最少可达20%.这么大的剪切变形一是由截面形式（圆环截面）贡献的，二是由低的剪切刚度造成的.这里要注意，如果环缝的存在引起抗弯刚度和抗剪刚度同等幅度地降低，是不会增大剪切变形的占比的.

4）盾构隧道所受的轴向力对其竖向挠度和弯矩的影响较小，可以忽略.

本文所建立的计算方法适应于长隧道和短隧道、有弹性地基和无弹性地基，并可考虑多种荷载形式.但所讨论的问题是对称的，对非对称问题，可采用不同的补充项及正弦级数展开解决，公式要复杂一些，但不存在数学困难.