含EVs的交直流混合微电网两阶段鲁棒调度优化

李 奇 ，黄兰佳 ，邱宜彬 ，孙 彩 ，傅王璇 ，陈维荣

（西南交通大学电气工程学院，四川 成都 610031）

随着能源危机和环境污染的日益加剧以及新能源并网技术的发展，微电网作为可再生分布式电源发展的重要手段已成为了近年来各国的研究重点[1-2]，国家的节能减排政策也使得电动汽车（electric vehicles，EVs）得到发展和普及，电动汽车数量逐年增加.然而，电动汽车运行特性与用户出行习惯相关，其大规模分散地接入电网中会产生大量随机负荷，加大负荷的峰谷差，影响电能质量[3].若考虑电动汽车运行时的源荷双重特性，将其接入微电网中，有序进行充放电管理，能够有效解决该问题，并为微电网带来可观的经济效益，实现双赢.近年来，有关电动汽车接入微电网的系统运行研究受到广泛关注.

微电网中诸如风电、光伏发电出力的准确预测尤为困难，用户的负荷需求也存在着一定的波动，电动汽车无序的运行方式也会带来较大的随机负荷，上述的不确定因素都为微电网的调度带来了挑战.对于此类不确定问题，现有的研究方法主要有随机规划和鲁棒优化.随机规划通过对随机变量概率分布大量采样获得典型场景来描述随机变量的不确定性[4-5].该方法随着采样场景的增多，求解规模呈指数型扩大，求解过程繁琐复杂[6]，其概率论的数学本质也使得优化所得方案只能为其可行性提供概率保证，并不能可靠地应对所有的不确定性.鲁棒优化则通过寻找随机变量可能取值构成的不确定区间内的最恶劣场景，并针对该场景进行优化，得到相应的调度方案.该方法优化过程无需考虑变量的具体概率分布，计算简单，所得方案具有强鲁棒性，能够应对不确定集合中的任意场景，因此，近年来该方法备受研究者青睐.文献[7]针对系统中的不确定性建立了min-max-min两阶段鲁棒模型，经过一系列转化和推导，将模型转化为混合整数线性规划模型以求解最恶劣场景下的最优解.文献[8]采用鲁棒优化方法考虑了孤岛交直流微电网中各微源出力、负荷以及双向换流器状态的不确定性，提出了区间不确定性约束鲁棒调度模型.文献[9]针对并网型微电网，考虑交直流混合微电网系统中的不确定性，提出了一种双层两阶段鲁棒调度模型.

在电动汽车与微电网的调度方面，国内外学者也做了大量研究.文献[10]为实现EVs与电网的有效交互，结合EVs充电站的建设，建立了基于粒子群优化算法的充放电模型.文献[11]针对EVs能量的双向流动性，提出了包含风、光、储、EVs等的微电网经济调度策略和模型.文献[12]建立了计及电动汽车充放电的微电网分级调度模型，分成负荷级及源荷级进行优化，得出了各级的最优调度策略，有效地利用EVs进行负荷转移.但上述文献并未充分考虑系统中诸多的不确定因素.文献[13]针对微网中不确定因素，建立了极端场景集下的含电动汽车的鲁棒调度模型，通过评估系统弃光和弃负荷成本，提出风险成本模型，综合考虑方案的经济性与运行可靠性.文献[14]考虑电动汽车负荷需求的用电方案，将风电运行成本和电动汽车充电成本函数进行加权，将鲁棒问题转换为鲁棒随机最短路径问题进行求解.文献[15]利用鲁棒优化对含电动汽车与可再生能源的微网系统协同优化进行建模，调度电动汽车有序充电实现系统削峰填谷，消纳可再生能源目的，但其所使用的鲁棒优化方法依然具有“过度保守”问题.

近年来，交直流混合微电网以其能够兼容交直流负荷，促进风光能源的互补利用，提高新能源利用率和微电网运行效率的优点得到了研究者的重视[16].本文为探讨含电动汽车的交直流混合微电网日前优化调度问题，建立了含电动汽车充放电的交直流混合微电网两阶段鲁棒调度模型.鲁棒调度最忌模型保守性，本文建立模型时，采用盒式不确定集描述不确定性，引入不确定预算灵活调节模型的保守性，通过强对偶理论及BIG-M法，将模型转换为混合整数线性规划模型，最后采用列约束生成算法（column and constraint generation algorithm，C&CG）进行求解.结合算例对电动汽车接入微电网的影响进行分析，得出了当前算例下的电动汽车最优接入辆数，而后，基于最优接入辆数分析了模型的经济性与可行性.

1 含EVs的交直流混合微电网系统结构描述

本文研究对象含EVs交直流混合微电网系统结构如图1.图中，风力发电单元、微型燃气轮机和交流负荷连接至交流母线构成交流供电区域，光伏发电单元、储能、电动汽车及直流负荷连接至直流母线构成直流供电区域.交流供电区域可通过公共连接（point of common coupling，PCC）节点连接至配电网，进行功率交互.双向AC/DC换流器与交流母线和直流母线连接，两区域可通过换流器进行功率交互.该系统主要包含以下运行特点：

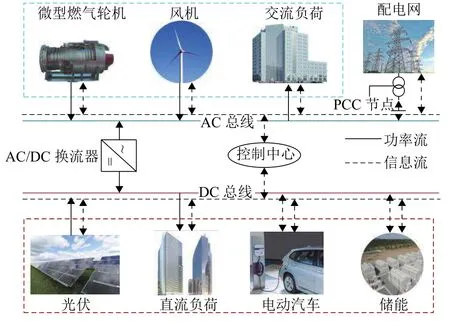
图1 含电动汽车的交直流混合微电网模型Fig.1 AC-DC hybrid microgrid model with electric vehicles

1）系统分为交流区域和直流区域，各区域主要通过分布式发电为区域内的负荷供电.区域间通过AC/DC双向换流器进行功率交换，实现区域内部电能的供需平衡.

2）电动汽车用户可通过与微电网签订协议，在满足自己出行需求的条件下参与调度，获取需求响应收益.本文对电动汽车采取集中调度的方式，电动汽车的购置成本由用户承担.

3）储能单元权属于微电网，在调度过程中，蓄电池和作为动态储能的电动汽车的联合充放电完成负荷需求响应，实现电量存储和负荷的削峰填谷，最大限度地利用可再生能源.

4）当系统内部电量供需不足时，微电网可通过PCC节点向配电网购电以维持功率平衡.反之，当系统在满足内部负荷需求还有富余时，可向配电网售电以赚取收益，降低系统的运行成本.

2 交直流混合微电网日前鲁棒调度模型

2.1 目标函数

综合考虑系统的运维成本、联络线交互成本、燃料成本、储能损耗成本以及电动汽车的补贴成本，所建立的目标函数为

式中：COM为包含风机、光伏、换流器以及微型燃气轮机单元的运维费用，如式（2）；Cgrid为系统向配电网的购售电成本，如式（3）；Cfuel为微型燃气轮机的燃料成本，如式（4）；CES为储能单元调度的损耗成本，如式（5）；CEV为微电网对电动汽车用户配合调度的补贴，如式（6）.

式（2）～（6）中： Δt为调度步长，本文取值为 1 h；t为时段；T为调度周期，本文取值为 24 h；mWT、mPV、mBC、mMT分别为风机（WT）、光伏（PV）、换流器和微型燃气轮机的运维系数；PWT，t、PPV，t、PMT，t分别为时段t风机、光伏和微型燃气轮机的出力；（）为时段t经换流器由交（直）流侧转换至直（交）流侧的功率；λt为微电网在调度各时段日前交易电价；为微电网在时段t向配电网的购（售）电量；aMT为燃料成本系数；mES为考虑蓄电池损耗的静态储能调度成本系数；为蓄电池的充（放）电效率；为储能在时段t的充（放）电功率；为时段t第i辆电动汽车对微电网的充（放）电功率；I为电动汽车辆数；mEV为微电网对电动汽车配合调度的补贴成本系数.

考虑电动汽车充放电损耗，mEV可由式（7）估算得出[13].

式中：mBat为电动汽车电池购买成本；EEV为电池容量；LDoD为放电深度；Nc为在放电深度为LDoD下电池的循环次数.

2.2 约束条件

交直流混合微电网的日前鲁棒调度模型需要满足以下约束条件.

1）微源出力约束

微型燃气轮机的出力（PMT,t）需在最大和最小出力之间，如式（8）.

2）储能单元约束

储能的充放电功率约束为

储能单元还需满足容量约束，如式(10)、(11).

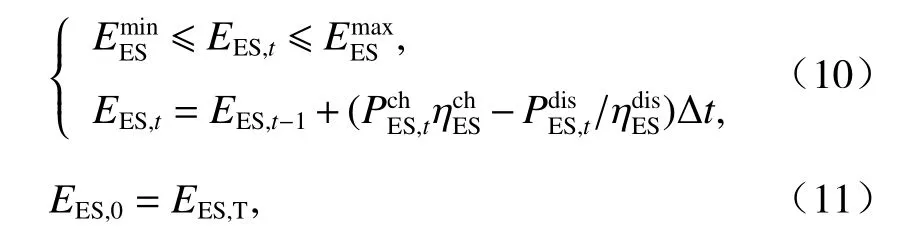
3）换流器运行约束

运行时换流器应满足换流功率约束和换流状态约束，如式(12).

由于换流器功率波动较大时会对电能质量造成影响，需对换流器相邻时段换流功率波动进行约束，如式(13).

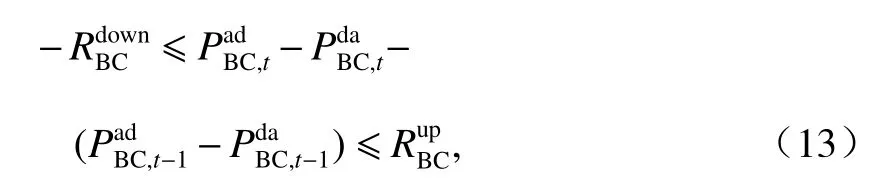
4）配网功率交互约束

与配电网的功率交互需满足式（14）约束.

5）EVs约束

EVs参与微电网调度需在式（15）约束下进行.

调度过程中，考虑动力电池的使用寿命问题，EVs容量EEVi,t需在最大和最小容量之间，如式（16）.

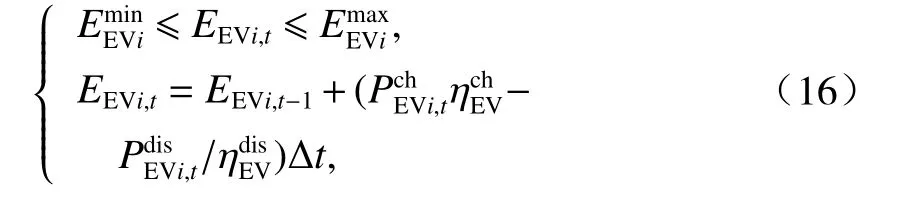
用户出行时，动力电池应处于最大容量状态，应满足式（17）约束.

此外，电动汽车需在满足自身出行电量下参与调度，故其放电量应当满足式（18）约束.

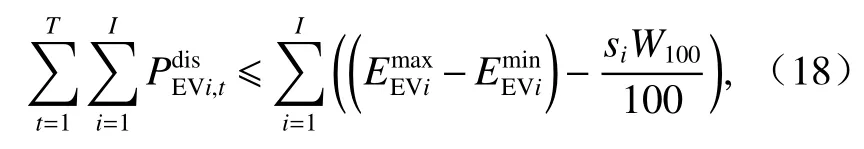
式中：si为第i辆电动汽车的日出行里程；W100为电动汽车行驶100 km所需电量.

6）系统功率平衡约束

调度过程中，系统应保持交流区域和直流区域的功率平衡，即

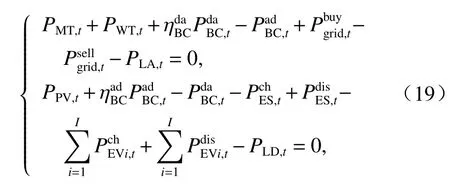
2.3 不确定集

本文研究过程中所涉及的不确定变量包括交流侧的风机出力、交流负荷、直流侧的光伏出力以及直流负荷，设不确定集W中的元素为wj，则对于变量wj在时段t的区间估计为

盒式不确定集在描述不确定性时，会为调度带来严重的保守性，由中心极限定理[17]，实际运行中不太可能发生所有变量同时达到边界的情况，故此引入不确定性预算约束，改善不确定集的保守性，引入不确定性预算约束后的盒式不确定集合表示形式为

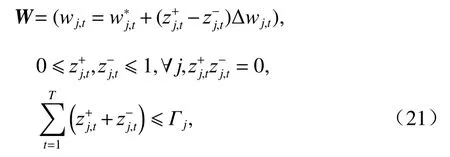
式中：Γj为不确定预算.

由式（21）可知：Γj取值越大，优化过程中考虑的不确定性就越多，优化所得调度方案就越保守，相反则越为冒险；当取值为0时，表明实际运行情况与预测场景没有偏差，不确定性优化随即转变为确定性优化.

2.4 两阶段鲁棒优化模型

将上述目标函数和约束条件进行整理，所得两阶段鲁棒优化模型的矩阵形式为

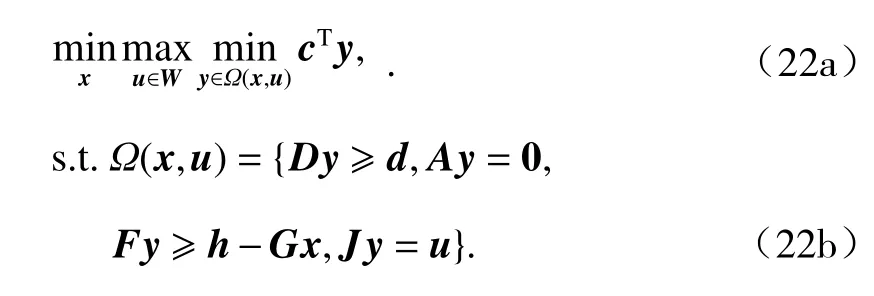
式中：x、y分别为第一阶段决策的二进制状态变量和第二阶段决策的输出变量，如式（23）；u= （wWT，t，wPV，t，wLA，t，wLD，t）T为第二阶段不确定变量构成的不确定场景；Ω（x，u）为给定x、u下y的可行域.

式（22a）对应式（1）～（6）的目标函数，Dy ≥d对应的约束为式（8）、（11）、（13）、（16），Ay= 0 对应的约束为式（11）、（19），Fy ≥ h-Gx对应的约束为式（9）、（12）、式（14）～（15），Jy=u为不确定变量的约束；c、D、A、F、G、J为对应约束的系数矩阵；d、h为对应约束的常数列向量.

式（22）中的三层模型对应了一个两阶段问题，其中，对应的第一阶段决定了储能、电动汽车及系统购售电的运行状态，该阶段需保证系统能够应对不确定集中任意场景，在一阶段决策的状态下，第二阶段则需求出各单元的输出变量，并求解出最恶劣的运行场景.

3 模型求解

目前，解决两阶段模型问题的算法主要有Benders分解算法[18]和 C&CG 算法.与 Benders分解算法相比，C&CG算法的迭代次数更少，收敛速度更快[19].故本文采用C&CG算法进行模型求解.C&CG算法将“min-max-min”问题分为主问题和子问题进行求解.

1）主问题

主问题为外层的“min”问题，用于求解最小成本.假设主问题能在l次迭代后求得最优解，在得到子问题第k次的最优解（xk，uk）后，将子问题的解带入主问题，主问题的形式为

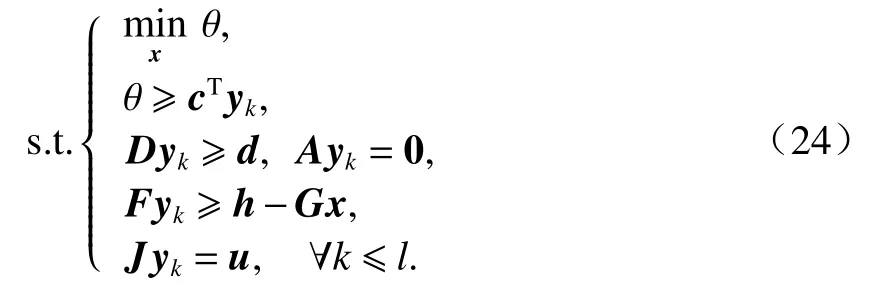
2）子问题

子问题为内层“max-min”问题，用于求解最恶劣场景.根据强对偶理论，引入对偶变量将其转化为max问题，转化后如式(25)、(26)所示.

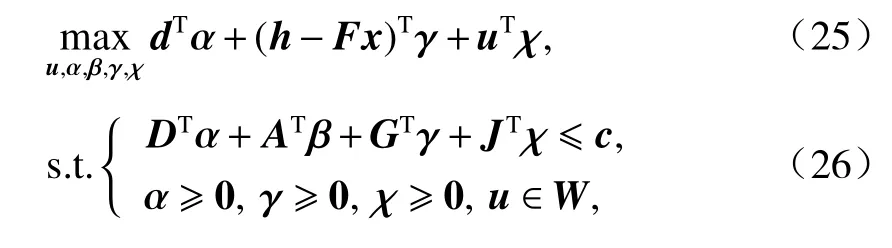
式中：α、β、γ、χ分别为式（22b）中系数矩阵对应的对偶变量，uTχ为双线性项，转化后的max问题为NP-hard问题.

针对本文研究对象而言，极端场景即为风光微源出力在各调度周期各时段皆处于预测区间最小值，交直流负荷则在各调度时段皆处于预测区间最大值.结合文献[20]结论可知：极端场景是不确定集W的极点，即不确定集的边界，故当Γj取为整数时，对应的或取为1，转化成了二进制变量.故采用BIG-M法[21]，通过引入连续辅助变量和相关约束，经过推导和转换，将子问题转换为混合整数线性规划问题进行求解.

分解后采用C&CG算法求解，流程如图2所示.

图2 C&CG 算法流程Fig.2 Flowchart of column and constraint generation algorithm

4 算例分析

本文选取某地交直流微电网夏季典型日的风速、光照以及交直流负荷数据为例进行仿真，分析了EVs的运行方式对微电网经济运行的影响，得出了在鲁棒最优成本下最优接入辆数，在电动汽车接入最优情况下分析了调度方案的经济性和有效性.

考虑风机、光伏以及交直流负荷的波动性，分别取最大波动为预测值的20%、15%以及10%[22]，仿真相关基本参数如表1所示，光伏、风机的预测出力及交直流负荷功率如图3、4所示.表1中：EEvi,o为第i辆车的初始容量.微电网日前交易电价以配电网分时电价作为参考，如表2所示.电动汽车动力电池参数见文献[13].由于电动汽车的频繁充放电对动力电池寿命有较大影响，结合用户出行规律、负荷的峰谷期及电价水平，考虑电动汽车的接入时间为00：00—07：00 以及 17：00—24：00.

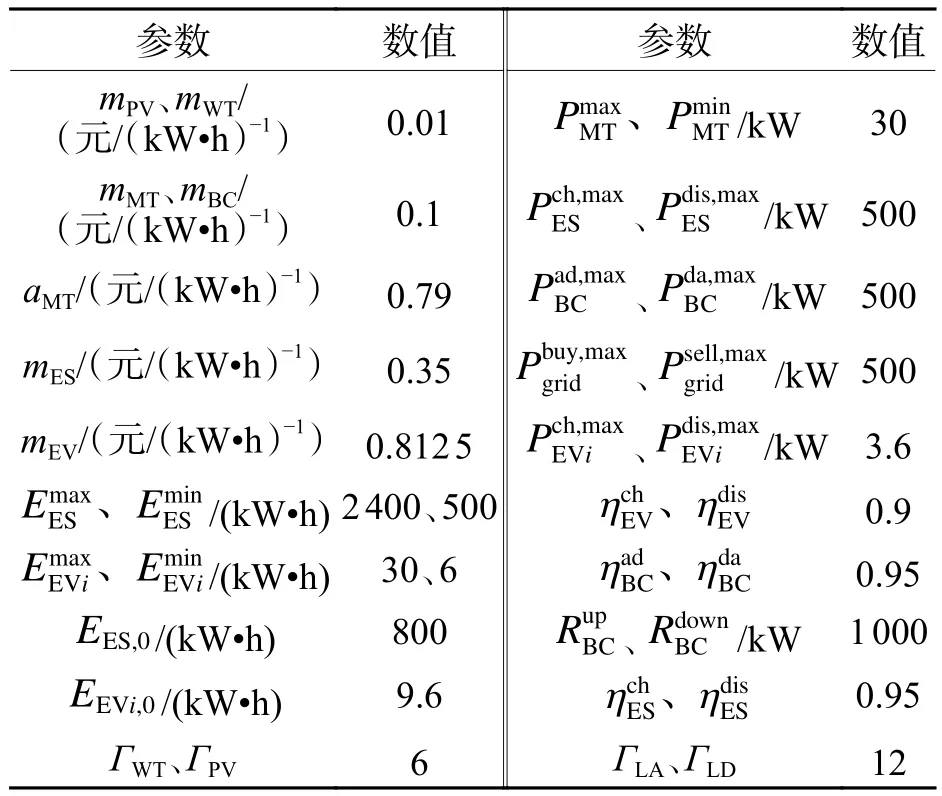
表1 基本参数设置Tab.1 Basic parameter setting

表2 配电网分时电价Tab.2 Time-of-use prices for distribution network

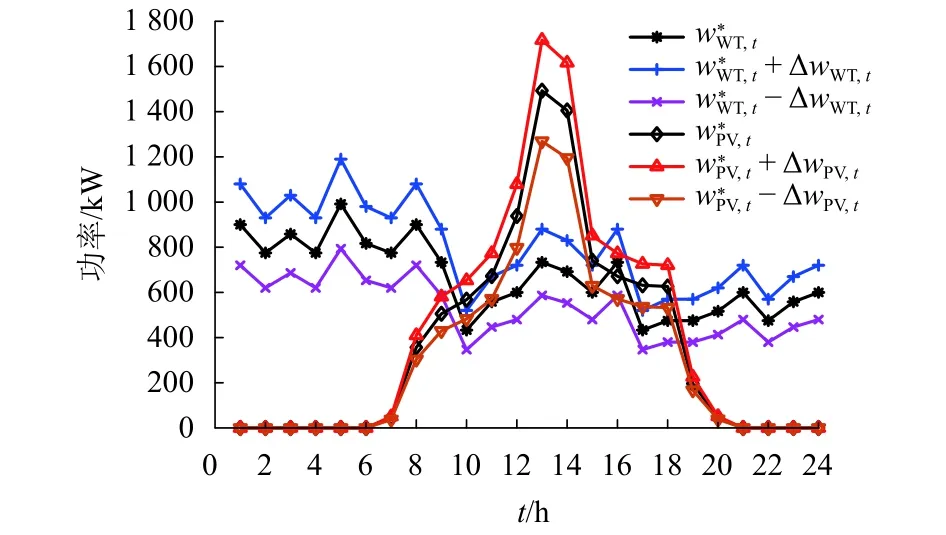
图3 风机、光伏出力不确定集Fig.3 Uncertainty set of wind turbine and photovoltaic output

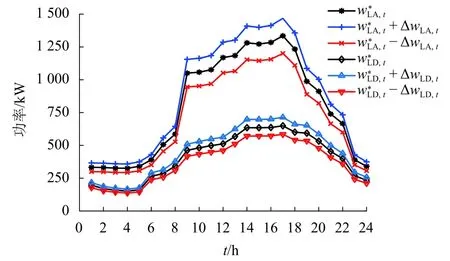
图4 交流负荷及直流负荷不确定集Fig.4 Uncertainty set of AC load and DC load

4.1 EVs接入对微电网的影响分析

1）EVs随机充电模式对微网经济运行的影响

电动汽车随机充电负荷可根据文献[23]中的用户出行模型模拟得出.考虑50辆EVs接入微网运行的情况，采用蒙特卡洛算法进行模拟，得到电动汽车出行负荷如图5所示.

图5 电动汽车随机充电负荷（50 辆）Fig.5 Random charging load of 50 electric vehicles

将充电负荷代入模型中进行仿真计算调度方案运行成本，并将运行成本与集中调度模式下有序充放电调度方案的运行成本对比，结果见表3.

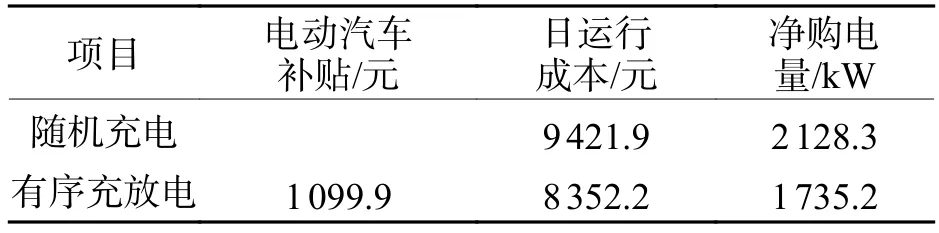
表3 电动汽车随机充电与有序充放电仿真结果对比Tab.3 Simulation results of randomly charging and orderly charging and discharging for electric vehicles

从表3可以看出：在随机充电模式下，系统虽节省了对电动汽车用户的补贴成本，但其日运行成本较有序充放电模式下的成本高出1 069.7元，向配电网的净购电量也有所增加.这是由于在随机充电模式下，电动汽车仅充当了负荷的角色，且该负荷主要集中在系统的用电高峰时期，造成了总体负荷的“峰上加峰”，增加了微电网在电价高峰时期的购电量，进而增加了系统的运行成本.综上，合理运用EVs的源荷特性，能够有效降低微电网的日运行成本，提高系统运行经济性.

2）EVs有序充电模式对微网经济运行的影响

不同EVs辆数下的微电网日前调度成本曲线如图6所示.

图6 不同电动汽车辆数下的调度运行成本Fig.6 Operation costs for different numbers of electric vehicles

从图6可以看到：随着参与调度的EVs辆数的增加，调度费用呈现出先下降后上升的趋势.其原因在于随着EVs的增加，其存储电量也随之增加，在一定数目下，EVs可与储能单元一同放电实现负荷的削峰填谷，减少微电网在电价峰值时的购电费用，降低运行成本，但EVs增加的同时，也减少了储能在电价低谷时段的充电电量.电价低谷时段，直流区域的电能主要来自交流区域的换流功率，当接入的电动汽车过多时，换流功率将满足不了直流负荷与EVs充电负荷的需求，此时只能通过储能放电给EVs充电，这就造成了调度费用的叠加，从而导致运行成本增加.故当换流功率恰好能满足EVs所需功率及直流负荷功率时，系统运行成本取最小值.EVs最优接入辆数Ibest可通过式（27）得，所得最优接入辆数为74辆.

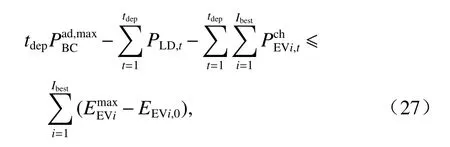
式中：tdep为电动汽车离家时间.

4.2 模型分析

1）优化结果分析

综上EVs接入对微网的影响分析可知，合理安排电动汽车的有序充放电能够有效减少系统运行成本，提高微电网运行的经济性与供电可靠性.故本文取鲁棒最低成本下的接入辆数（74辆）为例，分析本文搭建的模型的科学性和有效性.优化结果如图7所示.

图7中：在 00：00—07：00电价低谷时段，燃气轮机的调度费用高于电价，故其一直以最小出力运行；除去08：00—09：00时段由于最大售电功率的限制，其余时段为应对峰平时段的负荷高峰，微型燃气轮机一直以最大功率运行，由于夜间无光照，微电网主要通过风机出力及向配网购电维持运营，换流器以最大换流功率从交流区域输送电能至直流区域，以保证直流负荷正常运行以及储能单元和EVs的充电；8：00—14：00时段，光伏出力逐渐增大，在满足直流区域的负荷供给下，直流区域的电能通过换流器流入交流区域，以保证系统运行，并在电能富余时向电网售电；在12：00—15：00时段，由于换流功率限制，直流侧多余的电能由储能吸收，7：00—17：00为EVs出行时段，不参与系统调度；在17：00后电动汽车用户回到家中，由于负荷晚高峰的到来，EVs及储能协同放电以减少系统向配网的购电量，实现负荷的削峰填谷，降低系统运行费用.

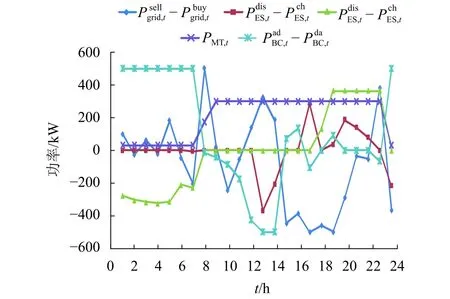
图7 优化结果Fig.7 Optimization results

2）经济性分析

微电网调度分为日前调度和实时调度两个阶段.日前调度阶段，微电网需根据优化结果制定调度计划上报给配网以供配网参考.实时调度阶段中，微电网需根据出力与负荷的实时功率进行调整，保证系统可靠运行.当微电网出力减小或是负荷功率增大时，系统就需要向实时电力市场购电以保证供需平衡，因此在实时调度过程中会产生日前调度计划外的额外费用，即补偿成本.由于实时市场的价格一般要高于日前电价，考虑实时电力市场电价为日前电价的两倍[24]，在本文所考虑的不确定区间范围内生成实际运行数据，为分析模型的经济性，选取4种不确定预算情况，计算模型在不同不确定预算下的日前调度成本及实时运行时的补偿成本，结果如图8所示.

由图8可知：随着不确定预算的增加，模型保守性增大，日前调度成本也不断增大，与此同时，系统的鲁棒性也随之提升，在实时调度阶段，实时调整成本随着不确定预算的增大而减小，最终所得的综合运行成本也随之减小，说明了本文搭建模型的经济性.

图8 不同不确定预算下微电网综合运行成本Fig.8 Integrated operation cost of microgrid under different uncertain budgets

值得注意的是：当不确定预算均为0时，模型为确定性优化，对比鲁棒优化，确定性优化的日前调度成本是最小的，但结合实时调整成本后，综合成本确是最大，这就意味着，微网在确定性优化所得方案下运行会为系统带来较大的风险，反映了微电网优化运行中考虑不确定性的重要性.

5 结 论

本文结合电动汽车的源荷特性，考虑交直流微网中的微源出力与负荷功率的不确定性，搭建了基于两阶段鲁棒调度的含电动汽车的交直流微电网的运行优化模型，采用C&CG算法进行求解.分析结果表明：

1）与EVs无序充电接入微网相比，EVs的充放电模式能够有效降低系统向配网的购电量，降低系统运行成本.

2）由于换流器功率限制，当接入EVs超过一定数量时，换流功率不再能满足EVs充电负荷需求，此时会造成调度费用的叠加，运行成本反而增加.故适当增加换流器配置能够有效接纳EVs，提高系统运行的经济性.

3）在日前调度阶段，与确定性调度相比，鲁棒调度的成本较高，但结合次日实时调度中所产生的调整成本，鲁棒调度的综合成本较确定性调度低，说明了鲁棒模型可抵御实时运行中的价格波动风险，降低系统的实时调整成本，从而降低综合运行成本.

4）不确定预算能够灵活调节模型的保守性，不确定预算增大，模型的鲁棒性能也随之增强.在实际运营中，调度人员可通过调节不确定预算大小在系统鲁棒性及经济性之间进行合理选择.