CRTS Ⅱ型轨道板的高频振动疲劳特性分析

陈 醉 ，刘学毅 ，胡 颖 ，曹瑞恒 ，肖杰灵 ，杨荣山

（1.西南交通大学高速铁路线路工程教育部重点实验室，四川 成都 610031；2.西南交通大学土木工程学院，四川成都 610031）

CRTS Ⅱ型板式无砟轨道（以下简称“Ⅱ型板”）是我国高速铁路的主型轨道结构之一，无砟道床主要由轨道板、宽窄接缝、CA砂浆层、支承层等组成，轨道板通过纵向连接器及混凝土组成的结构实现连接，形成纵连式轨道[1].根据运营线路的现场调研，Ⅱ型板总体使用情况良好，但随着高速铁路运营时间的推移，受大规模施工作业、多变的下部基础和经时效应下的结构退化等因素限制，轨道结构不可避免地会产生局部伤损[2].无砟轨道结构的疲劳耐久性是保证其设计寿命的主要指标，根据当前高速铁路无砟轨道的设计理论与方法，采用混凝土设计规范对其疲劳特性和耐久性进行检算时，既有无砟轨道均满足要求[3].但无砟轨道在实际运营过程中出现了多种形式的疲劳损伤，尤其是在轨道的新老混凝土结合面，该现象更为普遍，如轨道板与砂浆层的层间脱连.轨道板在列车轮载作用下呈上压下拉的受弯形态，因混凝土受拉压特性的差异性，轨道板的损伤多表现为由板底发展的裂缝[4].列车轮载的高频疲劳作用也会使结构内部损伤不断累积，导致刚度下降、变形增加，最终引发结构的损坏.

目前针对混凝土的疲劳损伤普遍采用Miner线性准则与S-N曲线作为评估方法，如宋玉普等[5-7]通过对混凝土多轴疲劳试验的分析，建立多种应力状态下混凝土疲劳的S-N曲线和疲劳破坏准则；Cornelissen等[8]通过修正混凝土的S-N曲线，论证了压应力对混凝土的抗拉疲劳破坏有负面影响；Dobromil等[9]通过将S-N曲线转化为材料损伤的方法，提出了一种适用于高周疲劳的混凝土裂缝损伤新模型.传统的疲劳损伤判定法则仅考虑荷载幅值与次数的作用，未考虑荷载频率对损伤的影响.列车轮载作用下无砟轨道混凝土结构应力幅值一般较低，但是荷载的循环次数很高，属于复杂应力状态下的高周疲劳问题[10]，因此针对无砟轨道使用寿命预测方法应区别于普通混凝土结构的寿命预测.

针对无砟轨道的疲劳损伤问题，徐庆元等[11-12]对荷载组合作用下桥上纵连板式无砟轨道疲劳应力谱、疲劳寿命分析模型及疲劳破坏关键技术参数进行了研究；Poveda等[13]与Tarifa等[14]分别通过数值仿真与现场试验的方法，研究了框架式无砟轨道在列车时变荷载作用下的瞬态效应，通过分析应力幅值的影响，提出了针对框架式无砟轨道的疲劳准则；Konings[15]基于Miner线性疲劳损伤准则和钢筋混凝土S-N曲线，初步分析了服役期间复杂载荷下RHEDA 2000型无砟轨道的疲劳寿命；刘学毅等[16]通过对先张与后张Ⅲ型轨道板的疲劳试验，研究了轨道结构各部件位移及轨道板应力随环境温度及列车轮载疲劳作用次数的变化；童明娜等[17]针对Ⅱ型板潜在的疲劳失效模式，建立列车荷载与温度荷载共同作用下轨道板混凝土疲劳功能函数，开展了基于时变可靠度理论的疲劳时变可靠性研究.Chapeleau等[18]开展了无砟轨道实尺模型试验，通过测量轨道板内疲劳应变，探索了板中裂纹的扩展规律.

上述研究主要通过数值仿真与现场试验的方法，关注了无砟轨道结构整体的疲劳特性，并初步探索了损伤发展机理，但针对列车高频轮载作用下无砟轨道疲劳特性的研究尚需深入.特别是在轮对作用间隙阶段，列车高频轮载会引发板体的自振效应，轨道结构会产生微小的高频振动，针对该阶段振动对轨道结构疲劳特性的影响，目前鲜有系统的研究.故深入探讨列车高频荷载下轨道板的疲劳特性以及轨道板自振效应对疲劳寿命的影响程度，对预防无砟轨道进入故障高发期、保证列车的安全高效运行具有重大的现实意义.

1 计算模型与参数

建立如图1所示的分析模型研究局部脱空下轨道板的疲劳特性，相应的有限元模型局部如图2所示，并作如下基本假定：

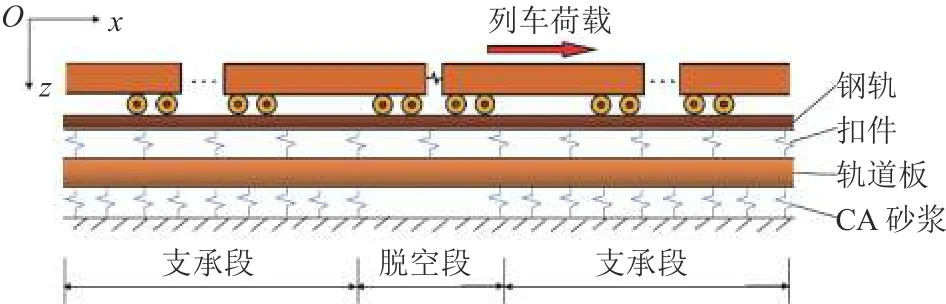
图1 轨道结构垂向振动分析模型Fig.1 Vertical vibration analysis model of track structure

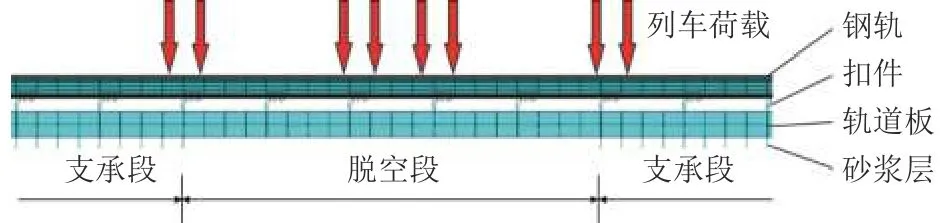
图2 有限元模型局部示意Fig.2 Local schematic diagram of finite element model

1）钢轨、轨道板简化为均质的连续弹性支承欧拉梁；

2）扣件简化为线弹性点支承；砂浆层简化为均布的弹性支承，忽略轨道板脱空处砂浆层的支承作用；

3）忽略支承层及其他轨道附属结构对轨道板振动的影响.

图2有限元模型采用欧拉梁单元模拟轨道板、钢轨，为消除边界效应建立共计16块板长（约100 m），并选取模型中部轨道板作为分析对象；扣件采用线弹性的离散弹簧单元模拟；轨道板支承段与底座板之间的砂浆层约束简化为均布的线弹性约束.列车轮载模式是计算疲劳效应的基础，以移动恒载模拟列车轮载作用，并通过瞬态分析方法获取轨道板的受力形态.以京沪高速铁路为研究背景，按照京沪线上的主要车型CRH380建立典型车辆模型[19]，模拟两个车辆，共计4个转向架、8个轮对以360 km/h的速度顺序通过钢轨，其中列车轴重为170 kN.模型主要参数如表1所示[1,2].

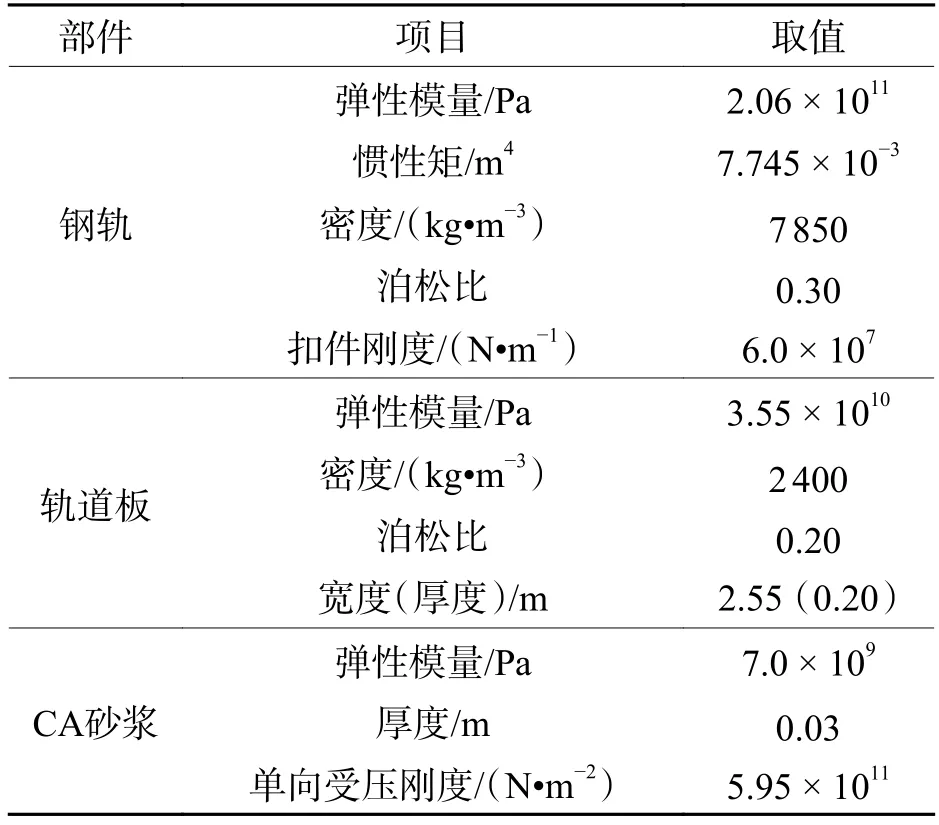
表1 主要计算参数Tab.1 Main calculation parameters

2 轨道板振动力学特性分析

2.1 振动受力分析

受温度、水及列车动荷载等多场耦合荷载共同影响，砂浆层与轨道板间的粘结状态在线路运营后将极大减弱，板底部属于受力的薄弱部位，因此有必要关注轨道板在列车移动荷载作用下板底的受力形态.为探究轨道板在列车移动荷载作用下的受力特性，假定脱空长度为L0，轨枕间距为La，以L0= 0，2.0La，5.0La为例，分析轨道板在列车移动荷载作用下的弯矩时程分布规律，结果如图3所示.

图3表明，轨道板弯矩在轮对行驶于分析点正上方时达到最大值.L0= 0 时，轨道板承受弯矩较小，弯矩量值为 0.505 kN·m，此时板底拉应力为0.03 MPa，远小于Ⅱ型板C55混凝土的抗拉强度2.74 MPa，因此在轨道结构完好的条件下，列车轮载引发轨道板伤损的可能性较小.L0= 2.0La，5.0La时，弯矩量值分别为9.66、32.2 kN·m，根据受弯梁的正应力计算方法可得板底拉应力分别为0.56、1.89 MPa，初步计算表明，当L0= 6.2La时，轨道板在单次轮对荷载作用下即达到轨道板的抗拉强度极限.

根据列车移动荷载分布特性，轨道板振动弯矩大致可分为5个阶段（见图3）：列车行驶于分析点前的阶段（阶段O）、第1车辆前转向架作用阶段（阶段Ⅰ）、同一车辆的前后2个转向架作用间隙阶段（阶段Ⅱ）、相邻车辆的2个转向架共同作用阶段（阶段Ⅲ）、列车行驶于分析点后的阶段（阶段A）.图3表明，不同时间点相同阶段的振动弯矩时程分布基本相同（如图3中2个阶段Ⅰ与2个阶段Ⅱ），阶段O、Ⅱ、A的弯矩时程变化规律相近，阶段Ⅲ大致相当于2个阶段Ⅰ的作用效果.以16车编组的CRH380列车为例，当1列车经过分析点时，轨道板弯矩时程曲线将经历共计1组阶段O、2组阶段Ⅰ、16组阶段Ⅱ、15组阶段Ⅲ、1组阶段A.此外，在列车行驶于分析点前后（阶段O、A）以及2个转向架之间的阶段（阶段Ⅱ），因列车轮载引发了板体的自振效应，轨道板仍有量级较小的弯矩，但此时的弯矩变化频率远大于轮对行驶于分析点正上方时的弯矩变化频率，故在轨道结构疲劳分析过程中不应该予以忽略.

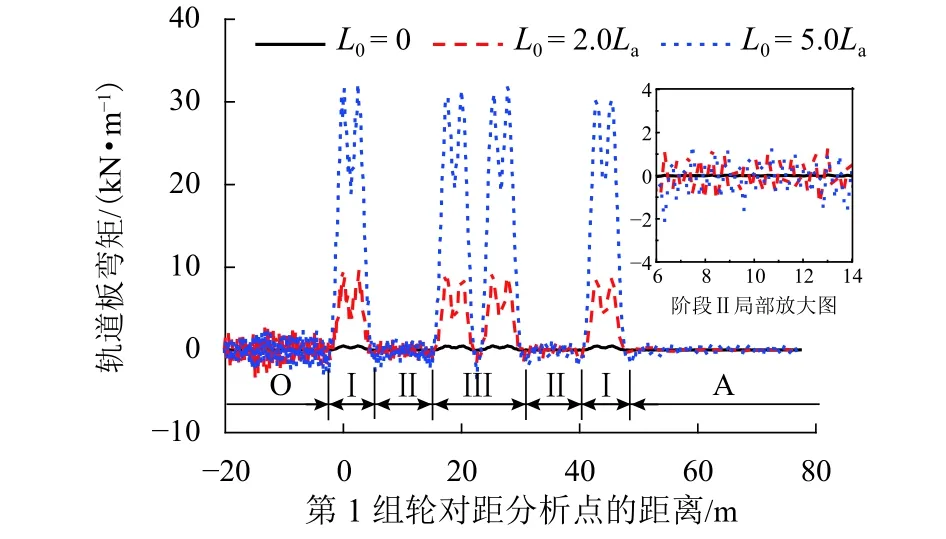
图3 轨道板弯矩时程分布规律Fig.3 Time history distribution of track slab bending moments

2.2 自振频率分析

列车轮载为典型的周期性荷载，当荷载作用频率与轨道板自振频率相近时，易引发轨道结构的共振，此时列车轮载引发板体的自振效应可能会加剧轨道结构的疲劳损伤.为探究轨道板振动频率分布特性，以L0= 0～10.0La为例，分析L0对轨道板自振频率的影响，结果如图4所示.

图4 局部脱空影响下轨道板自振频率Fig.4 Natural frequencies of track slab under the effect of partial de-bonding

图4表明，轨道板自振频率与脱空长度呈负增长关系.当轨道板不发生脱空时，轨道板的振动主要受砂浆层支承刚度的约束影响[20]，因此轨道结构各阶自振频率集中于 3 500 Hz 的量值.当L0＜ 3.0La时，轨道板的高阶频率相近，其量值亦集中于3 500 Hz，表明此时高阶频率引发的是轨道板支承段的局部振动.当L0＞4.0La后，轨道板的自振频率随阶数增长，表明此时轨道板的振动能量主要集中于脱空段.

目前针对无砟轨道结构振动特性的分析普遍采用高速列车的车轮通过频率作为加载频率，假定列车轮载以恒定速度通过，若某一轴距对应的加载频率与自振频率相近，有引发轨道板共振的风险.定义该轴距为临界轴距，若行车速度为360 km/h，局部脱空影响下列车轮载引发轨道结构共振的临界轴距如图5所示.

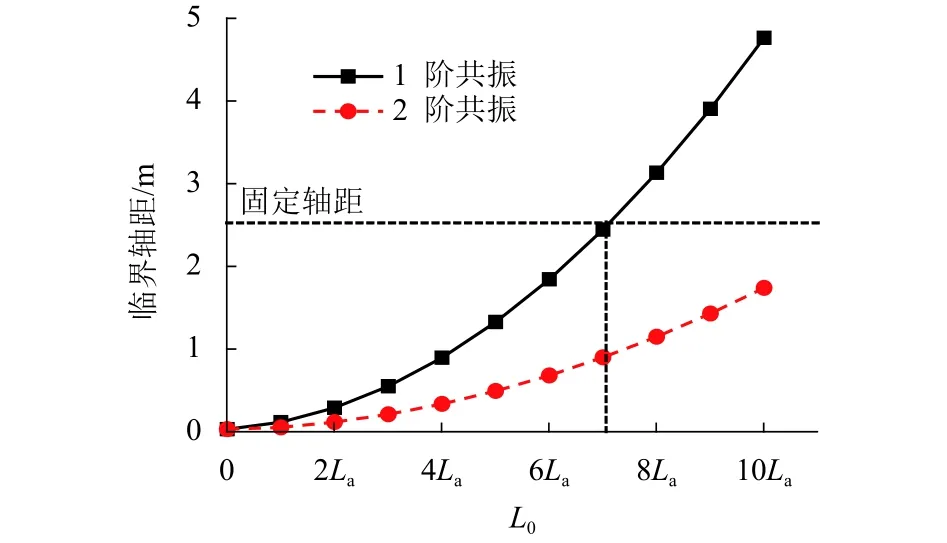
图5 引发轨道结构共振的临界轴距Fig.5 Critical wheelbase for resonance of track structure

图5表明，引发轨道结构共振的临界轴距与脱空长度成正增长关系.CRH380车型的典型轴距主要有：固定轴距为2.5 m，同一车辆的前后两个转向架中心距为17.375 m，相邻车辆的两个转向架中心距为 7.650 m，车辆间距为 25.025 m[20].图5 表明，若行车速度为360 km/h，仅固定轴距有引发轨道板共振的风险.若L0=0，此时的临界轴距约为 0，故可认定轨道结构完好时，列车轮载不会引发轨道板的共振；L0小于整块板长时，列车轮载不会引发轨道板的高阶共振;L0=7.0La时，临界轴距与单组转向架的轴间距相等，表明此时列车轮载有引发轨道板1阶共振的风险，综合前述分析结果，列车轮载在引发轨道板共振前即发生板底开裂.

3 轨道板振动疲劳特性分析

3.1 疲劳寿命预测方法

在建立轨道板寿命预测模型时，采用工程上常用的Miner线性损伤累积理论进行计算[21]，当各种受载情况的损伤之和等于1时，轨道板发生疲劳破坏，即

式中：ni为第i阶段时疲劳荷载的当前作用组数，i=O,Ⅰ,Ⅱ,Ⅲ,A；Ni为第i阶段时应力水平的疲劳作用总组数.

由于轨道板混凝土抗拉强度远小于抗压强度，故在疲劳特性分析过程中只考虑拉应力部分的计数.Tepfers等[21]通过拉伸疲劳试验推导出了混凝土单对数疲劳方程, 以列车组数作用下的疲劳破坏荷载循环次数为例，疲劳寿命方程表示为

式中：R= σmin/σmax为应力比， σmax、 σmin分别为疲劳应力的上、下限；S=σmax/ft为应力水平，ft为混凝土抗拉强度；a、b为疲劳试验所确定的系数，a=1.0，b=0.061 101 12[22]；NS为疲劳破坏时作用的列车组数.

当列车作用组数为1时，轨道板将承受共计64组轮对冲击（2组阶段Ⅰ、15组阶段Ⅲ）、17组高频自振（1组阶段O、1组阶段A、15组阶段Ⅱ）的作用，因此，NS与NO、NI、NⅡ、NⅢ、NA的关系为

式中：αi为第i阶段的荷载周期系数，根据16车编组 CRH380 列车的特点，取αO= 1，αI= 2，αⅡ= 16，αⅢ=15，αA= 1.

文献[22]表明，式(2)在应力比较高时计算结果虽偏大，但满足实际工程的使用要求.因此，可基于式(1) ～ (3)分析Ⅱ型板的高频振动疲劳特性.

通过有限元法得到列车移动荷载作用下轨道板分析点的弯矩时程曲线，换算成板底应力后采用雨流计数法[23]对应力时程曲线进行各阶段的计数，由此得到相应的轨道板疲劳应力谱，代入式(1)～(3)确定轨道板的疲劳寿命.

各阶段对疲劳寿命的影响系数为

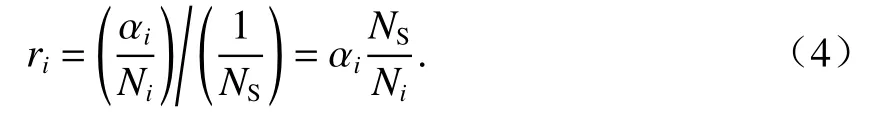
若以阶段Ⅰ、Ⅲ的弯矩时程分布为例，分析列车轮载作用下无脱空轨道板的疲劳寿命，此时同一转向架上2个轮载存在叠加效应，轨道板在上述2个阶段出现幅值约为0.03 MPa的最大拉应力，通过雨流计数法得到该阶段列车轮载对轨道板体产生了幅值 0.012 MPa、均值 0.018 MPa 的疲劳应力，共计64组.式(1)～(3)计算表明，仅考虑荷载作用次数时（即仅考虑阶段Ⅰ、Ⅲ的疲劳荷载计数），当2.98 ×1013个列车组作用后，轨道板即发生疲劳破坏；若另考虑阶段O、Ⅱ、A板体自振的影响，以相同的计数方法算得考虑列车轮载引发板体自振的效应后，疲劳寿命为1.66 × 1013个列车组，表明考虑板体自振后，列车轮载对轨道板产生了约1.8倍的疲劳荷载当量.

3.2 脱空长度对疲劳特性影响

3.1节分析表明，阶段Ⅱ、Ⅲ具有较强的周期性，故以这2个阶段为代表，分别分析轨道板自振、列车轮载对结构疲劳特性的影响.轨道板在L0= 0～6.0La的条件下，阶段Ⅱ、Ⅲ疲劳寿命值、疲劳寿命影响系数及疲劳寿命总值如图6所示.

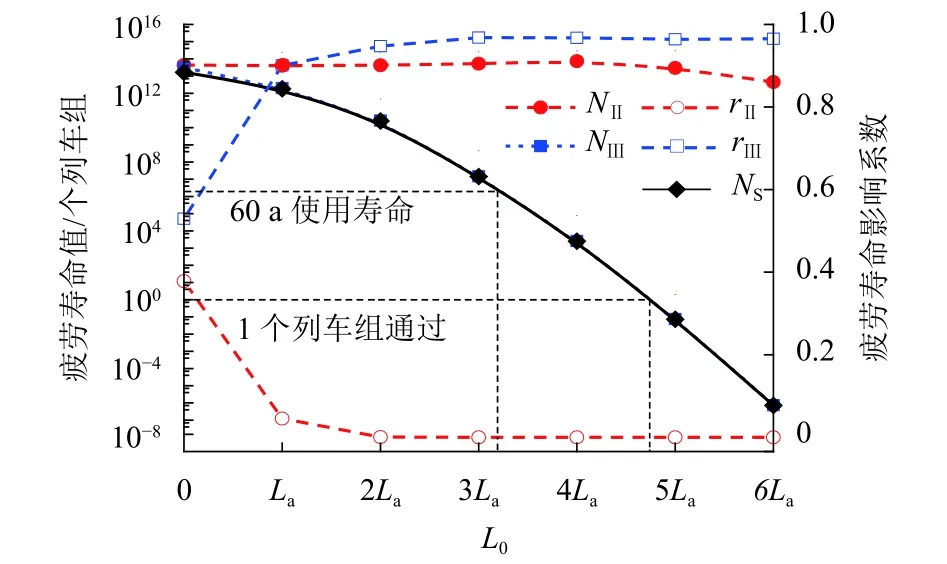
图6 不同脱空长度下轨道板疲劳寿命值Fig.6 Fatigue lifes of track slab with different de-bonding lengths

图6表明，L0越长，轨道板越容易发生疲劳损伤.当L0＞4.7La后，轨道板在 1 个列车组的作用下即发生疲劳破坏.一般认为，无砟轨道的使用寿命是60 a，假定运营时每天作用100个列车组[19]，则60 a 内将有 2.19 × 106个列车组通过，对应于图6的L0= 3.2La.阶段Ⅱ的疲劳寿命受轨道板脱空长度影响较小，疲劳寿命大约维持在4.10 × 1013个作用组，当L0= 0时，阶段Ⅱ的疲劳损伤影响系数为0.378；当板底发生脱空后，随着板体自振频率降低，阶段Ⅱ的疲劳应力作用次数减小，故该阶段对疲劳寿命的影响程度减弱，此时阶段Ⅲ对应的疲劳作用总组数逐渐接近于疲劳寿命总值.L0=La时，阶段Ⅱ、Ⅲ的疲劳损伤影响系数分别为0.046、0.901；当L0＞2.0La后，阶段Ⅱ的疲劳寿命影响系数趋于0，表明此时可按传统的仅考虑列车轮载作用次数的计数方法进行疲劳寿命预测.因此，轨道板L0＞3.2La后，现场无砟轨道难以维持60 a的使用寿命；当L0＞2.0La后，可忽略列车轮载引发板体自振的效应对疲劳损伤的影响.

4 结 论

1）轨道结构完好时，列车轮载引发轨道板伤损的可能性较小.若列车行车速度为 360 km/h，L0=6.2La时，轨道板在单次轮对荷载作用下即达到轨道板的抗拉强度极限；L0=7.0La时，列车轮载有引发轨道板共振的风险，表明列车轮载在引发轨道板共振前即发生板底开裂.

2）当L0＞4.7La后，轨道板在 1 个列车组的作用下即发生疲劳破坏；L0＞3.2La后，现场无砟轨道难以维持60 a的使用寿命.

3）轨道结构完好时，列车轮载引发的板体自振效应对轨道板疲劳损伤影响程度最大，此时在考虑板体自振后，列车轮载对轨道板产生约1.8倍的疲劳荷载当量；当L0＞2.0La后，可忽略板体自振对疲劳损伤的影响.