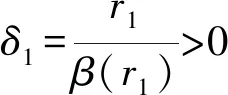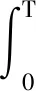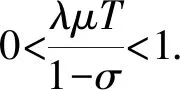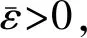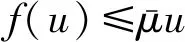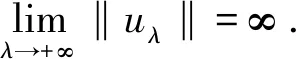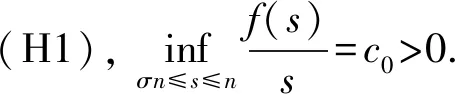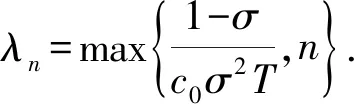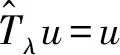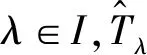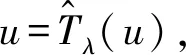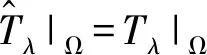一类一阶周期边值问题多个正解的存在性

吴梦丽

(西安电子科技大学数学与统计学院, 西安 710126)

1 引 言

一阶周期边值问题在生物学,经济学,生态学等领域有着广泛应用.近年来,对一阶含参方程周期正解存在性的研究出现了一些进展[1-8]，如Ma等[3]应用锥上不动点定理研究了f在0处和∞处满足不同的条件及g在有界的条件下方程

u′(t)=a(t)g(u(t))u(t)-λb(t)f(u(t-τ(t))

(1)

周期正解存在性.其中，文献[2]通过定义正算子和锥得到了下面的结果：

定理A假设

(A1)λ>0是一个参数;

(A3)f,g∈C([0,∞),[0,∞))且当s>0时,f(s)>0,τ(t)是ω-周期函数.

若f0=f∞=0,则存在0<μ*<μ*，当μ>μ*时问题(1)存在两个周期正解;当0<μ<μ*时,问题(1)不存在周期正解.

值得注意的是，在定理A中当μ∈[μ*，μ*]时，问题(1)周期正解的存在性未知，μ*能否和μ*相等也是问题.受上述文献的启发,本文在f单增的条件下运用上下解方法及 Leray-Schauder 度理论考虑如下一阶周期边值问题

多个正解的存在性.

本文总假定

本文主要结果如下：

定理1.1设(H1)成立.则当λ充分小时,问题(1)不存在正解,当λ充分大时,问题(2)存在两个正解.

定理1.2设(H1)成立.则存在λ*>0,使得当0<λ<λ*时问题(2)不存在正解;当λ=λ*时问题(2)至少存在一个正解;当λ>λ*时问题(2)至少存在两个正解.

2 预备知识

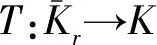
(i) 若x∈∂Kr满足‖x‖≤‖Tx‖,则

i(T,Kr,K)=0.

(ii) 若x∈∂Kr满足‖x‖≥‖Tx‖,则

i(T,Kr,K)=1.

本文的工作空间是

X={u(t):u(t)∈C[0,T],u(0)=u(T)},

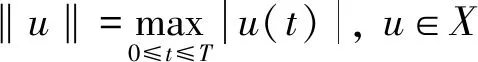
K={u∈X:u≥0,u(t)≥σ‖u‖,t∈[0,T]},

C={u∈X:u>0,t∈[0,T]}.

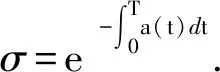
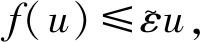
Ωr={u∈K:‖u‖

其中r为正参数,∂Ωr={u∈K:‖u‖=r}.定义算子Tλ:X→X为

其中

当0≤s≤T时满足

引理2.2对问题(2)中的f(u)有Tλ(C)⊂K且Tλ:K→K是全连续算子.

证明 对任意的u∈C,t∈[0,T],有

σ‖Tλu‖.

因而Tλ(C)⊂K.由Arzela-Ascoli定理[10],易证Tλ:K→K是全连续算子.证毕.

3 上下解

定义3.1[11]如果x∈X∩C1[0,T]且满足

x′(t)+λf(x(t))-a(t)x(t)≤0, 0

则称x是问题(2)的上解.

定义3.2[11]如果y∈X∩C1[0,T]且满足

y′(t)+λf(y(t))-a(t)y(t)≥0, 0

则称y是问题(2)的下解.

引理3.3设(H1)成立.若x(t)和y(t)分别是问题(2)的上解和下解，且满足当t∈[0,T]时y(t)≤x(t),则至少存在一个解u(t)且满足y(t)≤u(t)≤x(t).

证明 首先考察辅助问题

其中

f*(u(t))=f(Px,y(u(t)))-

arctan[u(t)-Px,y(u(t))]

(4)

Px,y(u(t))=max{y(t),min{u(t),x(t)}}

(5)

则

(6)

显然,如果辅助问题(3)的解u满足当t∈[0,T]时y(t)≤u(t)≤x(t),那么由式(3)至式(5)和问题(2)知问题(3)的解也为问题(2)的解.故只需要证明问题(3)的解u满足y(t)≤u(t)≤x(t).

下面我们先证明当t∈[0,T]时u(t)≤x(t).令ω(t)=u(t)-x(t).反设存在一个t*∈[0,T]使得ω(t*)>0.我们分下面三种情形讨论.

情形1t*∈(0,T)使得ω(t*)=u(t*)-x(t*)>0.不失一般性,设ω在t=t*处取得最大值.则u′(t*)=x′(t*).另一方面,由定义3.1和(3)至(6)式可得

u′(t*)=a(t*)u(t*)-λf*(u(t*))=

a(t*)u(t*)-λf(Px,y(u(t)))+

λarctan[u(t*)-Px,y(u(t*))]≥

a(t*)u(t*)-λf(x(t*))+

λarctan[u(t*)-x(t*)]≥

a(t*)x(t*)-λf(x(t*))+

λarctan[u(t*)-x(t*)]≥

x′(t*)+λarctan[u(t*)-

x(t*)]>x′(t*).

这与u′(t*)=x′(t*)矛盾.

情形2t*=0.则ω(0)>0且在t∈(0,T]上ω(t)≤0.另一方面,由定义3.1可知ω(0)=u(0)-x(0)=u(T)-x(T)=ω(T)≤0.这与ω(0)>0矛盾.

情形3t*=T.则ω(T)>0且在t∈[0,T)上ω(t)≤0.另一方面,由定义3.1可知ω(T)=u(T)-x(T)=u(0)-x(0)=ω(0)≤0.这与ω(T)>0矛盾.故当t∈[0,T]时u(t)≤x(t).同法可证得当t∈[0,T]时u(t)≥y(t).引理得证.

4 主要结果的证明

定理1.1的证明 若q>0,则

Kr1={u∈K:‖u‖≤r1}.

当λ>δ1,u∈∂Kr1时,有

δ1β(r1)=r1=‖u‖,

Kr3={u∈K:‖u‖

如果u∈∂Kr3,则u(t)≥σ‖u‖≥H.从而

即‖Tλu‖<‖u‖.由引理2.1得i(Tλ,Kr3,K)=1.由不动点指数的可加性得

r2<‖u1‖

u1,u2就是问题(2)的两个正解.

即

矛盾.定理得证.

下面我们将运用上下解和拓扑度的方法来证明定理1.2.为保证问题(2)的所有可能解都是非负的,我们对f做延拓使得

f(s)=f(0),s<0

(7)

首先证明下面的引理.

引理4.1假设(H1)成立.令I⊂(0,∞)是紧子集.若λ∈I,则存在一个常数bI>0使得问题(2)的所有解均满足‖u‖≤bI.

选取n充分大使得σ‖un‖≥q1.则有

矛盾.引理得证.

现在令Γ表示问题(2)正解存在的λ>0的集合.由定理1.1,Γ非空且有界.设λ*=infΓ.从而有0<λ*<∞.下证λ*∈Γ.

首先，令λn→λ*,其中λn∈Γ,

λ1>λ2>…>λn-1>λn>…>λ*.

因为{λn}有界,由引理4.1,对应问题(2)的解{un}有界.由积分算子Tλ的紧性易得λ*∈Γ.因此,当λ=λ*时,问题(2)至少有一个解存在.令u*为问题(2)对应λ=λ*的解.

设u*为问题(2)的解,对应的λ取λ*.定义

令

考虑

Ω={u∈X:-ε≤u(t)≤u*(t)+ε}.

-(u*(t)+ε)′+a(t)(u*(t)+ε)=

且

(u*+ε)(0)=(u*+ε)(T).

由定义3.1,u*+ε为上解.由引理3.3,u≤u*+ε.引理得证.

定理1.2的证明 令λ∈(λ*,∞).下证问题(2)至少存在两个正解.显然,

-(u*(t))′+a(t)u*(t)=

λ*f(u*(t))<λf(u*(t)),

u*是问题(2)的下解,而u*+ε是问题(2)的上解,由引理3.3,存在问题(2)的解uλ使得u*≤uλ≤u*+ε.因此,当λ>λ*时,存在一个正解uλ且uλ∈Ω,而对于0<λ<λ*正解不存在.

选取I是[λ*-1,∞)上的任意闭区间，满足区间左端点是λ*-1.则

(λ*,∞)∩I≠∅,(0,λ*)∩I≠∅.

下证当λ∈(λ*,∞)∩I时问题(2)的第二个正解存在.

deg(I-Tλ,Ω,0)=1.

另一方面,由引理4.1,当λ∈I时,问题(2)的所有正解都是有界的.因此,当L足够大时有

deg(I-Tλ,B(0,L),0)=m,

其中λ∈I,m为固定常数,B(0,L)是在C[0,T]上以0为心,L为半径的球.由于对所有的0<λ<λ*,问题(2)正解不存在,所以m=0.再由拓扑度的切除性可得

deg(I-Tλ,B(0,L)Ω,0)=-1.

因此当λ∈(λ*,∞)∩I时问题(2)存在第二个正解.定理得证.