紧扣数学本质，深化数学理解

潘灵聪

摘要：数学学习的意义在于理解规则概念、获得方法策略、体验思考价值，感受学习愉悦等。教师应该紧扣数学教学的本质，把学习目标变为任务驱动，回归有意义的数学教学。

关键词：数学本质  数学理解  《三角形三边关系》

小学数学教师需要设立每堂课的教学目标，要基于对教学内容所蕴含的教学价值、思维水平、育人因素进行合理解读，设计有价值的教学活动。当然，教师也需要合理评估学生的能力，制订课堂的动态目标。

《三角形三边关系》是小学数学图形与几何领域的重要内容，教材围绕“通过实验，发现三角形任意两边的和大于第三边”这一教学目标，附带了几组小棒，旨在让学生用小棒拼成三角形，以便完成数学实验。然而，学生不明白为什么要这样做，只是机械地跟随指示进行实验，课堂因此而变得乏味无趣。笔者认为，数学课程应该提倡“淡化形式，注重实质”，让学生经历数学活动的过程，体验数学思考方法的重要性。

一、基于学情现状的重新审视，走近起点，课堂真实自然

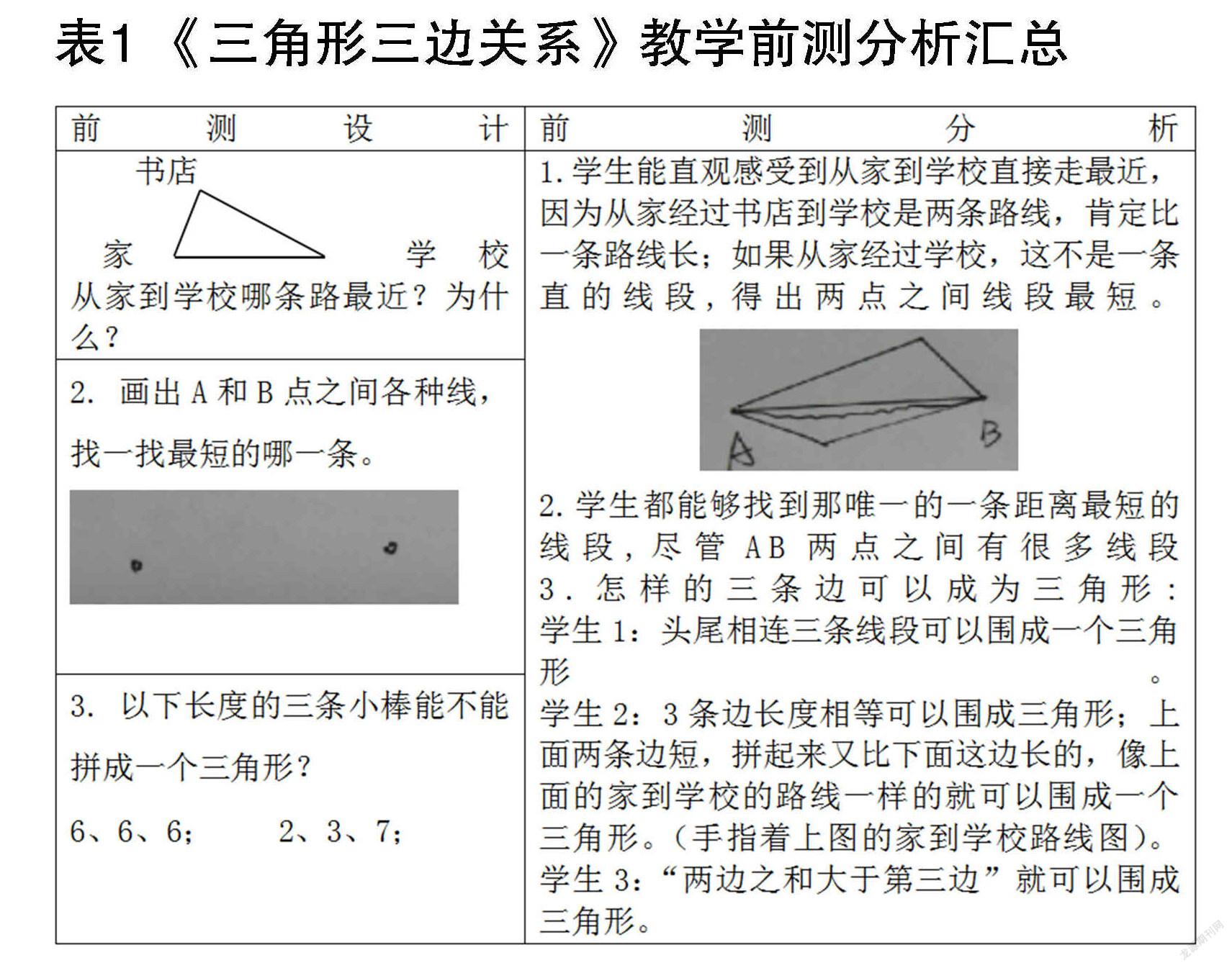
数学学习基于经验，又需超越经验，学生需要有一种理性探究的精神。要想调动学生有意义的学习，教师应该充分考虑学生的能力和经验。基于这样的思考，笔者在课前进行了前测，如表1所示。

在设计前测维度时，教师必须了解学生的原有起点：第一，衔接维度。学生能否联系起“组成三角形”和“两点之间线段最短”两个知识点。第二，知识维度。学生是否了解判断“三条线段能否组成三角形”的一般方法，学生是否知道“三边关系”的理论依据就是“两点之间线段最短”。第三，能力维度。学生能否从三角形三边的一般关系，发现最简便方法，总结出“最短两边之和大于第三边”规律。

（一）改辙易途，对接经验真实自然

制订教学目标时，教师应针对学生的知识基础，结合具体学情，从活动设计方面进行改变，改辙易途，让课堂自然而真实。

片段之一：

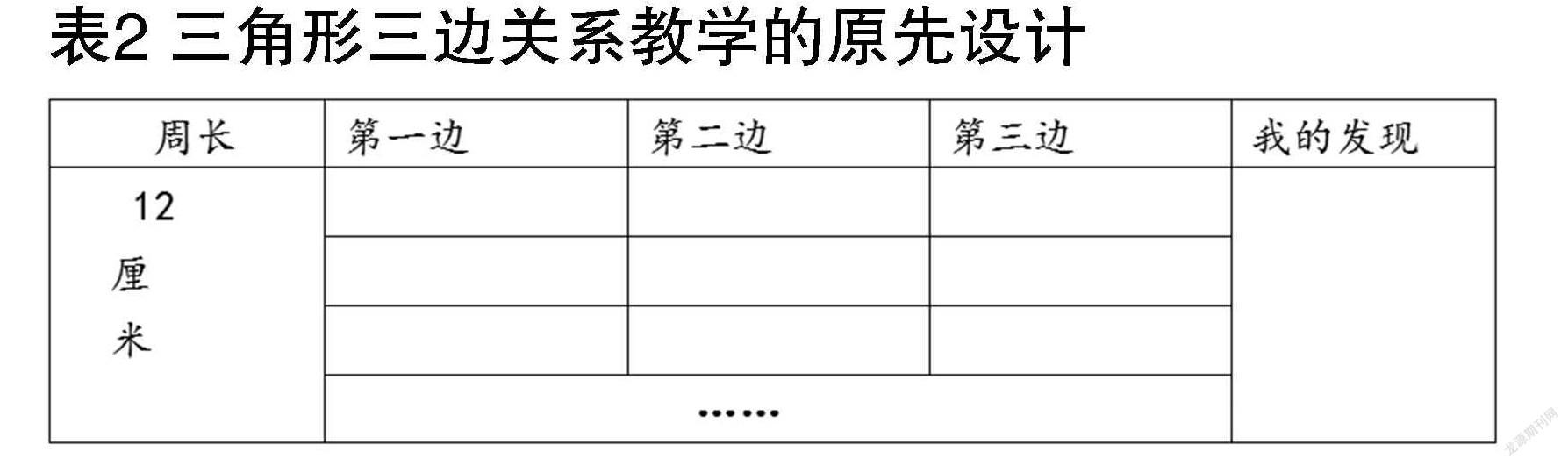
笔者原先是这样安排教学的：出示周长是12厘米形状不同的三角形，并分别量出三条边的长度，如表2所示。

之后，笔者改善了原教学中由三条小棒拼三角形的设计，转而提供周长都是12厘米的三角形，让学生认识到周长一样的三角形，由于三边长度不同，形状也是不同的，改善了原教学只重视可以围成三角形的三边的研究。

（二）固本正源，借力猜想任务驱动

有意义的数学学习需要把目标变为任务，把知识变成问题，把方法变为问题。学生需要经历体验的过程，才能发现和理解三角形三边关系。在以往教学中，教师只是让学生量一量三角形三边的长度，这样的体验空间太小。于是，笔者设计了第二次教学方案。

片段之二：

教师问：“用12厘米的细铁丝围成一个三角形，你觉得三条边的长度可能是多少？（每边长度取整厘米数）”

学生1回答： “4、4、4。”

学生2回答：“3、4、5。”

学生3回答： “1、4、7。”

学生4回答：“ 5、5、2。”

教师可以让学生猜一猜三角形的三边可能会是什么情况，由于是同一根铁丝围成的三角形，总长是相等的，学生理所当然以为无论怎么分，都可以围成三角形。事实上，由于分成不同的长度，有的长度是不可以围成三角形的。教师借助这样的设计，激发了学生深入研究的兴趣。

二、基于核心目标的深度扣问，延伸体验，课堂深入厚实

思考是数学教育的本真，教师要让学生在动态过程中寻找三角形三边本质关系，在冲突中思考，在探究中反思，凸显数学思考的价值取向。

（一）提领而顿，聚焦核心高峰体验

教师要确定课堂核心目标，深挖隐藏在背后的数学思想，帮助学生体验和感悟数学知识。

片段之三：

教师问：“手里的细铁丝按照刚才反馈的每组三条边的长度，折一折、围一围，你发现什么？”

学生1回答：“三条边的总长度相同。”

学生2回答：“有些可以围成三角形，有些不能围成三角形。”

学生3回答：“当两边之和小于第三条边时围不成一个三角形。（课件展示不能围成三角形的三条边）”

学生4回答：“3+4>5，所以能圍成一个三角形。”

在学生反馈以后，教师组织讨论：“同样长的铁丝折成三段，为什么有的三条边可以围成三角形，有的不能？”

数学需要理性的思考，教师要在课堂上充分调动学生思考，通过操作让学生明白内涵，并经过分析充分地表达出来。

（二）本立道生，实现从本到意的突围

教师的课堂教学不应该只满足于知识的传输，更要帮助学生关注知识结构，构建数学思维，把数学思想与方法当作学习的根本，让数学学习彰显数学思想的力量。

片段之四：

教师问：“那7+3>2是不是也可以围成一个三角形？ ”

学生1回答：“好像不行！ ”

学生2回答：“我发现有的三条线段有2组线段之和大于第三条边的。 ”

学生3回答：“我知道，不能只看其中两条边相加的和大于第三边，必须每两边相加与第三边比大小，才可以围成一个三角形。 ”

教师问：“能不能重新概括一下，并完整地说一说其中的规律？ ”

学生4回答：“应该是任意两边之和大于第三边，这样的三条边能组成三角形。 ”

教师问：“三角形任意两边之和大于第三边，还有其他理由来解释吗？ ”

学生5回答：“像上面的三角形中，我们可以把线段AB 看作是A和B之间的距离，A点经过C到B也可以看作A和B之间的距离，我们已经知道了两点之间线段最短，所以BC+AC>AB。 ”

学生6回答：“这样还是不完整的，我们可以把线段AC 看作是A和C之间的距离，A点经过B到C也可以看作A和C之间的距离，我们已经知道了两点之间线段最短，所以AB+BC>AC;同样的AB+AC>BC。 ”

学生7回答：“老师，两点之间的线段长度要比两点之间的折线要短，两点之间线段最短。 ”

教师问：“判断能不能围成一个三角形，看来大家都掌握了，你们能不能改进一下，使得更为方便呢？ ”

学生8回答： “只要最短的两条边的和大于第三边就可以了。 ”

由于同样长的铁丝可以分成不同的长度，出现不同的结果，学生会发现能围成三角形的有两边之和大于第三边，不能围成三角形的也有两边之和大于第三边，发现“最短的两边之和大于第三边”的规律。这样，学生不仅收获了数学知识，还充分运用了数学思想，实现了课堂教学从本到意的突围。

（三）追本求源，由表及里顺势而为

数学课堂是一个动态的过程，蕴含着数学本质的关键点，教师应该引导学生寻找思维源头，由表及里，实现有意义的数学学习。

片段之五：

教师问：“把一根长15厘米的铁丝折成一个三角形，最长的一段铁丝应该是多少，你是怎么想的？ ”

学生1回答：“15除以3是5，比5多1就是6厘米。 ”

学生2回答：“不对，那我比6厘米多一点，7厘米也可以吧。 ”

学生3回答：“那8不可以吗？ ”

学生4回答：“如果是8厘米的，剩下还有7厘米，那这个三角形算3、4、8厘米，根据刚才学的两条短边之和大于最长边，3+4<8。 ”

教师问：“学生非常会思考，那么最长这条边应该满足怎样的要求呢？ ”

学生5回答：“我觉得把15厘米先分成两段，分别是8厘米和7厘米，7厘米作为最长边， 再把8厘米分成两条短边就可以了。 ”

教师问：“这位学生讲得非常有道理，想想可以是哪些三角形？ ”

学生7回答：“如1、7、7，或2、6、7，或3、5、7。 ”

教师让学生讨论“一根铁丝折成一个三角形，最长一段是多少”，可以启发学生总结出“两条短边之和大于第三边”的规律，并感悟到最长的边虽然要比另外两条边长，但不能大于它们的和。教師不断启迪学生的思维，让课堂有了别样的精彩。

三、基于学习差异的现实存在，求同存异

学生都是不同的生命体，有着各自不同的思考方式，教师不能用相同教学目标评价学生，应该直面学生存在的差异。

片段之六：

教师用两根长度分别是4厘米和5厘米的小棒围成一个三角形，问学生：“第三条边最短可能是多少，最长可能是多少？”

刚刚还沉浸在发现“两条短边之和大于第三边就能组成一个三角形”这个规律之中的学生，又重新进入新的思维状态。

学生1回答：“把5作为长边，想4+（ ）>5 ，4+2>5所以最短的为2。 ”

学生2回答：“把5作为长边，那么5-4=1，这样短的两边刚好与长边一样，这样不能拼成一个三角形，所以1再增加1厘米就可以拼成一个三角形，于是5-4+1=2厘米。 ”

学生3回答：“把未知这条边看作最长边，那么  4+5>（   ），最长可以是8。 ”

学生4回答：“把未知这条边看作最长边，那么已知的4和5作为短边，根据两条短边之和大于第三边，所以4+5=9，再减少1厘米就可以成为三角形 4+5-1=8厘米。 ”

设置这样的问题具有挑战性，由于学生的认知方式不同，会存在客观的个体差异。教师要接受这种差异，不用整齐划一的标准衡量学生，给予不同学生不同的评价标准。

参考文献：

[1]曾娴秋.指向数学深度学习的进阶性大问题设计研究——《三角形的三边关系》教学设计研究[J].新智慧，2021（4）.

（作者单位：浙江省台州市天台县赤城街道第二小学）