区间二型T-S模糊研究综述

王文庆，孙丽花

(西安邮电大学 自动化学院，陕西 西安 710121)

Zedeh在1965年提出了一型模糊集，也称为传统模糊集[1]，其在高度不确定的情况下无法获得较好的效果。为了提高系统处理不确定性的能力，Zedeh 在1975年提出了二型模糊集的概念[2]。二型模糊集的隶属度不是确定值，而是表现为一型模糊集。二型模糊集在提出之时，由于计算代价太大并未得到太多的重视，直到Mendel等[3]提出二型模糊集的简化计算，二型模糊集及系统才得到了学者们的关注。近些年来，二型模糊集及系统理论逐渐成为学术界的热点问题，已广泛应用于理论研究和控制领域的实际应用中。特别是在工业系统控制中，该理论对于复杂系统的处理具有很大优势。T-S模糊模型具有逼近任意光滑非线性函数的良好能力，并且具有局部线性化的性质，而二型模糊集可以提高处理不确定性的能力。将二型模糊集和T-S模糊两者结合成二型T-S模糊系统，可以提高处理不确定和非线性的能力。

该研究主要从两个方面对区间二型T-S模糊控制进行介绍，首先对区间二型模糊集进行概述，再介绍区间二型T-S模糊控制，对区间二型T-S模糊控制研究状况进行论述。最后，给出关于区间二型T-S模糊控制的总结和展望。

1 区间二型模糊集

1.1 基本概念及应用

一般二型模糊集是三维空间的集合，以论域元素、主隶属度和次隶属度为三维坐标轴，而区间二型模糊集是在一般二型模糊集的基础上，将次隶属度恒定为1，因此区间二型模糊集是普通二型模糊集的特殊版本。区间二型模糊集与一般二型模糊集相比计算简单，并且保留了二型模糊集处理不确定性的能力，因此区间二型模糊集在实际应用中更多。区间二型模糊集中比较重要的概念包括上隶属度函数、下隶属度函数、不确定覆盖域和嵌入一型模糊集[4]。

区间二型模糊集的表示定理指出，不确定覆盖域是所有嵌入一型模糊集的并集。定理指明所有关于二型模糊集合模糊系统的运算，例如区间二型模糊系统推理计算和降型、两个区间二型模糊集之间的相似度等，这些都需要考虑嵌入一型模糊集，而王飞跃等[5]采用集合形式描述了二型模糊集的特征并简化了其表述。根据二型模糊集的新定义，将二型模糊集分为离散型、半连通型、连通性及复合型，并列出了不同类型二型模糊集的表达方法。

构造模糊集是模糊理论的重要研究之一，目前专门研究区间二型模糊集构造的方法尚未完善，缺乏指导准则。常用的方法包括利用专家经验和知识法、利用区间二型模糊C均值聚类法、区间法以及加强区间法等，其中区间法、加强区间法适用于区间型数据。刘帅[6]针对构造区间二型模糊集方法存在的问题，提出了一种具有适用于常见的点集和加权点集，不受模糊因子影响，以及能够结合数据自身特征和专家经验优点的区间二型模糊集构造方法。这种方法基于平衡粒原则，先利用目标数据集通过优化的方法构造一型模糊集，再将一型模糊集扩展成区间二型模糊集。

随着越来越多的构造方案的提出，区间二型模糊集的应用也越来越广泛。邵东国等[7]提出基于贝叶斯模式平均与区间二型模糊集的分区灌溉方法，基于区间二型模糊集理论对各地下水埋深区域的灌溉制度进行综合评价，将区间二型模糊集应用在灌溉上。文献[8]利用区间二型模糊C均值聚类算法，解决遥感影像的复杂模糊性对影像变化检测结果的干扰问题，提出改进的区间二型模糊聚类的方法。利用区间二型模糊集可以进行语义分析，构建评价模型[9]，也可以用区间二型模糊集表示一个概率语言术语集，在绿色供应商选择中进行运用[10]。区间二型模糊集还可以应用在风险决策[11]、投资组合[12]和生物模型[13]等各个方面中。

1.2 区间二型模糊系统

使用至少一个区间二型模糊集的模糊逻辑系统便可称为区间二型模糊系统，其结构示意图如图1所示。

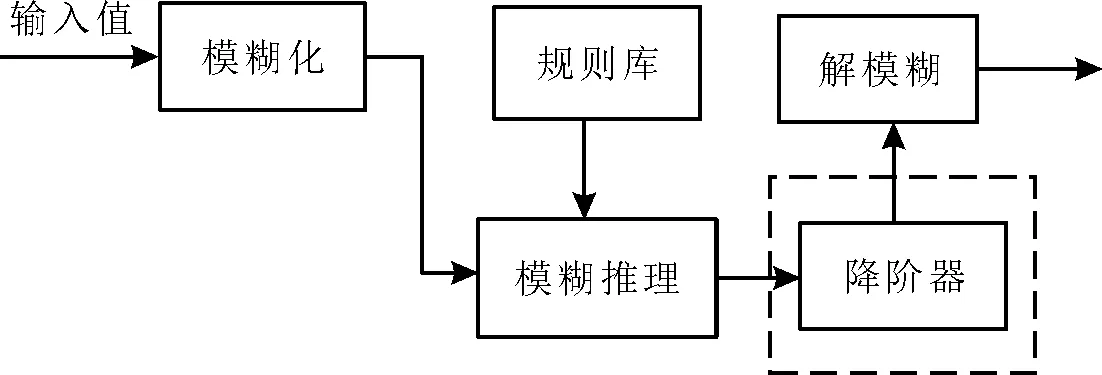
图1 区间二型模糊系统结构示意图

区间二型模糊系统和一型模糊逻辑系统结构相似，唯一的区别在于区间二型模糊系统有一个降阶器，对经过模糊推理后的区间二型模糊集转换成一型模糊集，最后进行解模糊。也有学者把降阶器和解模糊放在一起，直接将推理机输出的区间二型模糊集映射为一个明确的输出。

二型模糊系统比传统模糊系统更复杂，主要表现在二型模糊系统需要进行降型，最早的降型算法是由Karnik等[14]提出的KM(Karnik-Mendel)迭代降型算法。但是KM降型算法的迭代运算量较大，系统运算负担较重。Mendel针对对称区间二型模糊集,提出的新的质心计算方式，减少了一半的计算量。随后，越来越多的降型算法被提出。Wu和Mendel提出的WM降型算法可以减轻区间二型模糊控制器的负担[15]，张超龙等[16]提出区间二型模糊比例积分(Proportional Integral，PI)控制器解析结构的方法。陈阳等[17]在广义二型模糊集的α平面表达理论，提出一类二分搜索KM算法完成了广义二型模糊逻辑系统质心降型。而后又通过数值分析技术中牛顿-科特斯求积公式将KM算法扩展成3种不同形式的加权KM算法，提出了基于加权KM算法的区间二型模糊集质心计算的方法。刘显亮等[18]提出了新的算法计算区间二型模糊集的质心，二进制算法和扩展二进制算法的有效性通过大量实验也被证实。

区间二型模糊系统的应用最广泛的领域莫过于控制领域了，工业系统控制中处理复杂系统区间二型模糊系统具有很大的优势。工业生产中，区间二型模糊系统可以应用在甲烷氧化过程中[19]、水位的控制[20-21]和青霉素发酵[22]等方面。区间二型模糊系统还可以应用在机器人控制中，将区间二型模糊系统和滑模控制器组合，设计一种区间二型模糊滑模控制系统[23-26],也可以设计一种区间二型模糊PID(Proportional Integral Derivative，比例积分微分)控制器[27-28]，应用在二型精馏塔的控制中。Ahmad 等[29]用低成本单片机实现区间二型模糊PID控制系统。Ashraf等[30]提出一种新型的区间二型模糊供应上管理库存系统，将区间二型模糊集表示需求和订单数量，并利用粒子群优化的方法解决模型方案。文献[31-32]将区间二型模糊系统应用在现场可编程逻辑门阵列(Field Programmable Gate Array，FPGA)，与硬件设备结合，增加了区间二型模糊系统的实用性。此外，区间二型模糊系统也广泛应用在图像处理、模式识别等领域中。

2 区间二型T-S模糊系统

T-S模糊模型规则后件是线性表达式，可以用来表示线性子系统，一系列的局部线性子系统结合模糊隶属度函数可以表示为非线性系统全局的输入输出关系，因此可以说T-S模型是非线性系统的局部线性化的描述方法，被广泛用于非线性系统的建模与控制。

2.1 基本规则与全局模型

区间二型模糊系统具有处理不确定性的能力，而T-S模糊模型具有局部线性化的能力，将两者结合生成区间二型T-S模糊系统，相比于一型T-S模糊系统，增加了处理不确定性的能力。 二型T-S模糊模型不仅保留了一型T-S模糊模型的优点，而且还增加了处理不确定性的能力。区间二型T-S模糊模型用IF-THEN规则可描述为

Rulei:IFg1(x(t)) isH1i，andg2(x(t)) isH2i，… andgk(x(t)) isHki.

THEN

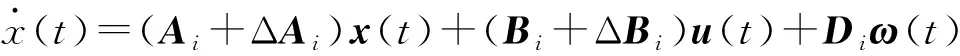
式中：Hki是前件变量gk(x(t))(k=1,2,3,…,n)在第i(i=1,2,…,n)条模糊规则下的模糊集；x(t)、u(t)、Z(t)和ω(t)分别为系统状态向量、控制输入向量、输出向量和干扰向量，且ω(t)∈L2[0,∞]；Ai、Bi、Ci、Di和Fi是适当维数的常数矩阵；ΔAi和ΔBi为具有不确定性的参数矩阵，且[ΔAi,ΔBi]=GiF(t)[EAi,EBi]，其中Gi、EAi和EBi为已知矩阵，F(t)为未知矩阵，且满足FT(t)F(t)≤I，I为单位矩阵。

第i个模糊规则的激活强度为

其中，

表示gk(x(t))的上下隶属函数，并且

即gk(x(t))的上隶属度函数在下隶属度函数的上方。

区间二型T-S模糊系统全局模型描述为

其中，

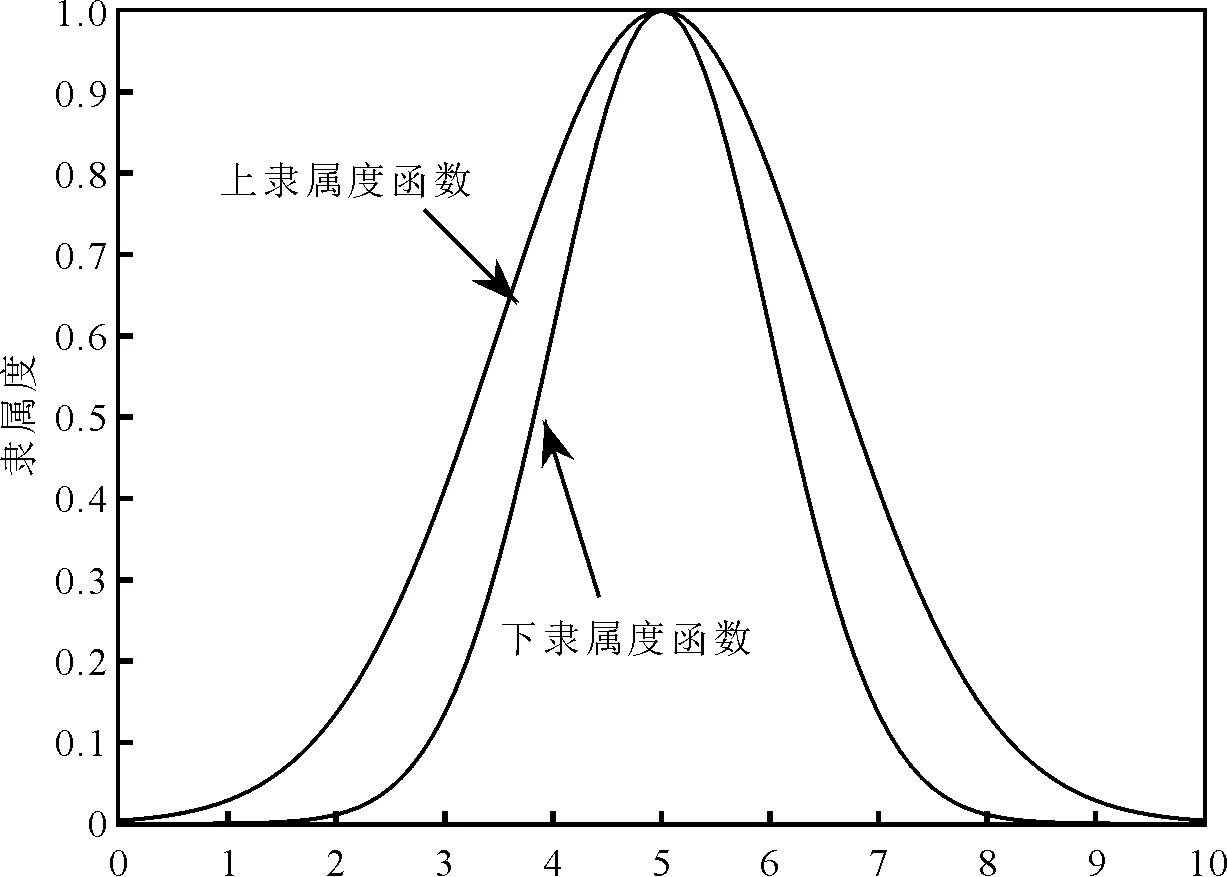
图2 上、下隶属度函数

区间二型T-S模糊模型不但可以用来表示参数不确定性的非线性系统，也是设计区间二型模糊控制器的工具。可以把无数个具有确定隶属函数的一型T-S模糊模型的集合看成是区间二型T-S模糊模型，因此区间二型T-S模糊模型处理不确定的能力比一型T-S模糊模型处理能力更强。

2.2 研究进展

目前，关于区间二型T-S模糊系统的相关问题的研究主要有稳定性分析、控制器设计和工程应用等3个方面。

2.2.1 稳定性分析

稳定性是系统的基本结构特性，也是系统能够正常工作的前提，因此研究系统的稳定性至关重要。模糊李雅普诺夫函数可以降低稳定性分析的保守性，推导基于区间二型T-S模糊模型控制系统的稳定性条件[33]。工农业生产、生活等各个领域，大量存在时变控制系统，因此时滞现象不可避免。时滞的存在可能会增加系统的不确定性，这种不确定性又可能会引起整个系统的不稳定或者产生震荡，因此时滞使得系统分析更加复杂，对于系统时滞性的研究具有重要的实际理论和应用价值。文献[34-37]对时滞的系统进行了研究，对于系统中存在的网络时滞，利用Lyapunov-Krasovskii泛函方法，设计闭环系统渐近稳定的状态反馈控制器，解决区间二型T-S模糊模型网络化系统含有时变时滞的镇定问题。通过建立具有上下级隶属度综合信息的多增益控制器，提高了稳定性条件的可解性，进而研究二型T-S模糊系统的鲁棒稳定性问题[38]。对于可靠样数据控制系统的稳定性问题，不同于之前的研究，文献[39]考虑到整个采样区间的信息与增广状态向量的关系，设计区间二型T-S模糊系统的可靠采样数据控制。通过对离散区间二型模糊控制系统稳定条件的研究，可以将区间二型T-S模糊模型用于表示受不确定性影响的非线性系统[40]。文献[41-42]研究了离散二型T-S模糊系统的稳定性分析，但获得结果依赖于特殊类型的隶属函数，文献[43]在文献[41-42]的基础上研究了连续二型T-S模糊控制系统的稳定性分析。

2.2.2 控制器设计

研究区间二型T-S模糊模型的控制问题至关重要，提出合适的控制方案才能设计更好的控制器，实际应用也会更简便。基于区间二型T-S模糊模型，针对有限带宽、多扰动的非线性网络系统，Yazmin等[44]提出一种事件触发的扰动和抑制的控制方案，通过减少控制器更新的频率，节省了网络资源。文献[45]和文献[46]都研究有限时间控制，而文献[45]研究了具有范数有界不确定性和时变时滞的区间二型T-S模糊系统的有限时间控制，利用隶属函数依赖的分析方法，将上下隶属函数的信息集成到稳定条件中，减少了保守性。文献[46]研究了不连续互联系统的有限时间分散控制问题，利用区间二型T-S模糊模型，提出一个统一的二型T-S模糊互联系统，利用有限时间镇定理论和广义Lyapunov泛函方法进行分散控制。针对一类具有非线性输入输出关系的非线性系统，基于二型模糊系统理论，王占山等[47]提出区间二型和T-S型模糊控制器相结合的模糊控制方法。陈洪军等[48]研究了系统参数不确定的区间二型T-S模型网络系统在拒绝服务(Denial of Service，DOS)攻击下的安全控制问题。对于模糊脉冲控制的问题，文献[49]提出了区间二型T-S 模糊脉冲控制方法。自适应逆控制是一种非线性系统控制方法，现已被广泛研究。高娟娟等[50]提出了一种基于区间二型T-S模糊系统的自适应逆控制方法，可以实现对复杂非线性系统的有效建模与控制。李一民等[51]提出区间二型T-S间接自适应模糊控制，系统的规则前件是区间二型模糊集合，后件为精确数，这种控制方法减少了规则不确定对于系统的影响，提高了系统的精度，同时也减少了系统的规则数。

状态反馈控制在实际中的应用通常不可测量或者测量代价太高，因此研究输出反馈控制在实际应用中具有重要的意义。针对外部动态，采用区间二型T-S模糊模型逼近具有多个时变时滞和外部扰动的不确定系统，进而研究区间二型T-S模糊多时变时滞系统的鲁棒H∞动态输出反馈控制[52]。而对于静态输出反馈控制系统，利用普通二次李雅普诺夫函数，可以得到隶属函数形状独立镇定的条件，以及区间二型模糊系统的静态输出反馈控制[53]。针对具有范数有界不确定性和时变时滞，设计一种静态输出反馈控制器可以用来控制系统的有限时间稳定性[54]。

预测控制是一类利用计算机实现的先进的控制算法，具有处理约束优化控制问题的能力，在工业界和学术界也有了广泛的关注。针对圆罗宾协议下研究一类区间二型T-S模糊系统的模糊模型预测控制问题，将圆罗宾协议和二型T-S模糊系统建立统一的表示，生成一个新的网格化二型T-S模糊系统[55]。对于非线性系统的预测控制问题，可以采用区间二型T-S模糊模型描述非线性系统，设计一种模糊预测控制器，也可以利用一种基于二型T-S模糊及粒子群优化的预测控制算法，利用混沌粒子群优化算法，避免非线性预测控制中复杂的各种计算，也能快速搜索最优解[56]。

输出反馈预测控制的研究，大都是利用区间二型T-S模糊模型在非线性网络控制系统中，采用马尔可夫链描述系统中的随机丢包，建立数学模型。文献[57]研究了区间二型T-S模糊模型描述的非线性网络控制系统动态输出反馈模型预测控制，不同的是该文献采用伯努利二进制分布，描述非线性网络系统中的丢包过程。对于区间二型T-S模糊系统的输出反馈模型预测控制进行研究，可以设计离线的状态观测器，估计真实状态和预测未来，估计误差集的界限和优化控制器的增益。不同的是文献[58]在马尔可夫丢包的描述系统中，而文献[59]研究了具有有界扰动的区间二型T-S 模糊系统的输出反馈模型预测控制。针对存在有界扰动和数据丢失的问题，利用区间二型T-S模糊模型建立非线性网络控制系统模型,提出了一种基于状态观测器和自适应触发方案的模型预测控制[60]。对于误差处理，利用区间二型T-S模糊模型对参数不确定的非线性对象进行描述，构建在线更新误差椭圆集合的基本方法[61]。而考虑具有量化误差和马尔可夫数据丢失的区间二型T-S模糊系统的模型预测控制，利用马尔可夫跳跃模型处理数据丢失，扇区边界方法处理量化误差[62]。

基于区间二型T-S模糊模型设计模糊控制器，常用于非线性系统中。针对于区间二型T-S模糊系统处理的参数不确定的非线性系统，提出一种根据系统状态的值，进行切换的区间二型区域切换模糊控制器[63]，考虑了上下级隶属函数的信息，减少了稳定性中的保守性。在区间二型T-S模糊模型表示的参数不确定性的非线性时滞系统，在统一框架下设计了系统的滤波器问题[64]。对于系统的有限时间自适应时间触发耗散滤波问题，区间二型时滞T-S模糊网络马尔可夫跳变系统，在设计过程中考虑了模糊滤波器的因素，建立一种自适应时间触发机制[65]。在多性能指标框架下，文献[66]研究了区间二型T-S模糊时变时滞系统的滤波器设计，提出前提隶属函数不匹配的区间二型模糊滤波器，通过矩阵解耦将滤波存在条件表示为线性矩阵不等式。文献[67-68]都对于故障检测滤波设计进行了研究，文献[67]对基于区间二型T-S模糊模型的非线性系统，提出了一种新的隶属函数相关的有限频率故障检测滤波设计方法。文献[68]研究有限频率下离散时间区间二型T-S模糊系统的故障检测滤波设计，利用离散时间傅里叶变换，对有限频率进行分析，建立了离散区间二型T-S模糊系统的滤波器。

2.2.3 工程应用

模糊系统最早被用于锅炉和蒸汽机的控制中，随着科技的发展，T-S模糊控制是基于模型的模糊控制的重要方法，也是非线性系统中常用的工具。模糊系统作为通用逼近器也已经成功运用在模糊控制中，文献[69]分析了模糊系统作为通用逼近器性能及影响因素，讨论改进其结构参数的新方法，并分析了模糊系统研究的热点问题及研究发展方向。目前，已有较多关于一型T-S模糊系统的研究成果，但关于二型T-S模糊模型的应用还不是很多，还需要进一步研究。文献[70]提出一种基于量子蜂群聚类的T-S建模方法，并在智能发电运行控制系统中应用。将优化算法和T-S模糊结合的还有文献[71]，粒子群优化和支持向量机与区间二型T-S模糊系统进行结合，设计了一种分类系统用于性别识别，利用模糊迭代自组织数据分析技术和粒子群优化学习模糊系统前件参数，后件参数通过支持向量机进行学习。利用模糊模型设计分类系统的还有，将神经网络和加权模糊隶属度和T-S模糊模型结合，对健康人和帕金森病(Parkinson’s Disease，PD)患者进行分类[72]。

模糊控制也被广泛应用到永磁同步发电机的研究中。对于永磁同步发电机中的非线性系统，多数研究采用模糊模型进行处理，文献[73]将区间二型T-S模糊系统应用到永磁同步发电机的电流控制中，采用二型T-S模糊系统处理永磁同步发电机系统中的非线性问题。文献[74]采用自适应T-S模糊模型对永磁同步发电机的非线性系统进行表征，在水动力涡轮系统中进行运行。文献[75]也采用T-S模糊理论将非线性模型转换为线性子模型，设计了模糊记忆采样数据控制器，研究非线性永磁同步发电机风力机系统的镇定分析。

在工业上，除了文献[76]研究了二型T-S模糊系统在球磨机料位预测中的应用，即用二型模糊逻辑对球磨机料位进行表示，建立了基于区间二型T-S模糊系统的球磨机料位预测模型。利用模糊C均值算法提取前件参数，通过反向传播算法对前件参数进行调整，最小二乘法对后件参数进行辨识。还有文献[77]采用T-S模糊模型，设计一种跳汰机排料系统，解决实际工业系统中的时滞性、非线性等问题。

3 总结与展望

区间二型T-S模糊模型，既有二型模糊集处理不确定性的良好能力，又具有T-S模糊模型万能逼近的性质和局部线性化良好性质。因此，相比于一型T-S模糊模型不能处理高度不确定的系统，研究二型T-S模糊模型，不仅在理论研究上而且在实际应用中，都具有更重要的价值和意义。通常利用区间二型T-S模糊模型对受参数不确定性影响的非线性系统进行建模，对于时变时滞的系统，基于区间二型模糊系统的也有一些研究。通过概述区间二型模糊集合、区间二型模糊系统、区间二型T-S模糊模型和区间二型T-S模糊系统的控制，可以看到目前关于区间二型模糊集的研究已经有不少成果，但是对于区间二型T-S模糊的研究还需要进一步研究。

虽然区间二型T-S模糊模型要比一型T-S模糊模型处理不确定性能力强，但区间二型模糊模型也要更加复杂，模型简化是降低高阶复杂系统的阶来实现。有文献对离散时间区间二型模糊系统进行降价，而对于区间二型T-S模糊模型的简化问题的研究仍然处于空白。因此研究区间二型T-S模糊模型的简化问题有待进一步研究。

目前，基于一型T-S模糊模型的研究已经取得了较多的成果，但基于二型T-S模糊模型的研究仍存在大量的研究课题。有文献已经对二型T-S模糊模型的稳定性、鲁棒性进行研究，也有不少文献研究模型预测控制问题和控制器设计，但仍然需要扩展区间二型T-S模糊模型的应用方向，因此将区间二型T-S模糊系统与实际工程结合也是待解决的问题。

随着神经网络、进化计算等方法的研究深入，将深度学习、强化学习和卷积网络等机器学习算法应用于二型T-S模糊系统，训练其后件参数是一个非常有价值的研究方向。神经网络权值学习的很多方法可以移植到二型T-S模糊推理系统的参数训练上。而进化计算的全局优化算法，如遗传算法、蚁群算法和粒子群算法等，则可用于二型T-S模糊系统的结构优化与参数寻优。进一步将人工智能(Artificial Intelligence，AI)工具与二型T-S模糊系统深度融合，构建多层次、智能化的模糊神经大数据挖掘系统也是非常值得期待的研究方向。

模糊系统从其诞生之初就致力于处理人类系统中的不确定性问题，区间二型T-S模糊系统的研究也离不开这一方向。在词计算、语义挖掘等方面，一型模糊系统已有研究基础，而二型模糊系统的研究还方兴未艾。充分利用区间二型T-S模糊系统在处理高不确定性问题上的优良特性，研究其在词计算规则，自动从数据中归纳总结模糊语义的模式和结论，以期助力于机器和人类的交流理解，也是二型模糊系统未来重要的研究方向。