各向异性介质界面模式转换波II:仿真验证
法 林,王家乐,赵 琳,李玉霞,邹 骁,胡凯利,李 晓,张晓琳,法晓雪,赵梅山
(1.西安邮电大学 电子工程学院,陕西 西安 710121;2.西安翻译学院 信息工程学院,陕西 西安 710105;3.中国石油集团测井有限公司 陕西 西安 710061;4.莒县发展和改革局 山东 日照 276599;5.长庆石油分公司 伴生气综合利用项目部,陕西 西安 710021;6.芝加哥大学詹姆斯·弗兰克研究所 化学系 伊利诺伊 芝加哥 60637)
地震勘探数据振幅随偏移距变化(Amplitude Variation with Offset,AVO)的反演分析是寻找地球内部资源的一项重要技术。这一技术在近年来逐步发展成熟,例如,文献[1]采用文献[2]给出的模式转换波极化符号规则研究了各向同性地层界面的反射率,以进行地震勘探数据的AVO反演分析;一些学者针对实际地层的不同状况,研究了地层的反射特性[3-6]。在地球物理勘探过程中,绝大数地层都具有一定程度的宏观各向异性,并且地层的这种宏观各向异性大多表现出横向各向同性的特点,可以采用六方晶系的刚度系数矩阵来描述其力学特性[7-8]。基于对地层各向异性的研究成果[9-11],文献[7]提出了地震波的射线追踪理论,文献[8]研究了真实各向异性地层的波场,提出了在考虑地层各向异性的情况下的地震勘探数据的AVO反演分析技术[12]。文献[13-16]报道了与先前理论预测有关的分析和数值研究。然而,针对在两种不同各向异性介质界面上产生的模式转换波的极化状态的复杂计算还有待进一步研究。
文献[17]对各向异性介质界面模式转换波进行了理论分析,研究了各向异性介质界面的反射/折射特性,以及各向异性介质界面上产生的模式转换波的极化等现象,并且为各向异性地层中测量地震勘探数据的精确AVO反演分析时间域—深度域转换提供了理论依据。
在文献[17]的基础上,拟进一步对各向异性介质界面的模式转换波进行仿真验证。应用实际测量岩样各向异性参数和物理参数,构造折射介质具有不垂直对称轴的各向异性页岩-泰勒砂岩界面和各向异性页岩-油质页岩界面两种具有垂直对称轴和倾斜对称轴的横向各向同性(Transverse Isotropy with a Vertical Axis of Symmetry-Transverse Isotropy with a Tilted Axis of Symmetry,VTI-TTI)介质界面。计算在这两种界面上产生的模式转换波的慢度曲线和极化状态以及界面的反射/折射特性,对仿真结果进行分析和比较,以及合理的解释。
1 模型构建
构造两个界面系统,一个是各向异性页岩-泰勒砂岩界面,另一个各向异性页岩-油质页岩界面。为了讨论和分析方便,定义各向异性页岩-泰勒砂岩界面为系统I,各向异性页岩-油质页岩界面为系统II。构成系统I和系统II岩石的各向异性参数和物理参数如表1所示[10-11]。其中,ρ表示岩石的密度,参数α和β分别表示岩石对称轴方向的P波(Primary Wave)和SV(Shear Vertical)波的相速度,ε、δ和γ分别为VTI介质的各向异性参数。

表1 各向异性页岩、油质页岩和泰勒砂岩的相关参数
各向异性页岩、油质页岩和泰勒砂岩地层的刚度系数矩阵可以表示为[9]
式中,cjh(j,h=1,2,…,6)表示岩石地层的弹性常数分量,其计算表达式分别为[10]
c13=
(1)
c33=ρα2
(2)
c11=(2ε+1)ρα2
(3)
c44=ρβ2
(4)
c66=(γ+1)2ρβ2
(5)
依据表1的各向异性参数和物理参数,由式(1)—式(5)可以得到各向异性页岩、泰勒砂岩和油质页岩等3种VTI介质地层的刚度矩阵。然后,利用Bond变换[17],即可得到TTI折射介质泰勒砂岩和油质页岩的刚度矩阵。
2 仿真及分析
在两个不同VTI-TTI界面中,利用仿真工具MATLAB,对其所有模式转换波的慢度、各向异性参数、极化系数和质点位移反射/折射系数的关系、入射波/反射波/折射波的极化状态性能进行仿真和分析。
2.1 入射波和模式转换波的慢度
作为相速度的倒数,慢度提供关于具有不同物理参数和各向异性参数的地层分层性质的重要信息[18]。 在理论方面,一些VTI-TTI界面系统似乎有一个对应折射SV波的入射临界角,即第二入射临界角,但是,实际上该第二入射临界角却并不存在。对于该问题,还有待进一步进行科学解释。
分析在界面系统I和界面系统II这两个不同VTI-TTI界面产生的模式转换波的慢度。显然,界面系统I和界面系统II的入射介质均为各向异性页岩,且均为VTI介质。泰勒砂岩和油质页岩分别为界面系统I和界面系统II的折射介质,两者均为TTI介质。根据文献[17]中求解相速度的计算公式和表1所示的3种岩石的各向异性参数和物理参数,取TTI折射介质的倾斜角φ=30°,仿真出涉及到界面系统I和界面系统Ⅱ的慢度,P波和SV波的慢度曲线仿真结果如图1所示。其中,θ为在无限大各向异性地层中的P波和SV波的相速度方向与垂直轴之间的夹角,θ(0)为P波入射到VTI-TTI界面的入射角。图1(a)和图1(c)均为以θ为自变量的慢度曲线。图1(a)和图1(c)中的曲线①和曲线③分别为在无限大各向异性页岩中P波和SV波的慢度曲线。图1(a)中的曲线②和曲线④分别为在无限大泰勒砂岩中P波和SV波的慢度曲线。图1(c)中曲线②和曲线④分别是在无限大油质页岩中P波和SV波的慢度曲线。图1(b)和图1(d)均为以入射角θ(0)为自变量的入射P波和在VTI-TTI界面上所有模式转换波的慢度曲线。点A和点B表示入射临界角对应的慢度。图1(b)中的曲线①和曲线③分别为在界面系统I中产生的反射P波和反射SV波的慢度曲线,曲线②和曲线④分别对应的折射P波和折射SV波的慢度曲线。图1(d)中的曲线①和曲线③分别为在界面系统II中产生的反射P波和反射SV波的慢度曲线,曲线②和曲线④分别对应折射P波和折射SV波的慢度曲线。
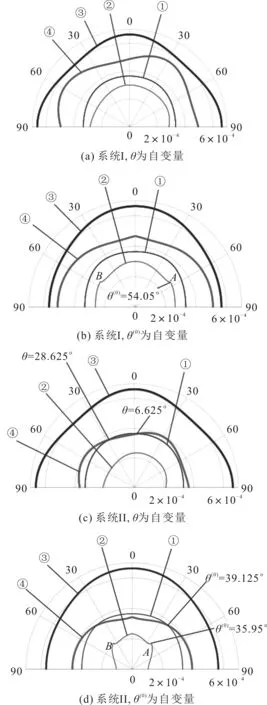
图1 P波和SV波的慢度曲线仿真结果
图1显示,界面系统I和界面系统II在入射介质中的反射P波的慢度曲线相同,即图1(b)的曲线①和图1(d)的曲线①相同。同样,两个界面系统中的反射SV波的慢度曲线也相同,即图1(b)的曲线③和图1(d)的曲线③相同。对于VTI-TTI介质界面上产生的折射P波和折射SV波,每种波的慢度曲线特性均由TTI介质的物理特性和各向异性以及倾斜角等几何结构决定。比较界面系统I的各向异性页岩-泰勒砂岩界面与界面系统II的各向异性页岩-油质页岩界面发现,这两个系统具有其各自不同的特征。值得注意的是,一个系统是否存在入射临界角可能只取决于界面两侧介质的物理性质,例如,若P波入射角θ(0)小于P波反射角θ(2),则可能存在对应折射P波的入射临界角,即第一入射临界角;反之,若θ(0)>θ(2),则系统可能不存在任何入射临界角。
对于折射P波,如图1(b)中的曲线②和图1(d)中的曲线②,界面系统I和界面系统II的入射临界角的位置B显示出了显著折射特征。界面系统I的特征折射点B对应的入射临界角为54.05°,界面系统II的特征折射点B对应于的入射临界角为35.95°。
为了更好地理解各向异性地层界面出现的有关入射临界角的物理现象,以界面系统II各向异性页岩-油质页岩界面为例,分析和讨论折射P波的慢度曲线。图1(d)显示在入射P波的慢度曲线(曲线①)和折射SV波之间的慢度(曲线④)之间的39.125°处存在一个交叉点。
图1(a)和图1(c)还表明,无限大各向异性页岩VTI介质内的P波和SV波的慢度曲线(曲线①和曲线③)关于垂直轴对称,而无限大泰勒砂岩和油质页岩TTI介质内的P波和SV波的慢度曲线(曲线②和曲线④)仅关于不平行于垂直轴的对称轴对称。
观察图1(b)和图1(d)后还可以发现,在VTI-TTI界面上产生的折射P波和折射SV波的慢度曲线关于垂直轴对称。其原因是,入射介质其对称轴为垂直轴的VTI介质,具有特性[18]

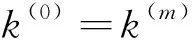
界面系统II中的P波反射角的正弦sinθ(2)以及SV波折射角的正弦sinθ(4)与入射角θ(0)之间的关系的仿真结果如图2所示。

图2 系统II中sinθ(0)和sinθ(4)与θ(0)之间的关系
图2(b)表明,在入射角θ(0)=39.125°处存在折射SV波的正弦和入射P波正弦的交叉点P3。在入射角θ(0)<35.125°的入射角区域,折射SV波的相速度大于入射P波的相速度;在入射角θ(0)=35.125°处,油质页岩中折射SV波的相速度等于各向异性页岩中入射P波的相速度;在入射角θ(0)>35.125°的区域内,折射SV波的相速度小于入射P波的相速度。虽然入射角θ(0)=35.125°接近但不等于折射P波对应的第一临界角θ(2)=35.95°。在整个入射角θ(0)∈(0°,90°)的区域内,都存在sinθ(4)<1,由此可以得出结论,界面系统II各向异性页岩-油质页岩不存在对应折射SV波的入射临界角(即第二临界角)。θ(0)=39.125°的入射角既不是第一临界角,也不是第二临界角。另外,由于界面系统的折射TTI介质中P波的相速度大于入射VTI介质中P波的相速度,所以仅存在第一临界角。
2.2 地层各向异性参数对其入射临界角的影响
为了分析界面两侧地层介质的各向异性和TTI折射介质倾斜角对界面系统的入射临界角的影响,与界面系统I类似,构建一个改进的Daley-Hron各向异性地层界面模型[19-20]。改进的Daley-Hron各向异性地层界面模型的参数如表2所示。其中,φ为TTI折射介质的倾斜角。

表2 改进的Daley-Hron各向异性地层界面模型的参数
对于改进的Daley-Hron各向异性地层界面模型,由斯奈尔定律[21]可得
(6)
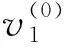
(7)
其中,
其中,
其中,
其中,
其中,
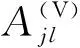
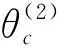
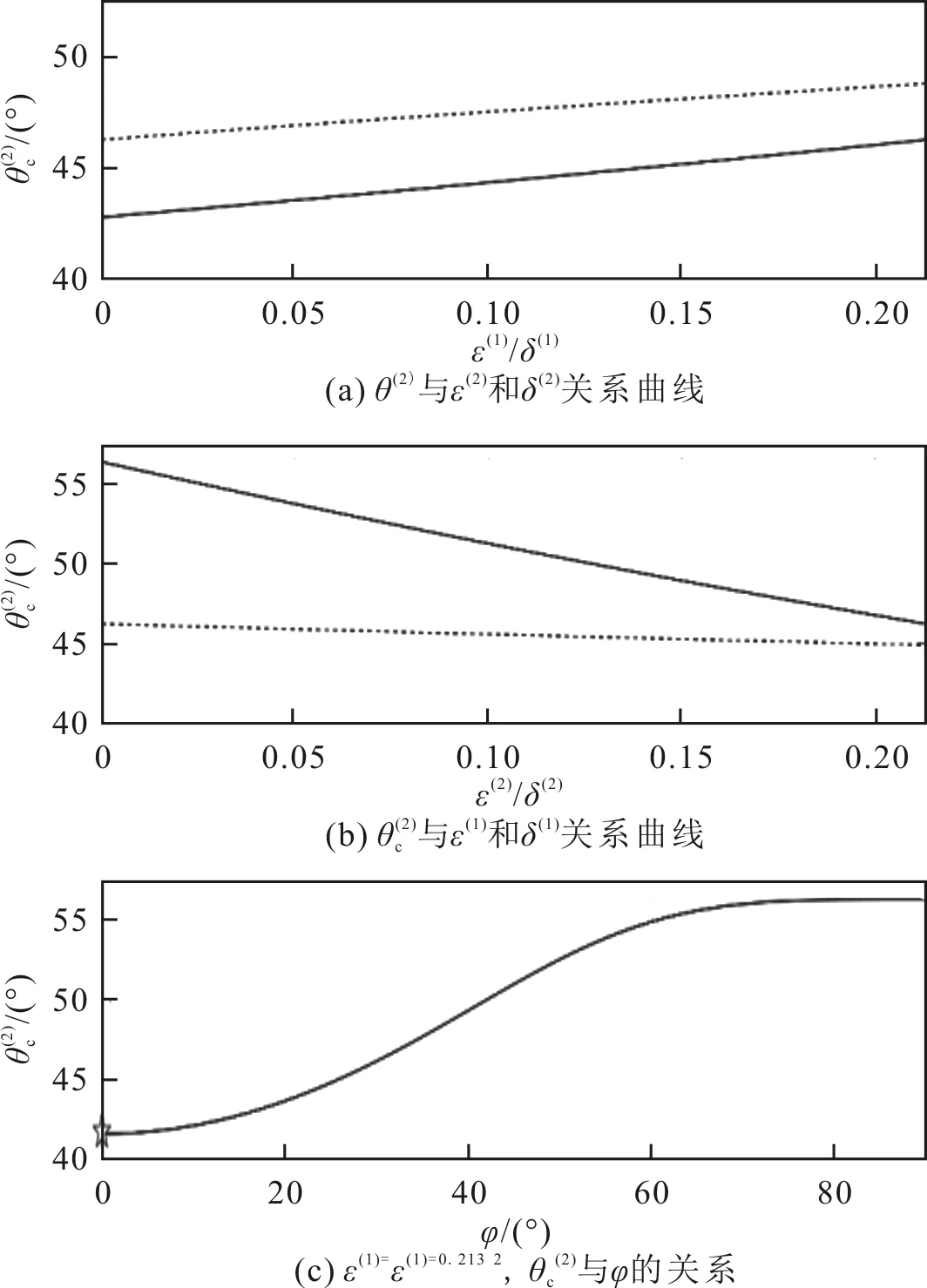
图3 各向异性参数和φ关系曲线的仿真结果
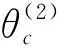
2.3 反射/折射、极化系数和质点位移
文献[17]中已经给出了VTI-TTI介质界面上产生的模式转换波极化系数的解析表达式和计算该界面反射/折射系数的矩阵方程。在VTI-TTI介质界面上,模式转换波的质点位移和极化态与反射/折射系数密切相关。
根据文献[17]中计算反射/折射系数和相位角的方法和表1中的参数,选择TTI介质的不同倾斜角,在φ分别为0°,30°,60°的条件下,仿真界面系统I和界面系统II的反射/折射系数R(m)、相位角φ(m)(m=1,2,3,4,分别表示反射P波、折射P波、反射SV波和折射SV波),仿真结果分别如图4和图5所示。

图4 不同φ,系统I中R(m)及φ(m)的仿真结果
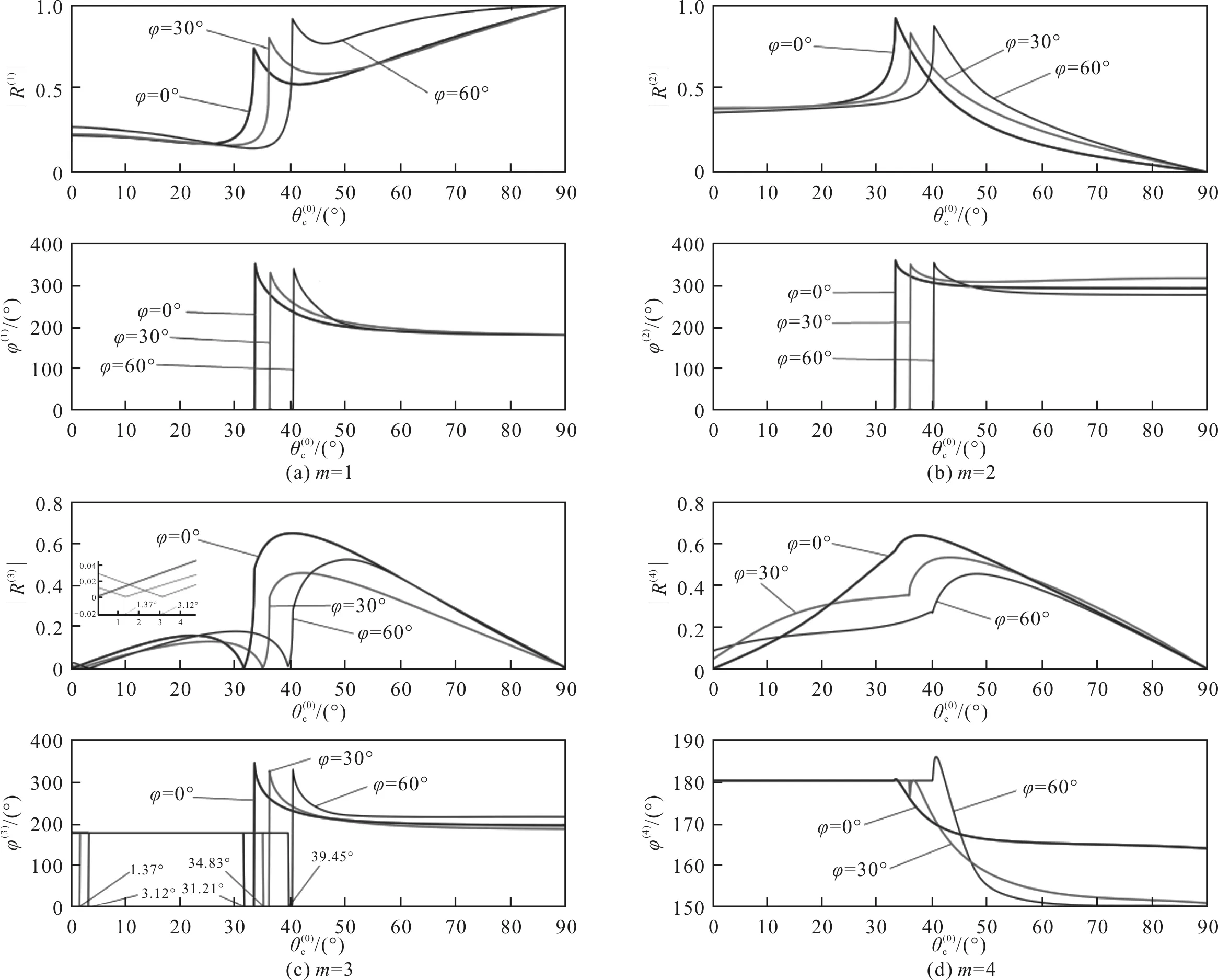
图5 不同φ,系统II中R(m)及φ(m)的仿真结果
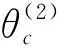
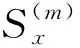

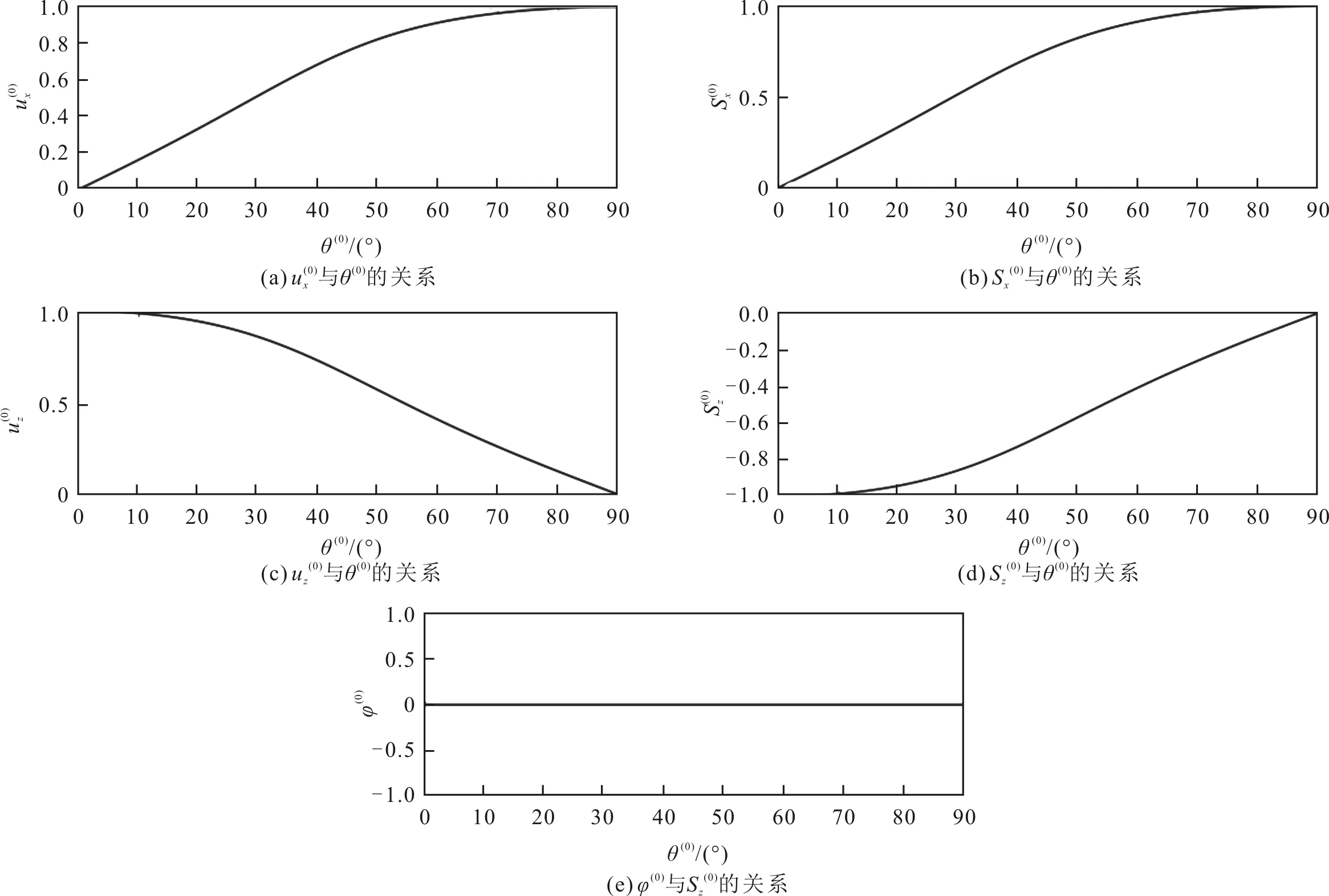
图6 入射波极化系数和位移矢量分量及相位角仿真结果
仿真界面系统I中的反射P波、折射P波、反射SV波和折射SV波等4种模式转换波的极化系数和位移矢量的分量及相位角与入射角θ(0)之间的关系,仿真结果分别如图7—图10所示。从图7(a)和图7(c)中,以及从图9(a)和图9(c)中可以看出,在TTI介质中,当倾斜角的φ分别为0°,30°和60°时,不同倾斜角下的反射P波和反射SV波的极化系数分量与入射角θ(0)之间的关系相同,关系曲线叠加在一起。

图7 系统I中反射P波极化系数和位移矢量的分量及相位角
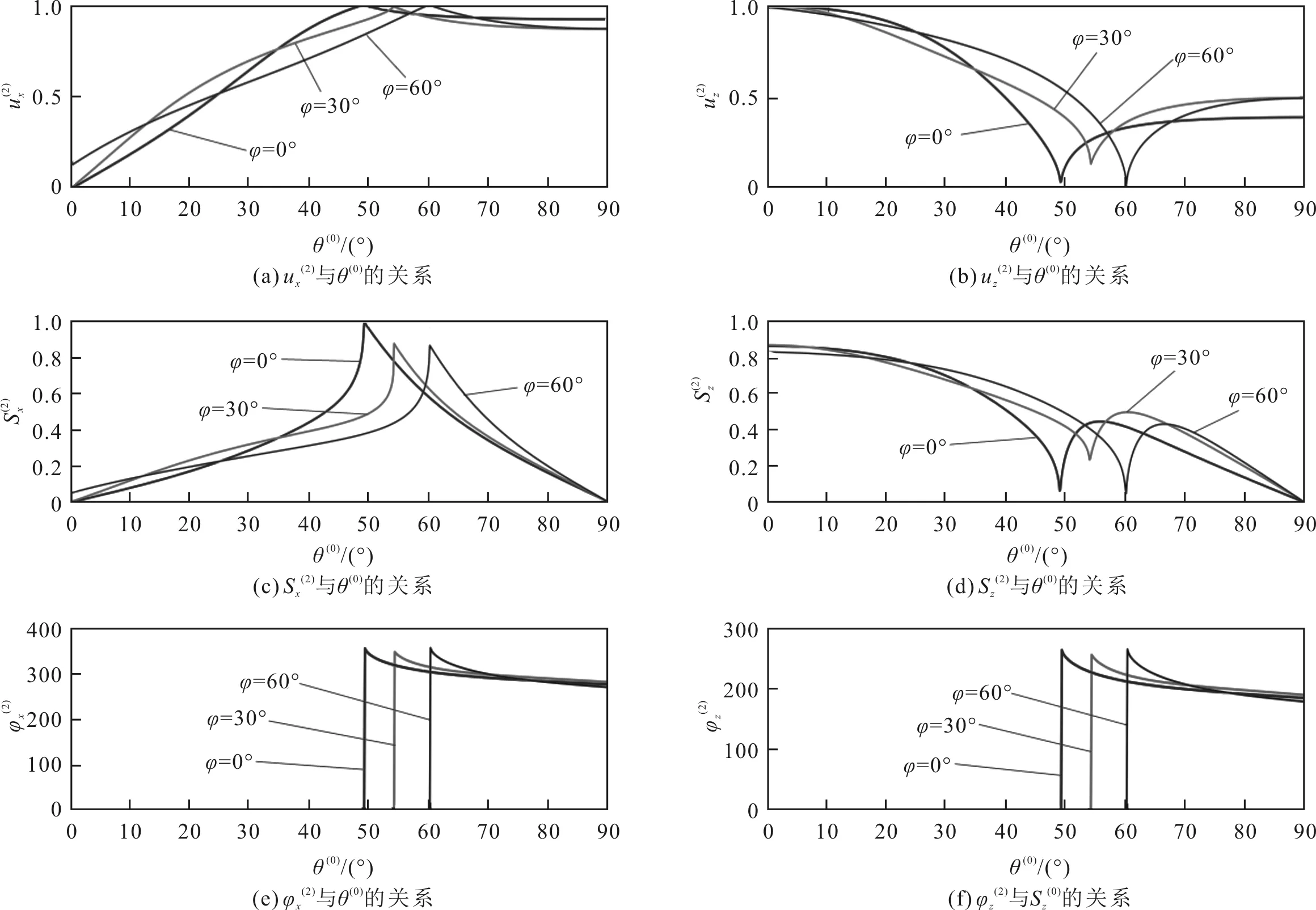
图8 系统I中折射P波极化系数和位移矢量的分量及相位角
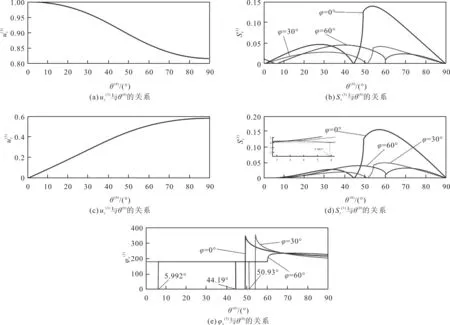
图9 系统I中反射SV波极化系数和位移矢量的分量及相位角
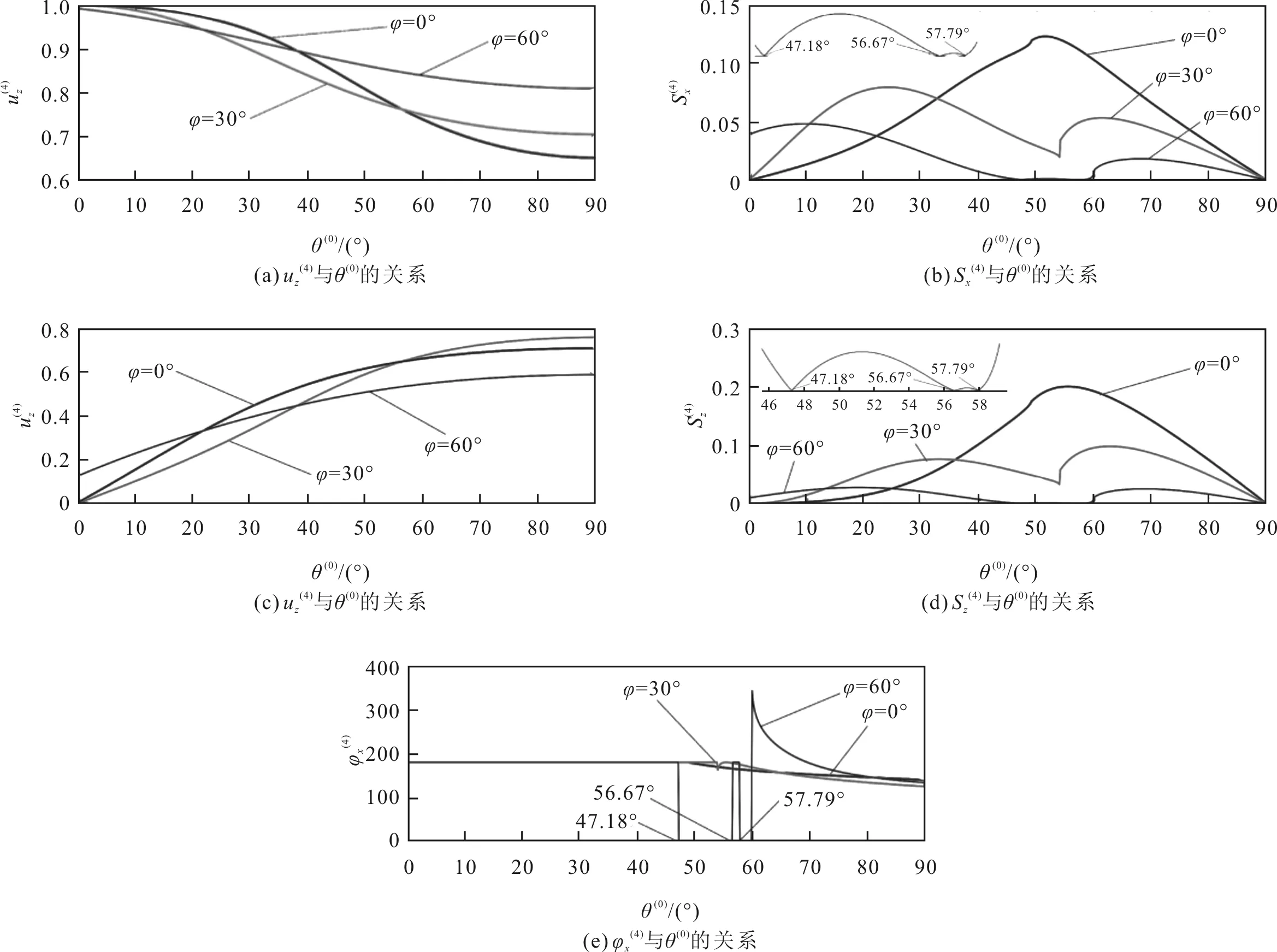
图10 系统I中折射SV波极化系数和位移矢量的分量及相位角
仿真界面系统II中的反射P波、折射P波、反射SV波和折射SV波等4种模式转换波极化系数和位移矢量的分量及相位角与入射角θ(0)之间的关系,仿真结果分别如图11—图14所示。从图11(a)和图11(c)中,以及从图13(a)和图13(c)中可以看出,当倾斜角的φ分别为0°,30°和60°时,不同倾斜角下反射P波和反射SV波的极化系数分量与入射角θ(0)之间的关系相同,关系曲线叠加在一起。

图11 系统II中反射P波极化系数和位移矢量的分量及相位角
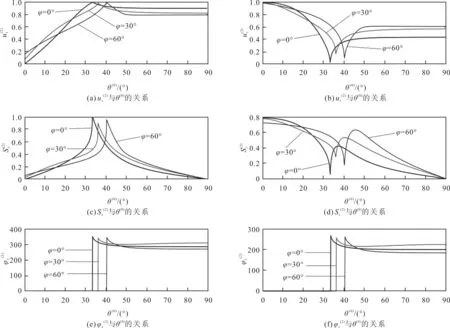
图12 系统II中折射P波极化系数和位移矢量的分量及相位角
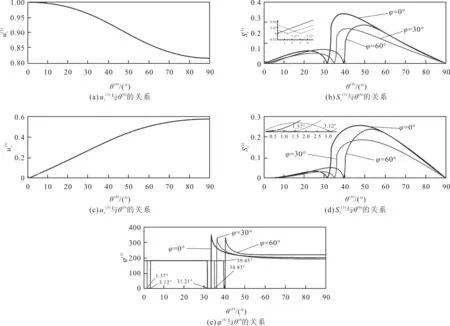
图13 系统II中反射SV波极化系数和位移矢量的分量及相位角
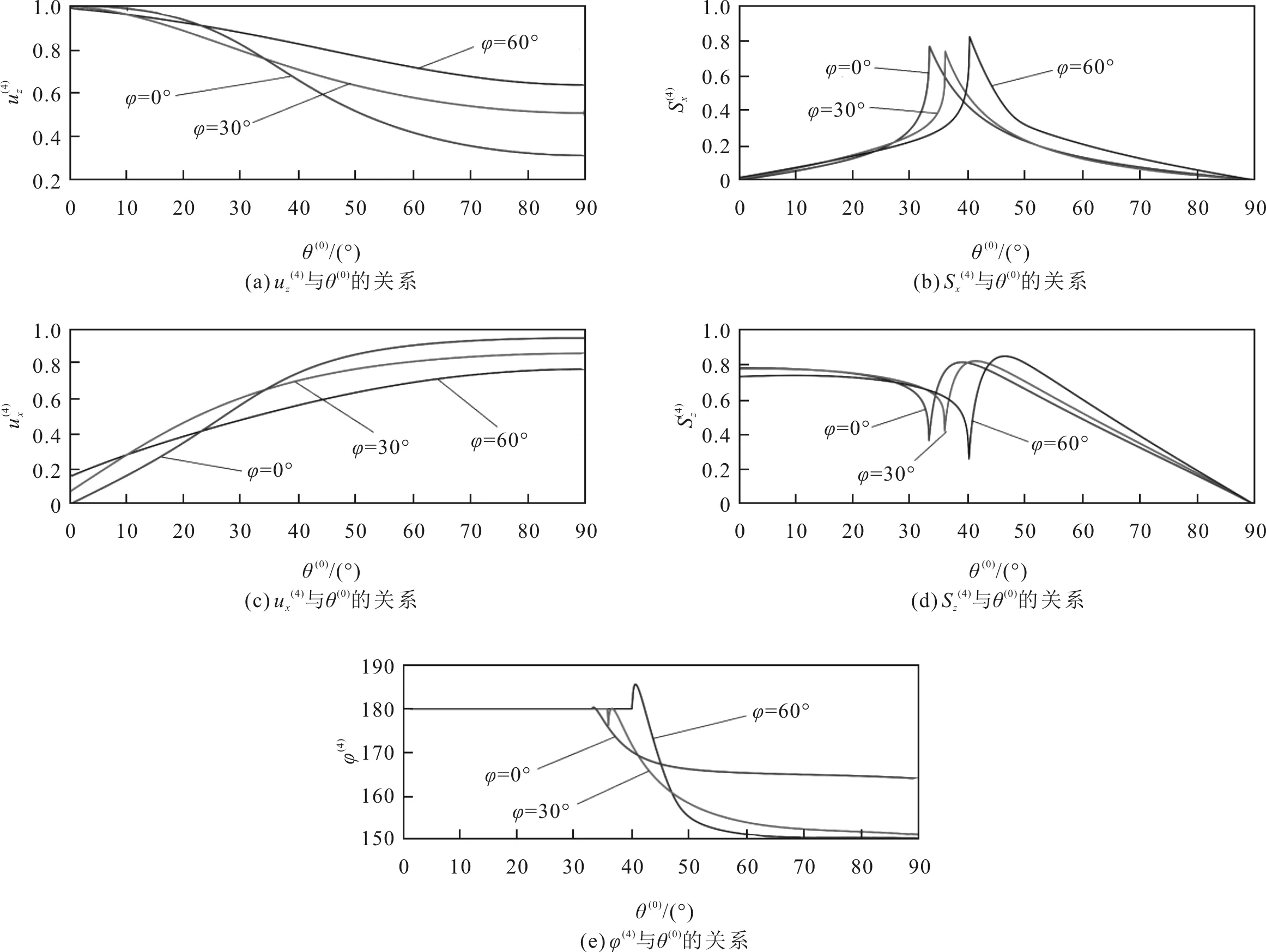
图14 系统II中折射SV波极化系数和位移矢量的分量及相位角
从图7—图14的仿真结果可知,TTI介质的倾斜角可能会影响VTI-TTI界面的特性(如反射系数),但是,不会改变反射P波和反射SV波在VTI介质中的传播特性。因此,对于各向异性页岩内的反射P波和反射SV波,其极化系数与倾斜角无关,如图7(a)和图7(c)、图9(a)和图9(c)、图11(a)和图11(c)、图13(a)和图13(c)所示。改变TTI介质的倾斜角不仅会改变VTI-TTI介质界面的折射特性(如折射系数),还会改变折射P波和折射SV波在TTI介质中的传播特性,因此,会影响折射P波和折射SV波的极化系数,如图8(a)和图8(b)、图10(a)和图10(c)、图12(a)和图12(b)、图14(a)和图14(c)所示。
从图8(e)和图8(f)以及图12(e)和图12(f)表明,对于界面系统I和界面系统II,在过第一临界角区域,非均匀折射P波的极化系数的x分量和z分量之间存在一个90°的相位差,即过第一临界角区域入射可以导致折射P波的极化系数的x分量和z分量之间产生90°的相移,从而使得折射P波从线极化波变成了椭圆极化波。
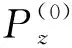
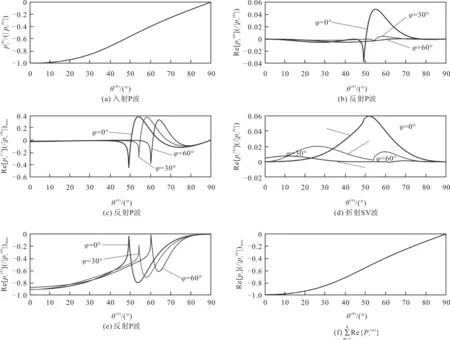
图15 系统I中功率流密度z分量的实数部分

图16 系统II中功率流密度z分量的实数部分
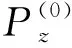
对计算出的极化系数以及反射和折射系数的正确性的另一种检查是,观察相关系数是否满足VTI-TTI岩石界面的边界条件。在入射VTI介质内存在入射P波S(0),反射P波S(1)和反射SV波S(3)等3种波。在折射TTI介质内存在折射P波S(2)和折射SV波S(3)两种波。
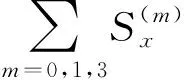

图17 系统I中的边界条件验证

图18 系统II中的边界条件验证

2.4 入射波/反射波/折射波的极化状态


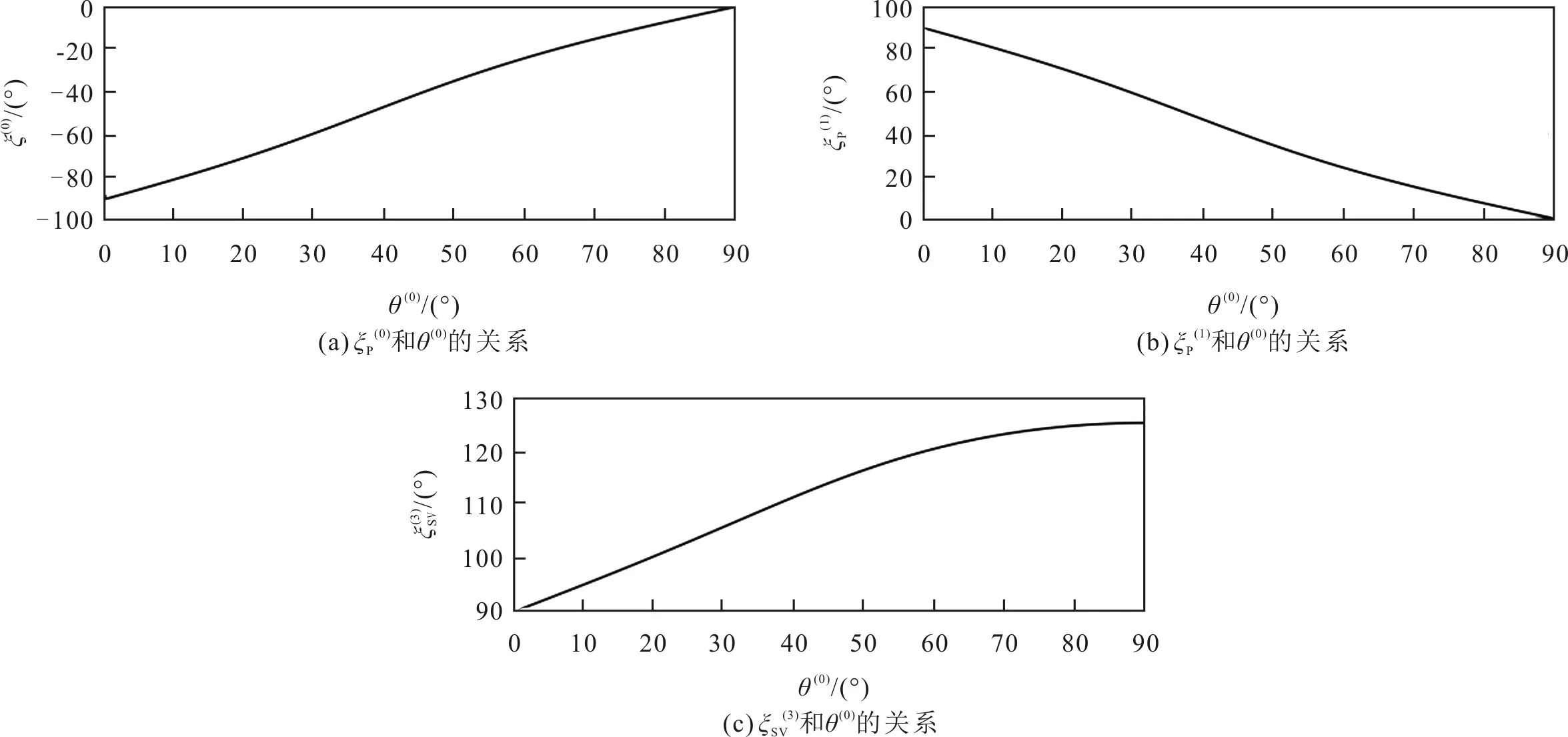
图19 系统I中和与θ(0)关系的仿真结果
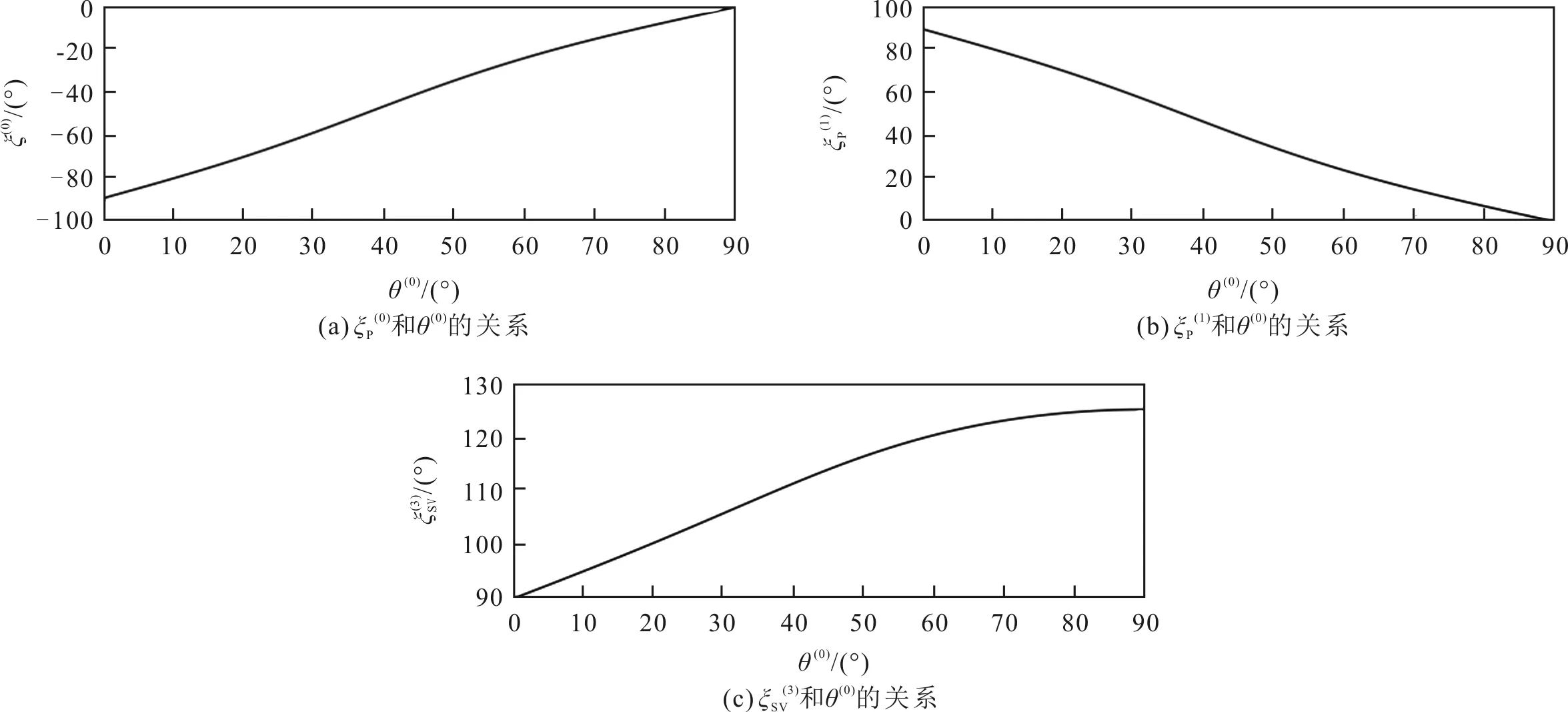
图20 系统II中和与θ(0)关系的仿真结果
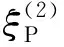

图21 系统I中和与θ(0)关系的仿真结果
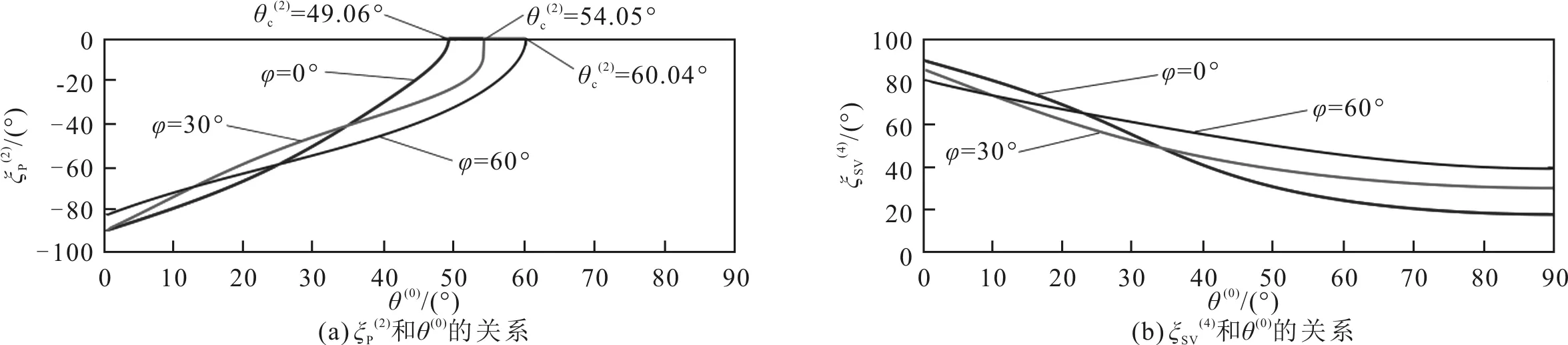
图22 系统II中和与θ(0)关系的仿真结果
图19—图22的仿真结果表明,TTI介质的倾斜角变化会改变线极化折射P波和线极化折射SV波的极化方向,但是,对线极化反射P波和线极化反射SV波的极化角没有影响。这个物理现象的原因可能是,TTI介质的倾斜角是折射TTI介质本身的物理特性,其只会影响在TTI介质中的折射P波和折射SV波的特性,而不会影响在VTI入射介质中反射P波和反射SV波的特性。

图23 系统I中椭圆极化波随入射角变化的仿真结果

图24 系统II中椭圆极化轨迹随入射角变化的仿真结果
从图23和图24的仿真结果可以看出,VTI-TTI界面系统的物理参数和各向异性参数,对于非均匀折射P波的物理特性和椭圆极化波轨迹特征有着重要的影响。另外,椭圆极化波轨迹还随着TTI介质倾斜角的变化而变化。与TTI介质倾斜角的作用相比较,入射角对椭圆偏振轨迹有更大的影响,TTI介质倾斜角和入射角不仅影响椭圆偏振波轨迹的大小,而且还影响它的形状。
3 结论
以各向异性页岩-泰勒砂岩界面和各向异性页岩-油质页岩界面构成了两种VTI-TTI各向异性介质界面系统,并且得到了与P波为入射角相对应的4种模式转换波。使用MATLAB对文献[17]推导出的求解相速度的解析表达式和极化系数解析表达式进行数据仿真,得到如下结论。
1) 以改进后的Daley-Hron各向异性介质为界面系统,仿真出的慢度曲线解释了VTI-TTI介质界面系统似乎有一个对应折射SV波的第二临界角,而在实际中却没有的物理现象。界面系统的入射临界角是否存在,由界面两侧介质本身的物理特性(物理参数和各向异性参数)和几何结构(TTI介质的倾斜角)决定。
2) 在无限大的TTI介质中,P波和SV波的慢度曲线关于垂直轴不对称,而在VTI-TTI介质界面上产生的折射P波和SV波的慢度曲线作为入射角的函数关于垂直轴对称。
3) 第一临界角与入射角无关,其完全由入射/折射介质的各向异性参数和折射介质的倾斜角所决定,各向异性参数和TTI折射介质的倾斜角的值越大,入射临界角就越大。
4) 对于各向异性页岩内的反射P波和反射SV波,其极化系数与倾斜角无关,但不同的倾斜角会影响折射P波和折射SV波的极化系数。并且,依据能量守恒和声学边界条件,对计算出的反射系数、折射系数、极化系数和质点位移进行了双重验证。
5) TTI介质的倾斜角和入射角对椭圆偏振波轨迹和其形状都有影响,与TTI介质倾斜角的作用相比较,入射角对椭圆偏振轨迹的影响更大。

