一种抗几何攻击的多重零水印算法

梁 猛，王春洋，杨敏璇

(西安邮电大学 电子工程学院， 陕西 西安 710121)

随着网络和数字多媒体的快速发展，大量的数字化产品如视频、音频和数字图像等在网络上飞速流传。利用互联网传输与交换的医学影像、军事卫星图像等以图片为载体的信息更为简洁明了，得到了广泛的应用，同时，也带来了信息安全问题。针对图像信息在互联网传播的信息安全问题，人们提出了各种保密技术。其中，数字水印[1]是一种被广泛采用的保密技术，该技术事先将有意义的信息嵌入到数字产品中，以实现信息加密并利用互联网传播加密信息。当接收方接收到经过加密的信息后，通过嵌入方法的逆向操作将事先嵌入的信息提取出来，进行解密，获取加密前的原始信息。

经典的数字水印技术无法同时兼顾水印不可见性与鲁棒性之间的矛盾[2]，零水印技术的出现很好地改善了这个问题。零水印技术利用载体内部重要不变特征，如纹理、边界和其他一些内部元素等构成的特征矩阵，与水印信息进行某种运算构成零水印对数字图像进行加密，并将零水印保存在第三方。在出现信息安全问题时，通过相同运算与保存在第三方的零水印进行比对，如果相似度在相应的阈值内，则认为存在水印，否则不存在。零水印技术不再将水印信息嵌入到载体内部，因此无需平衡不可见性与鲁棒性之间的矛盾。

目前已提出的零水印算法有很多[3-9]，例如，文献[7]利用天牛须优化算法改善零水印算法中的虚警率问题和对角线失真问题，文献[8]利用Slant和LU分解法提升了不可见性和运算速度，但是，这两种算法的鲁棒性较差。文献[9]提出一种基于低频奇异值均值的零水印算法，该算法具有较强的鲁棒性，所得到的归一化互相关函数值可达到0.98，部分可达到1.00，鲁棒性较好，但和其他的零水印算法一样，都只实现了单一的水印嵌入，并且水印的容量有限。

与网络保密技术相对应，针对各种网络保密技术的网络攻击技术也在迅速发展。图像数字水印通常会受到两种类型的攻击[10]：一种为常规信号处理攻击，包括滤波、压缩以及噪声攻击等；另一种为几何攻击，包括旋转、缩放、长宽比改变以及剪切等攻击方式。数字水印技术在面对几何攻击时，由于载体位置发生了相对变化，导致数字水印嵌入与提取不再同步，水印的提取效果大幅下降[11]。几何攻击是一种全局性的攻击方式，对水印提取影响远大于常规信号处理攻击。研究抗几何攻击的水印算法具有重要的意义。

基于此，本文拟提出一种抗几何攻击的多重零水印算法，应用变换矩阵和Hu矩生成特征矩阵，再与水印图像异或生成零水印。在实现多个水印嵌入的同时，提升算法的抗几何攻击性能。

1 预备知识

1.1 SURF检测特征点

快速鲁棒特征[12](Speeded-Up Robust Features,SURF)算法是对尺度不变特征变换[13](Scale Invariant Feature Transform,SIFT)算法的一种改进。SURF算法舍弃了SIFT利用不同尺寸的图像与高斯函数进行卷积的操作，改用积分图像、Harr小波变换、和近似Hessian矩阵[14]降低计算复杂度，以提高算法的效率。Hessian矩阵是SURF特征点提取的核心，给定图像I中的一个点(x,y)，在尺度空间理论中，在该像素点处，二阶高斯滤波尺度条件下的Hessian矩阵定义[14]为

(1)

式中：x，y表示图像的像素坐标；Lxy、Lyy和Lxy分别为高斯滤波二阶微分算子在该像素点处与原图像的卷积[14]。

可以求得矩阵Hxy的判别式[14]为

(2)

1.2 变换矩阵

平面的几何变换[15]可以理解为一幅图像内的特征点与另外一幅图像的特征点进行特征匹配后，将匹配的特征点坐标代入到一个3×3的变换矩阵中，利用两幅图像的特征点坐标之间的对应关系解出矩阵内的各个参数。利用变换矩阵能够将一幅图像变换成另一幅图像，其大小、形状均与原图像相同。

假设一幅图像和另外一幅图像对应点的对齐次坐标分别为(x′,y′,1)，(x,y,1)，则有[16]

(3)

式中，H为变换矩阵。

将式(3)展开并整理得到

(4)

(5)

可以将式(4)和式(5)表示为矩阵形式[16]，即

(6)

其中，

h=(h11,h12,h13,h21,h22,h23,h31,h32,h33)

(7)

a11=(x,y,1,0,0,0,-xx′,-x′y,-x′)

(8)

a12=(0,0,0,x,y,1,-xy′,-yy′,-y′)

(9)

令

A=(a11,a12,…,aN1,aN2)T

(10)

式中，N为特征点对个数。

则可以得到方程[16]

AhT=0

(11)

采用齐次坐标，对图像进行旋转、缩放、平移和透视投影等线性操作。在采用齐次坐标条件下，对矩阵H中的参数进行求解，令矩阵H的模为1，则有

(12)

根据式(12)可知，h33可以由变换矩阵内其他元素表示。一对特征点对可以得出两个方程，所以至少需要4组点对才能够计算出变换矩阵内所有参数。

当原图像特征点与受到几何攻击的水印图像特征点一一对应产生的特征点对的个数为N时，可以得到线性方程组[16]

(13)

1.3 Hu矩

Hu矩是由中心矩推导出的7个矩不变量，这7个矩不变量对旋转、平移、缩放都有着很强的鲁棒性[17]，因此，Hu矩被广泛的应用到目标识别、图像分析等领域[18]。然而，后续的研究发现，如果只依靠这7个不变矩来进行目标识别或是应用到其他复杂的场景中时，往往无法同时分辨出较为复杂的多幅图像，不能达到令人满意的效果[19]。文献[19]利用三角函数生成法建立了一种不变矩空间，推导出了5个新的不变矩。扩展后的不变矩在复杂的目标识别中可以达到较好的效果。

设一幅离散的数字图像f(x,y)，其长、宽分别为m和n像素，则图像f(x,y)的p+q阶矩定义为[17]

(14)

式中，p,q=0,1,2,…。

f(x,y)的p+q阶中心矩的定义为[17]

(15)

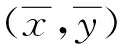
研究发现，f(x,y)的中心矩经归一化后具有尺度不变性[17]。归一化后的中心矩定义为[17]

(16)

其中，

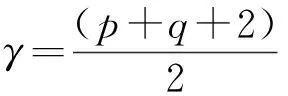
2 算法实现

2.1 水印图像Arnold置乱

使用Arnold变换通过改变图像像素灰度的分布达到隐藏信息的目的[20]。一幅L×L像素大小的数字图像的二维Arnold变换的定义为[20]

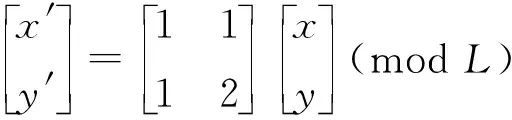
(17)

式中：(x,y)为原图像像素点坐标；(x′,y′)为置乱后像素点坐标。

Arnold置乱后，得到加密图像，并保存密匙K。

2.2 零水印的构建

假设原始载体图像为I，置乱后的水印图像分别为W1，W2，…，零水印的构造流程如图1所示。

图1 零水印的构造流程图

零水印构造流程主要有如下步骤。

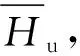
步骤2检测原始载体图像的SURF特征点。根据文献[21]可知，当特征点选取在图像内接正方形安全区域内时，不会受到因旋转带来的像素丢失。此时，控制选取特征点的个数N(N≥4)，在保证无交叉线条件下，将选取的特征点逐个连接，得到一个N边形。确定该N边形后，计算出该N边型与原始载体图像最大内接正N边型的变换矩阵HN。对该变换矩阵进行与步骤一相同的二值化操作，得到二值化后的变换矩阵HN,2。

步骤3对矩阵Hu,2与HN,2(N=4,5,…)分别进行异或操作，得到的二值矩阵作为特征矩阵H2,N。将得到的特征矩阵分别与加密水印进行异或操作，得到多个版权信息零水印以及相应的时间戳，送至第三方权威机构认证中心进行注册。

2.3 零水印的提取

1)首先对载体图像可能受到的几何攻击进行检测并校正。

定义参数ω，用于衡量待测图像与原图像差距[19]。若ω大于等于设定的阈值，则认为不含水印；否则，认为存在水印。确认水印存在的情况下，通过选取不同个数的特征点计算出不同的变换矩阵并分别与原始载体图像的Hu二值矩阵进行异或运算，构成新的特征矩阵。

4)从第三方获取零水印信息与得到的多个新的特征矩阵进行异或操作，根据密匙K进行Arnold逆变换，得到嵌入在同一幅载体图像的多幅水印图像。

3 仿真结果及分析

3.1 实验环境及参数

采用Matlab验证所提算法的有效性，并与基于低频奇异值均值的强鲁棒零水印算法[9]进行对比。另外，为了验证所提算法的鲁棒性，在试验过程中采用归一化相关(Normalization Cross Correlation,NCC)系数[10]客观评价提取水印与原水印之间的相似程度。

选取Lake、Lena和Baboon等3幅经典灰度图像作为为载体图像，3幅灰度图像的大小均为512×512像素，选择的载体图像如图2所示。采用水印1“吉林长春”和水印2“陕西西安”两幅二值图像作为水印图像，水印图像均为40×40像素大小，选择的水印图像如图3所示。对Lake、Lena和Baboon等3幅载体图像进行顺时针旋转15°攻击，顺时针旋转15°攻击校正后的实验结果图4所示。从图4中可以看出，选取的3幅图像在遭受顺时针旋转15°攻击后，均能很好地提取出水印。

图2 载体图像

图3 水印图像

图4 顺时针旋转15°攻击校正后的实验结果

下面以载体图像Lena为例，对Lena图像进行顺时针旋转4°攻击和镜像攻击，其Hui值实验结果如图5所示。选取与Lena图像相似的人物图woman A和woman B，计算Lena图像、woman A图像和woman B图像3幅图像的Hui值，实验结果如图6所示。从图5可以看出，对Lena图像进行顺时针旋转4°攻击和镜像攻击得到的Hui值保持稳定，几乎不变。而从图6可以看出，相似但不同图像的Hui值相差较大。说明对于同一幅图像经过不同几何攻击之后Hui值具有很好的稳定性，而不同的图像Hui值具有较大的差别。因此，采用Hui值来构建特征矩阵不单可以抵抗几何攻击，还可以在一定程度上降低水印检测的虚警率。

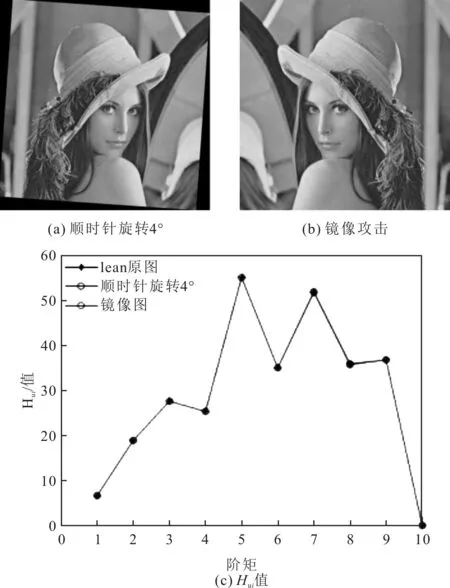
图5 不同攻击方式图像Lena的Hui值实验结果

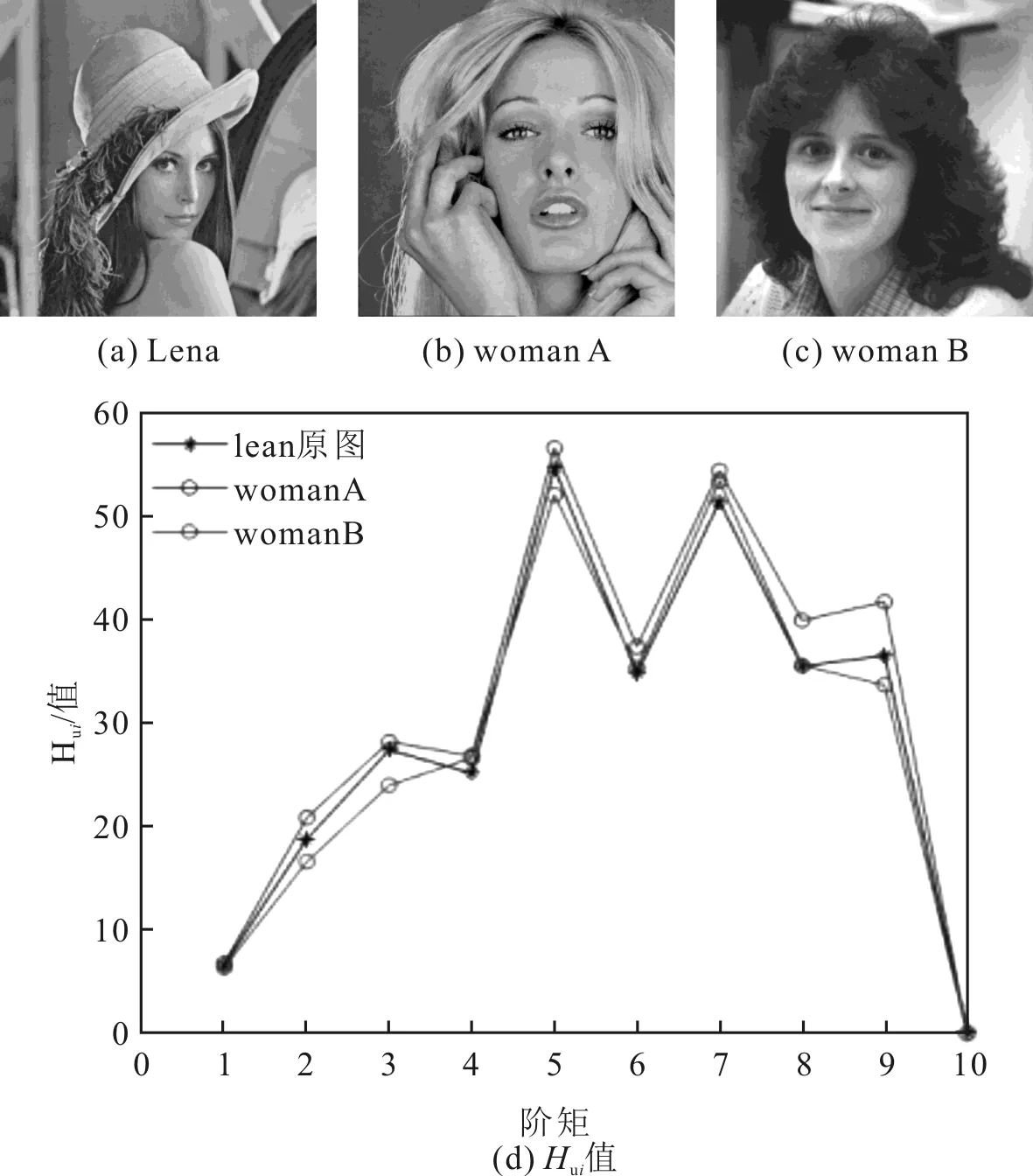
图6 不同相似图像的Hui值

3.2 几何攻击

采用的几何攻击主要方式是对图像进行了旋转、缩放以及剪切攻击。对受到几何攻击的待测载体图像利用变换矩阵进行几何校正。

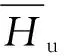
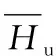
表1 不同旋转角度攻击校正后Hui值及

表2 不同旋转角度攻击校正后的Hu,2

从表1和表2可以看出，当遭受到不同的旋转攻击时，虽然Hui值及其均值有略微变化，但是，变化幅度较小，且对二值化后的Hu矩阵没有产生影响，Hu,2保持不变。

不同旋转角度攻击校正后的特征点坐标如表3所示，可以看出，不同旋转角度攻击校正后载体图像特征点坐标变化较小，取整后保持稳定，未发生变化。说明所提方法抵抗旋转攻击性能较好。

下面以Lena、Lake和Baboon图像为例，分别进行不同的几何攻击测试。旋转攻击的方式为，以载体图像中心点为旋转中心进行1°、5°、15°、30°、75°和145°的顺时针旋转操作；缩放攻击方式为先缩小0.5倍再放大2倍以及先缩小0.25倍再放大4倍操作；剪切攻击方式为剪切左上角1/4和右上角1/4操作。

攻击校正后提取水印NCC值如表4所示，可以看到，算法对旋转和缩放攻击鲁棒性较好，所得到的归一化互相关函数值均可达到1.000，但面对剪切攻击时，算法无效。这是因为，经过剪切攻击后无法判断剩余部分嵌入水印信息的位置，从而导致无法提取正确的水印。

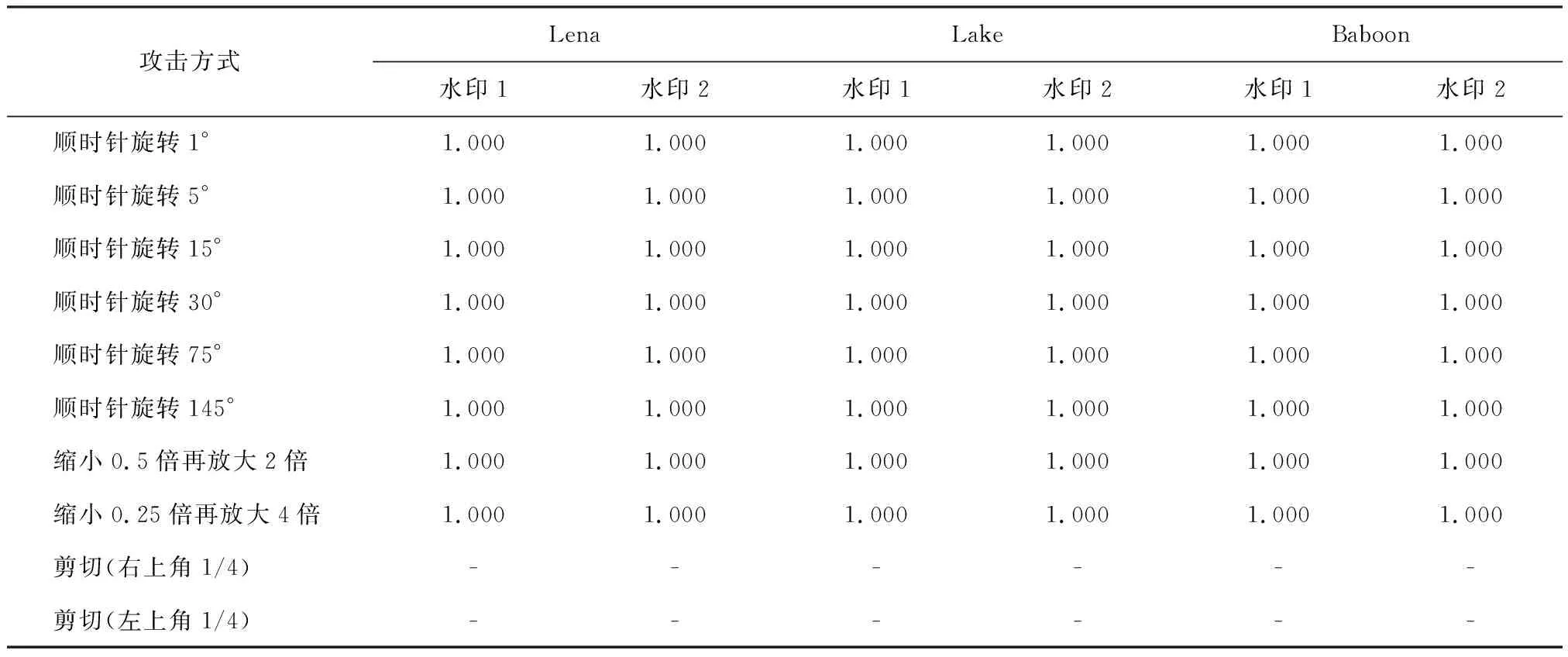
表4 攻击校正后提取水印NCC值

3.3 JPEG压缩攻击

以Lena、Lake和Baboon图像为例，分别进行联合图片专家组(Joint Photographic Experts Group,JPEG)压缩攻击测试，不同压缩强度攻击下提取水印NCC值实验结果如表5所示。可以看出，所提算法对JPEG压缩攻击有着较强的鲁棒性。

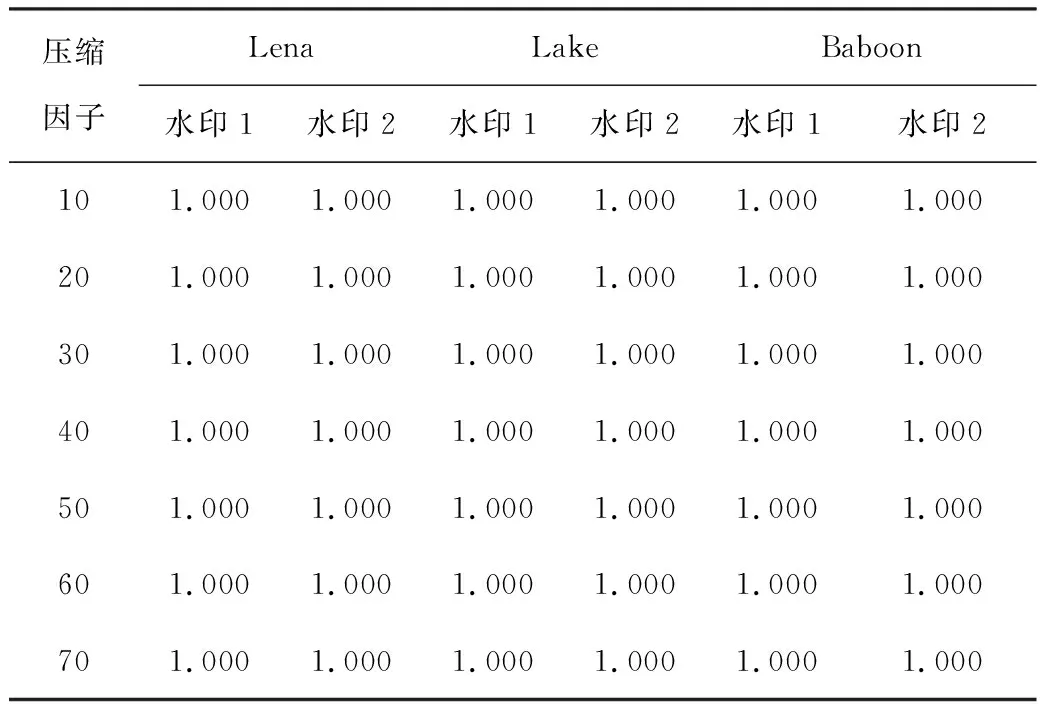
表5 不同压缩强度攻击下提取水印NCC值

3.4 其他方式攻击

以Lena、Lake和Baboon图像为例，分别进行方差为0.01的高斯噪声、密度为0.01的椒盐噪声和滤波模板为3×3的中值滤波攻击测试，不同攻击方式下提取水印NCC值实验结果如表6所示。可以看出，所提算法对噪声攻击有着较强的鲁棒性。

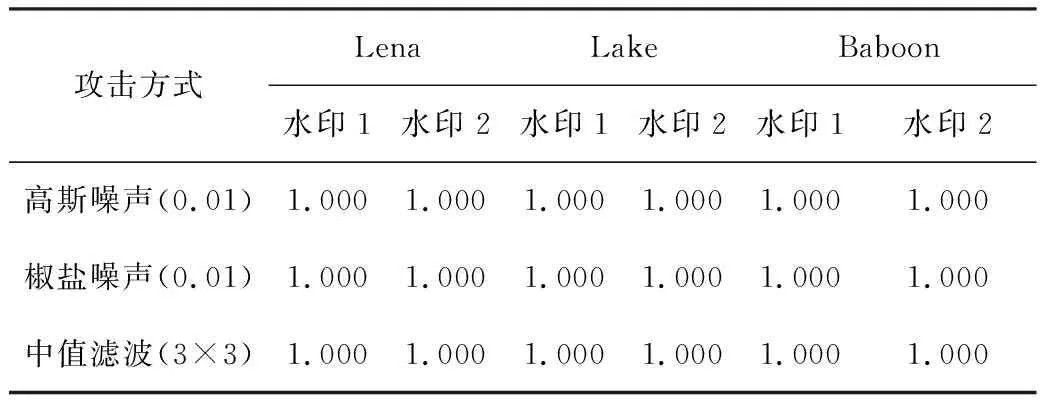
表6 其他攻击方式下提取水印NCC值

3.5 对比实验

为了进一步验证所提算法的性能，选择与基于低频奇异值均值的强鲁棒零水印算法[9]相同的Lake载体图像进行实验，所提算法与文献[9]算法的NCC值分别如表7所示。可以看出，所提算法和文献[9]对高斯噪声的抵抗能力相同，但是，对于椒盐噪声、滤波攻击和旋转攻击抵抗能力均高于文献[9]算法。

表7 所提算法与文献[9]算法的NCC值

经过实验，得到如下结论。

1)所提算法具有较强鲁棒性。这是因为，一方面，载体图像在经过传统的压缩攻击、噪声攻击或是几何攻击后，由于图像SURF特征点始终保持稳定，使得记录由不同个数的特征点所构成的不同N边型与正N边型之间的对应关系的二值化变换矩阵始终保持不变，通过变换变换校正操作后，载体图像已经较为接近原图像。另一方面，对于同一幅图像计算所得到的Hu矩的稳定性较好，矩值波动只在很小范围内，导致二值化后的Hu矩阵始终不变。由于零水印构建所需特征矩阵是由二值化后的变换矩阵和Hu矩阵经过异或运算所得，因此，算法具有较强的鲁棒性。

2)所提算法具有较好安全性。这是由于，特征矩阵是由二值变换矩阵和二值Hu矩阵异或所得，算法在进行特征点检测时，可以通过控制特征点的个数来控制特征匹配后生成的相应变换矩阵。只有当收信一方知晓所选特征点个数以及如何得到变换矩阵时，才可以提取水印。这在一定程度上提高了算法的安全性。

3)所提算法能够实现多水印的嵌入。这是因为，通过控制特征点个数得到多个不同的多边形，由这些多边形与载体图像最大内接正多边形特征匹配后可以得到多个不同的变换矩阵，以此获得多个特征矩阵，从而实现了多幅水印图像的嵌入。

4 结语

提出一种可以同时嵌入多幅水印图像并具有较强鲁棒性的零水印算法。首先，对载体图像进行SURF特征点检测，得到具有较强稳定性的特征点。其次，分别根据这些不同个数的特征点依次无交叉连接得到的多边形与载体图像最大内接正多边形进行特征匹配得到相对应的变换矩阵。最后，对载体图像进行计算得到Hu矩，将二值化后的多个变换矩阵分别与载体图像二值化Hu矩进行异或，得到多个不同的零水印信息。在构造零水印的过程中，利用Arnold置乱提高水印安全性，并在提取水印前利用变换矩阵校正载体图像，提高了算法鲁棒性。所提算法对于旋转、缩放、JPEG压缩等攻击基本可以达到100%的水印提取效果，且实现了多幅水印图像的嵌入。

但是，所提算法在选取特征点个数过多时，可能会出现多点共线问题，导致水印容量下降，以及面对较大面积剪切时出现算法失效的问题，有待进一步研究。