无人机边缘计算高能效任务完成率最大化方案

刘伯阳，王怡心，杨宁乐，党儒鸽，万奕尧

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

信息与通信技术(Information and Communications Technology，ICT)的快速发展激发越来越多对复杂度与时延要求高的新应用与新业务，如增强现实(Augmented Reality，AR)、虚拟现实(Virtual Reality，VR)及超清直播等。然而，目前大部分移动终端受限于其成本、尺寸、算力以及有限的电池电量，难以长期稳定运行上述业务，部分低成本设备甚至无法独立运行。为缓解此类问题，移动边缘计算(Mobile Edge Computing，MEC)技术被提出[1-2]。在MEC网络中，MEC服务器部署于网络基站处，为地面用户提供计算服务。考虑服务器部署位置固定，网络中与基站之间无线链路遮挡严重的用户不能获得高质量计算服务。另外，网络中固有的MEC服务器计算能力在满足一些大型赛事、演唱会及集会等突发计算任务密集产生场景的要求时易出现问题。因此，需要一种更为灵活的MEC网络服务架构。

无人机(Unmanned Aerial Vehicle，UAV)具有高机动性与灵活性，易避开建筑物等遮挡与地面用户建立高质量视距链路，且可随时部署于突发的密集计算任务产生区域[3]。因此，MEC与UAV的结合得到广泛关注。文献[3]对用户的CPU频率、任务卸载时间长度以及UAV发送功率与飞行轨迹进行联合优化，最大化UAV-MEC网络计算速率。文献[4]对计算任务分配比例、上下行通信资源调度参数以及UAV飞行轨迹进行优化设计以最小化网络能耗。还有关于UAV-MEC网络中地面用户能耗最小化问题的研究，对UAV部署位置、工作时隙分配以及任务分割比例进行优化设计[5]；通过优化UAV三维空间轨迹、用户通信带宽以及UAV发送功率最大化计算效率[6]；利用多智能体深度强化学习算法对UAV轨迹等参数进行设计，对用户部署公平性、UAV之间的负载公平性以及用户整体能耗进行优化[7]；通过一种认知UAV-MEC网络架构，将认知技术引入UAV-MEC网络中，在提升网络频谱效率的同时最小化网络能耗[8]。文献[9-10]将UAV作为移动中继，利用UAV在地面用户和远端基站之间搭建起高质量视距信道，在任务高发阶段，UAV可以将无法及时处理的任务进一步卸载到远端基站进行处理。以地面用户服务时延以及UAV的飞行能耗加权和最小化为目标，联合优化UAV的飞行轨迹、计算资源分配以及任务卸载决策，降低了物联网系统中传感器时延，并提升了UAV的续航时间[11]。为了进一步降低地面终端的任务时延，文献[12]将UAV作为空中基站收集地面传感器的信息，以全部地面终端时延之和最小化为目标，联合优化了UAV的飞行轨迹和资源调度。同时，文献[13]考虑了基于多UAV协同的MEC网络，联合优化了各UAV飞行轨迹及用户调度，实现了用户吞吐量最大化。上述研究均基于相同的假设，即UAV可以完成全部地面用户的计算需求。但是，UAV搭载与续航能力有限，其可搭载的服务器性能有限，在地面用户计算任务量较大或用户数量较多时，UAV很难独立完成地面用户全部的计算任务。

针对UAV算力与能量有限情况下的MEC网络服务覆盖范围不足问题，拟提出一种UAV算力、UAV轨迹、用户卸载任务量与UAV卸载任务量的联合优化方案。该方案利用分块迭代、拉格朗日对偶以及连续凸近似(Successive Convex Approximation,SCA)算法对所建立的数学优化问题进行求解，并优化设计网络参数。通过在不同网络参数下对所提方案性能进行仿真与分析，验证所提方案的有效性，以期实现在最小化UAV-MEC网络能耗的同时最大化地面用户任务完成率。

1 系统模型

所提方案是由一个地面基站、一个UAV与K个地面用户构成的UAV-MEC网络架构，具体的系统模型如图1所示。

图1 系统模型

令集合QK={1,2,…,K}表示地面用户集合，地面基站与UAV均搭载了移动边缘计算服务器。假设地面用户与基站之间由于遮挡等原因不存在直接链路，如果地面用户计算能力弱，则其无法单独进行任务计算。为此，可将待计算任务上传至UAV，UAV再通过本地计算与将待计算任务转发至地面基站进行用户任务计算。

1.1 坐标与信道模型

考虑笛卡尔三维坐标系、基站与地面用户高度为0 m，基站水平坐标为wb=(xb,yb)，第k个地面用户水平坐标为wk=(xk,yk)，UAV飞行高度设置为H，此高度为避开障碍物并与地面基站用户建立直接链路的最低安全高度。UAV从起始水平位置qI飞往终点位置qF，最大飞行时延为Δs。为了方便分析与优化系统参数，将总时延均分为N个时隙，每个时隙长度表示为T=Δ/N，令QN={1,2,…,N}表示时隙集合，令q[n]表示UAV第n个时隙的水平坐标。

由于UAV与基站以及地面用户有直接链路的场景，第n个时隙UAV与基站以及第k个地面用户之间的信道功率增益分别建模为[3]

(1)

(2)

式中：βk(k=0,1,…,K)表示参考距离为1 m时的信道功率增益；∀k∈QK,∀n∈QN。

1.2 计算与能耗模型

每个地面用户均具有待计算任务。用二元组(Lk,Ck)描述第k个地面用户的任务，其中Lk表示待计算任务量，Ck表示计算1 bit任务需要耗费的CPU周期数。地面用户通过频分多址(Frequency Division Multiple Access,FDMA)的方式将任务上传至UAV处，上传带宽为BU。令lk[n]表示第k个地面用户在第n个时隙上传给UAV的计算比特数，则其第n个时隙上传能耗为

(3)

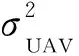
令fk[n]表示UAV在第n个时隙分配给第k个地面用户的算力，则UAV在第n个时隙的计算能耗为

(4)

式中，γ为能耗因子。

采用文献[14]中的模型，UAV飞行功率为

(5)

其中，

式中：v[n]为速度矢量；P0与PH分别与无人机螺旋桨旋翼功率与诱导功率有关的常数；Utip表示无人机旋翼尖端的转速；v0为无人机悬停时的平均旋翼诱导速度；ρ0、A、d0和s分别表示空气密度、无人机旋翼面积、无人机机身阻力比以及旋翼实度[14]。

UAV将部分任务在本地计算后，采用时分多址(Time Division Multiple Access，TDMA)的方式将其余任务卸载至基站进行计算。每个用户的任务在其对应的子时隙内进行卸载，子时隙长度为δ=T/K。令rk[n]表示UAV在第n个时隙卸载的第k个地面用户的任务量，则UAV在第n个时隙总能耗为

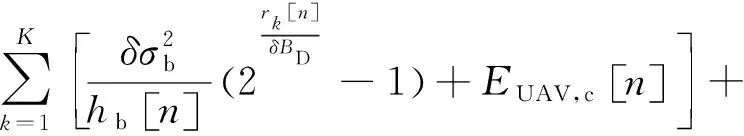
(6)

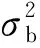
1.3 问题建立

为最大化用户任务计算率、用户能耗与UAV能耗加权和，优化问题建立如下。

(7)

C4:fk[1]=0,rk[1]=0

C5:lk[n]≤lk,max[n]

C6:rk[n]≤rk,max[n]

C8:μk∈[0,1]

C9:q[0]=qI,q[N]=qF

C10:‖q[n]-q[n-1]‖2≤(VmaxT)2

其中，

(8)

(9)

2 问题求解

问题P1为非凸问题，为方便求解，可将约束C1与约束C3进行等价替换，将原问题变为

(10)

C2,C4-C7,C9,C10

考虑问题P2仍为非凸问题，采用分块迭代算法进行计算。首先，给定一个满足约束条件的UAV轨迹q，对优化问题进行求解，对变量f、l与r进行优化。其次，设定f、l与r为优化后的变量值，优化UAV轨迹q。最后，返回第一步进行循环直到算法收敛。

2.1 给定UAV轨迹q的问题求解

给定q后，问题变为

(11)

s.t. C1-C7

该问题为凸问题，在不考虑问题求解时间限制，可以用求解效率较低但功能强大的凸优化工具包进行求解。但是，在实际应用中，需考虑问题求解的时间效率，提供一种适用于工程领域的拉格朗日对偶算法对上述问题进行快速迭代求解。

问题P3的拉格朗日对偶函数为

(12)

其中，

式中：λ、β、χ和φ均表示对偶矩阵。

P3对应的对偶函数为

(13)

s.t. C4-C6

则P3的对偶问题为

(14)

s.t.λ,β,χ,φ0

利用对偶分解理论，对偶函数计算可分解为3KN个子问题。对应任意k、n，子问题为

(15)

利用KKT(Karush-Kuhn-Tucker)条件[15]，可得lk[n]的最优解为

(16)

其中，

对于rk[n]，子问题为

(17)

同理，利用KKT条件，可得rk[n]的最优解为

(18)

其中，

(19)

对于fk[n]，子问题为

(20)

得最优解为

(21)

(22)

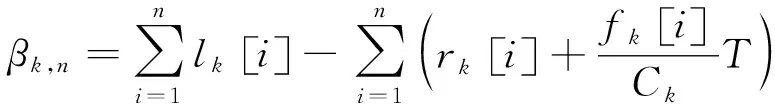
(23)

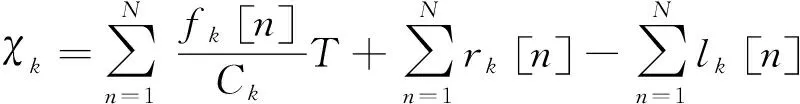
(24)

(25)

2.2 优化UAV轨迹

UAV轨迹优化子问题如下。

(26)

s.t. C5,C6,C9,C10

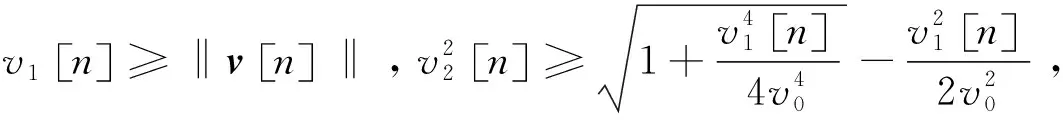
(27)

利用SCA算法，给定v1[n]和v2[n]的任意可行解v1,j[n]和v2,j[n]，非凸约束用凸约束近似为

(28)

其中，

(29)

因此，非凸项由凸项近似代替为

(30)

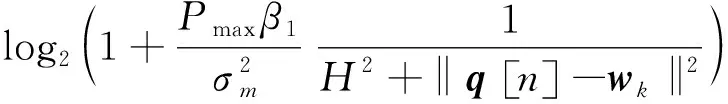
(31)

在式(31)中，

(32)

其中，

同理，将非凸约束C6替换为凸约束

(33)

在式(33)中，

(34)

通过上述分析，问题P7转换为

(35)

C9,C10

步骤1初始化。选择合适步长r[n]∈(0,1]，输入初始可行点矢量为

Ωj[n]=(q(j)[n],v1,j[n],v2,j[n])

n∈QN，令j=0

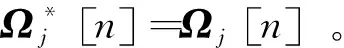
步骤3根据P8计算Ω*(Ωj[n])。

步骤4令Ωj+1[n]=

Ωj[n]+rj[Ω*(Qj[n])-Wj[n]]。

步骤5j←j+1，返回步骤2。

3 实验结果与分析

3.1 仿真的环境和参数设置

对所提的算法进行仿真验证，地面用户随机分布在50 m×35 m范围内，所用其余仿真参数[17]如表1所示。

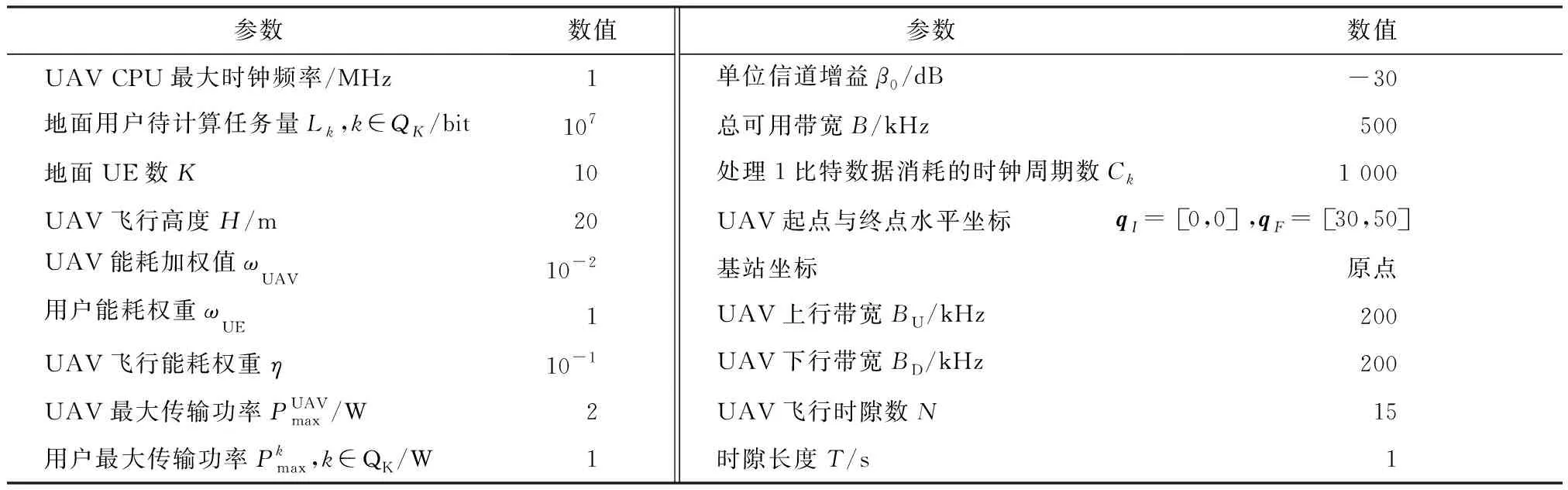
表1 仿真参数

3.2 仿真结果

UAV轨迹与UAV能耗权值ωUAV的关系如图2所示。为测试UAV轨迹与ωUAV的关系，仿真过程中将地面用户集中部署于较为密集的区域。随着ωUAV的增大，系统越来越重视UAV的飞行与计算能耗。因此，UAV会沿着尽可能短的轨迹从起点飞往终点。

图2 UAV轨迹与UAV能耗权值ωUAV的关系

由图2可以看出，随着ωUAV的减小，系统越来越看重地面用户的能耗与任务计算率。ωUAV是UAV能耗权重，ωUAV越大，系统在网络参数优化过程中对UAV能耗的减少更看重。反之，ωUAV减小，则系统在网络参数优化过程中会更看重用户的能耗。因此，ωUAV减小时，UAV会更靠近地面用户所在区域，减少与地面用户的距离，与其建立更好的地空链路，从而减少地面用户能耗。

UAV上行带宽BU与下行带宽BD对系统性能的影响如图3所示。

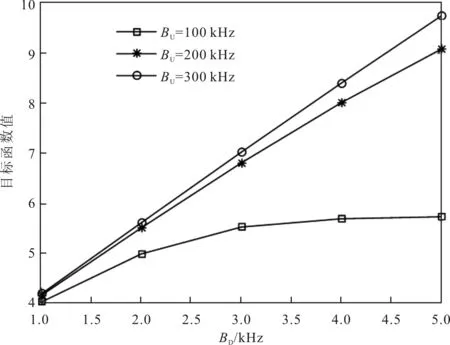
图3 UAV上行带宽BU与下行带宽BD对系统性能的影响

随着上行带宽BU与下行带宽BD的增加，系统目标函数值增加。上行带宽BU增加，地面用户可以卸载更多的数据给UAV。下行带宽BD增加，UAV可以给地面基站卸载更多的数据，提升任务计算率。且由香农公式可知，由于带宽增加，地面用户与UAV在功率方面有更多的决策空间，能耗减少。由图3可以看出，由于受到下行带宽BD的限制，单纯地增加BU并不能无限增加系统性能。在系统设计时需对上行与下行带宽进行综合考虑。

UAV最大飞行速率Vmax与飞行时隙个数N对系统性能的影响如图4所示。

图4 UAV最大飞行速率Vmax与飞行时隙个数N对系统性能的影响

由图4可以看出，随着UAV最大飞行速率Vmax的增加，系统目标函数值增加。由UAV飞行功率表达式可知，UAV功耗与飞行速度有直接关系，悬停或以最快速度飞行并不能获得最低功耗。同时，考虑UAV必须在规定时间内由起点飞往终点，UAV不能以任意速度飞行。Vmax增加，UAV将具有更大的决策空间，从而提升系统性能。飞行时隙个数N越大，UAV具有更多的时间进行飞行与任务计算、卸载，亦可提升系统性能。

4 结语

针对UAV-MEC网络中由于UAV计算能力与能量有限导致其难以完成所有地面用户计算任务的实际情况，研究了一种UAV-MEC网络中地面用户任务完成率与网络能耗加权和最大的系统优化方案。所提方案利用分块迭代、拉格朗日对偶以及SCA算法对所建立的非凸优化问题进行求解，对UAV算力、UAV轨迹、用户卸载任务量与UAV卸载任务量进行联合优化。为了验证所提方案的有效性，通过对所提方案在UAV能耗权重、上下行带宽以及最大飞行速率等不同网络参数下的性能进行仿真测试，当UAV权重减小时，拉近UAV和地面用户的距离，能够更好的优化目标函数。其次，单独增加上行带宽并不能无限增加系统性能，故所提方案综合考虑UAV的上行与下行带宽，能够更好的优化系统性能。最后，更高的UAV的飞行速度与更多的飞行时隙数能够进一步提升UAV-MEC网络系统性能。在下一步研究中将引入人工智能技术对UAV-MEC网络智能资源调度。