基于MEMS阵列的二级融合降噪算法

梁思远，武嘉铭

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

航向姿态系统可以提供姿态角信息，包括俯仰角、横滚角和航向角。航空电子系统、自动驾驶系统和导航系统都需要基于准确的姿态角才能保障系统的可靠运行。航向姿态系统需要从外部获取自身相对于导航坐标系的线加速度和角速度。首先，当获取角速度时利用航姿系统计算出姿态角，更新从载体系到导航坐标系的方向余弦矩阵(Direction Cosine Matrix,DCM)。其次，基于当前时刻的DCM将载体系的线加速度转换到导航系。最后，对导航系的线加速度进行数值积分，根据载体的初始速度和位置可以得到当前时刻的速度和位置信息。

航向姿态系统的误差主要由导航信息的初始值、数值计算过程和惯性器件的误差引起的。低成本MEMS陀螺仪凭借其优势在消费电子领域得到广泛的应用，但其精度较低、随机误差大，难以满足惯性级应用的要求。航向姿态系统在进行姿态解算时，需要对角速率进行积分得到角增量，但在积分过程中，误差会逐渐累积，最终导致姿态角的漂移。为了抑制陀螺仪的随机误差，文献[1]提出了二级卡尔曼滤波，虽然通过两个阶段的滤波可以显著降低陀螺仪的零偏漂移，但在滤波的第二阶段需要加速度计和磁力计的辅助，导致了系统的冗余。文献[2]采用一阶自回归模型(Autoregressive Model，AR)对角速率建模，改进了最优估计过程，降低了数据处理的复杂度，但该模型使用的是时不变参数，动态性能较差。文献[3-4]指出微机电(Micro Electro-mechanical Systems,MEMS)陀螺仪阵列中陀螺仪的数量一般有几十个，虽然可以改善消费级陀螺仪的噪声特性，但丧失了体积和质量上的优势。此外，基于神经网络[5-6]和支持向量机[7-9]等智能算法的降噪方法需要大量的样本数据和训练时间。

针对传统方法需要依赖高精度的模型，或者需要加速度计和磁力计的辅助，以及微机电陀螺仪精度较低、随机误差大的问题，拟提出基于最小方差和递推最小二乘(Recursive Least Squares，RLS)的二级融合算法。首先，对MEMS陀螺仪信号进行经验模态分解(Empirical Mode Decomposition,EMD)，EMD分解后的各阶分量可以认为是平稳的单分量，再采用小波阈值降噪的方法处理各阶分量，基于最小方差和RLS对各阶分量进行二级融合。其次，与均值残差分量叠加得到融合角速率参与航姿系统的解算。最后，通过仿真实验，验证所提算法的有效性。

1 基于MEMS阵列的冗余航姿系统

MEMS陀螺仪阵列系统包括阵列传感器板和数据处理板，其中传感器板由10个MPU9250组成，数据处理板的芯片是STM32H750。传感器板和数据采集板通过接插件相连。阵列传感器板将采集到的角速率等数据通过集成电路总线(Inter-Integrated Circuit,IIC)发送至数据处理板，数据处理板上集成了MEMS阵列融合算法，对各个陀螺仪的角速率数据进行处理，最后输出融合的角速率数据。

STM32H750是STMicroelectronics推出的基于ARM Cortex M7内核的处理器，1 MB～2 MB的Flash，1 MB的静态随机存取存储器(Static Random-Access Memory,SRAM)，最高运行频率可达400 MHz，拥有丰富的输入输出(Input/Output,I/O)接口[10]。MPU9250是InvenSense公司推出的9轴运动处理组件，为一款常见的消费级MEMS。MPU9250内部集成有3轴陀螺仪、3轴加速度计和3轴磁力计，输出都是16位数字量，可以通过IIC接口和单片机进行数据交互，传输速率最高可达400 kHz·s-1。陀螺仪的角速度测量范围最高可达±2 000°/s，具有良好的动态响应特性。加速度计的最大测量范围为±16 g，静态测量精度高[11]。具体的基于MEMS阵列的冗余航姿系统如图1所示。

图1 基于MEMS阵列的冗余航姿系统

传感器阵列采用正反布置，单面5个，MEMS陀螺仪的布局如图2所示。

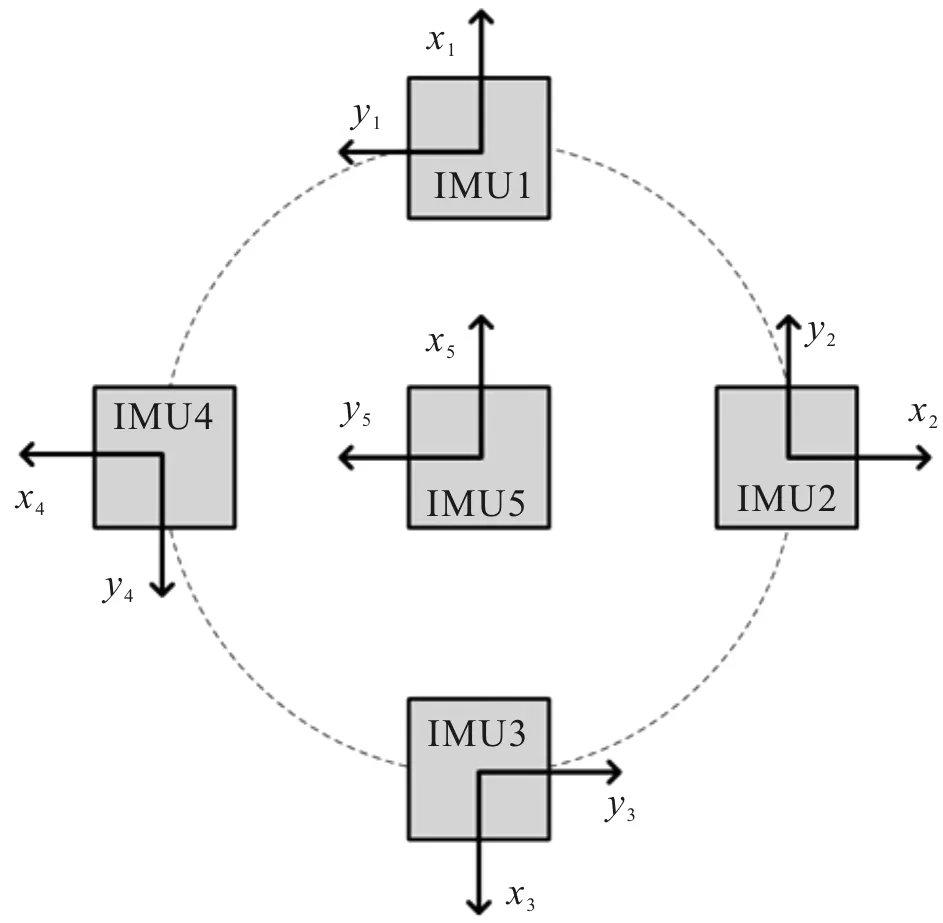
图2 MEMS陀螺仪的布局

反面方向和正面一致，如惯性测量单元6(Inertial Measurement Unit,IMU6)在IMU1的背面，方向一致；IMU7在IMU2的背面，方向一致，等等。阵列中IMU1和IMU2、IMU3、IMU4、IMU5的夹角分别为90°、180°、270°和0°，反面阵列中的IMU方向夹角与正面相同。以IMU1的坐标轴朝向作为整个MEMS阵列组合输出的坐标基准。

2 MEMS阵列的融合算法

2.1 MEMS陀螺仪阵列的误差模型

角度随机游走是MEMS陀螺仪的主要误差源之一[12]，MEMS陀螺仪的误差模型[13]可以表示为

y=ω+η

(1)

式中：y是MEMS陀螺仪的输出角速率；ω是真实角速率；η是随机噪声，表现为角度的随机游走。

于是,MEMS阵列的误差模型可以表示为

Y=Iω+η

(2)

式中：Y=[y1y2…yn]T为输出角速度矩阵，阵列中的每个陀螺是一致的；η=[η1η2…ηn]T表示随机噪声矩阵；I=[1 1 … 1]T表示陀螺仪的配置矩阵。

2.2 基于最小方差和最小二乘的二级融合算法

MEMS陀螺仪的信号具有弱非线性和弱非平稳性。EMD分解具有自适应的特点，且本征模式函数(Intrinsic Mode Function,IMF)分量是平稳的单分量，便于进行小波阈值降噪处理。基于最小方差对各阶分量进行融合，通过RLS估计得到各阶最优IMF分量。对残差分量取平均，将各阶分量和残差分量直接叠加得到最终的融合信号。二级融合算法原理示意图如图 3所示。

图3 二级融合算法原理示意图

下面分别介绍二级融合算法示意图中的信号EMD分解、最小方差权值的确定、最优IMF递推最小二乘估计和信号重构等4个模块。

2.2.1 信号的EMD分解

对MEMS阵列的陀螺仪信号进行经验模态分解，可以得到第m个MEMS陀螺仪的信号为

(3)

m=1,2,…,10

2.2.2 最小方差的权值确定

最小方差估计将估计量看作是观测量的线性组合，以信号的最小方差为准测求待定系数。噪声方差小的信号加权系数大，噪声方差大的信号加权系数小，避免了平均加权的不分优劣的缺点。

(4)

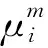
(5)

2.2.3 最优IMF递推最小二乘估计

最小二乘估计不需要任何先验知识，已知被估计量的量测模型即可实现信号参量的估计，且易于实现，同时能使误差平方和达到最小。考虑最小二乘估计必须将所有的观测数据同时处理，当观测数据很多时，其存储和计算量都很大。因此，采用递推的方法，不但可以减少计算和内存消耗，还可以实现实时处理。

(6)

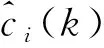
2.2.4 信号重构

将经过最小二乘融合和递推最小二乘估计得到的各阶IMF分量和均值残差分量直接叠加，可以得到最终的信号重构，其表达式为

(7)

重构信号中的各个IMF分量是平稳的，并且都经过小波阈值降噪处理。同时，按照最小方差原则对各个陀螺仪的分量进行加权，有效地抑制了随机躁声。因此，经过降噪预处理的重构信号在进行姿态解算时可以提供更加准确的姿态角。

3 姿态解算

(8)

式中：Q=q0+q1i+q2j+q3，k，i、j、k是虚数单位；ωx，ωy，ωz分别表示陀螺仪的3个轴的角速率。微分方程的求解可以采用双子样算法[17]，即

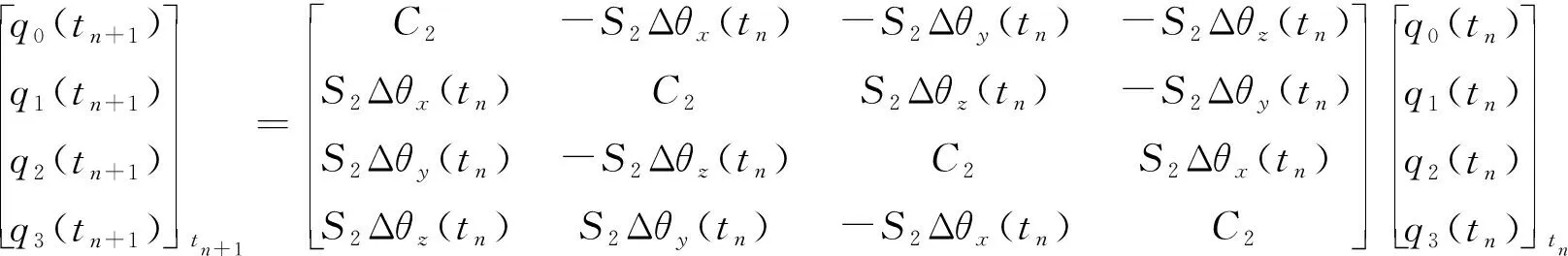
(9)

式中：C2=1-Δθ2/8，表示cosΔθ/2的二级泰勒展开；S2=1/2，表示sin(Δθ/2)/Δθ的二级泰勒展开。为了避免噪声在微分时放大，应直接用角增量确定四元数。Δθx(tn),Δθy(tn)和Δθz(tn)分别为陀螺仪3个轴的角增量及陀螺仪合角增量，表达式分别为

考虑计算误差等因素，计算过程中四元数会逐渐失去规范化特性。因此，若干次更新后，必须对四元数做规范化处理，表达式为

(10)

其中

假设载体的航向角为ψ，俯仰角为θ和横滚角为γ，姿态矩阵中的元素用ψ、θ和γ，则姿态矩阵元素可以分别表示为

T11=cosγcosψ+sinγsinψsinθ
T12=sinψcosθ
T13=sinγcosψ-cosγsinψsinθ
T21=-cosγsinψ+sinγcosψsinθ
T22=cosψcosθ
T23=-sinψsinγ-cosγcosψsinθ
T31=-sinγcosθ
T32=sinθ
T33=cosγcosθ

从姿态矩阵的元素中可以提取出俯仰角、横滚角和航向角，其表达式为

(11)

4 实验验证与结果分析

4.1 Allan方差分析

Allan方差分析法常用于分析陀螺仪的随机误差。陀螺仪误差的Allan方差分析结果可以表示为

(12)

式中：Q表示量化噪声；N表示角度随机游走；B表示零偏不稳定性；K表示角速率随游走；R表示速率斜坡。

使用加权最小二乘进行多元线性回归分析，确定出各种噪声误差系数Ak，即

(13)

各噪声项和误差系数的对应关系，误差系数和Ak的转换关系如表1所示。

表1 误差系数与Ak的转换关系

将航姿系统固定在单轴转台上，陀螺仪采样率设定为100 Hz，室温条件下采集数据1 h，分析数据的Allan方差并绘制双对数图如图4所示。从Allan方差的双对数图可以看出，斜率主要表现为-1/2和0，说明陀螺仪主要受角度随机游走和零偏不稳定性的影响，陀螺仪Allan方差对比情况如表2所示。

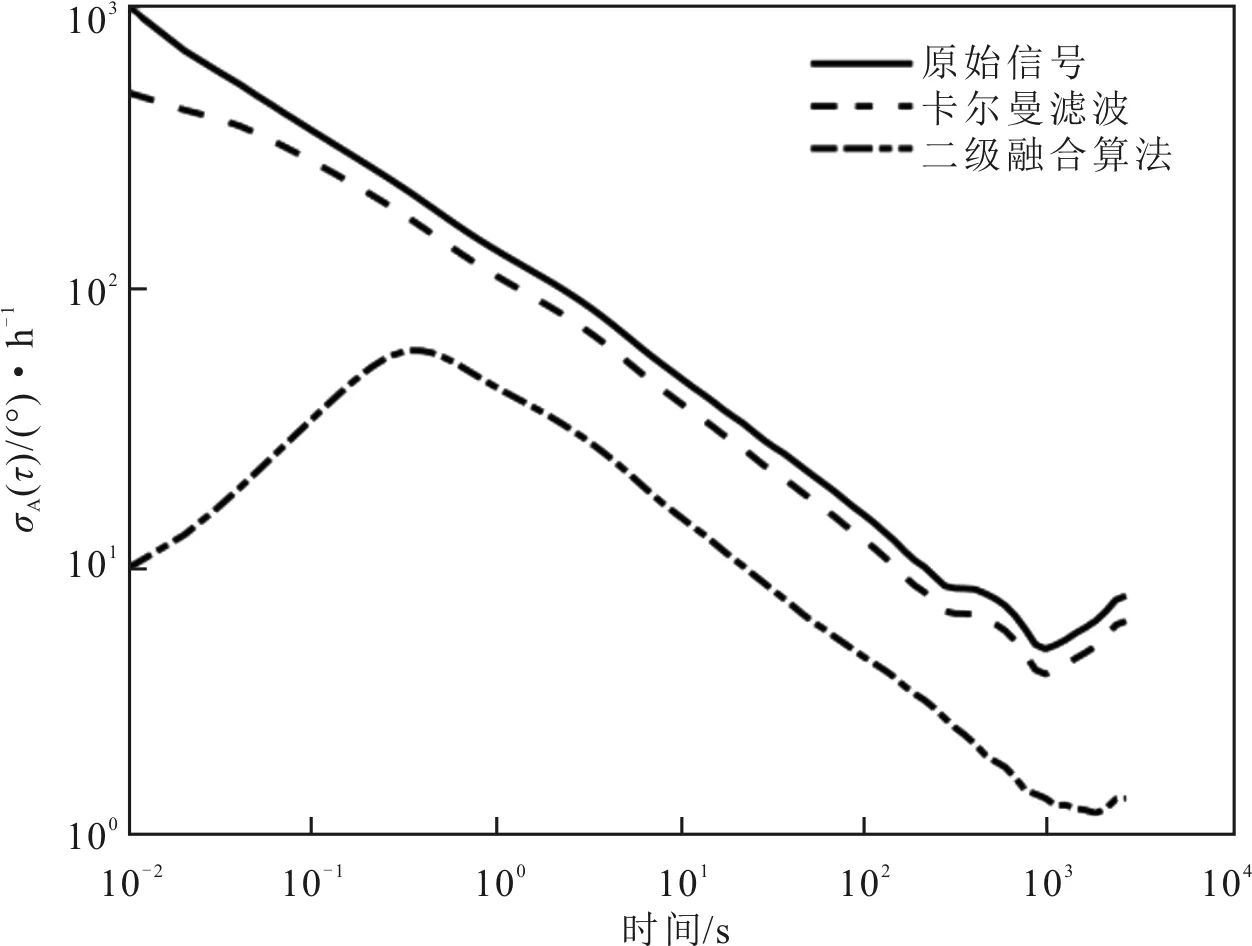
图4 陀螺仪数据的Allan标准差分析

表2 陀螺仪Allan方差对比

所提算法将陀螺仪原始数据的角度随机游走降低了约68%，卡尔曼滤波算法将原始数据的角度随机游走降低了约19%。二级融合算法将陀螺仪原始数据的零偏不稳定性降低了约75%，卡尔曼滤波算法将零偏不稳定性降低了约19%。

4.2 动态性能分析

将航姿系统固定在单轴转台上进行常规多速率实验，采样率设定为100 Hz，通过串口将数据发送至上位机。分析俯仰角、横滚角和姿态角的原始数据和经过二级融合去噪的均方根误差，姿态角均方根误差如表 3所示。使用不同算法得到的姿态角变化曲线分别如图 5、图 6和图 7所示。

表3 姿态角均方根误差

图5 俯仰角变化

图6 横滚角变化

图7 航向角变化

从图5和图6可以看出，经过二级融合算法的处理，陀螺仪俯仰角和横滚角的变化比较平稳。在航向角发生变化时二级融合算法有效抑制了俯仰角和横滚角的震荡。从图7可以看出，航向角在发生变化时，由于误差的积累，导致航向角发生了漂移。点画线表示经过二级融合算法处理的航向角，当航向角由0°变化至负180°时，漂移明显减少，而且效果好于卡尔曼滤波算法。

5 结语

针对航姿系统中MEMS陀螺仪随机误差较大、精度较低的问题，提出了一种基于最小方差和递推最小二乘的二级融合算法。该算法采用最小方差估计出最优的IMF加权系数，再根据递推最小二乘得到最优IMF估计值，最后将各阶分量和残差叠加得到重构信号。为了验证算法的有效性，在静态和动态环境下将二级融合算法和卡尔曼滤波算法进行了比较。实验结果表明,卡尔曼滤波算法可以将角度随机游走系数降低约19%，二级融合算法将角度随机游走系数降低了约68%，二级融合算法与卡尔曼滤波算法相比显著降低了陀螺仪的角度随机游走系数；零偏不稳定性经过二级融合算法处理比卡尔曼滤波算法提高了约56%。在动态性能分析中，所提算法将俯仰角、横滚角和俯仰角的均方根误差分别降低了约98%、98%和84%，比卡尔曼滤波的性能提高了约76%、76%和70%。