两栖车航行阻力特性的数值研究

周利兰 张乐乐

(武汉理工大学 船海与能源动力工程学院∥高性能船舶技术教育部重点实验室，湖北 武汉 430063)

水陆两栖车既具有陆上机动能力，又具有水上航行能力，并且可以依靠自身控制系统由陆入水、由水登陆，在现代军事领域和民用领域都具有广阔的应用前景[1]。两栖车辆作为一种特殊船体，其水动力性能与船舶有一定的相似性，但也有很大的不同。两栖车辆属于钝体结构物，车体结构复杂，流线型较差，航行时兴波和湍流现象严重[2]，阻力特性与常规船舶差异明显。研究两栖车水上航行阻力的构成、成因及变化规律，是两栖车辆论证、研制的重要内容，可为提高两栖车辆的水动力性能提供有力的理论依据。

模型试验和数值计算相结合是研究轮式水陆两栖车水上性能的有效途径。More等[3]通过模型试验和数值计算相结合的方法，对一种轮式两栖战车进行了稳定性和阻力分析，为两栖车辆形状设计提供了参考。对于两栖车辆的动态运动过程，万晓伟等[4]提出ALE(任意拉格朗日-欧拉法)方法解决车辆与水流的动力耦合，实现了车辆航态计算自动化；赵彬等[5]通过对比静态和动态两种网格技术在模拟两栖车辆航行特性时的适用性，证实了动态网格技术相比于静态网格技术的先进性和可行性；蔡宇峰等[6]通过对两栖车实车和模型黏性绕流场进行数值模拟，提出两栖车辆模型与实车水动力性能换算在一定程度上可以采用船舶的弗汝德换算方法。周景涛等[7]采用滑移网格方法实现了两栖车航行姿态的变化，对比了有无防浪板情况下两栖车总阻力和航行姿态的变化规律，结果表明防浪板可有效提高两栖车辆水上航行的稳定性；郭文凤等[8]采用k-ε湍流模型和VOF(Volume of Fraction)两相流模型对轮式两栖车辆绕流场进行了数值模拟，认为轮式两栖车辆防浪板的角度以及车轮是影响其航行阻力的主要因素，为轮式两栖车辆的结构优化及减阻增速研究提供了参考依据。宋桂霞等[9]对车轮收起前后的两栖车辆的黏性绕流场进行了数值模拟，结果表明，在不考虑兴波阻力的前提下，收起车轮可大幅减小两栖车辆的黏压阻力；孙旭光等[10]提出了一种以“改进叠模”为主要技术路线的形状阻力分离方法，获得了两栖车航行阻力的成分构成，该方法可有效分析两栖车的航行阻力。

文中在上述研究的基础上，建立两栖车水上航行运动的数值仿真模型，基于该模型计算两栖车在静水中不同航速下的阻力特性和航行姿态的变化，结合叠模计算结果对两栖车各阻力成分进行了分析；同时，研究了带开口的两栖车模型阻力和航态的变化。

1 数值方法

1.1 控制方程

对于湍流计算问题，采用目前应用最为广泛的求解RANS方程组的数值方法，其控制方程如下。

(1)连续方程

(1)

(2)动量方程

(2)

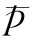
求解上述流动控制方程时，由于雷诺应力项的出现使方程组不封闭，无法求解，因此应选取合理的湍流模型使方程组封闭以求解。

1.2 湍流模型和自由面处理

两栖车在水中运动过程中存在边界层分离现象，并存在车体尾部漩涡结构；Realizablek-ε两方程湍流模型可以计算较为复杂的湍流问题[11]，且该模型对于漩涡流动、强逆压梯度的边界层流动和流动分离都有很好的表现。王涛[12]采用6种湍流模型对两栖车水上绕流场进行了计算和分析，结果表明，Realizablek-ε两方程湍流模型计算得到的总阻力相对误差最小。综上，本研究采用Realizablek-ε两方程湍流模型对两栖车航行阻力进行计算，其湍流动能k方程和湍流耗散率ε方程分别如式(3)和式(4)所示：

(3)

(4)

其中,Gk为平均速度梯度引起的湍流动能的产生项,C1和C2为经验常数,σk和σε分别为k和ε对应的普朗特数，ν为运动黏性系数。

两栖车水上行驶绕流场是气液两相流动问题，且其航速较高，兴波现象明显，计算中需考虑自由液面的影响。VOF方法可用于研究几种互不相溶的流体之间的交界面位置，是目前处理自由表面的一种有效方法[9]，本研究采用VOF法对自由液面进行捕捉。

2 计算模型与网格划分

2.1 数值模型

本研究借助CFD商业软件STAR-CCM+计算两栖车静水直航的水动力性能，缩尺比为5。两栖车模型的主尺度参数为：车长Loa=2.48 m、车宽B=0.71 m、吃水深度T=0.17 m、排水量Δ=200.4 kg；三维模型如图1所示。

图1 两栖车三维模型图Fig.1 Amphibious vehicle model

2.2 计算域及边界条件

计算域的尺寸设定要保证其合理性，计算域太小会影响计算结果的准确度，过大则会带来更高的计算成本。根据对流场模拟计算的需要并参考相关的文献[5]及经验来设置计算域的范围及模型在计算域中的位置。本研究中计算域分为背景域和重叠域两部分，均为长方体区域。其背景域入流边界距离车身首部1.5倍车长，上下边界分别距离车身底部0.75倍和1.5倍车长，侧面边界距离车体中纵剖面1.5倍车长，均设置为速度入口，给定流速值和方向，出口边界距离车身尾部3倍车长，设置为压力出口。由于车身左右对称，且静水航行流场关于中纵剖面对称，因此仅对流域的一半进行网格离散，中纵剖面设置为对称边界。车体物面设置为不可滑移壁面边界条件。具体的计算域及边界条件设置如图2所示。

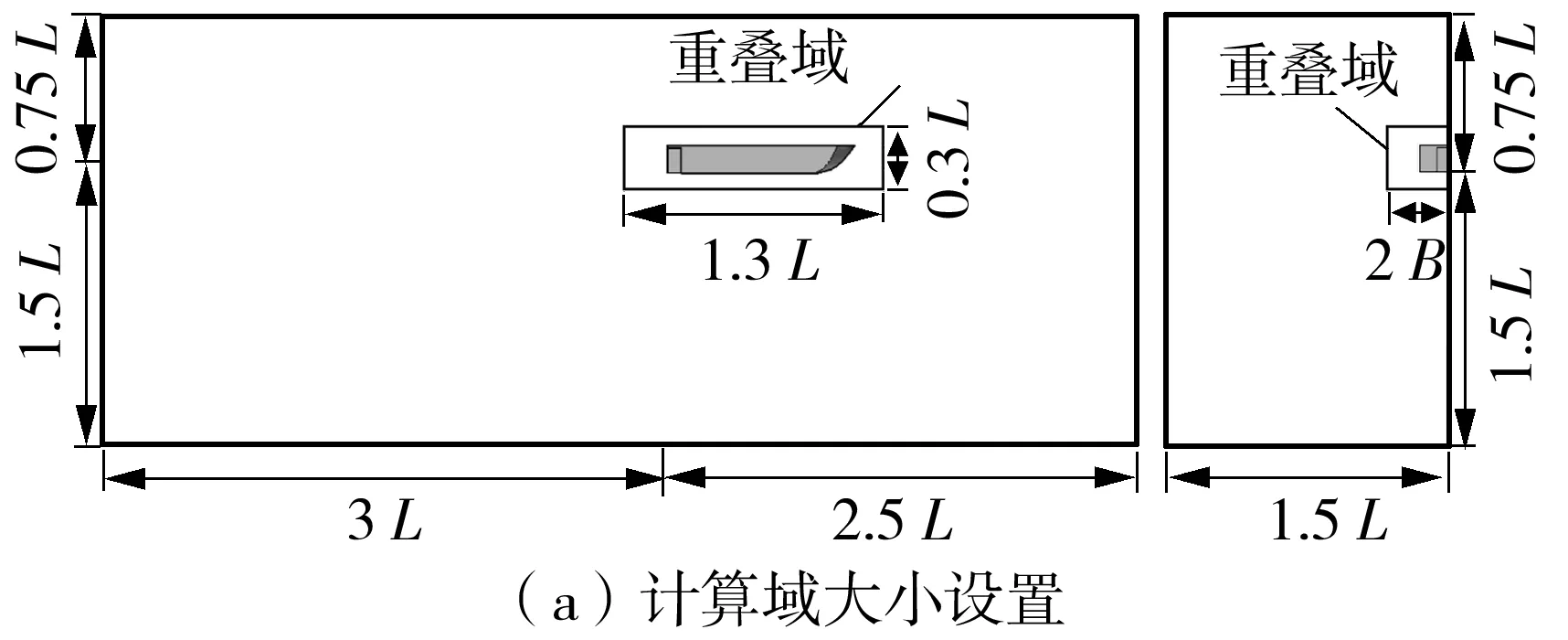
图2 计算域大小及边界类型Fig.2 Computational domain and boundary condition settings

2.3 网格划分

本研究采用重叠网格技术，重叠域在计算过程中会随着物体的运动而运动，在重叠域和背景域之间设置线性交界面条件，将两套网格域连接起来进行数据交换。网格划分采用STAR-CCM+软件自带的前处理工具，使用切割体网格技术对计算域进行网格划分，船体表面采用棱柱层网格以捕捉边界层流动，保证网格法向尺寸满足壁面函数应用的要求。在车首尾以及重叠网格区域进行网格加密，自由液面对计算结果的影响很大，因此必须考虑自由液面的网格加密，尤其是垂向的网格尺寸。最终的网格划分如图3所示，网格总数为206万。

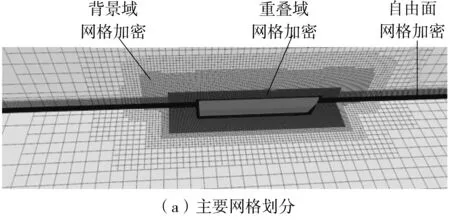
图3 计算域网格划分Fig.3 Grid distribution of computational domain

网格划分后对求解器参数和物理模型进行设置，时间域的离散格式采用一阶隐式方案，湍流模型选用Realizablek-ε湍流模型，自由液面选用VOF方法进行模拟，使用DFBI对运动进行模拟，释放纵向转动和垂向运动两个自由度，时间步长取为0.02 s。

3 数值不确定度分析

图4 不同网格方案Fig.4 Different grid schemes

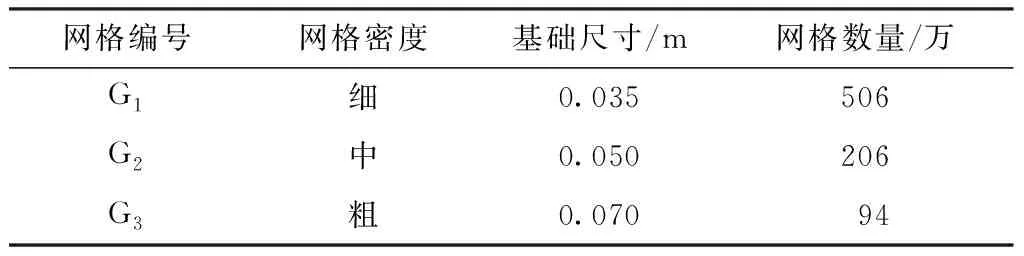
表1 不同网格的基础尺寸及网格数量Table 1 Basic mesh size and number of mesh

表2给出了3套网格方案下两栖车模型在Vm=2.485 m/s时总阻力的计算值Rt和试验值D，模型试验在武汉理工大学拖曳水池进行，车体航行时所受阻力通过阻力仪记录，车体航行时的纵倾角通过倾角仪记录，导航杆用于约束两栖车的横向运动，试验中释放两栖车的纵摇和升沉两个自由度。不确定度分析过程中的验证因子(收敛率RG、准确度阶数PG、修正因子CG、网格不确定度UG)见表3。

表2 不同网格方案的阻力计算结果对比Table 2 Comparison between experimental results and simulated results with different grid configuration

表3 验证因子Table 3 Validation factors

1)UG的值以D为基准计。

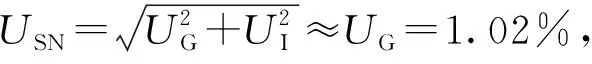
4 阻力成分的确定

两栖车的车体型线与船舶有很大差别，对于大多数航速较低的两栖车辆，其水上航行阻力主要以黏压阻力为主，兴波阻力和摩擦阻力所占比例较小，随着航速提高，兴波阻力所占比例会逐渐增加。

两栖车各阻力成分的确定方法如下：摩擦阻力Rf是作用在车体湿表面积上全部切向力的总和，其值可由CFD软件直接计算得出；兴波阻力Rw是由于车辆在航行过程中产生的波浪引起车体周围的压力分布改变所产生的阻力[14]，本研究通过对带自由面的两栖车黏性绕流场进行数值模拟，得到两栖车总阻力Rt，再结合叠模计算方法，将自由面设置为对称平面，以消除自由面兴波带来的影响而得到黏性阻力，继而可以通过总阻力Rt扣除黏性阻力得到兴波阻力；黏压阻力Rvp是由于流体黏性和车体后部流体的纵向压力梯度所形成的阻力，可通过公式Rvp=Rt-Rf-Rw计算得到。采用叠模方法进行计算时，叠模模型的初始航态按照带自由面的两栖车黏性绕流场计算中得到的航行姿态进行设定。模拟中除了将计算域顶部设置为对称面，不考虑自由表面的影响外，叠模方法中计算域的大小及其他边界的条件设置均与带自由面的两栖车绕流场的模拟一致。

5 计算结果与分析

5.1 无开口两栖车模型的计算结果与分析

在数值方法验证和确认的基础上，采用相同的数值方法对两栖车静水直航运动进行数值模拟。随着航速提高，两栖车的航态会因流动支持力比例的变化而发生变化，吃水深度和水线长度也随航速的变化而变化，通常用与船舶质量相关的体积傅汝德数表示船的相对速度，体积傅汝德数定义如式(5)所示。

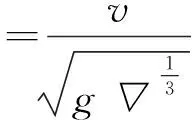
(5)

式中：v为航速，m/s；g为重力加速度，取值为9.81 m/s2；▽为两栖车的排水体积，m3。

不同体积傅汝德数对应的实车和模型航速如表4所示。

表4 不同Fr▽对应的两栖车实车及模型航速Table 4 Speed of full-scale and model amphibious vehicles with different Fr▽

不同航速下两栖车模型的阻力计算结果与试验结果的对比如图5所示。从图5中可以看出，数值计算的总阻力与试验值基本一致，在实车航速为20 km/h(Vm=2.485 m/s)时误差不到1%。

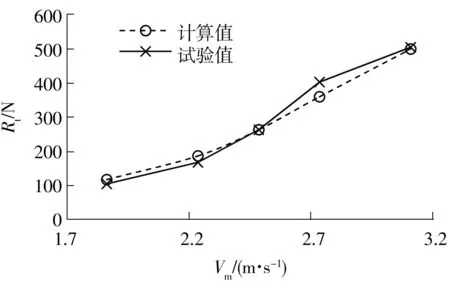
图5 数值模拟与试验结果的对比Fig.5 Comparison between numerical simulation and experimental results

不同航速下两栖车模型的阻力和航态的计算结果如表5所示；其中，升沉量Δd为负代表吃水增加，纵倾角θ为负代表尾倾。

由表5可以看出，随着航速的增加，两栖车总阻力、纵倾角和下沉深度逐渐增加。两栖车航行速度越高，水流流经车体底部的速度越大，造成车底压力降低，车体受到的浮力减小，吃水增大；当吃水增大到一定程度后开始减小，这是因为随着航速增加，当Fr▽>1以后，两栖车达到过渡航态，静浮力的成分有所减小，流体动升力逐渐增大，进而使车体吃水有所减小。同时，航行速度越高，车体首部受到的水流的冲击作用越大，首部受到的浮力与尾部受到的浮力不相等，产生纵倾角的变化也会越大。

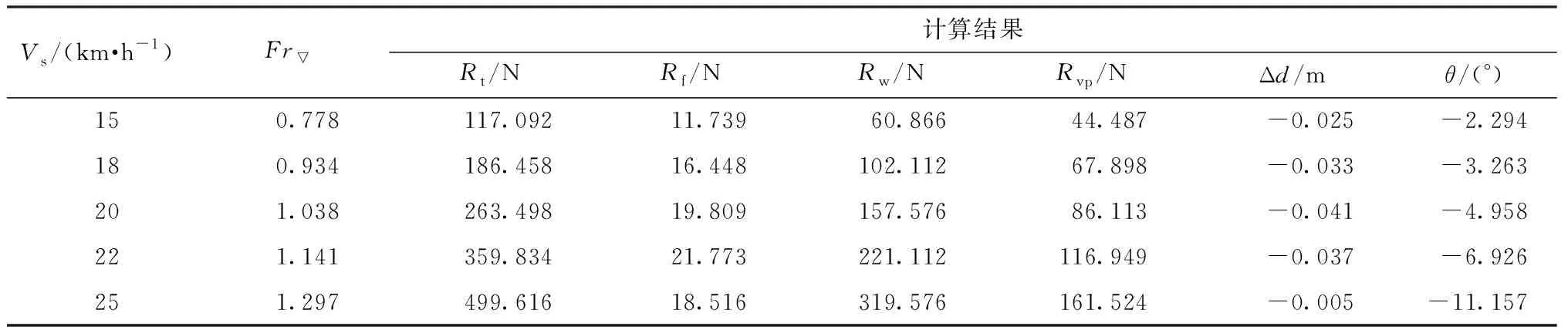
表5 不同航速下两栖车模型的阻力和航态的计算结果Table 5 Calculation results of model resistance and navigation attitude at different velocities

不同速度下车体达到稳定航行后的水气两相云图如图6所示。从图6中可以看出，车体纵倾角随航速增加而增大，在Fr▽=1.297时车体抬首现象严重；结合表5所示结果可以看出，纵倾角的变化速率也随航速的增加而增大，特别是当Fr▽>1之后，尾倾显著增加。

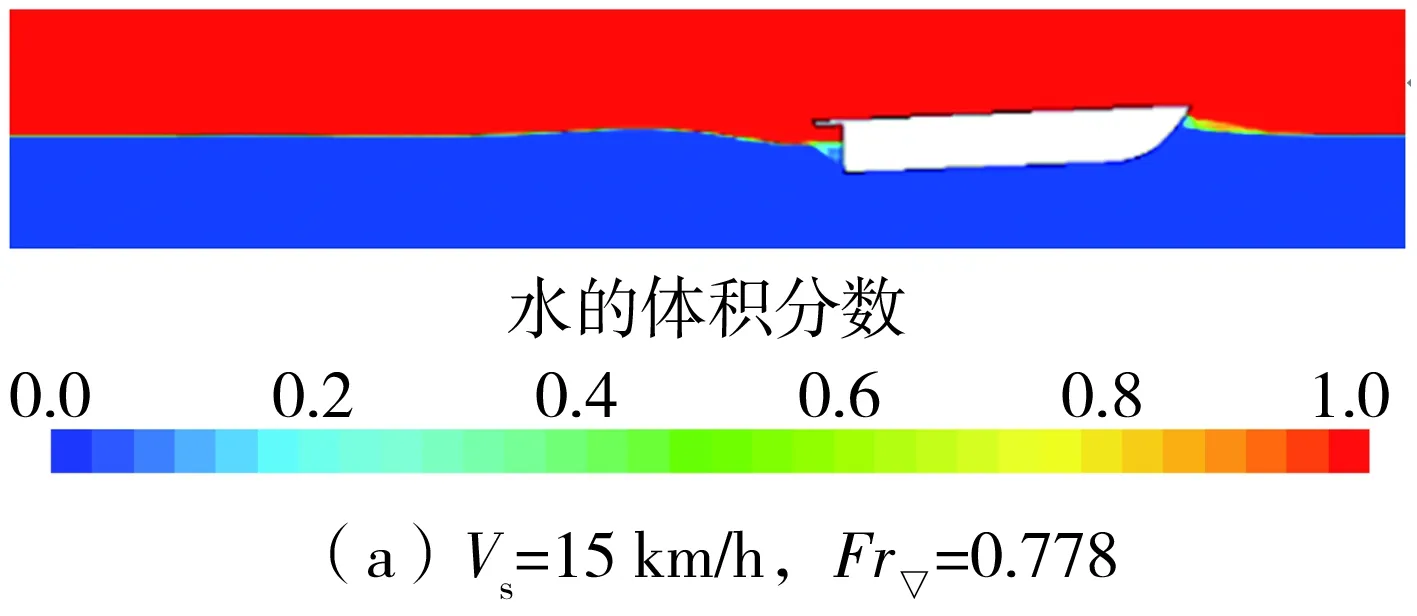
图6 不同航速下两栖车模型的水气两相图Fig.6 Water-air two phase diagram of model with different velocities

图7所示为各阻力成分的值随Fr▽的变化情况。由图7可以看出，兴波阻力和黏压阻力随Fr▽增大而增加，摩擦阻力增大到一定程度后开始有减小趋势，其原因是Fr▽>1后，车体吃水减小，湿面积减小使得摩擦阻力开始减小。从图8所示的各阻力成分占比上看，对于航行速度较高(即Fr▽较大)的两栖车，水阻力以兴波阻力为主，所占比重在50%以上；黏压阻力占比在30%～40%之间；摩擦阻力占比较小，不超过10%。随着航速的提高(即随着Fr▽的增大)，黏压阻力比重稍有所下降，到过渡阶段后基本保持不变，而兴波阻力的比重逐渐增大伴随着摩擦阻力比重下降。

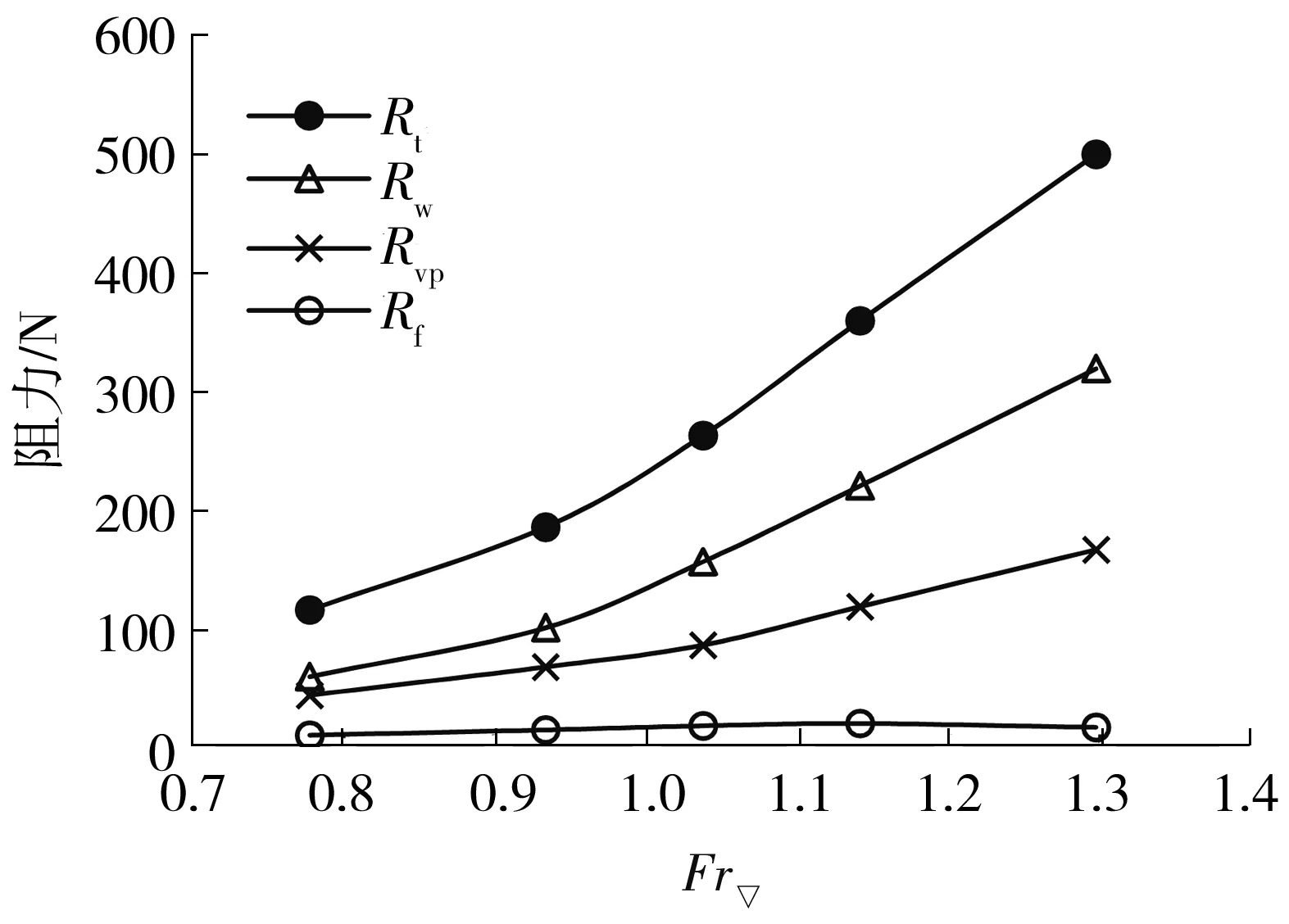
图7 两栖车模型的各阻力成分随Fr▽的变化曲线Fig.7 Variation curves of resistance components of amphibious vehicle model with Fr▽

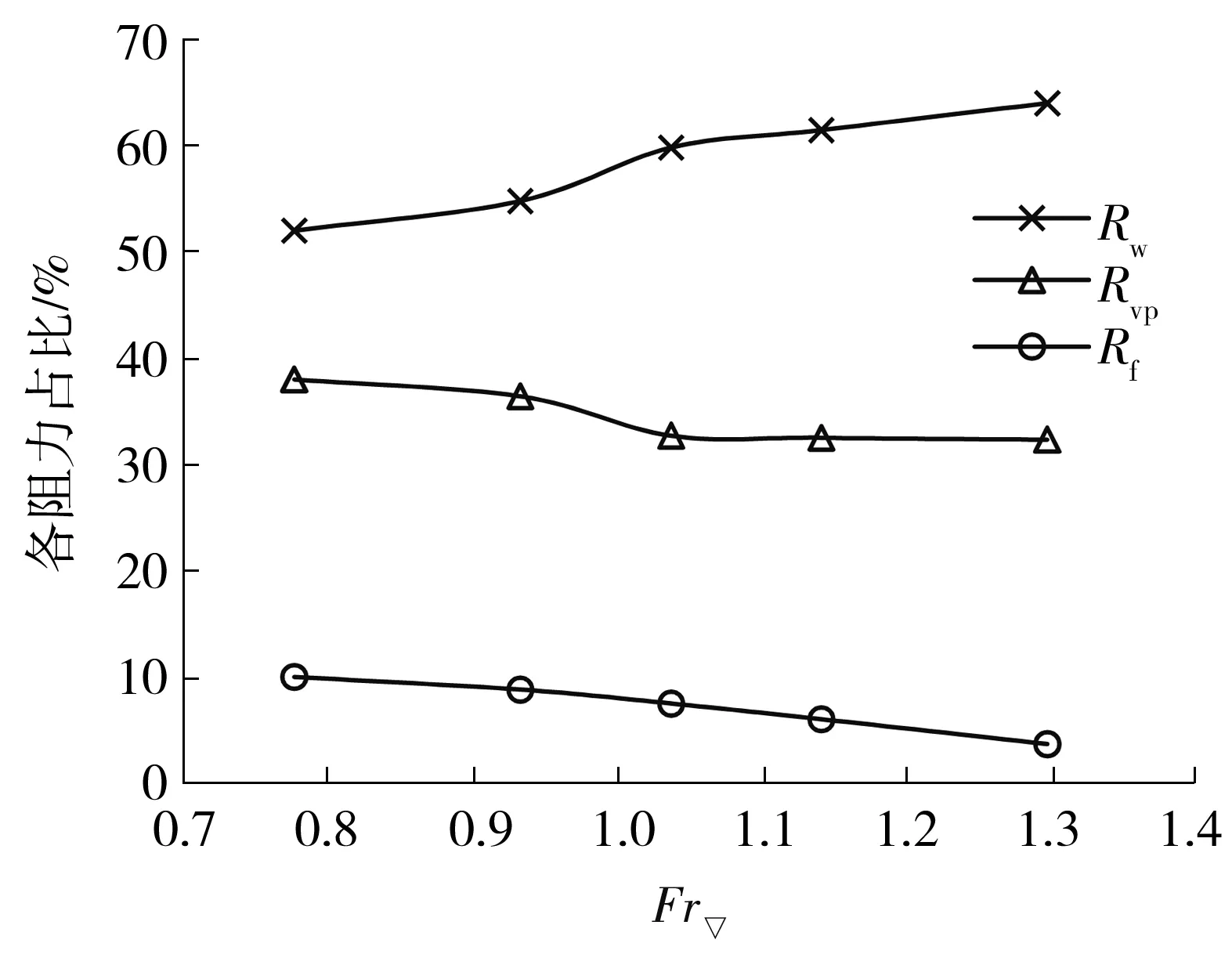
图8 各阻力成分所占比例随Fr▽的变化曲线Fig.8 Variation curves of ratios of resistance components to total resistance with different Fr▽

因为两栖车设计需要考虑车辆的陆地行驶性能，故车体一般呈现为非流线型体，车体尾端曲度变化剧烈[15]，这对两栖车水上航行时的水动力性能有较大影响。图9为Fr▽=1.038时两栖车模型纵剖面航行流场的速度矢量分布情况，从图中可以看出，由于车体形状的急剧变化而引起的突然去流在车体首部和尾部会发生流动分离，并伴有大尺度的漩涡形成，漩涡的存在会造成该区域压力骤降，其在尾部形成的漩涡将会大幅度增加黏压阻力，从而增加两栖车的航行阻力。

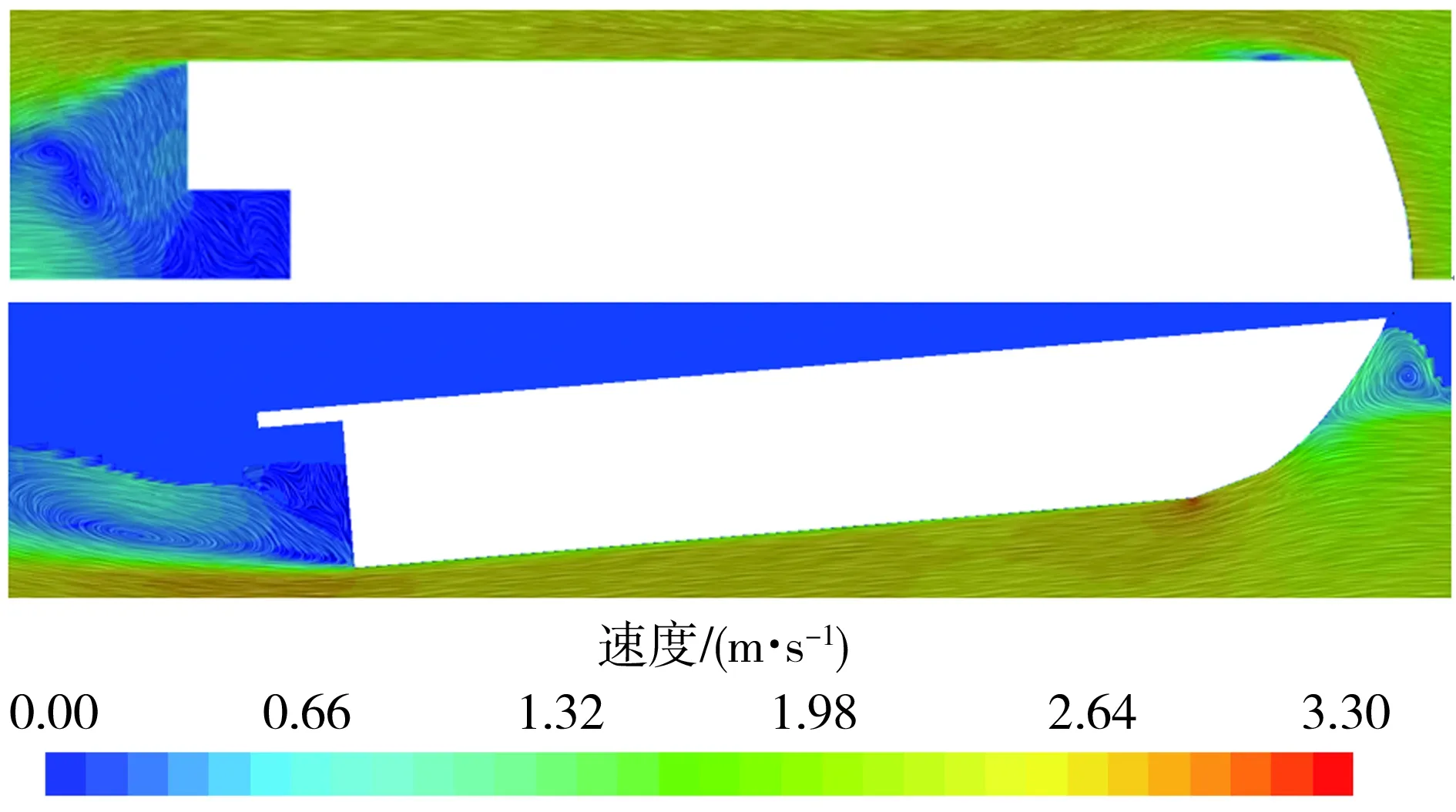
图9 两栖车纵剖面速度矢量分布图(Fr▽=1.038)Fig.9 Velocity vector distribution in the longitudinal section of amphibious vehicle(Fr▽=1.038)

车体中纵剖面周围的压力分布和车底压力分布如图10所示。从压力云图可以看出，在车体首部近水面处形成明显的高压区，车首下方向车底的过渡区域存在一个负压区域，且这一区域的压力梯度很大。从整个流场来看，车首、尾附近为高压区，而车体中部靠前为相对低压区，这是产生车体绕流阻力的主要原因，同时随着航速增加会造成车体纵倾角增大。

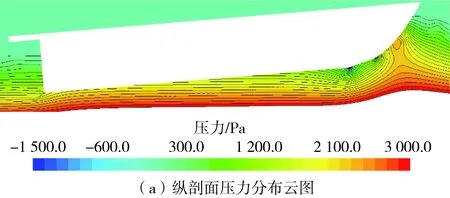
图10 两栖车模型压力分布云图(Fr▽=1.038)Fig.10 Pressure distribution of amphibious vehicle(Fr▽=1.038)

图11(a)为两栖车辆在Fr▽=1.038时的自由液面波形图，图11(b)为车体侧面y=0.36 m处的纵切波形Hw。从图中可以看到，车体首部存在一个较大的波峰，车体尾部呈现一波谷，首尾的流体动压力差导致了较大的兴波阻力；随着航速的增加，首尾的压差增大，兴波阻力增加。

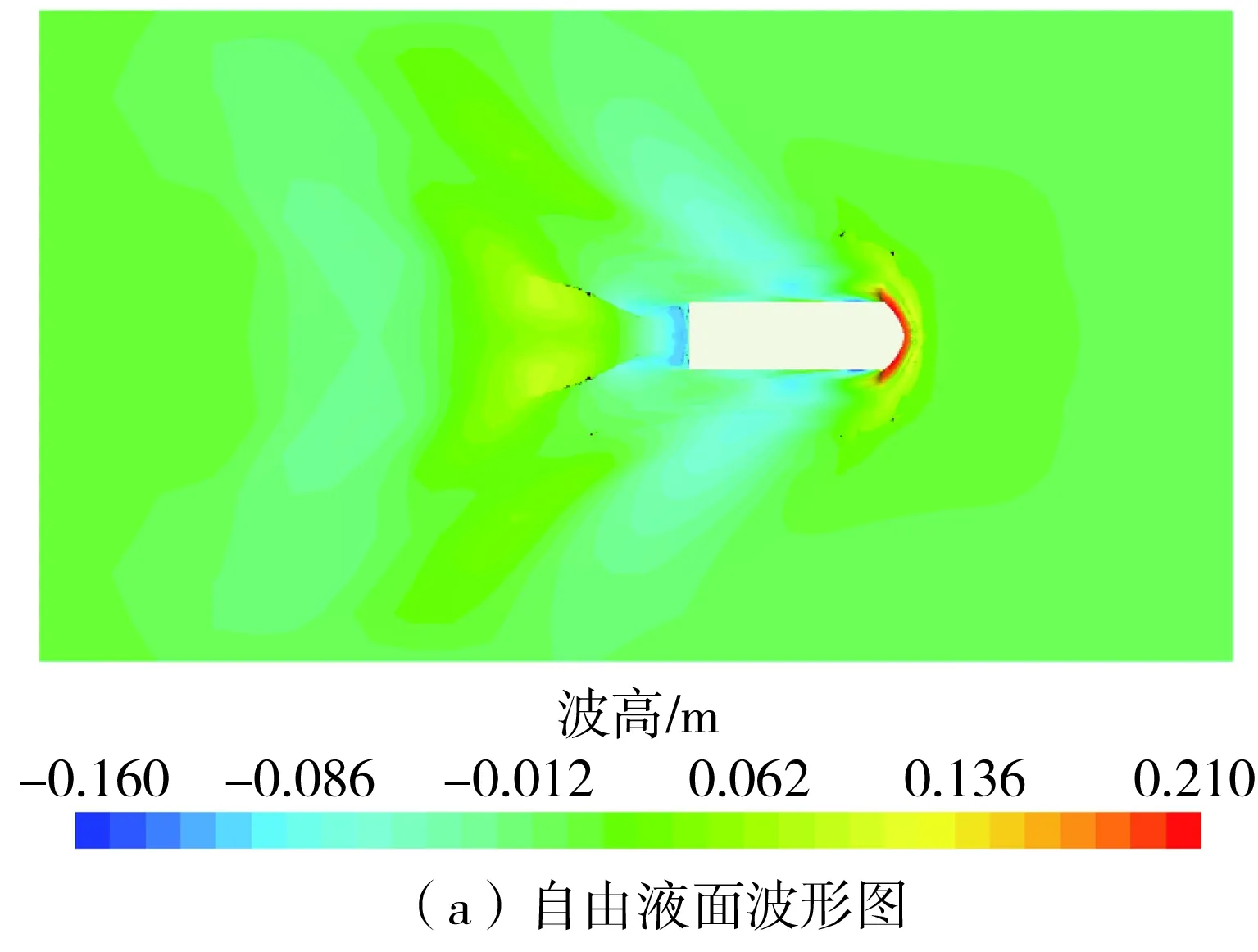
图11 两栖车模型波形图(Fr▽=1.038)Fig.11 Wave pattern of amphibious vehicle(Fr▽=1.038)

5.2 有开口两栖车模型的计算结果与分析

在前文的讨论中，假定行动系统是封闭起来的，而实际上很难做到车轮收起后车体无任何开口，因此对有开口两栖车模型的阻力特性进行计算分析十分必要。图12为有开口两栖车的模型图，开口位置和大小对应车轮位置和大小，开口外沿距离车侧10 mm。

图12 有开口两栖车模型图Fig.12 Amphibious vehicle model with openings

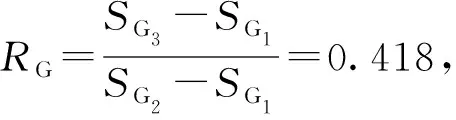
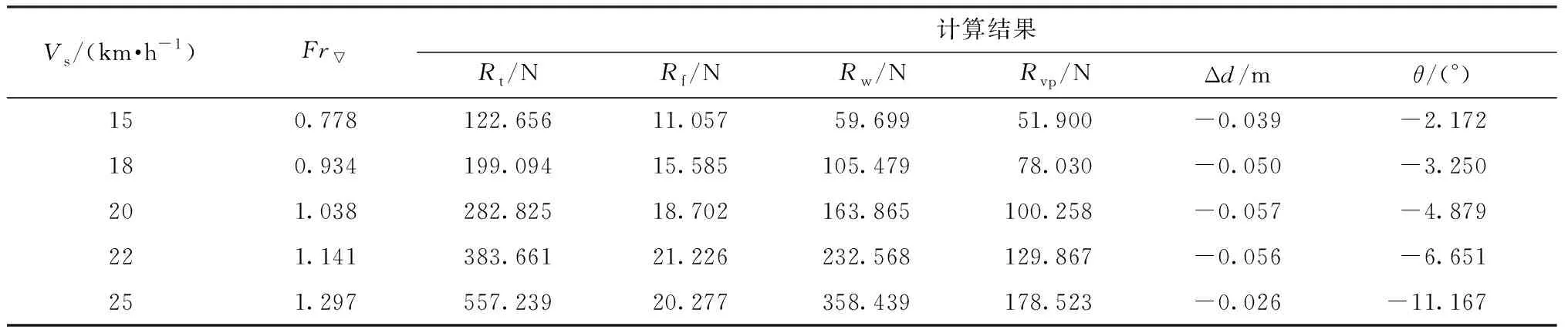
表6 有开口两栖车模型的阻力和航态计算结果Table 6 Calculation results of resistance and navigation attitude of model with openings

有无开口的两栖车模型总阻力计算结果对比如图13所示。从图13中可以看到，增加开口后，两栖车模型的总阻力有所增加。总阻力的增量随着Fr▽的提高而增大，在Fr▽=1.038时，总阻力增加约7%；在Fr▽=1.297时，总阻力增加约11.5%。

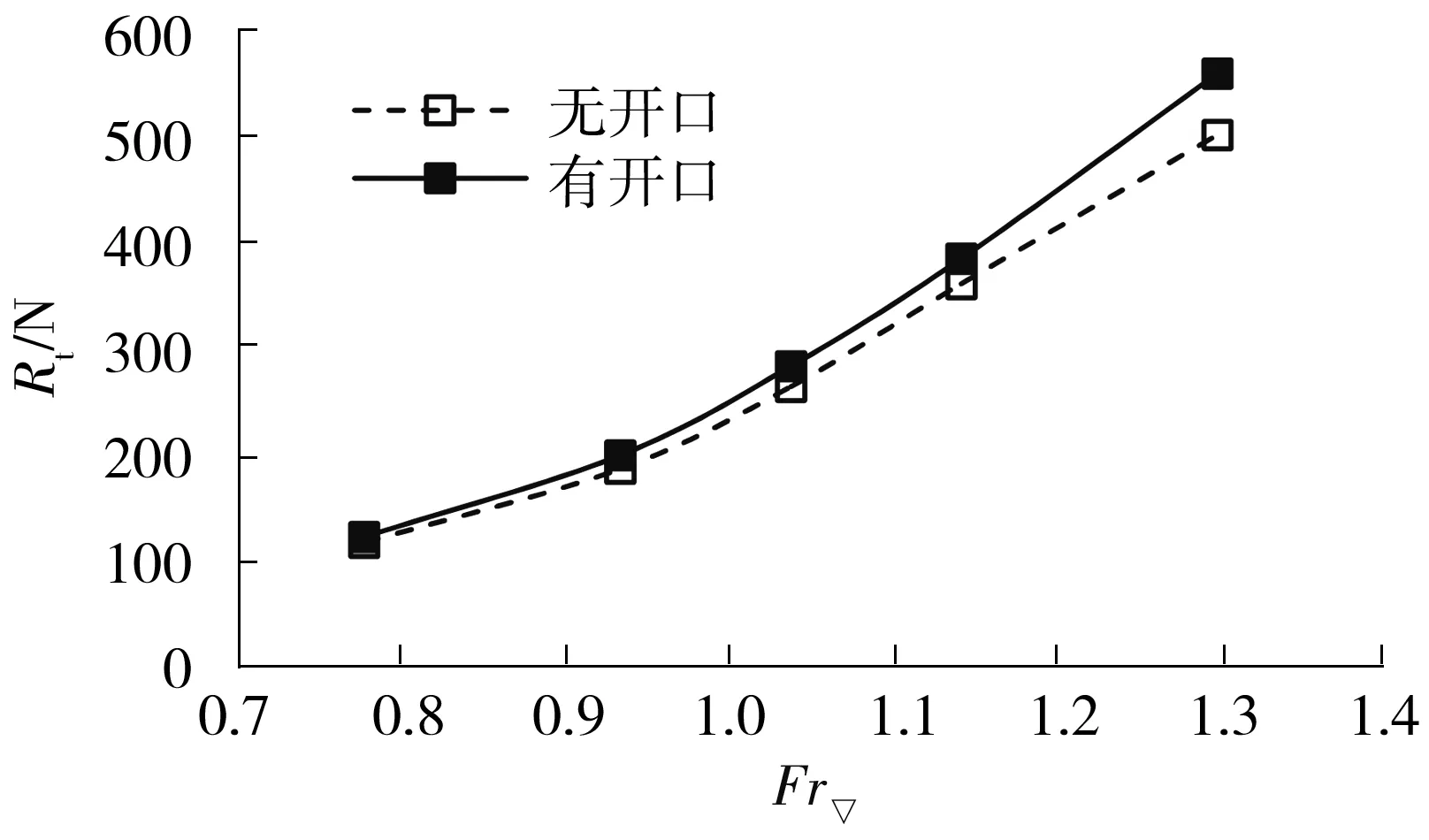
图13 有无开口的两栖车模型总阻力对比Fig.13 Total resistance comparison of models with and without openings

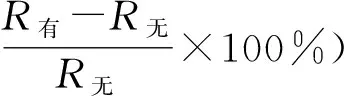
图14 有无开口的两栖车模型各阻力成分对比Fig.14 Different resistance compoents comparison of models with and without openings

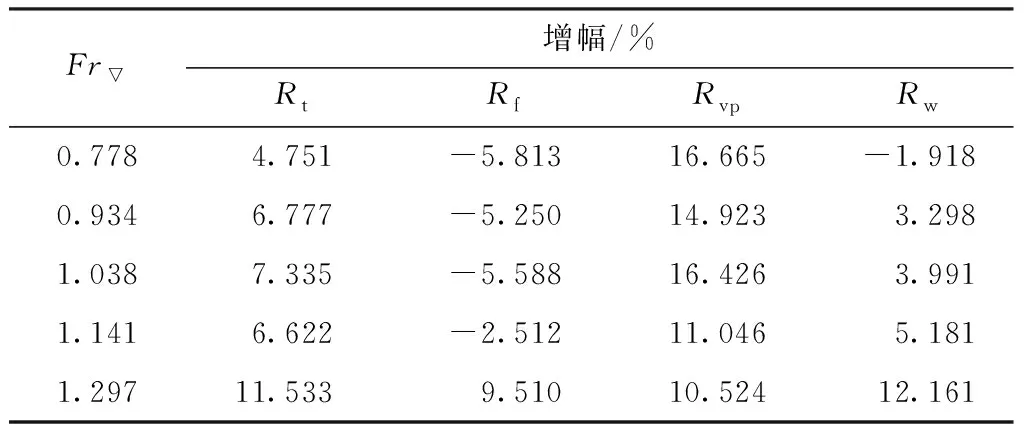
表7 有开口两栖车模型各阻力成分的增幅Table 7 Increase percentages of different resistance compoents of models with openings

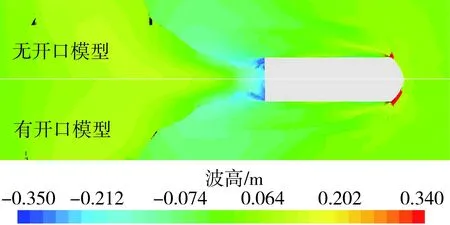
图15 有无开口的两栖车模型的自由液面波形图对比(Fr▽=1.297)Fig.15 Free surface wave pattern comparison of models with and without openings(Fr▽=1.297)

为研究有开口两栖车模型阻力变化的原因，对流场的压力和速度矢量分布情况进行分析。平行于水流方向做一过轮穴区域的截面，在后处理中显示截面处压力分布和流速情况，图16-18分别是有无开口的两栖车模型的截面压力分布、车底压力分布对比和有开口两栖车模型的速度矢量分布图(Fr▽=1.038)。

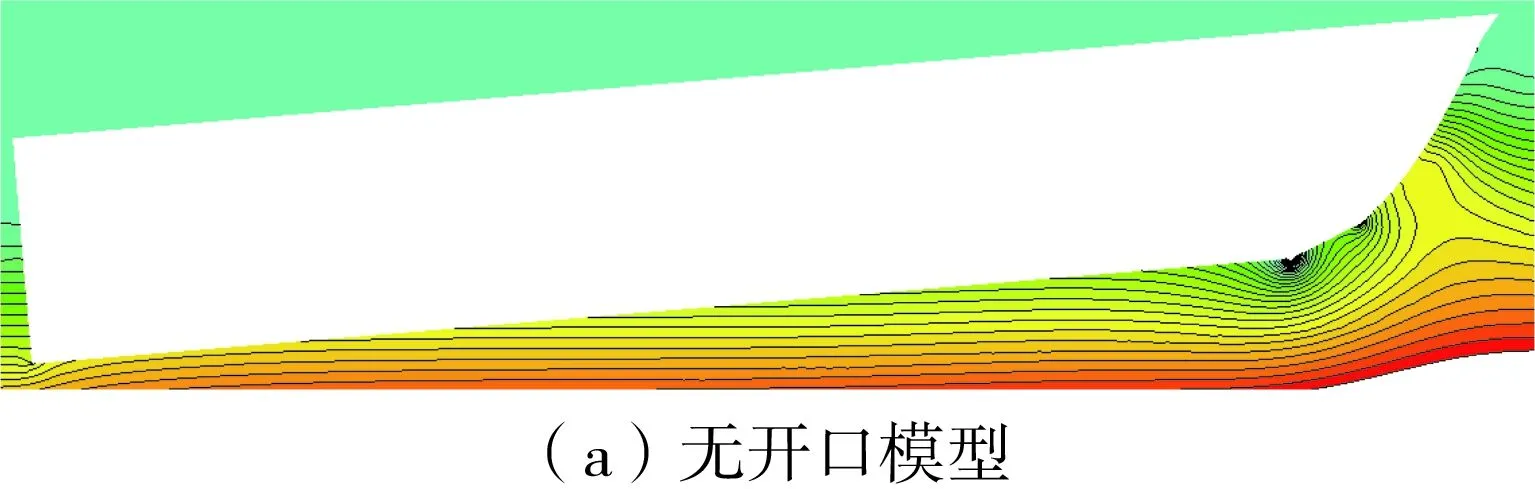
图16 有无开口的两栖车模型的纵截面压力分布对比Fig.16 Comparison of pressure distribution of the longitudinal sections of models with and without openings

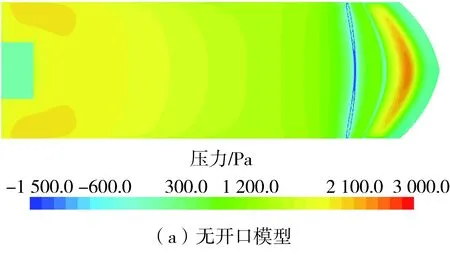
图17 有无开口的两栖车模型的车底压力分布对比Fig.17 Comparison of pressure distribution at bottom of amphibious vehicles with and without openings

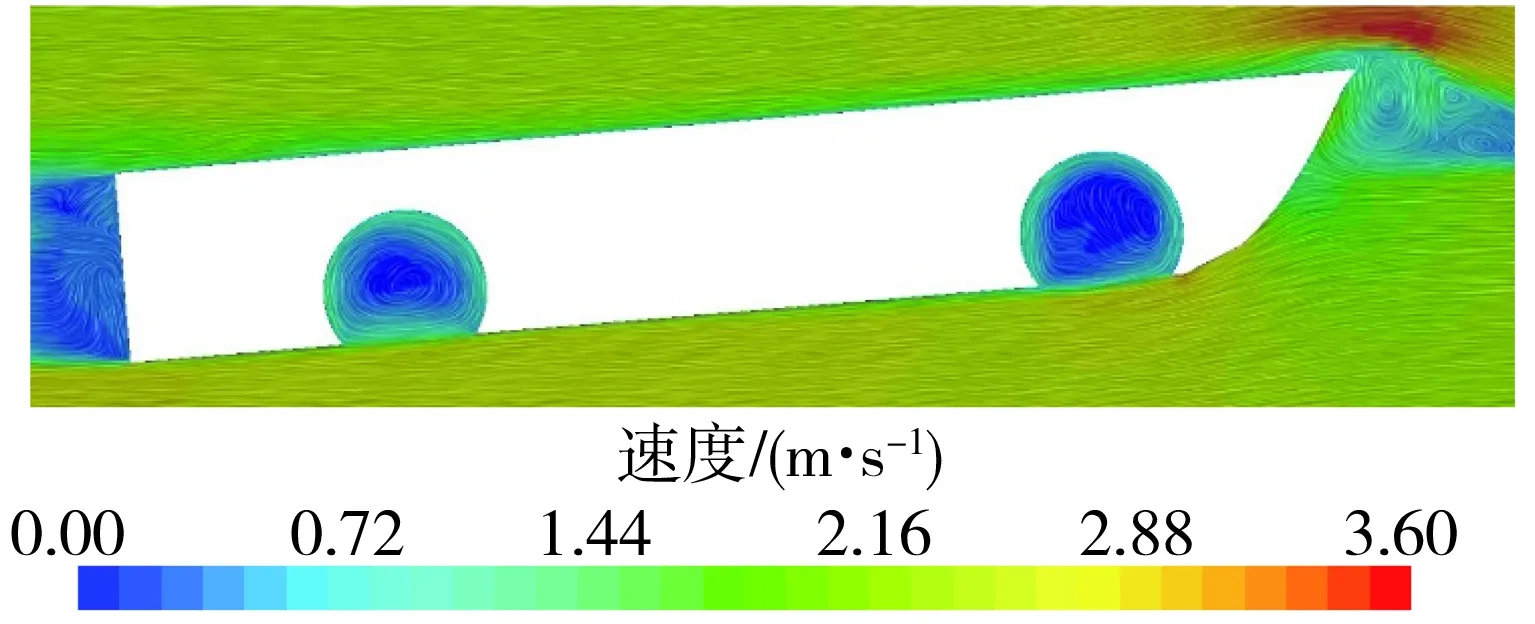
图18 有开口模型的速度矢量分布图Fig.18 Speed vector distribution of models with openings

从图中可以看出，增加开口后，开口内部出现低压区，开口边缘压力变化梯度大，并且在前轮开口产生了负压，轮穴内部相当于一个低压空穴，水流速度降低，开口内部出现大尺度的流动漩涡，相比增加开口前产生了更多的涡流损失，增大了黏压阻力，同时压差阻力的增大也会造成车体下沉深度进一步增加。

6 结语

本研究对静水中有无开口的两栖车模型不同航速下的阻力及航态进行了计算与分析，得到了以下结论：

(1)无开口状态下两栖车的阻力的计算结果与试验结果基本一致，文中采用的数值模型具有可行性。

(2)随着航速的提高，两栖车总阻力逐渐增大；对于处在过渡阶段的两栖车，兴波阻力所占比重在50%以上；黏压阻力占比在30%～40%之间，摩擦阻力占比不超过10%。

(3)增加开口后的两栖车阻力增加，其中摩擦阻力相比无开口模型略有减小，黏压阻力和兴波阻力增大;从阻力成分上看，黏压阻力占比有所增大，兴波阻力和摩擦阻力占比有所减小。

(4)通过有无开口的两栖车模型阻力的对比，发现将车轮部分收起并封闭起来可以使车底压力过渡平稳，减小涡流损失，有助于减小航行阻力。

在本研究基础上可进一步分析车体形状和车轮收放状态对航行阻力和绕流场的影响，为两栖车辆车体结构优化设计提供一定的指导作用。