基于扩张状态观测器的智能船舶循迹预测控制

徐海祥 李超逸 余文曌 韩素敏 魏跃峰 杨素军

(1.武汉理工大学 高性能船舶技术教育部重点实验室，湖北 武汉 430063；2.武汉理工大学 交通学院，湖北 武汉 430063；3.中国船舶及海洋工程设计研究院 喷水推进技术重点实验室，上海 200011)

自20世纪90年代起，以信息技术为核心的高新产业迅猛发展，经济全球化的格局逐渐形成。海上运输因其具有运输量大、成本低廉等优势，在国际贸易运输中占比达到66%，我国外贸海上运输占比更是高达90%[1]。为贯彻“绿色船舶”理念，智能船舶相关技术的研究受到了广泛关注。

2020年我国发布了《智能船舶规范(2020)》，其中明确规定智能船舶需拥有在开阔水域、狭窄道口、进出港口、靠离码头等不同场景下自主航行的能力，以及在复杂环境作用下的自适应能力。同时规定智能船舶自主航行设计过程中，应以船舶航行安全为前提，优先考虑船舶推进和操舵能力，优化船舶在转向点处的航行状态，使其与船舶推进和操纵性能相匹配。因此，航迹控制作为智能船舶自主航行中最重要的工作模式之一，对控制技术提出了更高的要求，如何优化船舶航行时的控制输出以确保船舶自主航行时的安全以及如何保障船舶在海上复杂环境下的高精度航行成为了当前的研究热点。

针对复杂环境扰动补偿问题，韩京清[2]最早提出自抗扰控制方法，该方法能有效估计补偿系统内部不确定扰动和外部环境干扰。2011年，赵大威等[3]首次将自抗扰控制(Active Disturbance Rejection Control,ADRC)引入无人船状态估计模块中，设计了非线性扩张状态观测器。Li等[4]于2013年设计了一种将ADRC与滑模控制方法相结合的滑模自抗扰控制器来补偿船舶循迹时的内外部扰动。Bidikli和Wondergem等[5- 6]考虑到实际工程中速度反馈不准的问题，结合状态观测器与反馈控制律，估计船舶航行速度。2015年，Fu等[7]利用ESO观测器估计补偿船舶模型不确定性和外部干扰构成的复合扰动。Cui等[8]于2017年运用Lyapounv函数设计自适应控制器，并与状态观测器相结合。2019年，沈智鹏等[9]同时引入动态面控制和扩张状态观测器设计控制律,既消除“微分爆炸”问题，也较好补偿了船舶受到的复合扰动。但上述方法对控制输出的优化能力有限。

模型预测控制是当前用来解决优化问题最常用的控制方法。1999年，Wahl等[10]首次于船舶跟踪控制中设计单个自由度的模型预测控制器。2014年，Liu等[11]将控制约束设计进入非线性模型预测控制器中，实现欠驱船舶运动控制。2015年，柳晨光等[12]考虑到船舶运动过程中受到的环境干扰、模型摄动等问题，将MPC与ESO相结合，以实现路径跟踪控制精度的提升。2018年，钱小斌[13]使用反馈线性化方法，利用李导数将船舶非线性模型线性化。文献[14- 15]采用广义预测控制算法，提高控制精度，降低稳态误差。Liu等[16]提出了一种带有扰动观测器的三阶模型预测控制方法，有效估计补偿环境扰动的影响，并为后端执行机构提供了平滑的控制输出。

综上所述，将控制器与状态观测器相结合，是目前研究船舶航迹控制方法的热门趋势，既提高了船舶在复杂环境下的自适应能力，也保证了船舶航行时的安全性、稳定性。

针对ADRC及MPC控制器的稳定性已有学者进行了理论分析。Guo等[17- 18]对线性扩张状态观测器及非线性扩张状态观测器的无穷时域稳定性进行了证明，Mayne等[19]则对无穷时域下的模型预测控制稳定性进行了分析。然而，针对级联系统的稳定性证明无法直接通过各子系统单独证明获得。1998年，Elena等[20]提出了非线性分离式原理，为级联系统的稳定性证明提供了理论基础。2017年，瞿洋[21]基于非线性分离式原理，证明了带有无源观测器的PID级联控制器的稳定性。

受上述工作的启发，文中通过设计非线性ESO-MPC级联控制器，对船舶循迹时受到的复杂时变多源干扰进行补偿，并考虑推进器性能，进行控制输出的优化；同时，基于非线性分离式原理，证明所设计级联控制器的稳定性；最终，通过与ADRC及MPC控制器进行仿真对比，对该级联控制器的有效性进行验证。

1 船舶模型建立

为便于描述船舶水平面三自由度运动过程，建立如图1所示的坐标系。以点O0为北东坐标系原点，建立大地坐标系X0O0Y0，以船舶重心位置G为原点，建立随船坐标系XbG0Yb，其中O0X0轴指向正北，O0Y0轴指向正东。

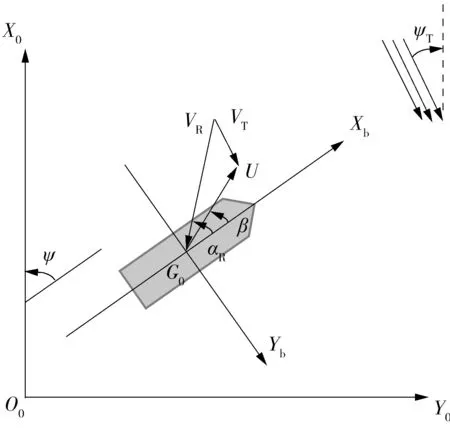
图1 北东坐标系和船体坐标系Fig.1 North-east-down Coordinate & body-coordinate

船舶三自由度非线性运动数学模型可以表示为[22]

(1)

2 ESO-MPC运动控制器设计

所设计的ESO-MPC循迹运动控制器整体控制流程如图2所示。

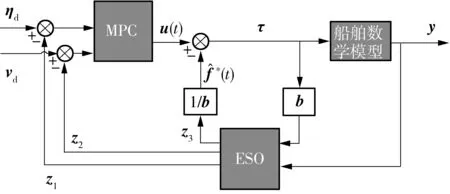
图2 ESO-MPC控制器控制流程图Fig.2 Control flow of ESO-MPC controller

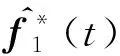
假设1 控制输入η、v对自变量t连续可导有界。

假设2f*(t)满足Rademacher定理，对自变量t连续可导，且有界。

(2)

(3)

(4)

假设4 模型预测控制器中的预测输出与期望输出对自变量t连续可导。

假设5 ESO观测器、MPC控制律以及构造的级联函数连续，满足Lipschitz条件，对自变量t、x1、x2可导。

2.1 ESO设计

结合式(1)，可将船舶三自由度非线性数学模型转化为式(5)所示的状态空间表达形式。

(5)

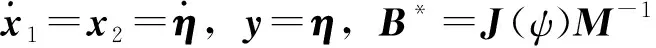
J(ψ)M-1JT(ψ)b(t)-

J(ψ)M-1C(vr)vr-J(ψ)M-1D(vr)vr,

ESO观测器可设计为

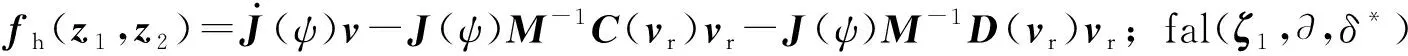
式中，∂和δ*为恒正参数。

2.2 连续时间MPC运动控制器设计

(6)

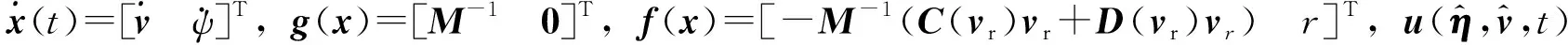
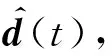
Y(t)2(i+1)×1=y[i]=

(7)

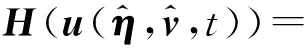
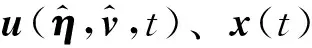
其中，

根据式(7)各阶表达式，θ时刻各阶预测输出y(t+θ)可近似表示为

y(t+θ)=Γ(θ)Y(t)

(8)

其中，Γ(θ)为关于时间的系数矩阵,可表示为

定义被控对象的期望控制输出为W(t)=[w(t)Tw[1](t)T…w[3](t)T]T，其中w(t)T=[udψd]T。

同理将期望输出泰勒展开可得

w(t+θ)=Γ(θ)W(t)

(9)

在预测时域T0内，将各阶预测输出y(t+θ)与期望输出w(t+θ)的差构造为优化目标函数,如式(10)所示：

w(t+θ)]dθ

(10)

结合式(8)与式(9)，式(10)可转化为

(11)

式中，

预测时域T0为调节MPC控制器收敛速度的恒正参数。在合理参数取值范围内，其值越小，收敛速度越快。

令输入偏差矩阵Me=[Me0Me1Me2Me3]T，可表示为

Me=Lf[i]h(x)-w[i](t)

(12)

其中，i=0,1,…,3。

将式(7)代入式(12)得

(13)

(14)

式中，K为控制参数矩阵，取其前两行参数，S(x,t)为控制输入矩阵，可表示为

又令

A=-(LgLfh(x))-1K=[A1A2A3A4]T，

[B1B2B3B4]T。

取S(x,t)、A、B矩阵中与纵向速度相关的第二行及与艏向相关的第三行数值，式(14)可转换为

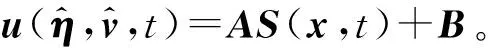
综上，ESO-MPC级联控制器总控制律为

2.3 稳定性分析

将式(5)与式(6)所示的系统相结合，构造如式(15)所示的级联控制系统。

(15)

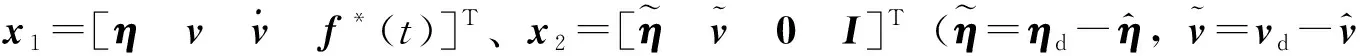
为避免系统F2(t,x2)的输入x2成为奇异矩阵，在矩阵末端设计一个经过系统F2(t,x2)不发生变化且不产生作用的虚拟输入状态量，其值为单位矩阵I；另，级联函数G(t,x1,x2)矩阵末端为0，与系统F2(t,x2)的输入x2相乘为零矩阵，故系统F*(t,x1,x2)不受该虚拟状态量影响。

定理1 若满足假设1-4，t≥0时，F1(t,x1)、F2(t,x2)具有一致全局渐近稳定性，且f1(t,x1)满足如下条件：

证明

(1)F2(t,x2)具有一致全局渐近稳定性

定义恒正控制参数矩阵K=[k0k1]T，将控制律(式(14))代入式(7)得：

(16)

结合输入偏差矩阵Me，式(16)转化为偏差方程形式为

Me2+k1Me1+k0Me0=0

(17)

由于式(17)为2阶Hurwitz多项式，结合非线性广义预测控制稳定性表[23]，系统F2(t,x2)具有一致全局渐近稳定性。

(2)F1(t,x1)具有一致全局渐近稳定性

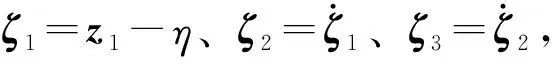
(18)

式中，β1、β2、β3为正增益系数矩阵。

由式(18)可得系数矩阵

令P为满足Lyapunov方程PE+ETP=-I的正定矩阵，定义函数V(ζ)=ζTPζ，W(ζ)=ζTζ，其中I为单位矩阵。

(19)

对函数V(ζ)求导可得

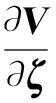
(20)

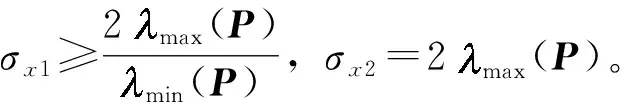
综上所述，系统F1(t,x1)具有一致全局渐近稳定性且E为Hurwitz矩阵，定理1证毕。

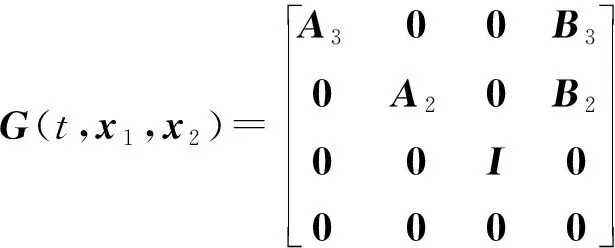
0<‖G(t,x1,x2)‖≤βx1‖x2‖+

(21)

结合定理1，级联系统(式(15))中的x1、x2有界，故βx1可取恒正常数，βx2=0，式(21)可转化为

‖G(t,x1,x2)‖≤βx1‖x2‖

(22)

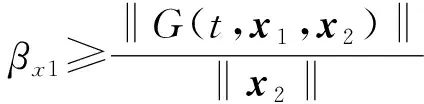
3 仿真实验

3.1 仿真条件设定

文中选取武汉理工大学智能船舶模型WHUT-iship[24]作为研究对象。在风、浪、流和传感器测量噪声等时变多源干扰下，进行ESO-MPC级联控制方法与ADRC、MPC控制方法的仿真对比，以验证所设计控制器的有效性。循迹过程所使用的ILOS引导律见文献[25]，3种控制方法的引导参数设定一致。

ADRC控制形式如下：

连续时间MPC控制形式如下：

3.2 仿真参数设定

仿真环境如表1所示，3种控制器参数如表2所示。

表1 仿真环境参数Table 1 Simulation parameters

ESO-MPC中的参数∂1、∂2、δ*、β1、β2、β3与T0表2中设定一致。

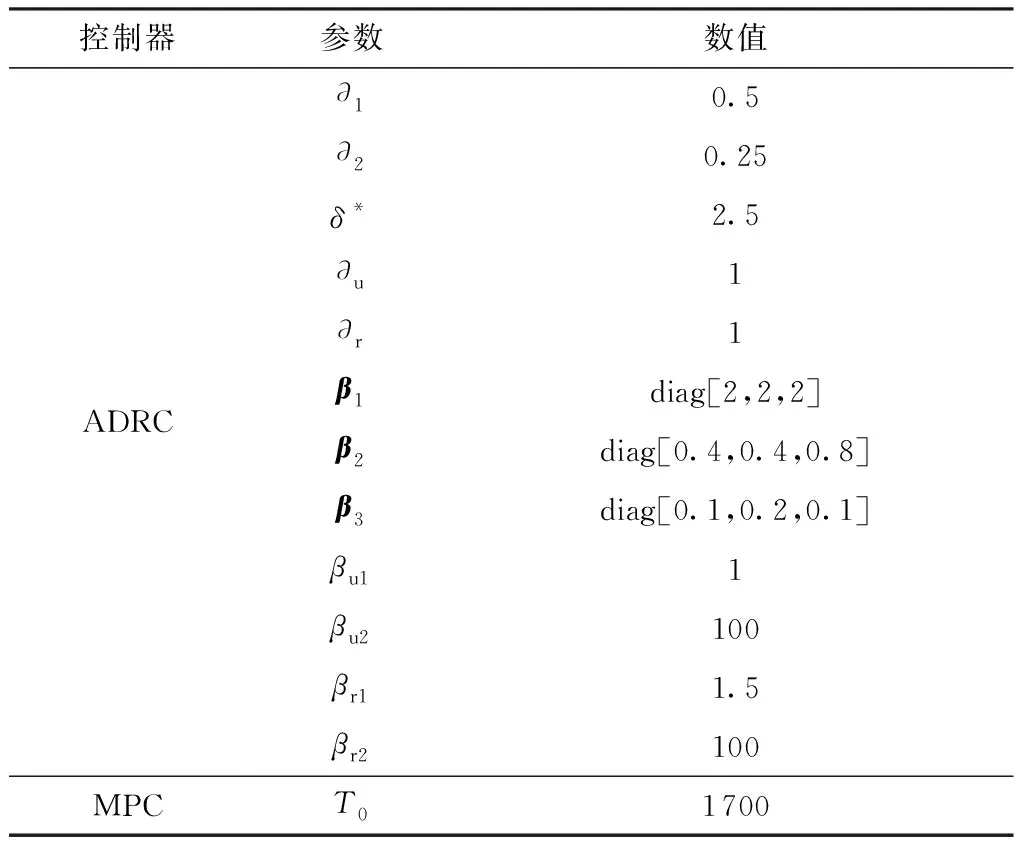
表2 控制器参数Table 2 Controller parameters

3.3 仿真结果与分析

3种控制方法的航行轨迹对比如图3所示。由图3可知，3种控制方法都能沿预设Dubins轨迹附

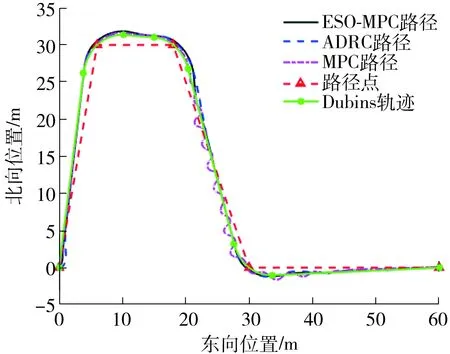
图3 3种控制方法的航行轨迹图Fig.3 Path following results of three control methods

近航行。其中，ESO-MPC与ADRC控制方法的轨迹较平滑，MPC控制方法则有轨迹振荡现象，抵抗外界时变多源干扰能力弱。

图4为3种控制方法的横向偏差对比结果。为进一步量化比较，计算3种控制方法横向偏差的均方误差(Mean Squared Error,MSE)，如表3所示。

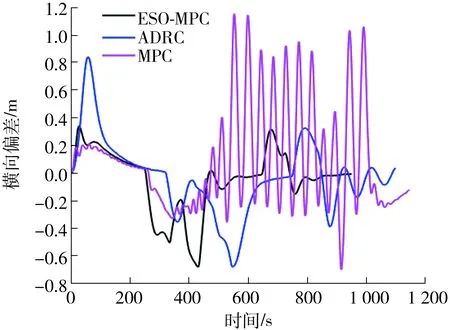
图4 3种控制方法的横向偏差对比Fig.4 Cross-error results of three control methods

由表3可知，ESO-MPC整体横向偏差最小，MPC整体横向偏差最大。在航行过程中ESO-MPC与ADRC横向偏差结果相近，但在航行起始处，ADRC的收敛速度慢于ESO-MPC，其起始阶段的横向偏差较大，且在航行末端具有明显的偏差振荡现象。因此，ESO-MPC级联控制器的鲁棒性最优。

表3 3种控制方法的横向偏差均方误差Table 3 MSE of cross-track error of three control methods

3种控制方法下航行速度及控制力的对比结果如图5、图6所示。由图5可知，在测量噪声干扰下，MPC控制方法下的纵向速度和艏向角速度剧烈抖振，导致其输出的纵向控制力及艏向控制力矩也出现剧烈振荡现象，不利于船舶安全航行且所需航行时间最长，效率最低。采用ESO-MPC与ADRC控制方法速度更平滑，但ESO-MPC控制方法下的纵向速度更平稳且在后续航行过程中始终稳定收敛于期望纵向速度，其航行所需时间最短，效率最高。在艏向角速度图中，采用ADRC方法时，于800 s后出现振荡现象，而采用ESO-MPC控制方法则始终保持平稳。由图6艏向控制力矩图可知，ADRC控制方法在航行转艏处存在控制力矩瞬时突变现象，而经过MPC优化的ESO-MPC控制方法的控制力矩更平滑。由艏向控制力矩子图可知，ESO-MPC控制方法消除了转艏处的瞬时突变，更有利于船舶安全航行作业。

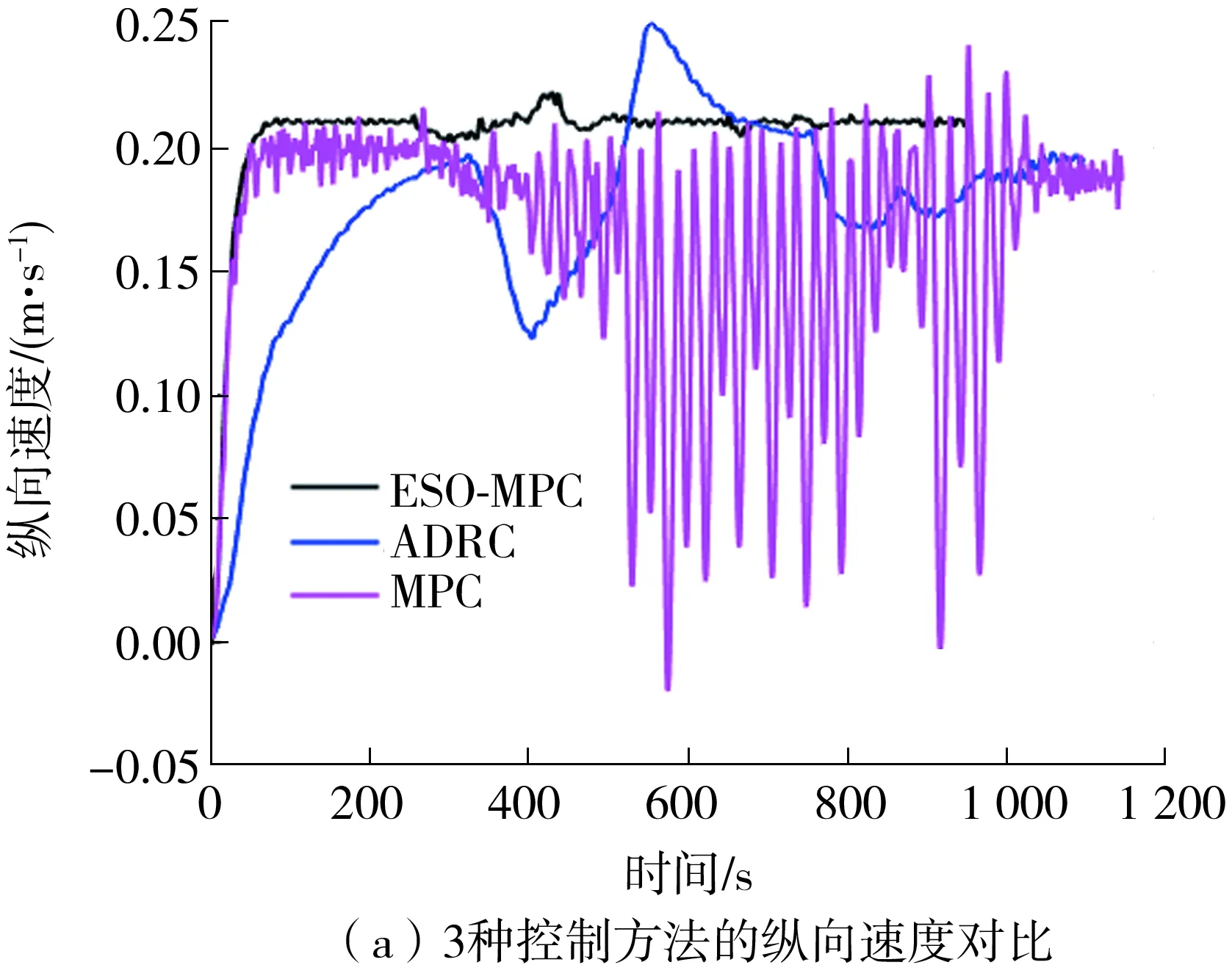
图5 3种控制方法的航行速度对比Fig.5 Speed results of three control methods

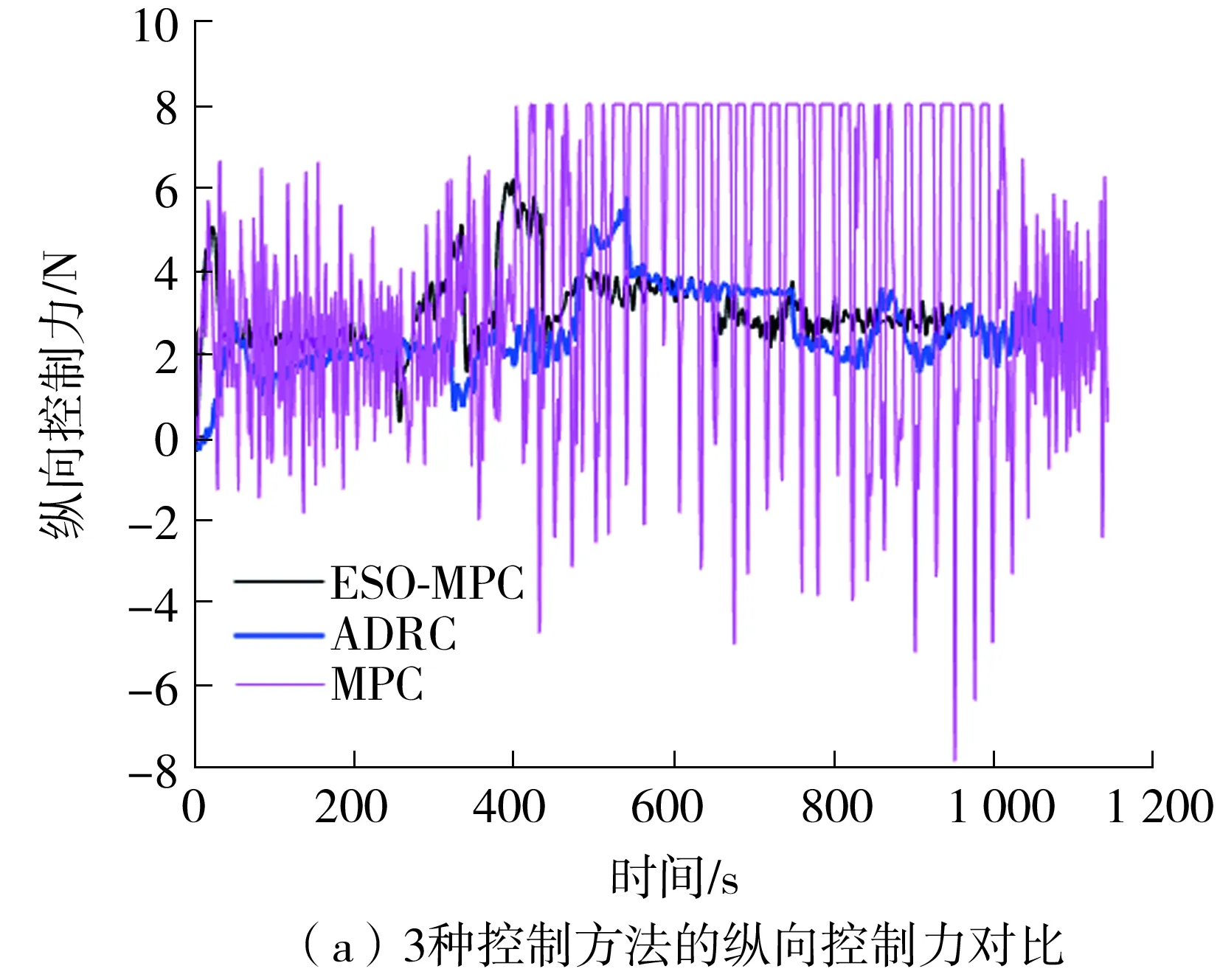
图6 3种控制方法的控制力对比Fig.6 Control force results of three control methods

ESO-MPC控制方法的姿态估计结果及总扰动估计结果如图7、图8所示。

由图7、图8可知，ESO观测器能准确为控制输入端提供低频位置、速度信息，同时能够有效补偿时变多源干扰，为控制器的优化输出提供了保障。综上所述，所设计的ESO-MPC级联控制器考虑了后端执行机构的性能要求，优化了船舶航行所需控制输出，并在时变多源干扰下具有较强的鲁棒性和优越性。

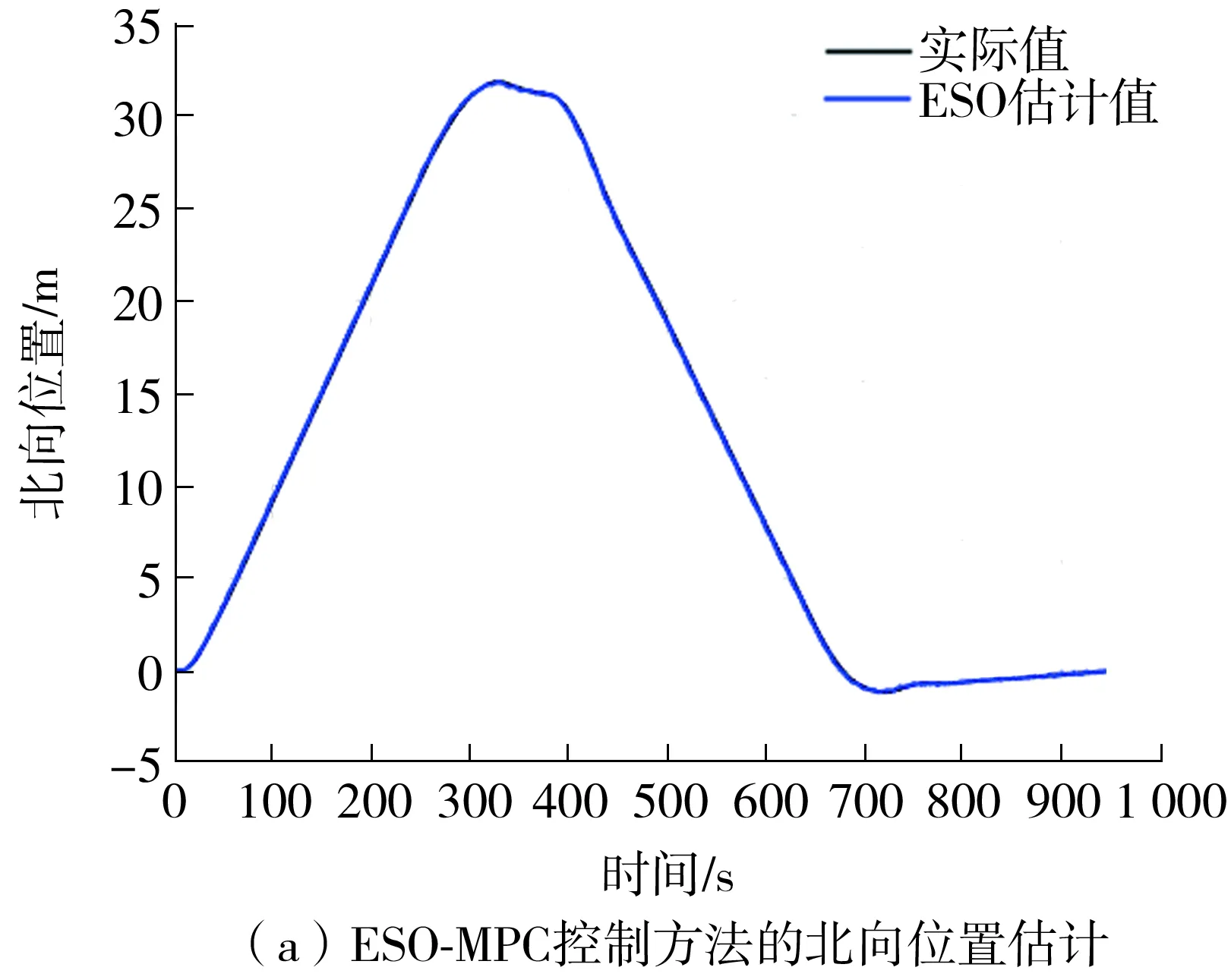
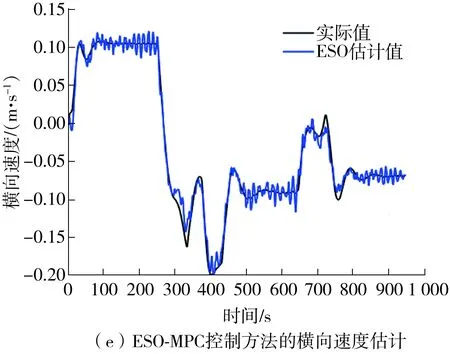
图7 ESO-MPC控制方法的姿态估计Fig.7 Attitude estimation results of ESO-MPC control method

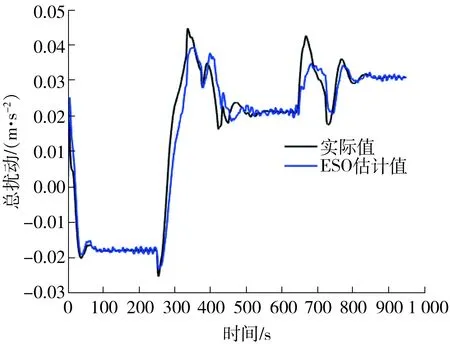
图8 ESO-MPC控制方法的扰动估计Fig.8 Disturbance estimation results of ESO-MPC control method

4 结论

文中针对时变多源干扰下的船舶循迹优化控制进行研究，设计了一种ESO-MPC级联控制器。首先，设计了ESO观测器，有效估计补偿时变多源干扰；其次，以航行控制力为优化目标，设计了MPC控制器以平缓艏向控制力矩中存在的瞬时突变现象，并减小了船舶在时变多源干扰下的航行速度跟踪误差；最终，基于非线性分离式原理证明了该级联控制器的稳定性。仿真结果表明，所设计的ESO-MPC级联控制器平缓了船舶航行转艏处的控制突变现象，并在复杂时变干扰中具有较小的横向偏差；通过与ADRC及MPC方法的仿真对比，进一步验证了ESO-MPC级联控制器的有效性与优越性。