实离散分数Krawtchouk变换及其在数字图像水印中的应用

刘西林，吴永飞，肖翔宇，肖嘉龙，王和锦

太原理工大学大数据学院, 太原 030600

0 引 言

随着互联网的迅速发展，人们与同事、朋友、家人等分享信息变得更加方便，可以便捷地将图像、视频等信息通过网络传播。然而，在享受这种便捷的同时，图像、视频等载体中的个人信息以及分享者的合法权益都会受到威胁。为解决这一问题，数字媒体的安全与保护成为重要的研究课题。通常，数字媒体包括音频，图像和视频；其中，图像是传递信息的主要途径。通过将图像看做2维信号，传统数字信号处理领域的许多技术都可以用来处理图像。

Yap等人(2003)提出了Krawtchouk变换(Krawtchouk transform，KT)，该变换在图像分析领域具有诸多优点，得到广泛研究。根据KT变换矩阵的对称性，Abdulhussain等人(2018)研究了KT的快速计算方法。KT变换的理论研究保证了其在图像识别和图像表示中的广泛应用(Xiao等，2016；Abdulhussain等，2019)。作为传统KT的推广，Liu等人(2017)提出了离散分数阶Krawtchouk变换(discrete fractional KT, DFrKT)，并将DFrKT应用于图像水印。结果显示，DFrKT在图像水印应用中具有较好的表现。本文将Krawtchouk变换推广到实离散分数Krawtchouk变换(real DFrKT, RDFrKT)，并给出了RDFrKT的一些性质。为了验证RDFrKT的实用性，RDFrKT被应用于数字图像水印算法的设计。最后，实验结果表明，基于RDFrKT的水印方案具有较好的水印鲁棒性。

1 相关理论

一维N×N大小的Krawtchouk变换矩阵K(Liu 等，2017)定义为

Kn,x=Kn(x;p,N-1),0≤n,x≤N-1

(1)

式中，Kn(x;p,N-1)是n阶加权Krawtchouk多项式，定义为

(2)

并且

(3)

(4)

(5)

式中，2F表示超几何函数。

矩阵K的特征值分解(Xiao等，2016；肖斌 等，2018)表示为

K=VDVT

(6)

式中，矩阵V表示K的正交特征向量，对角矩阵D表示特征值矩阵，其对角元素为K的特征值。如果N为偶数，D的特征值排列为

(7)

如果N为奇数，则D的特征值排列为

(8)

此外，矩阵K的特征值分解还可以表示为

(9)

式中，d0,d1,…,dN-1是K的特征值，其值为D的主对角元素。v0,v1,…,vN-1是分别对应特征值dk(k=0,1,…,N-1)的K的一组正交特征向量。

根据式(9)，通过对K的特征值取分数阶幂，可以构造离散分数阶Krawtchouk变换(DFrKT)矩阵，α阶DFrKT变换矩阵Kα定义为

(10)

式中，分数阶α取值范围为[0, 1]，v0,v1,…,vN-1是K的一组正交特征向量。那么图像f的(α,β) 阶2维DFrKT可以表示为

Tα,β=KαfKβ

(11)

从式(11)可以发现，DFrKT的变换矩阵Kα和Kβ都是复值矩阵，因此，图像的DFrKT变换将实值图像域变换到了复数域。相应的DFrKT逆变换可表示为

f=K-αTα,βK-β

(12)

从式(12)可以发现，如果变换系数Tα,β被误差干扰，重构图像f将是复值函数。如果使用被误差干扰的扰动系数来重建图像，得到的图像域是个复数域，需要额外的存储空间来储存重建图像。

2 实离散分数阶Krawtchouk变换

2.1 RDFrKT的定义

根据DFrKT的定义可知，DFrKT变换矩阵的构造是通过对Krawtchouk变换矩阵K进行特征值分解后，对特征值取分数次幂得到的。为了构造变换域为实数的DFrFT变换来处理实值信号，Hsue和 Chang(2015)给出了一种根据变换矩阵的特征值分解来构造实离散分数阶Fourier变换的方法。本文将该方法推广到RDFrKT的定义。

(13)

(14)

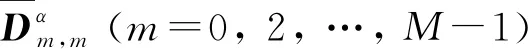
(15)

(16)

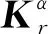
(17)

根据式(17)，2维逆RDFrKT可以定义为

(18)

2.2 RDFrKT变换矩阵的性质

通常而言，构造的分数阶变换矩阵应满足3个条件：一致性、阶数可加性和幺正性。对所提出的RDFrKT而言，传统的KT变换是RDFrKT的一个特例，一致性条件满足；并且它具有阶数可加性和幺正性。RDFrKT的性质解释如下：

性质3：阶数可加性，即

(19)

证明：由式(13)可得

(20)

(21)

即证。

性质4：幺正性，即

(22)

性质4的证明可通过使β=-α和使用性质1来实现。

3 在图像水印中的应用

相对于复变换域，信号的实变换域具有在计算机中存储时占用空间少、在数字通信信道占用带宽少的优点，实值变换已用于图像加密(Kang等，2019；Lang，2012；Zhou等，2012)和图像分类(Zhang等，2018)等图像处理应用中。作为RDFrKT的一个应用，基于所提出的RDFrKT，本文提出一种结合RDFrKT和奇异值分解(singular value decomposition, SVD)数字图像水印方案。基于SVD的水印方案一般通过两种方式嵌入水印：通过修改奇异值嵌入水印(Mohammad等，2008；Run等，2012；Pei和Liu，2008；Guo和Prasetyo，2014)和将水印嵌入奇异向量(Jia，2014；Hu等，2020)。而且，为了增强水印的鲁棒性，可以将水印嵌入到图像DCT(discrete cosine transform)变换域的SVD中(Tian等，2020；Singh和Singh，2017)。实值变换将实值的图像域映射到实值的变换域，对实值的变换域处理后逆变换域仍然是实值。这样，对图像的实变换域修改后逆变换得到的仍然是实的图像域。因此，在图像的实变换域嵌入水印信息是理想的选择。

本文通过图像RDFrKT的变换域嵌入二值水印信息，将水印信息嵌入到RDFrKT变换域的奇异值分解后的奇异向量中。水印方案分为两个阶段：水印嵌入阶段和水印提取阶段。图1和图2分别直观地给出了水印的嵌入和提取流程。

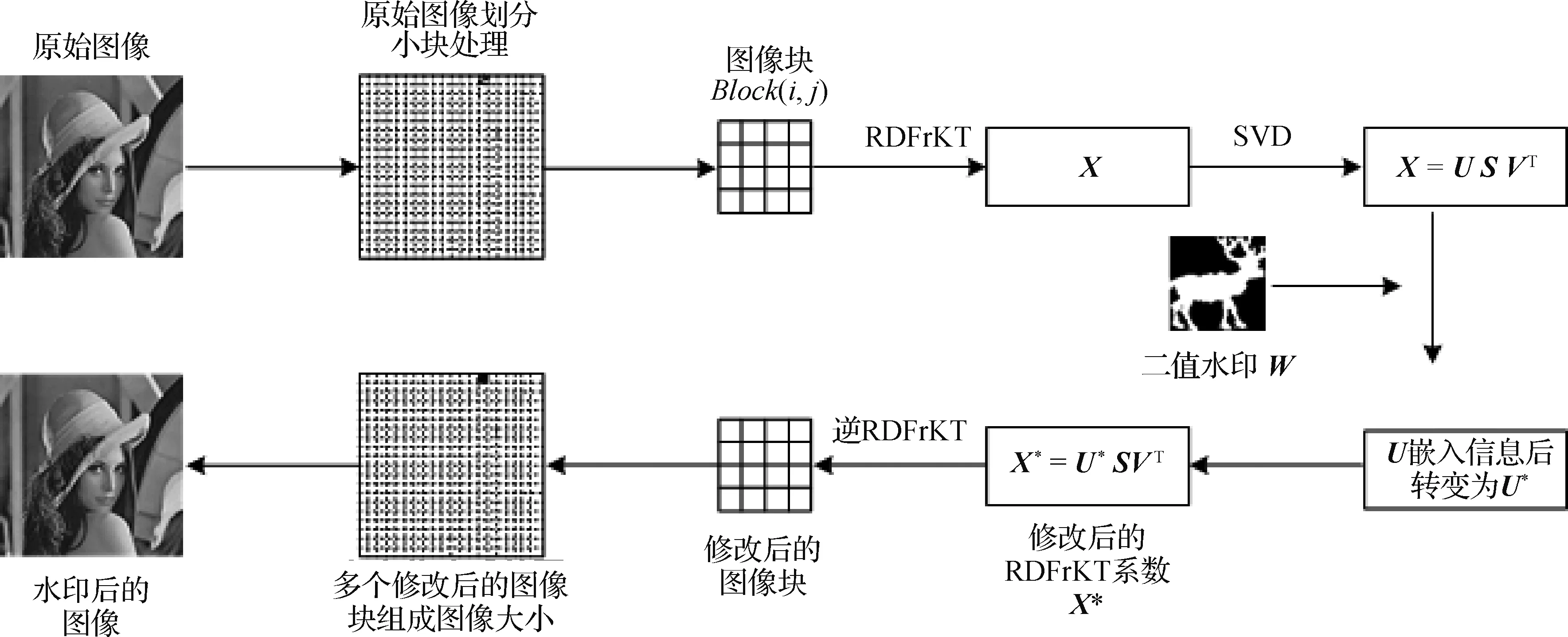
图1 水印嵌入流程Fig.1 The proposed watermark embedding procedure

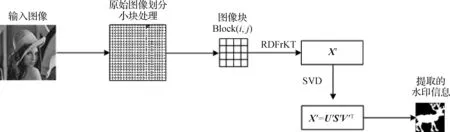
图2 水印提取流程Fig.2 The proposed watermark extraction procedure

3.1 水印嵌入流程

考虑N×N大小的原始灰度图像A和m×m大小的水印二值图像W。水印的嵌入流程包括以下几个步骤：

1)将原始图像A分成4×4大小的不重叠的图像块。

2)为了加强水印的安全性，随机选取m2(m≤N/4) 个图像块。图像块的选取位置可以看做秘钥KEY1。

3)对每个块执行RDFrKT，得到变换域系数X。

4)对每个块的RDFrKT系数执行SVD分解，即

X=USVT

(23)

式中,U为X的左奇异向量矩阵，V为右奇异向量矩阵，S为奇异值矩阵。

5)通过修改左奇异向量矩阵第1个奇异向量的第2个元素u21和第3个元素u31的差值来嵌入1 bit水印w。设g=u21-u31，水印块使用以下扰动调制的方法(Hu等，2020)通过修改g来嵌入水印，即

(24)

式中，g*是对g嵌入水印后的值，γ21和γ22表示为

(25)

(26)

(27)

式中，max()和min()分别表示函数的最大值和最小值。式(24)—(27)给出的参数ρ,η,D，δ=0.5D,ψ=D,ρ=1.5D,η=2D，调整量化步长D来平衡水印的鲁棒性和不可见性。

6)在修改g嵌入水印之后，可以得到修改后的奇异向量元素u21和u31为

(28)

7)得到修改后的RDFrKT系数X*为

X*=U*SVT

(29)

式中，U*为嵌入水印后图像块的左奇异向量矩阵。

8)对每个块的修改后的RDFrKT系数X*执行逆RDFrKT来获得加水印后的图像A*。

3.2 水印提取流程

假如接收到一幅图像A′，必须拥有秘钥KEY1，才能正确地提取出水印信息。详细的水印提取步骤如下：

1)将接收到的图像A′分成4×4大小的不重叠的图像块。

2)使用KEY1定位正确水印的图像块。

3)对每个块Block(i,j)进行RDFrKT来获得变换域系数X′，接着对X′进行SVD分解，得到

X′=U′S′V′T

(30)

式中，U′为X′的左奇异向量矩阵，V′为右奇异向量矩阵，S′为特征值矩阵。

4)从左奇异向量矩阵的第2和第3个元素u′21和u′31之间的差g′中提取水印比特，即

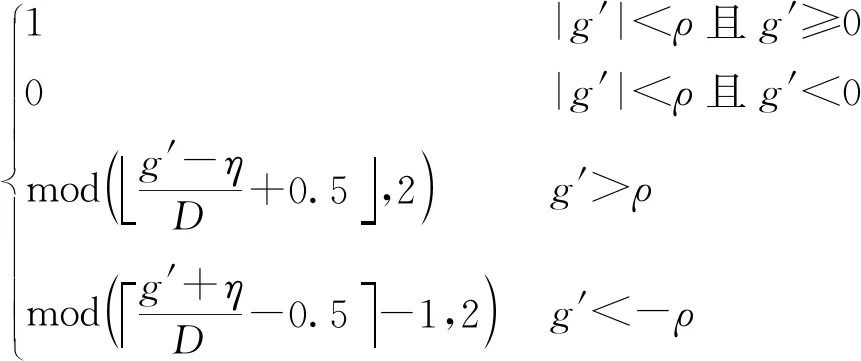
(31)

式中，mod(·,2)表示取模运算，w′为一个图像块提取的1 bit水印。

最后，组合所有图像块提取的水印信息可以用来确定图像的所有权或验证版权。

4 实验结果及分析

为了验证提出的基于RDFrKT的水印算法的有效性，实验采用了Granada大学计算机视觉组的图像数据库(http://decsai.ugr.es/cvg/dbimagenes/)中的96幅大小为256×256像素的灰度图像为测试图像。采用MPEG-7二值图像形状数据库(http://imageprocessingplace.com/root_files_V3/image_databases.htm)中的64×64像素“Deer”二值图像为水印。图3 给出了几种测试图像和水印图像实例。实验中，水印图像嵌入到测试图像后生成嵌入水印的载体图像。然后，载体图像经过滤波、噪声等图像攻击后，测试从受攻击的载体图像提取水印信息的有效性，从而验证所提算法的有效性。为了验证所提水印算法的鲁棒性能，将本文方法与基于DCT、KT 的方法和基于Hu的 SVD方法(Hu等，2020)进行了比较。同时，为了保证比较的公平性，本文水印算法同时考虑了修改奇异向量时产生的移位、符号矫正、正交恢复等预处理操作(Hu等，2020)。

为了度量水印在载体图像中的不可见性，实验采用了峰值信噪比(peak signal to noise ratio，PSNR)来衡量，其定义为(Run等，2012)

(32)

式中，MSE表示水印图像A*和原始图像A*之间的均方误差，定义为

(33)

为了保证嵌入水印后载体图像的视觉质量，实验对水印参数进行了调整，使测试图像的平均PSNR为37.58 dB。然后选择量化步长D=0.025。根据实验测试，为了得到鲁棒的水印算法，RDFrKT变换中分数阶阶数的选取为α=0.6，β=0.4。水印鲁棒性用误码率(bit error rate，BER)来衡量，定义为(Tian等，2020)

(34)

式中，W*是提取的水印图像，W是尺寸为l×l的原始二值水印。

首先以Lena图像作为原始图像，将“Deer”水印嵌入到原始图像中。然后，嵌入水印的载体图像受到各种类型的水印攻击，如中值滤波、均值滤波、高斯滤波、JPEG压缩、图像缩放、椒盐噪声和高斯噪声。然后从受攻击后的载体图像中提取水印。图4给出了一些提取的水印及其在不同攻击情况下对应的BER值。可以看出，在大多数攻击情况下，基于RDFrKT方法提取的水印比其他方法具有更低的BER值。这表明基于RDFrKT的方法具有更好的性能。

图3 测试图像数据库和二值水印图像的若干样本Fig.3 Some samples of the test image database and binary watermark image

中值滤波3×3均值滤波3×3高斯滤波标准差0.5JPEG品质因数 90缩放参数0.9椒盐噪声密度0.001高斯噪声密度0.0010.188 70.253 20.025 600.179 90.010 70.503 2(a)本文0.402 80.425 80.066 90.006 30.205 60.006 80.476 8(b)DCT0.382 60.446 80.094 50.005 90.243 40.003 40.510 5(c)KT0.494 60.516 10.034 90.008 50.294 20.002 20.481 9(d)Hu等人(2020)

图像库中的96幅图像为测试图像，将水印分别嵌入其中得到嵌入水印的载体图像。然后，所有的载体图像分别在中值滤波、均值滤波、高斯滤波、JPEG压缩、图像缩放、椒盐噪声和高斯噪声等各种水印攻击后提取嵌入信息。统计了所有测试图像的平均BER值来验证本文所提算法的鲁棒性能。图5给出了各种类型攻击下，平均BER值随攻击强度的变化情况，并将本文算法与基于DCT的水印算法、基于KT的水印算法、Hu等人(2020) SVD水印算法进行了比较。结果表明，基于DFrKT 的水印算法在大多数情况下都具有更好的鲁棒性，特别是对中值滤波、均值滤波、高斯滤波和 JPEG压缩这几类图像攻击。

5 结 论

本文提出了实离散分数Krawtchouk变换(RDFrKT)。与现有的离散分数Krawtchouk变换 (DFrKT)相比，RDFrKT可以将实数值的灰度图像域变换到实数值的变换域。于是，RDFrKT变换域具有和图像相同的存储空间；并且，图像的RDFrKT变换域进行处理后进行反变换，得到的图像空间仍然是实数域。因此，RDFrKT不仅保持了传统Krawtchouk变换是实变换的特点，并且具有可随分数阶阶数调整的变换域，在图像处理中具有广泛的应用前景。作为RDFrKT的一个应用，该变换已用于数字图像水印算法的设计。结果表明，基于RDFrKT变换的水印方案，对图像中值滤波、均值滤波、高斯滤波、JPEG压缩和缩放等多种信号处理攻击具有较好的鲁棒性。本文设计的水印算法结合了RDFrKT和SVD，在图像的奇异向量中嵌入了水印信息。在未来的工作中，RDFrKT可以与SVD结合，将水印信息嵌入到奇异值来探索水印算法的性能。此外，所提出的变换有望应用于图像加密和其他水印应用中。一种思路是可以将辛怡等人(2008)的实分数阶Fourier变换域图像加密算法扩展到RDFrKT变换域。

图5 各种攻击类型下平均BER值随攻击强度的变换情况Fig.5 Average BER value variation with attack parameter changes of different attack situations((a) median filter; (b) average filter; (c) Gaussian filter; (d) JPEG compression; (e) image recalling; (f) salt and peppers noise; (g) Gaussian noise)