Cr在α-Fe(C)中对C扩散影响的第一性原理研究

王辉，苏福永，刘文丽，温治

(北京科技大学能源与环境工程学院，北京，100083)

碳是铁基合金中最常见的间隙原子之一，通过形成碳化物[1]、晶界碳偏析[2]、硬化和脆化效应[3]等，可显著提高钢的强度和硬度[4]。碳在铁中的分布和扩散可以影响钢中许多过程，如碳化物沉淀、马氏体老化和铁素体转变等[5]。从微观上研究铁中碳原子的扩散行为，有利于更好地解释碳原子对铁合金性能的影响规律和机理。只有明确碳原子在铁晶体内的扩散路径，才能通过改进工艺设计和合金成分来减弱或增加碳原子的吸附和扩散能力，改善金属性能。

为改善钢的性能，常在铁基合金添加元素。例如，添加Cr 元素可使钢材具有更好淬透性，增加其碳化物的稳定性，延长钢材的使用寿命。封辉等[6]发现随着Cr元素质量分数增加，低合金高强耐候钢的强度上升，塑性下降。Fe-Cr 多层体系还因其巨磁阻效应而广泛应用于存储器件中[7−8]。侯瑞东等[9]通过实验研究发现，900～950 ℃温度条件下，随Cr 质量分数增加，钢的抗氧化性增强。然而，Cr 元素的加入给铁基合金带来一系列优良性质的同时也将与其中的其他原子发生相互作用，例如它会与碳原子之间产生化学或电子效应[4]，从而影响钢中碳的行为，如碳溶解度极限[10]，显微偏析[11]，扩散[12]和碳化物沉淀[13]等。

迄今为止，基于密度泛函理论(DFT)的第一性原理可以准确评估原子相互作用，是研究一些基本原子现象的有力工具。JIANG等[14]采用该方法计算了C 在α-Fe 和γ-Fe 中的溶解和扩散，发现α-Fe中2 个八面体位置之间的碳扩散的最小能量路径(MEP)具有0.86 eV 的势垒，与实验值0.87 eV 接近。HERSCHBERG 等[15]计算在不同局部化学环境中1组C扩散的结合能和迁移能垒，采用动力学蒙特卡罗方法模拟Fe-Cr合金中C的扩散特征，发现在Fe-Cr合金中C扩散的平均迁移势垒随着Cr浓度增加而逐渐增加。孙兴广等[16]对Fe-Cr-Ni合金中点缺陷相互作用能的计算表明，相邻空位表现出相互吸引作用，会促进孔洞形成。VON APPEN 等[17]利用密度泛函理论研究了奥氏体Fe-Mn 合金中的氢间隙，发现八面体H的间隙位置更倾向于含Mn原子的局部环境而不是Fe原子。SANDERG等[18]采用第一性原理密度泛函理论计算了体心立方Fe 和Cr中C溶液焓和扩散活化焓，2个体系中计算得到的焓与实验焓的偏差均小于0.05 eV。SIMONOVIC等[19]计算了间隙碳与取代硅的相互作用以及这种相互作用对体心立方铁中碳的扩散的影响，并预测计算扩散的活化能和扩散前因子。

目前，虽然学者们研究了α-Fe 中的碳扩散特征，但是都没有详细解释α-Fe 中Cr 原子和C 原子的相互作用和铬对碳扩散影响。因此，本文首先基于第一性原理方法计算了α-Fe 中Cr 原子和C 原子的相互作用能；其次，通过态密度计算分析了各原子之间的成键情况以及其对结构稳定性的影响；最后，用攀升图像微扰弹性带(CI-NEB)方法对α-Fe 中C 原子的扩散特征进行了分析，同时还研究了Cr原子对α-Fe中C原子的扩散的影响。

1 计算方法与结构模型

本文中第一性原理计算基于自旋极化密度泛函理论[20−21]，在维也纳大学开发的Vienna Ab initio simulation package(VASP)[22−23]软件包中计算。利用VASP 求解具有周期性边界条件和平面波基组的Kohn-Sham 方程。离子和电子的相互作用采用投影缀加波方法(PAW)[24−25]计算，电子交换关联泛函采用广义梯度近似GGA[26]下的PBE 泛函形式。通过收敛测试，平面波截断能取450 eV，使能量收敛到每个原子0.1 meV 以内。布里渊区积分采用Г点为中心的Monhkorst-Pack方法产生的k网格点方法，在2×2×2(16 个原子)，3×3×3(54 个原子)和4×4×4(128 个原子)的α-Fe 超胞的计算中分别采用选取8×8×8，6×6×6 和4×4×4 的k 网格，使原子所受力小于0.2 eV/nm。

本文采用HENKELMAN等[27−28]开发的过渡态包(VTST)中的攀升图像微扰弹性带(climbing image nudged elastic band，CI-NEB)方法计算C 原子扩散过程中的能量壁垒，这种方法也提供了一种寻找最小能量路径(MEP)的方法。计算过程中图像弛豫的收敛标准为作用于原子上的力小于0.1 eV/nm。

C原子的原子半径较小，通常认为在α-Fe中占据间隙位置。为了确定C原子占据的是四面体位置还是八面体位置，本文计算了C 原子在α-Fe 中的溶解焓ΔHs，其表达式为

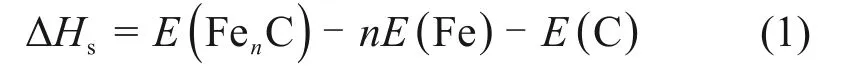
式中：E(FenC)为包含n个Fe原子和1个C原子的α-Fe 晶胞的能量，eV；nE(Fe)为包含n个Fe 原子的α-Fe 晶胞的能量，eV；E(C)为单个石墨原子的能量，eV。为了能更好消除误差，E(FenC)和nE(Fe)这2 项能量采用相同的参数(截断能及K 点等)进行计算。石墨分子采用8×8×4的网格，450 eV的截断能进行计算。

当α-Fe 中溶质原子X和Y原子之间相距Rs时，有效相互作用能表达式为[19]

式中：s 为特定相邻位置的壳层；E(FenXY,Rs)为溶质原子X和Y之间相距Rs时体系的能量，eV；因为计算所采用的晶胞尺寸有限且计算时周期性的边界条件，所以某些相对位置的计算中溶质原子X和Y之间会发生多次相互作用，本文用m来表示这种情况。ΔE(X)和ΔE(Y)分别为单个溶质原子X和Y的能量，eV。其表达式为[19]：

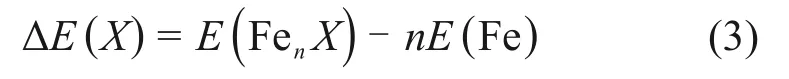
式中：E(FenX)为包含n个铁原子和一个溶质原子X的α-Fe晶胞的能量。

2 计算结果与讨论

2.1 α-Fe（C）-Cr体系结构分析

基于密度泛函理论第一性原理，分别采用超软赝势(OTFG ultrasoft)和投影缀加波(PAW)方法对3×3×3的α-Fe超胞进行了优化和能量计算，计算得到的纯铁磁性α-Fe 的晶格边长均为0.283 nm，每个Fe 原子的磁矩分别为2.18μB和2.21μB(μB=9.272 6×10−24A·m2)，如表1所示。这与之前学者计算得到的结果相近，但投影缀加波方法计算得到的结果和实验结果符合更好，故本文的计算均采用投影缀加波方法。

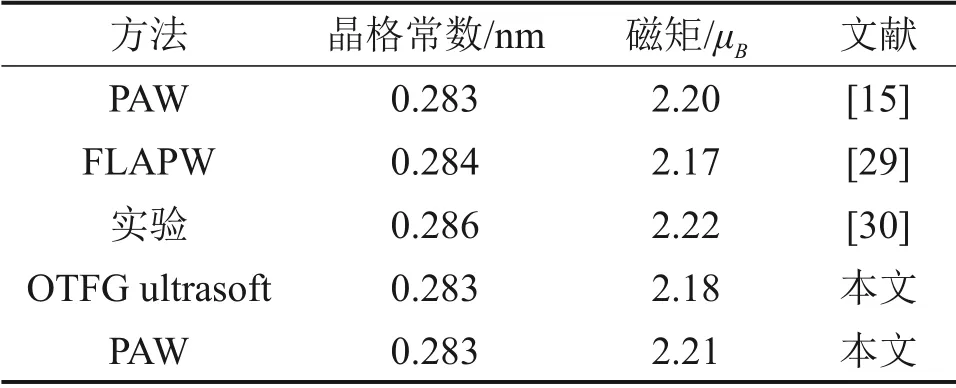
表1 UUSP和PAW计算结果与文献结果的对比Table 1 Comparison of UUSP and PAW calculation results with literature results

由于Cr原子的半径与Fe原子的半径相似，当Cr原子加入到α-Fe中时，会直接替代Fe原子的位置。α-Fe 中Fe 的占位有2 种，分别为体心位置和顶角位置。所以，为了确定Cr 原子在α-Fe 中的占位，本文分别计算了Cr 原子在2×2×2 的α-Fe 晶胞中占据2种不同位置时晶胞的体积和总能量，然后计算了Cr 原子替代Fe 原子后体系的体积变化率，体积变化率ε计算公式如下：

式中：V为Fe15Cr 晶胞的体积；V0为Fe16晶胞的体积。计算结果如表2所示。

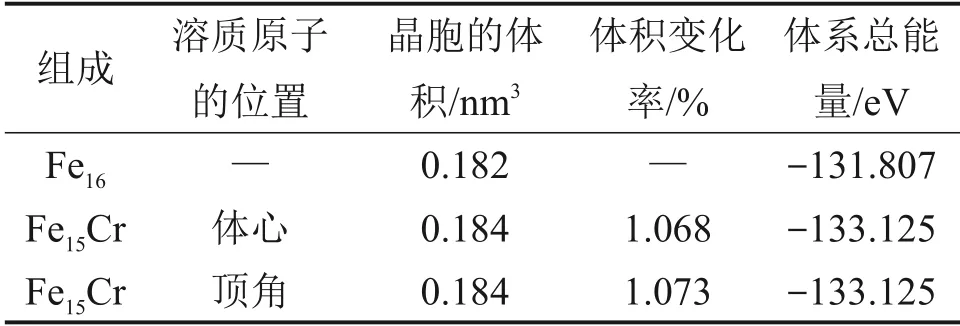
表2 Cr原子占位分析Table 2 Cr atomic occupancy analysis

由表2可见，Cr 原子加入到α-Fe 中引起了晶格畸变，Cr 原子占据体心位置时的体积变化率略小于占据顶角位置时的体积变化率，但差别不大，说明Cr 原子在α-Fe 中可能是随机占位。此外，Cr原子占据2种位置时体系总能量没有差别，这也可以验证上述观点。由于Cr 原子占据体心位置时的体积变化率略小于占据顶角位置时的体积变化率，本文后续的工作都按Cr 原子占据体心位置来进行计算。通过对Fe(Cr)体系的计算，Cr 原子在α-Fe中表现为反铁磁性，后续计算中Fe 原子按照铁磁性，Cr原子按照反铁磁性设置。

C原子的原子半径较小，通常认为在α-Fe中占据间隙位置。为了确定C原子的具体占位情况，本文分别在八面体和四面体间隙位置插入了C原子，并计算了C原子在这2种位置的溶解焓，结果如表3所示。由表3可见，C 原子占据八面体位置时体系的总能量和溶解焓相比于占据四面体位置时的低，因此，C在α-Fe中优先占据八面体位置，这与DUNLOP等[13]的计算结果一致。

表3 C原子占位分析Table 3 C atomic occupancy analysis

Cr 元素给铁基合金带来一系列优良性质可能与基体的键合作用有关。建立了Fe15CrC的α-Fe-Cr合金体系，并分析了其电子结构，计算了α-Fe-Cr合金体中各原子的分态密度，分析键合作用，结果如图1所示。

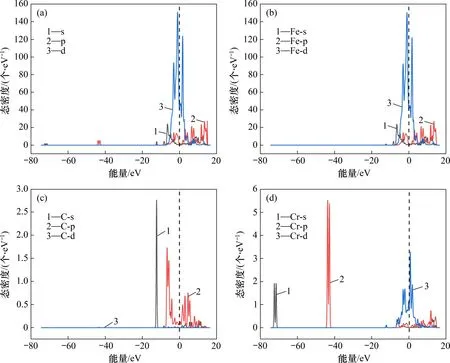
图1 α-Fe(C)-Cr合金体系的态密度图(DOS)和分态密度图(PDOS)Fig.1 Density of states(DOS)and partial density of states(PDOS)of α-Fe(C)-Cr alloy systems

从图1可见：α-Fe-Cr 合金体系成键电子主要分布在−75.0～−71.9，−45.0～−42.0，−12.5～−12.0 和−8.0～15.0 eV 等4 个区间，而从图1中费米能级处有很明显的成键峰的是Fe 3d 轨道和Cr 3d 轨道，这2 条轨道的杂化导致DOS 图费米能级处出现了尖锐波峰，而C在此处的态密度几乎为0，因此Fe和Cr 在此处强烈成键，C 原子虽然在−12.5～−12.0 eV 区间内提供成键电子，但Fe 和Cr 在这2个区间的态密度却很小，因此，在α-Fe(C)-Cr合金中，3 种原子都提供成键电子，但Fe 和Cr 是成键的主要因素。

态密度能判断原子间成键情况，也能够具体分析成键的轨道，但不能对成键进行量化描述，因此，为更直观地揭示合金元素Cr 与Fe，C 原子间的键合强度，从电子结构方面进一步量化成键强度，计算了α-Fe(C)-Cr 的Bader 电荷布居，结果如表4所示。

表4 α-Fe(C)-Cr的barder电荷布居Table 4 Barder charge population of α-Fe(C)-Cr

从表4可见：在α-Fe(C)-Cr晶体中Cr原子的电荷数为11.495 9，小于纯铬晶体中电荷数12，说明Cr原子加入到α-Fe(C)体系中后失电子，Fe原子一部分得到电子，一部分失去电子，但总体来说表现为失电子，只有C原子的电荷数增加了1.146 9，这说明Cr原子加入α-Fe基体内后，Cr原子和Fe原子失去电子，C得到电子，三者之间形成离子键的相互作用，导致铁素体晶胞得到强化。

2.2 α-Fe中Cr与C的相互作用

为了进一步分析Cr原子加入α-Fe(C)体系后对C原子的影响，本节在4×4×4的α-Fe晶胞中建立了Cr 原子和不同近邻位置C 原子的结构示意图，如图2所示。图2给出了2 个5 近邻位置的位置，分别用5 和5′表示，图2中Cr-C5 之间上没有其他原子，而Cr-C5'之间有1个Fe原子。

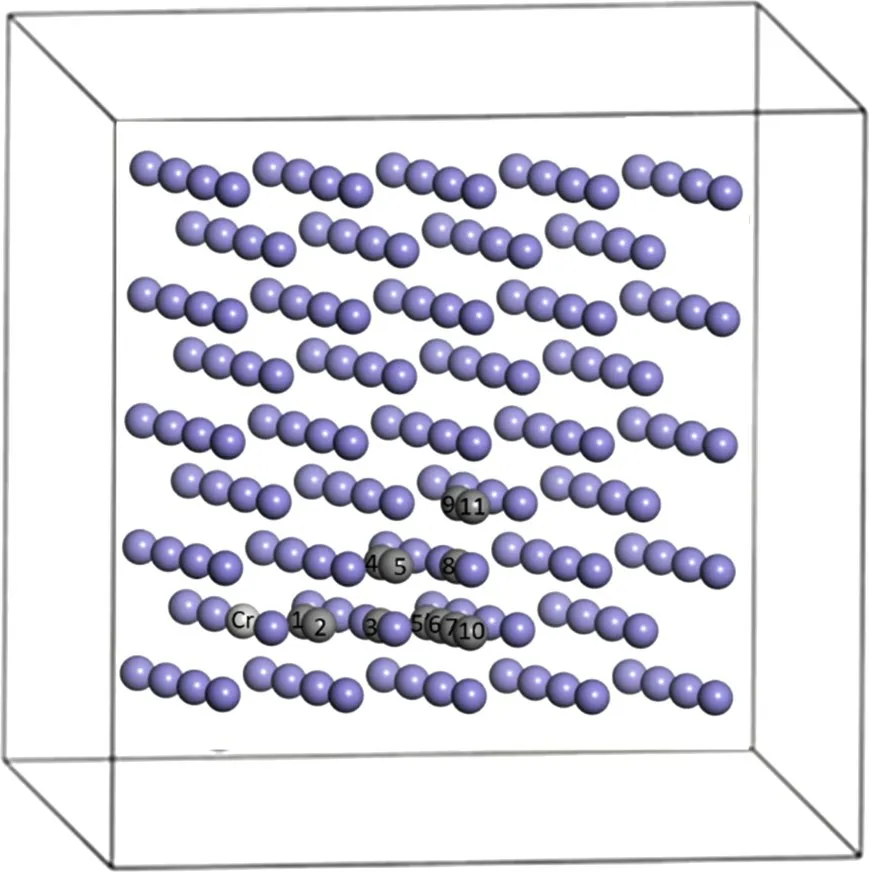
图2 α-Fe中Cr原子和不同近邻位置C原子的结构示意图Fig.2 Schematic diagram of Cr atom structure in α-Fe crystal and C atom in its different neighboring positions

对含有Cr 原子且在其第一近邻八面体位置加入C原子的α-Fe晶体进行结构优化。图3所示为结构优化前后α-Fe 晶体中的Cr 原子和C 原子所在的<010>方向的切面上的结构图，其中，蓝色的圆球代表Fe原子。从图3可见，与结构优化之前相比，结构优化后Cr 原子沿<010>方向向左边移动，Cr原子和C 原子之间的距离由0.142 nm 增加到0.182 nm，这说明Cr 原子与在其第一近邻八面体位置的C原子存在排斥力。

图3 α-Fe-Cr-C晶胞结构优化前后结构变化图Fig.3 Structure change diagram of α-Fe-Cr-C cell structure before and after optimization

本文分别在Cr 原子的不同近邻位置加入C 原子进行结构优化，分析结构优化前后Cr 原子和C原子之间的距离变化情况，利用式(2)计算它们之间的相互作用能，结果如表5所示。

为了更直观描述Cr 原子C 原子之间相互作用能随距离的变化，计算所得的Cr 原子与不同近邻位置C原子的相互作用能，如图4所示。由表5及图4可知，Cr 原子和C 原子之间一直存在排斥力。随着距离增加，Cr 原子和C 原子之间的相互作用能逐渐降低，且在距离超过1.75aα-Fe时逐渐趋于0，其中，aα-Fe为α-Fe 晶胞的晶格常数。对于5 近邻位置和5′近邻位置构型，两者相互作用能的不同是因为图中Cr-C5之间上没有其他原子，而Cr-C5′之间有1个Fe原子。

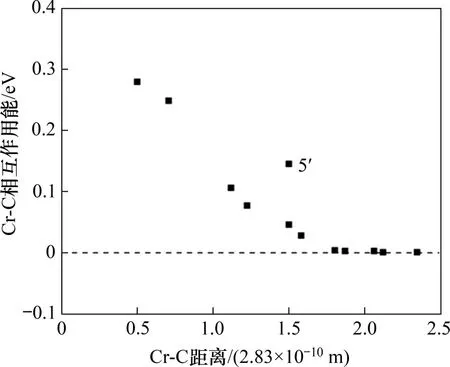
图4 α-Fe中间隙Cr原子与八面体位置C原子间的相互作用能随距离的变化Fig.4 Interaction energy with distance between interstitial Cr atoms and octahedron position C atoms in α-Fe

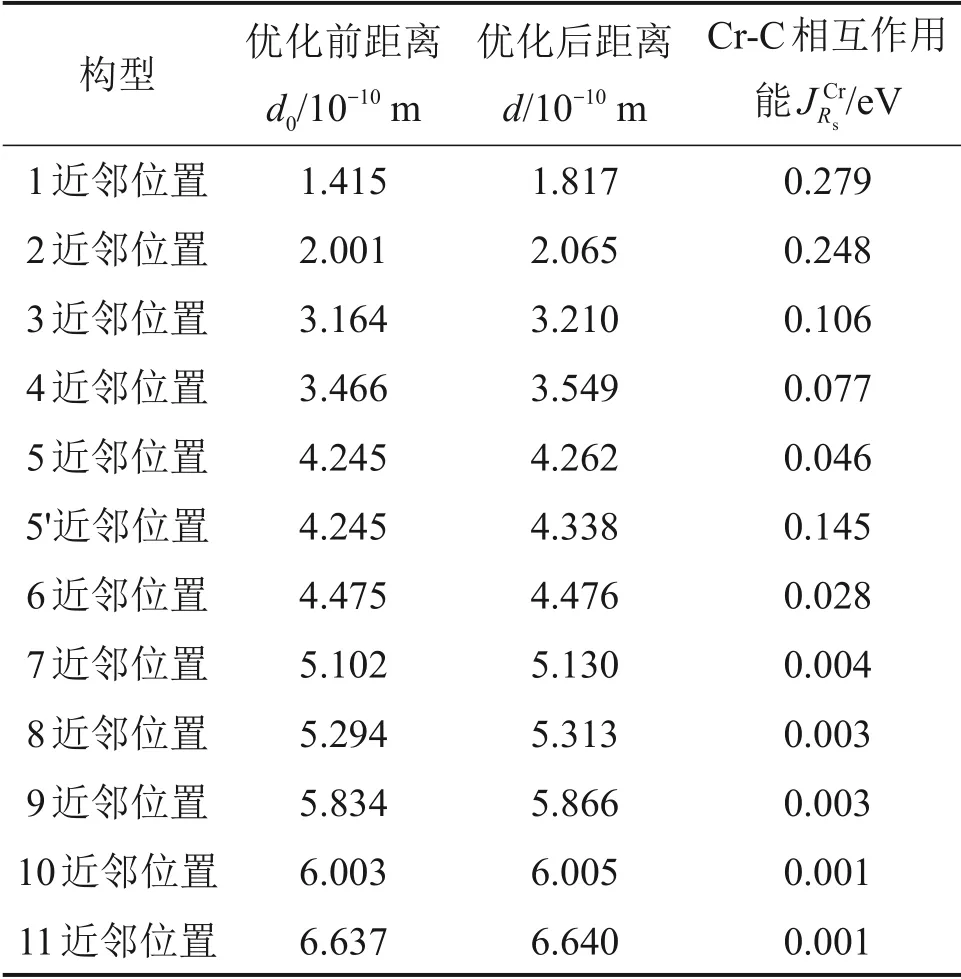
表5 结构优化前后Cr原子与C原子之间间距的变化及相互作用能Table 5 Interaction and distance change between Cr and C atoms before and after structural optimization

2.3 Cr对C在α-Fe中扩散的影响

α-Fe 中Cr 原子与C 原子的相互作用会影响C原子的扩散，但具体的影响程度还不太清楚。

首先，建立了3×3×3 的Fe54C 模型，利用CI-NEB 方法计算了C 原子在2 个相邻的八面体位置间的扩散。扩散过程能量变化如图5所示。从图5可知：C原子位于八面体位置时，体系能量最低。C原子扩散到四面体位置时，体系能量最高，说明四面体位置是C原子在2个相邻八面体位置之间扩散过程中的过渡态位置。计算得到扩散激活能为0.89 eV，与DOMAIN 等[31−32]DFT 模拟结果和实验结果符合很好，验证了本文计算扩散激活能方法的准确性。

图5 3×3×3晶胞计算得到的最小能量路径Fig.5 Minimum energy path calculated from 3×3×3 unit cells

然后，分别计算C 原子在Fe54C 和Fe53CrC 这2种模型中向其第一、第二近邻位置扩散的路径和扩散激活能，结果如图6所示。从图6可见：α-Fe(C)体系和α-Fe(C)-Cr体系中C原子在向第一近邻位置扩散的方式为O-T-O(O代表八面体位置，T代表四面体位置)，向第二近邻位置扩散方式为O-T-O1-T-O2。2 种体系中C 原子在向第一及第二近邻位置的扩散方式没有发生变化，说明Cr 原子对C原子的扩散方式没有影响。

图6 C在α-Fe和α-Fe(Cr)中不同扩散路径的最小能量路径对比Fig.6 Comparison of minimum energy paths of different diffusion paths in α-Fe and α-Fe(Cr)

最后，研究了扩散激活能随C-Cr 距离的变化情况，建立4×4×4的α-Fe模型，计算了2种体系中C原子的扩散激活能，α-Fe(C)体系中C原子的扩散激活能为0.93 eV。

α-Fe(C)-Cr中，由图2可知C原子从Cr的第1～2，2～3，3～4，4～5，5～8，8～9 和9～11 近邻位置的扩散距离都为0.5aα-Fe，所以计算了这些近邻位置之间C原子的扩散激活能，计算结果如图7所示。由图7可见：随着距离增加，扩散激活能逐渐变大，然后逐渐趋于稳定。通过计算得到，C原子从1～2近邻位置的扩散激活能为0.88 eV，从9～11近邻位置的扩散激活能为0.92 eV。C原子离Cr原子越远，体系的能量越低，这表明当Cr 原子和C 原子离得越远，结构越稳定。

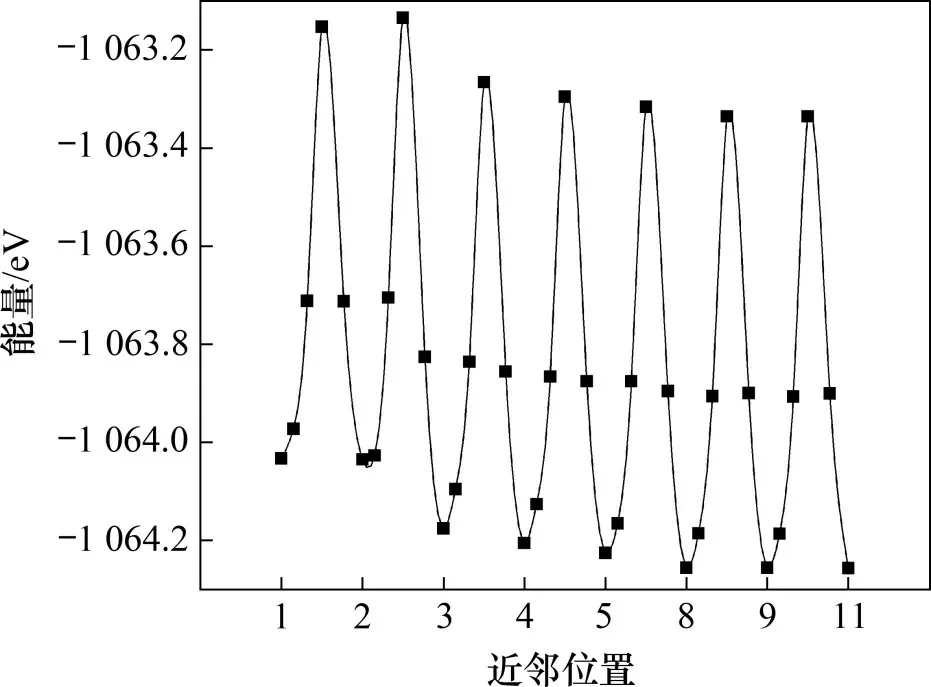
图7 α-Fe中Cr原子周围不同近邻位置间C原子的扩散激活能变化Fig.7 Variation of diffusion activation energy of C atom around Cr atom in α-Fe

3 结论

1)C 原子在α-Fe 内占据八面体位置，Cr 原子在α-Fe中随机替代Fe原子，Cr原子加入α-Fe(C)中后与Fe 原子和C 原子形成了离子键，有较好键合作用，增强了晶胞稳定性，其中Fe和Cr的成键占主要作用。

2)Cr 原子和C 原子在α-Fe 中相互排斥，随着距离增加其相互作用能越来越弱，体系能量越低，结构越稳定，在距离超过约1.75aα-Fe时，相互作用能趋于0。

3)Cr 原子加入α-Fe(C)后，当C 原子朝着远离Cr 原子的方向扩散时，Cr 原子与C 原子之间的相互作用降低了其扩散激活能，且随着C-Cr 间距离增加，扩散激活能逐渐趋于α-Fe(C)体系中C 原子的扩散激活能。