聚焦问题解决过程 指向数学能力发展

曹冠军

【摘   要】聚焦问题解决过程，引导学生采用“四自评价”的学习方式，明白所要解决的问题，找到解决问题的策略，反思解决问题的结果，总结解决问题的经验，提高学生发现和提出问题、分析和解决问题的能力，让学生真正成为学习的主人，学会学习。

【关键词】问题解决;四自评价;能力发展

在数学教学中教师要引导学生学会自问，学会自我评价，组织学生经历自理、自探、自省、自悟的“四自评价”学习过程，逐渐提升学生的数学素养。

一、“理”题意

能否正确理解题意是问题解决的关键，教师应引导学生自问：我知道了什么？通过自我评价学会简化、提炼题目信息，对关键信息展开联想，实现信息的延伸。

（一）我会简化

【案例1】分段收费

某市出租车计费方法如下：3km以内10元;超过3km的部分，1km1.5元（不足1km的按1km计算）。妈妈打出租车行驶的里程是8km，需要付多少钱？

层次一：我会用列表法和图示法简化题目信息（如图1）。

层次二：基价费+超量计价费=总金额，分段收费和“部分+部分=总数”的结构相似（如图2）。

层次三：生活中的电费、水费、停车费也会用到这样的数学結构。

学生用直观的数学语言来理解和表述题意，还原知识的本意，概括出数学知识的结构，实现实际问题与数学问题模型的转化。

（二）我能联想

【案例2】圆柱与圆锥的练习

一个圆柱的体积和底面积分别于一个圆锥的体积和底面积相等，圆柱的高是9cm，圆锥的高是（    ）。

层次一：等底等高的圆柱和圆锥体积比是3∶1，圆锥的底面积不变，体积要扩大3倍，只能高扩大3倍（如图3）。

层次二：我能用列表法（如图4）解题，圆柱和圆锥的体积和底面积都相等，所以我用等号把它们连接起来，假设圆柱的底面积是1cm2，通过它们的关系可以求出其他未知的量。

通过梳理，将文字转化成图形和表格等形式，学生就能很快厘清图形间的数量关系，很好地将关注点由“如何通过计算去求得未知数”转向“相关信息之间的关系分析”。这样通过信息间的联想，培养学生计算前“想图形”的意识，发展空间观念。

二、“探”策略

学生理解题意后，教师应引导学生自问：我会怎么解答？通过自我评价把题目中的关系用线段图等可视化工具表征出来，把内隐的关系外显化，厘清数量关系。

（一）我会用图示表征

【案例3】小数加减法

有一筐苹果，连筐重76千克，卖出一半后，连筐重38.8千克，原来苹果和筐各重多少千克？

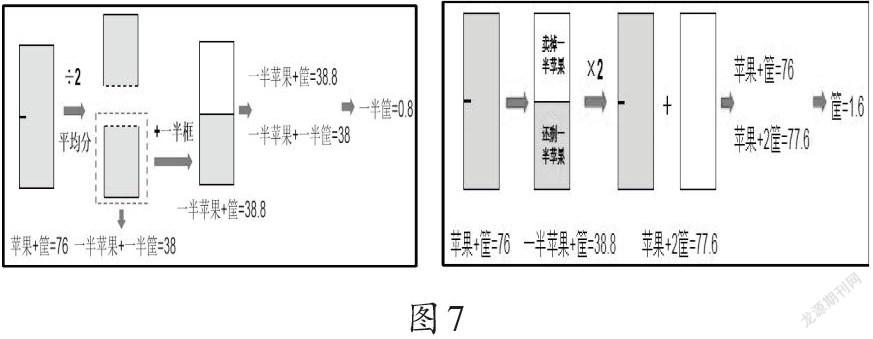
层次一：我知道76÷2表示什么。把一筐苹果“劈”成两半，76÷2表示半筐苹果和半个筐的重量之和（如图5）。

层次二：我会用图示表征找到其中的数量关系（如图6），我发现卖出的苹果是原来苹果的一半，剩下的苹果也是原来的一半，卖出的苹果的数量等于剩下的苹果的数量。

层次三：我能借助图式的有序变化发现新的数量关系，比较两个数量关系，通过相互抵消求出另一个量（如图7）。

层次四：我会创编题目（如图8），倒出前后的质量差就是倒出的几份，可以求出倒出的一份是多少。

学生通过自探，分析产生错误的原因，强化对单位“1”的理解。借助直观图式，厘清数量关系，从具体形象思维慢慢向抽象逻辑思维发展。

（二）我能多元表征

【案例4】分数乘法的意义

3/4×1/3表示什么意思？

各层次表述如表1所示。

矩形图、线段图是常见的数量关系多元化的表征方法，教师需要引导学生围绕相关概念的本质，对不同的表征进行合理、科学的分类和归纳，实现深度学习。

三、省“结果”

学生解决问题后，教师应引导学生自问：我解答得正确吗？通过自我评价不断强化学生自我检验和反思的能力，从而积累大量的学习经验，逐渐形成严谨的学习态度。

（一）我会一题多解

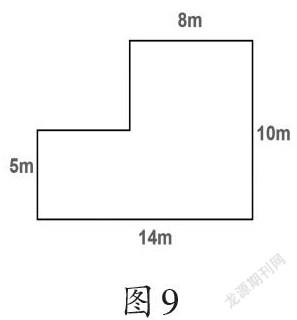
【案例5】组合图形的面积

老师计划在客厅（如图9）铺地板。请帮老师计算需要多少平方米的地板。

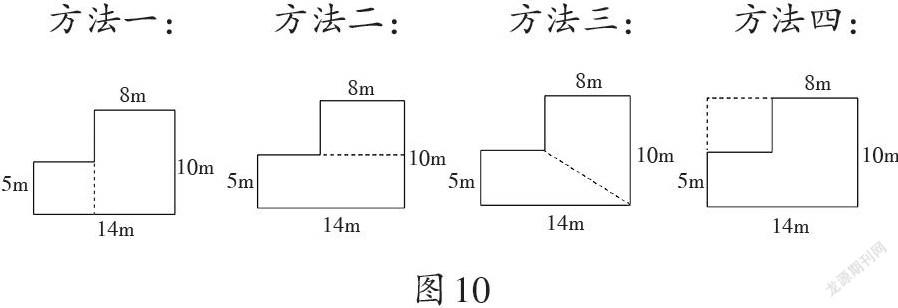
层次一：我知道求组合图形面积的一般方法——割和补。我能找到转化后图形的条件，并利用面积公式求出其面积（如图10）。

层次二：我还能利用倍积变形方法来求组合图形的面积（如图11）。

层次三：我能利用分割后两个图形的宽相等，把两个图形转化成一个大长方形（如图12）。

学生通过自省，不仅能够检验答案的合理性，也可以发现解题策略的多样性。学生不仅掌握了求组合图形面积一般的方法，还想到了倍积变形，充分利用条件，进行转化。最后完成对思路的整合：不规则图形转化为规则图形。

（二）我能解释答案

【案例6】用字母表示数

三个连续的自然数，最小的是N，最大的是（    ），这三个数的和是（    ），它们的平均数是（    ）。

第三个填空学生利用平均数=总数÷个数，列出了算式（3N+3）÷3，教师引导学生自问：还能继续化简（3N+3）÷3吗？

层次一：我能够利用图示法，移多补少，求平均数（如图13）。

层次二：我把3N和3看作两部分：字母和数字，结合图式，先把3N平均分成3份是N，再把3平均分成3份是1（如图14）。

层次三：结合图式，3N+3相当于3个N+1，相当于利用乘法分配律提取公因数3（如图15）。

学生能够借助求平均数最原始的方法——移多补少，直观形象地展示出结果，借助图示表征，把抽象的数学知识、运算定律和直观的图形结合起来，实现多角度分析数学知识，从不同层次进行数学理解，验证结果的合理性。

四、“悟”思想

学生解决问题后，教师应引导学生自问：我解决了什么问题？帮助学生认识到知识背后的数学实质，感悟知识所蕴含的数学思想和方法，让知识变薄，让思维变厚。

（一）我会举三反一

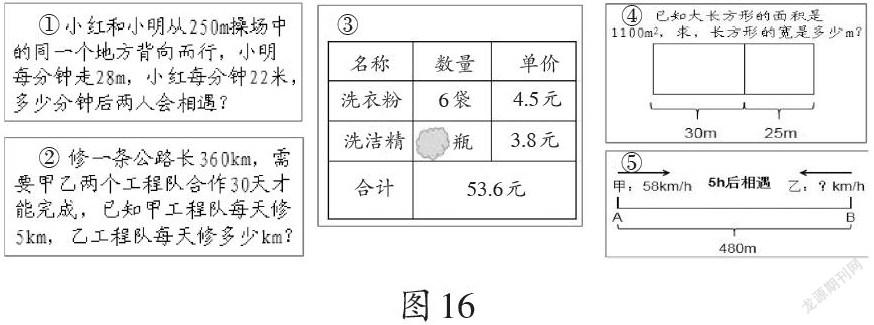
【案例7】列方程解决问题（如图16）

层次一：我可以将①②题转化成类似④⑤题中的矩形图和线段图来进行表征。

层次二：我把①②④⑤归为一类，可以用ax+bx=c的模型表示，x表示a和b两者之间相同的量。

层次三：我认为它们的数量关系都是“部分+部分=總量”，可以用ax+by=c的模型表示，只是有些x和y相等，有些x和y不相等。

学生通过自悟，加强知识和方法间的联系，将知识和方法进行分类，实现知识和方法整体性的建构，完成了从特殊到一般模型ax+by=c的归一，很好地揭示了知识的本质，有效地锻炼了学生整体把握知识和方法的能力。

（二）我能举一反三

【案例8】组合

甲、乙、丙、丁四人进行乒乓球比赛，每两人之间只比一场，一共要进行多少场比赛？

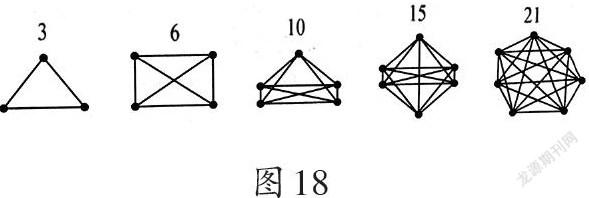
层次一：我能用连线、枚举、搭配等方法（如图17）计算出3+2+1=6（场），发现总场次数等于每人比的场次数依次连加（如表2）。

层次二：如果有32人进行比赛，计算过于麻烦。用表格法记录比赛场次（如表3），我发现其中有一半是重复的，所以4×3÷2=6（场），我可以归纳出简洁的方法：总场次=人数×场次÷2（如表4），4个量中只要知道其中1个量就能推导出其他3个量。

层次三：这个规律与打电话问题、握手问题以及“图形与几何”中有几个顶点可以连几条线的现象是一样的（如图18）。

层次四：数线段、数角、等差数列等问题也可以用这种方法解决（如图19）。

链接1：数线段问题  链接2：排列问题  链接3：等差数列

借助“同构关系”的算式，让隐性的计算方法显性化。借助直观的列表法，通过观察、分析，归纳出简洁的方法：总场次=人数×场次÷2，并发现4个量之间的关系，深化对规律的理解。激活链接，体会知识方法、策略中的不变，实现旧认知到新认知的自然贯通，帮助学生及时总结学习经验。

总之，在问题解决的过程中，教师要培养学生自主学习的能力，引导学生学会自问，学会自我评价自己的思维过程和结果，及时地进行反思和总结，不断地提高数学素养。学生学会自问、学会自我评价是一个循序渐进的过程，只要教师在教学中足够重视，并不断地总结经验，完善策略，学生自主学习的能力一定会得到长足的发展。

（浙江省杭州市萧山区临江新城实验小学   311200）