手动驾驶-CACC自动驾驶车辆混合交通流建模与仿真
侯培国,曹 军
(燕山大学 电气工程学院, 河北 秦皇岛 066004)
传统交通系统中,由于手动驾驶者对周围交通状况与前车运动状态的反应判断能力的限制、个人驾驶方式、心理差异性等,是导致交通流不稳定、出现时走时停现象、引发交通拥堵与安全等问题的重要原因.协同自适应巡航控制(Cooperative Adaptive Cruise Control,CACC)技术使用车联网技术获取周围车辆的运动状态,通过车头间距误差以及速度差来控制自身速度,可以在微观车辆层次改进交通流特性,从而减少交通堵塞与安全等问题.目前,国内外学者们已经在该领域做了很多研究.加州大学伯克利分校PATH实验室[1]提出CACC自动驾驶车辆跟驰模型,并进行小规模真车实验.Yu等[2-3]使用跟驰模型模拟ACC/CACC车辆运行情况.Van等[4]进行的小规模的ACC/CACC真车实验让ACC/CACC车辆在行车舒适度、通行效率、油耗以及温室和污染气体排放量等方面的改善得到验证.秦严严等[5]提出以速度为变量的非线性函数车头间距CACC自动驾驶车辆跟驰模型,数值模拟分析不同混合比例下CACC自动驾驶车辆混合交通流的通行效率、碰撞安全、油耗、气体排放问题.王祺等[6]在ACC/CACC模型上构建根据安全距离的自动驾驶模型,得到不同混合比例的混合交通流基本图,结论显示自动驾驶交通容量增大、交通流的动态特性提升.覃频频等[7]基于CACC模型结合Mathlab与CarSim软件搭建车辆-环境仿真平台,在平台上进行红灯状态、隧道和匝道通行环境的仿真实验,证明车队可以顺利通过三种场景.邱小平等[8]在经典的NaSch模型中采用Gipps车辆安全距离,建立了手动-自动驾驶车辆混合交通流元胞自动机模型,采用数值模拟研究了自动驾驶车辆参与的交通流的特性.陈时东等[9]提出了一个由两种车身长度不同的自动驾驶并具有定速巡航行驶的车辆组成的混合交通流模型,根据模型仿真结果得出不同混合比例的混合交通流基本图,分析了不同参数下混合交通流的特性.陆丽丽等[10]基于元胞自动机和交通流理论,构建CACC交通流模型,研究CACC车辆通讯概率、占比率、DSRC有效距离等参数之间的联系.
元胞自动机[11]特点为时空、状态离散化、相互作用的局域化和动力学演化同步性等,能够研究由大量个体互相作用而形成的复杂现象,而交通流的复杂性和离散性与元胞自动机的特性相匹配,适合仿真宏观交通流特性已得到国内外学者的认可.目前自动驾驶车辆交通流研究主要采用Gipps模型、Arnab Bose自动驾驶模型、博弈模型以及各类改进的传统跟驰模型等与元胞自动机理论、元胞传输模型、各类交通仿真软件仿真结合的方式.本文作者采用经过小规模真车实验的PATH实验室CACC车辆跟驰模型与元胞自动机理论结合,建立基于安全车间距的CACC自动驾驶与传统手动驾驶车辆混合交通元胞自动机模型.研究不同比例的CACC自动驾驶车辆混合交通流的特性;同时考虑混合交通流中手动驾驶车辆前车为CACC车辆时,对混合交通流特性的影响.
1 单车道混合模型的建立
1.1 建立模型的基本假设
研究涉及的CACC自动驾驶是基于运用车联网技术获取到周围车的行驶状态,由其控制系统控制实现的全自动驾驶.在混合交通场景中,CACC自动驾驶车辆可以通过明显的颜色、外观特征或者标识被手动驾驶员所识别.根据信息效用WUNDT曲线,随着手动驾驶员对CACC车辆了解,恐惧和顾虑会呈曲线上升至峰值再下降,以及Howard[12]等的问卷调查表明接近一半的受访者觉得自动驾驶汽车可以和手动驾驶汽车一起行驶,但是超过三分之一的受访者认为应该使用独立车道,所以设定在手动驾驶车辆行驶过程中,当前方车辆为CACC自动驾驶车辆时,手动驾驶者有不同程度的顾忌,从而会产生增大安全间距的行为.
1.2 定义安全车距
车头时距[13](Time Headway,TH)是交通系统中前后车辆的车头行驶至同一位置时刻之差.通常数值上为前后车辆的车头间距和后车瞬时速度之比,即ht=dn(t)/vn(t).最短车头时距为前后车辆车头时距范围的最小值,即保证车辆行驶安全的最小距离.车间距如图1所示.

图1 车间距示意图
当道路上存在属性不同车辆而产生的不同最短车头间距,前车为CACC自动驾驶车辆时,人类驾驶员会因心理因素使车头间距增大,这时车头间距如图2所示.
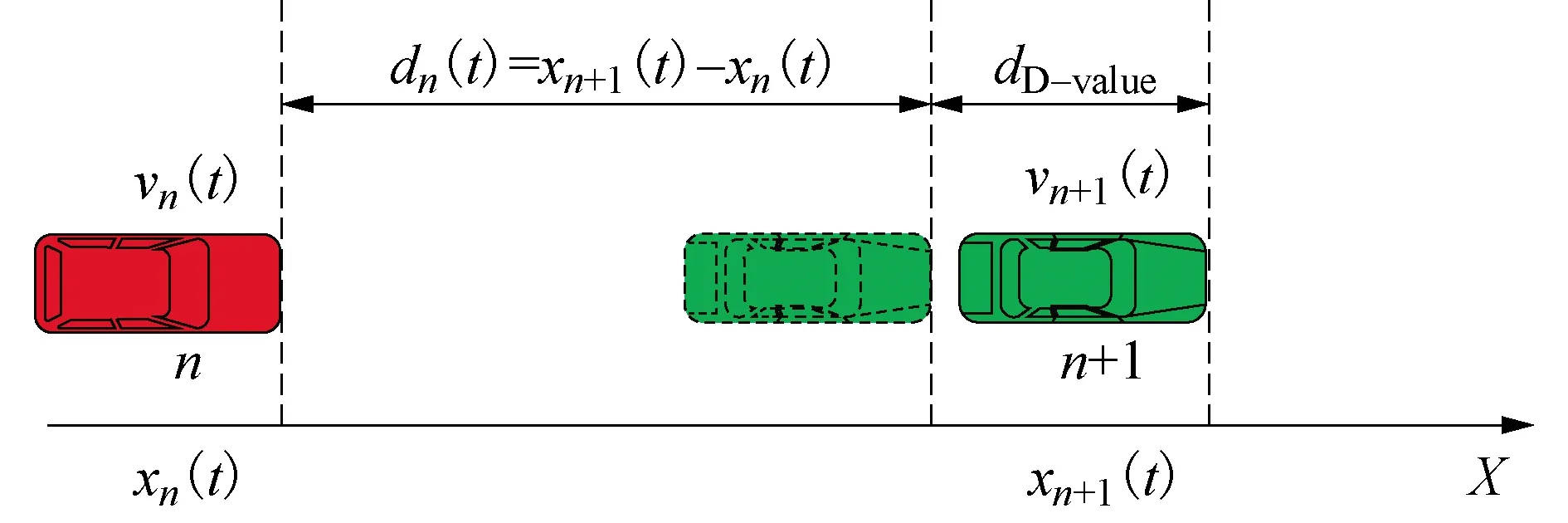
图2 混合交通流车间距示意图
由此可以得出安全车距的表达式为
Gapsafe,n(t)=vn(t)ht-ln+dD-value
(1)
式中:ht是常量,表示车头时距;xn(t)表示第n辆车在t时刻时的位置;dn(t)表示车辆n在t时刻车头与前车车头之间的距离;vn(t)表示车辆n在t时刻的速度;ln表示前车的车身长度;dD-value为前车为自动驾驶车辆,由于人类司机心理影响因素影响对原来的安全间距所增加的差值.
1.3 模型的建立
将规定长度的单车道分割为L长度的一维离散格点链,随机分布总数为N的不同比例CACC车辆与手动驾驶车辆[14-15],两种类型车辆长度均设置为一个格点长度,在任何一个时刻t,每个格点或被两种类型车辆之一占据,或者为空.所有车(n=1,2,…,N)的状态由初始位置与速度决定,其中速度vn为{0,1,2,…,vmax}范围内随机取值;dn(t)=xn+1-xn-ln表示第n辆车与第n+1辆车之间的车间距.
1.3.1 传统手动驾驶模型
根据文献[11,14]和对交通实测数据分析,确定性减速过程更有可能发生在随机减速过程之后,以及避免出现NaSch模型中只要车辆前方有空元胞,便会行驶到前车后一个元胞,手动驾驶模型在减速过程中,建立对确定性减速过程进行改进的NaSch模型,采用判断车间距与安全距离大小,确定是否进行安全性减速.手动驾驶车辆模型演化规则如下:
1)加速过程.
(2)
2)以概率P随机减速过程.
(3)
3)车辆进行确定性减速以及安全性减速,但速度不小于0.
vn(t+1)=
(4)
4)更新位置.
xn(t+1)=xn(t)+vn(t+1)
(5)
1.3.2 CACC自动驾驶模型
模拟CACC自动驾驶车辆采用基于PATH实验室跟驰模型[1]来确定加速度,根据自动驾驶特性,通过安全距离与车间距比较直接决定采用加速、匀速、减速之一行驶,避免如NaSch模型先加速再减速以及随机慢化,并在车间距较小时采用安全性减速,演化规则如下:
1)确定速度变化量.
en(t)=dn(t)-Gapsafe,n(t)
(6)
dvn(t)=k0vn+1(t)+k1en(t)+
k2(vn+1(t)-vn(t))
(7)
式中:en(t)为车间距与安全车距的差距;dvn(t)为速度变化量.
2)根据dn(t)与Gapsafe,n(t)的大小,决定车辆进行加速、匀速、减速运动.
vn(t+1)=
(8)
式中:[dvn(t)]为不小于dvn(t)的最小整数.
3)更新位置.
xn(t+1)=xn(t)+vn(t+1)
(9)
2 数值模拟与讨论
2.1 模型参数取值与仿真设置
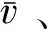
ρ=N/L
(10)
(11)
(12)
2.2 基本图分析
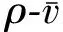

图3 不同混合比例下的基本图
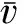

表1 不同混合比例下基本图的数据

图4 CACC车辆与SDNaSch模型基本图
2.3 时空图分析
图5为密度ρ=0.16时,不同比例的混合交通流500至1 000时间步的时空演化图,横轴代表空间,纵轴代表时间,黑点代表此格点被车辆占据,白色代表无车辆占据.灰色范围代表车辆自由通行;黑色的条纹区域代表车辆聚集到一起形成局部堵塞.
由图5(d)图可知,r=1(道路上全为自动驾驶车辆)时,其交通流特性与传统交通流不同,CACC自动驾驶车辆以相对稳定的速度行驶,又由于仿真实验采用周期性边界,在时空演化斑点图上呈现均匀周期化变化,车流处于畅通运行状态.由图5(a)~(c)可知,随着r值的增加,车流堵塞区域减少,堵塞带减小以及变窄,车间距减小,车流运行斜率减小,平均速度增加.图5(c)清楚地显示了堵塞相与运动相组成的相分离现象,此时交通流处于亚稳定状态,符合实际交通流实测.仿真结果表明:增加CACC车辆所占比例,可以有效提升交通效率,提高车流的平均速度,增加车流量,降低交通堵塞现象.

图5 不同混合比例下的时空斑点图
2.4 车头间距分析
车头间距作为微观参量,与宏观参数密度、流量、平均速度有紧密联系,车头间距会因为交通流状态的差异,而表现出不同的特征.根据人类司机心理影响因素对自动驾驶车辆安全净距增加差值dD-value的不同取值,研究混合交通流的运行状态和头间距dn(t).r=0.5,dD-value取不同数值时的时空斑点图见图6.
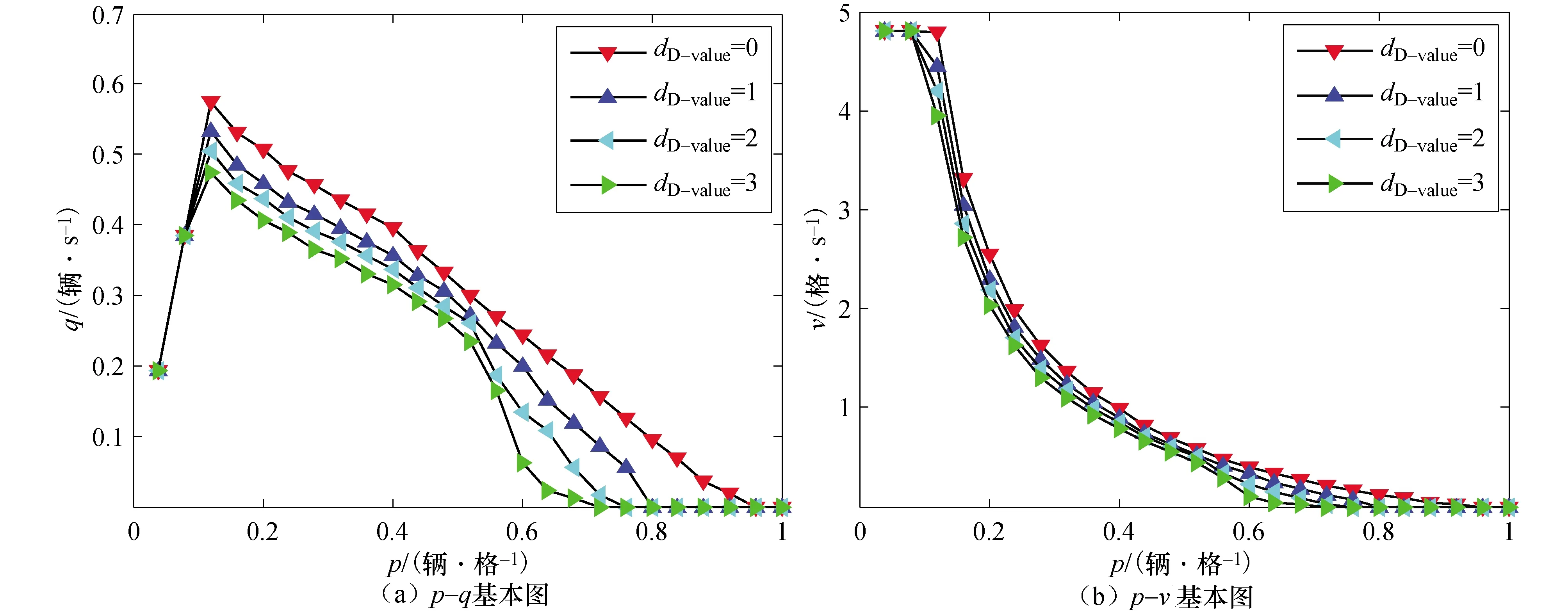
图6 r=0.5,dD-value取不同值时基本图
图7为ρ=0.16、P=0.2、r=0.5时,dD-value取不同数值的车间距三维图.结合图6和图7可知,在其他参数相同情况下dD-value值逐渐增大时,传统手动驾驶车辆的安全距离增加使车间距变大,导致混合交通流流量和平均速度降低,特别在中高密度区,下降度较明显,形成严重的交通堵塞,通行能力大幅度下降.

图7 不同dD-value值车间距三维图
为了深入研究车间距对传统手动驾驶与CACC自动驾驶混合交通流的特性影响,对相邻的两种不同属性组合的车辆进行4种情景下模拟,得出不同车型的车间距和后车速度对比如图8所示.
图8列举了一次模拟实验中(ρ=0.16、P=0.2、r=0.4)同一时刻起100个时间步,起始车距相同,图中空间单位为格,红色实线为后车与前车的车间距,黑色实线为后车的速度.图8中前车的属性不同,后车的速度变化有很大差异,如图8(a)、(b)所示,当后车为手动驾驶车辆时,由于手动驾驶车辆不能及时地根据车间距来控制速度,造成车间距过大,贴合度过低,甚至会因为前车为CACC自动驾驶车辆时,驾驶者对其顾虑,会进一步增大车间距,过大的车间距对交通流的整体平均速度影响较大,从而影响整个交通流,造成堵塞;如图8(c)、(d)所示,当后车为自动驾驶车辆时,能较好地根据车间距及时地调整车速使车间距保持在合适的区间,车间距与后车的速度二者变化紧密贴合,尤其如图8(d)所示,当前后车辆均为CACC自动驾驶车辆时,车间距与后车速度的波动幅度、频率更小从而使交通流更加稳定,且后车保持较高速度的时间步有所增加.
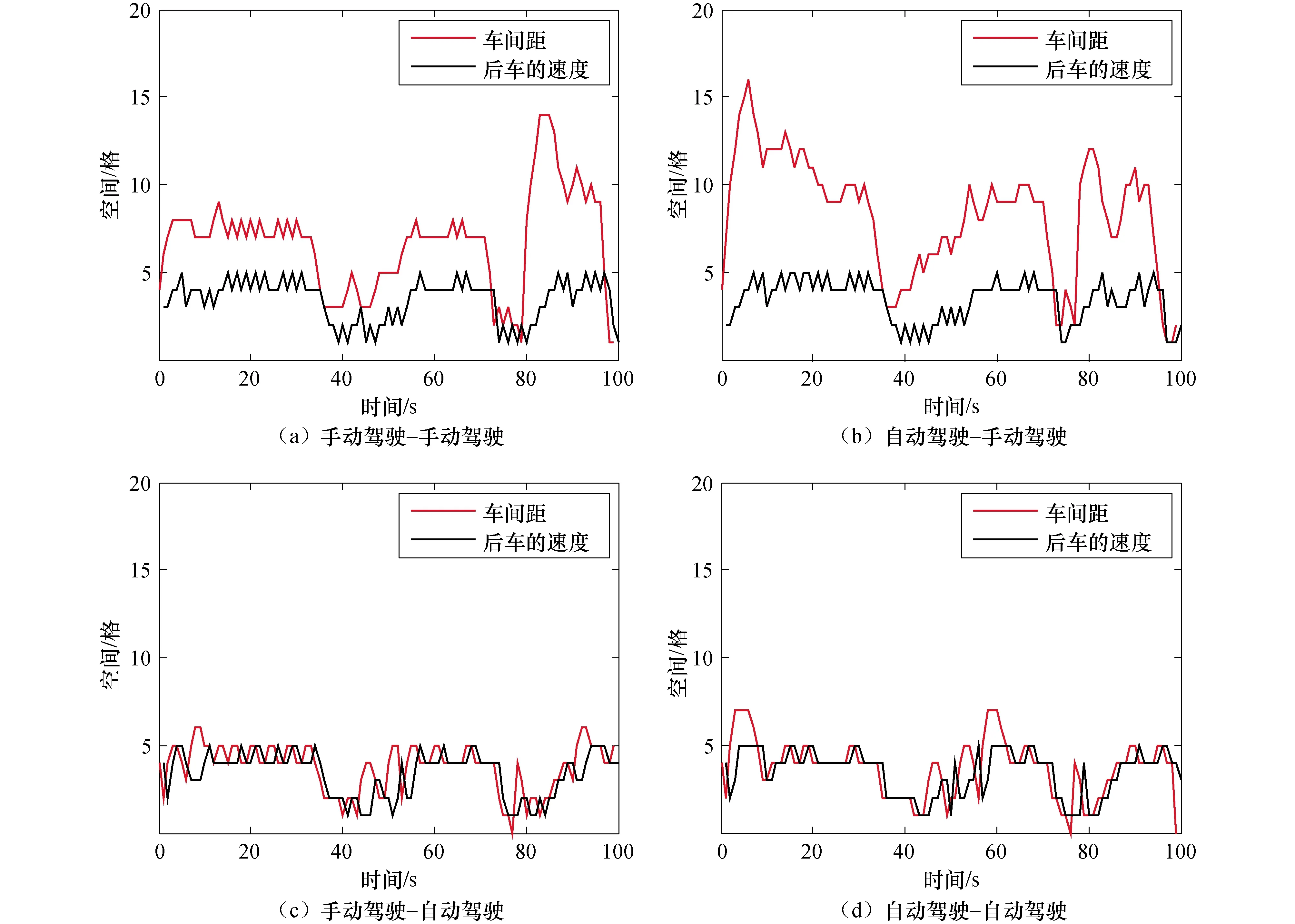
图8 四种情境下车间距和后车速度对比图
3 结论
1)以Nasch元胞自动机交通流模型为基础,考虑传统手动驾驶员的心理因素与驾驶行为差异化,建立手动驾驶-CACC自动驾驶混合交通流模型,通过数值模拟得出结果,混合交通流的流量-密度关系符合交通流特性.混合交通流中出现堵塞相与运动相组成的相分离现象,交通流处于亚稳定状态,符合实际交通流实测.

3)通过分析传统手动驾驶者心理影响因素为切点,研究手动驾驶-CACC自动驾驶车辆交互在混合交通流中产生的影响,当手动驾驶员对自动驾驶车辆的安全顾虑越大时,手动驾驶车辆安全距离越大,会导致车间距过大,前后车的速度调节同步率低,从而使交通流流量、平均速度、截止密度下降,这一现象在高密度区域尤其显著.

