城市轨道交通盾构区间纵断面线形节能优化

王仲林,杨冬营,易思蓉

(1.广州地铁设计研究有限公司, 广州 510010;2.西南交通大学 a.土木工程学院，b.高速铁路线路工程教育部重点实验室，成都 610031)

节能降耗是各类工程项目的研究难点.城市轨道交通运营中的能耗成本占总运营成本的20%以上，列车运行能耗又占总能耗的50%以上[1].城市轨道交通非明挖地下区间纵断面线形不受地形限制，设计灵活，但对列车运行能耗影响较大.我国城市轨道交通中，地下段占运营线路总长的75%以上[2]，施工措施多为盾构法，而盾构区间纵断面线形节能设计一直是线路设计的难点.当两站中心标高相差不大时，国内外学者总结出节能型纵断面线形的两项基本特征：高站位、低区间的“V”型坡利用功能转换方式实现节能，站外的第一纵坡被称为节能坡.对于列车运行最高速度为80 km/h的线路，李文波等[1-3]建议节能坡的长度为250 m，坡度取2%～2.6%间.胡晓丹等[4]则给出了不同区间长度的节能坡建议值.Kim等[5]定量分析了“V”型坡的节能效率.在“V”型坡的基础上，当区间中部形成高点时，纵断面线形又被称为“W”型坡.何麟辉等[6-8]对站间不同坡度组合进行仿真分析后发现，“W”型坡较“V”型坡更节能，并且“W”型坡更利于区间排水和泵房设计.

一般来说,符合基本特征的人工设计纵断面线形难以与列车运行状态相吻合，节能效果有限.当两站中心标高加大时，基本特征也逐渐失去适用性.针对人工设计的不足，国内学者提出了多个基于种群算法的轨道交通纵断面线形节能优化模型.白骁等[9]以牵引能耗最小为优化目标，建立城市轨道交通纵断面线形节能优化模型，并分析了单面坡、“V”型坡、“W”型坡的适用情况和优化结果.温馨等[10]则同时考虑能耗和工程费两项指标建立三种坡型的节能优化模型.陈进杰等[11]基于高速列车节能操纵优化问题的数学描述，提出工况序列表与遗传算法相结合的高速铁路纵断面线形节能优化模型.但目前的节能优化模型较难适应纵断面线形设计环境多变的情况.

针对现有研究的不足，本文作者以变坡点的里程和高程做为决策变量，将变量分配与编码过程相统一，考虑各类几何约束与设计条件约束，以列车双向运行能耗为目标函数建立纵断面线形节能优化模型，采用粒子群优化(Particle Swarm Optimization,PSO)算法进行模型求解.同时拟定多阶段的优化策略，逐步改进变坡点的数量和分布，使优化模型具有通用性.

1 优化模型

1.1 决策向量与编码

轨道交通纵断面线形上的竖曲线半径只取若干定值，为简化优化模型，可选择变坡点的里程和高程作为变量，并记纵断面线形的决策向量为[M1,E1,M2,E2,…,Mn,En]，n为变坡点数量，且同样为变量.约定每个变坡点在各自的控制矩形内变动，控制矩形由相互垂直的两条线段H1H2、V1V2确定，如图1所示.变坡点PI在线段H1H2和V1V2上的投影点分别为Ph和Pv，线段H1H2和V1V2的交点为Pj，H1H2与水平轴的夹角为αh.

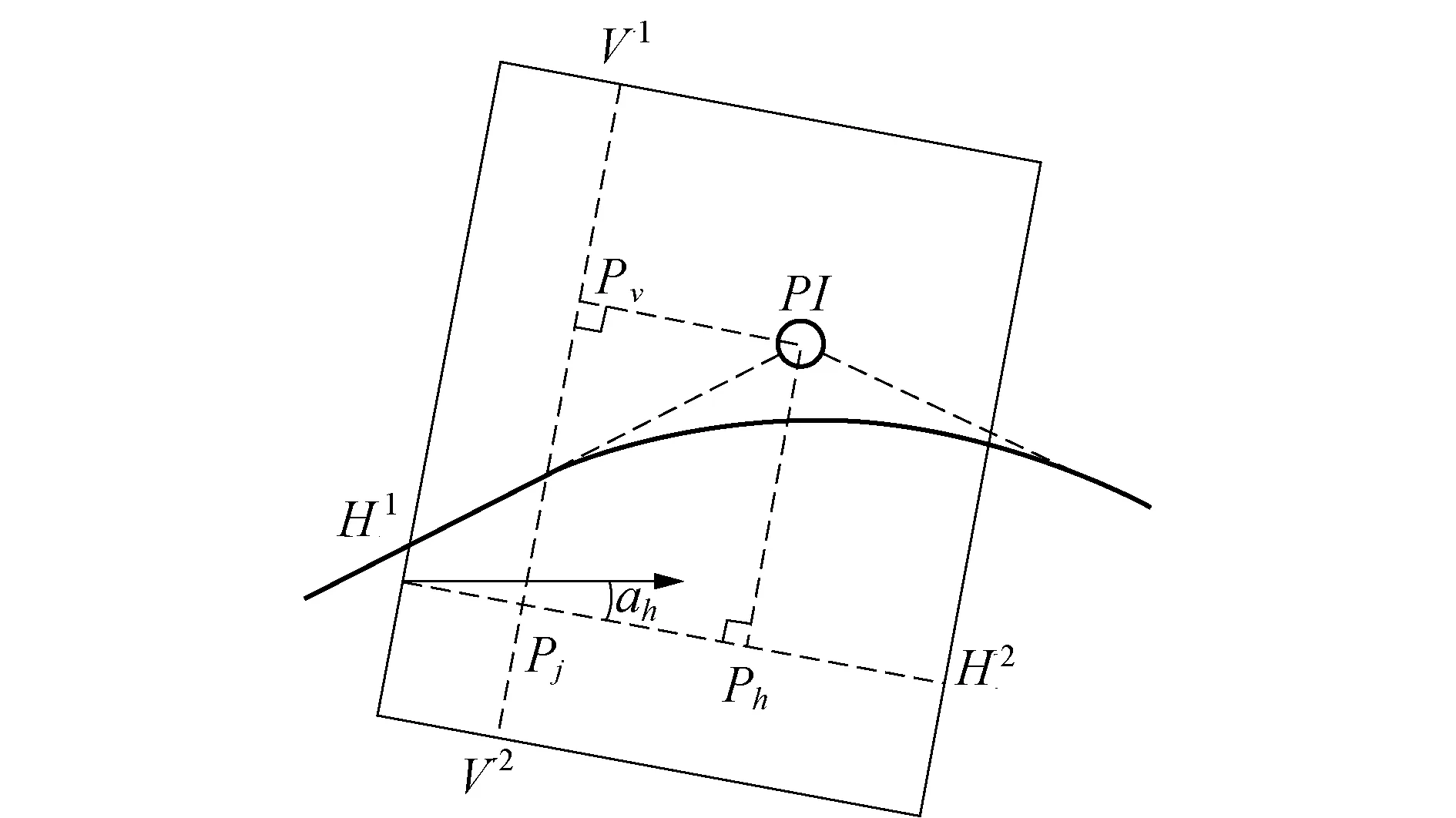
图1 变坡点取值范围与编码参数

为使变坡点坐标能在矩形范围内均匀分布，可利用线段H1H2、V1V2所确定的局部坐标系，将纵断面线形决策向量的各维编码成[0,1)间的随机数，记为[C1,C2,…,Cm]，其中0≤Ci<1,m=2n.当需要对实际纵断面线形进行牵引能耗计算时，再将编码向量解码为实际的纵断面决策向量，解码公式为

(1)

(2)

(3)

1.2 目标函数

列车运行能耗主要包括列车牵引能耗和控制系统的基本能耗，其中控制系统能耗占比较小，可予以忽略.王月明[12]给出了按电机输入功率计算列车牵引能耗的方法.由于城市轨道交通规范要求上、下行隧道间最多间隔600 m设置一处联络通道用于安全疏散，且不能设置台阶或大坡度，这使得上、下行纵断面线形应保持高度基本一致的相同坡向.因此，可假定上、下行方向纵断面线形相同，以列车双向运行的牵引能耗为优化目标函数，即

MinC=C上+C下=

(4)

式中:C上为上行方向的牵引能耗；C下为下行方向的牵引能耗；Pi为牵引工况下，列车当前速度所对应的电机输入功率,kW.图2给出了某4动2拖列车编组电机输入功率曲线图；Δti为列车运行计算时间间隔,s，若采用时间作为计算步长，Δti为定值；η为牵引逆变器电气效率.

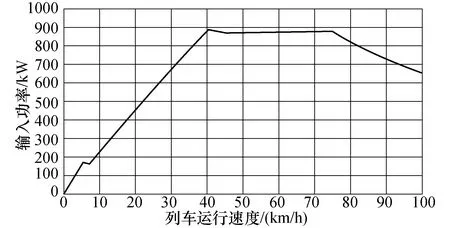
图2 牵引工况下列车输入功率曲线

依据决策向量值和选取的竖曲线半径，可计算出纵断面线形，通过列车运行计算得到对应的双向运行速度-距离曲线，再结合列车输入功率曲线，按式(4)计算出列车双向运行牵引总能耗.

1.3 约束条件

列车运行计算前，纵断面线形还应满足现行设计规范中的几何约束和工程中的设计条件约束.

1.3.1 几何约束

1)坡度约束.

区间坡度的约束表达式为

(5)

2)夹直段长度约束.

竖曲线间夹直段长度表达式为

Mi-Mi-1-(Ti+Ti-1)≥Ljmin

(6)

式中：Ti、Ti-1分别为第i、i-1个变坡点处的切线长.

3)竖曲线进站约束.

第一竖曲线和末位竖曲线不能进入车站有效站台或车站结构范围.当站端设置配线时，竖曲线还应避开道岔区域.定义L1表示第一竖曲线起点距离线路起点的最小长度要求，L2表示末位竖曲线终点距离线路终点的最小长度要求.竖曲线进站约束表达式为

(7)

式中：Ms为线路起点里程；Me为线路终点里程；T1为第一个变坡点处的切线长；Tn为第n个变坡点处的切线长.

1.3.2 设计条件约束

1)线路埋深约束.

考虑到盾构隧道施工可能引起的地面隆沉对临近地面建筑和地下构筑物的影响，以及盾构推力对地下管线的影响，盾构法施工的区间隧道覆土厚度不宜小于隧道外轮廓的直径D[13].因此，地面线以下约(2D-s)米范围是纵断面线形的禁区,s为轨面到隧道外轮廓底的距离.

2)结构物约束.

城市内地下结构物密集，盾构隧道常需下穿或上跨结构物，形成标高上的约束范围，例如：地下污水管、楼房的筏板基础、相邻线路隧道等.当平面线路与结构物交叉范围不长时，可按最不利点原则将结构物约束转化为纵断面线形必须绕避的一个或两个垂直线段.确定垂直线段范围的关键参数是施工安全净距.结构物约束的公式为

(8)

式中：h上为结构物顶标高；h下结构物底标高；a为施工安全净距(常与D相等)；E为相应里程处的线路标高.

1.4 列车操纵策略

纵断面线形的优化目标是通过坡度和坡长的调整，延长惰行时间，避免不必要的列车制动，减少有害坡段[14].因此，列车操纵策略是节能运行的关键.城市轨道交通列车采用无级调速模式时，可依据运行速度确定工况转换时机[15].本研究采用牵引-惰行-制动模式仿真列车运行，用四个工况转换速度阈值控制列车操作，如图3所示.k1与m2是惰行转其他工况的阈值，k2是牵引终止阈值，m1是制动终止阈值.

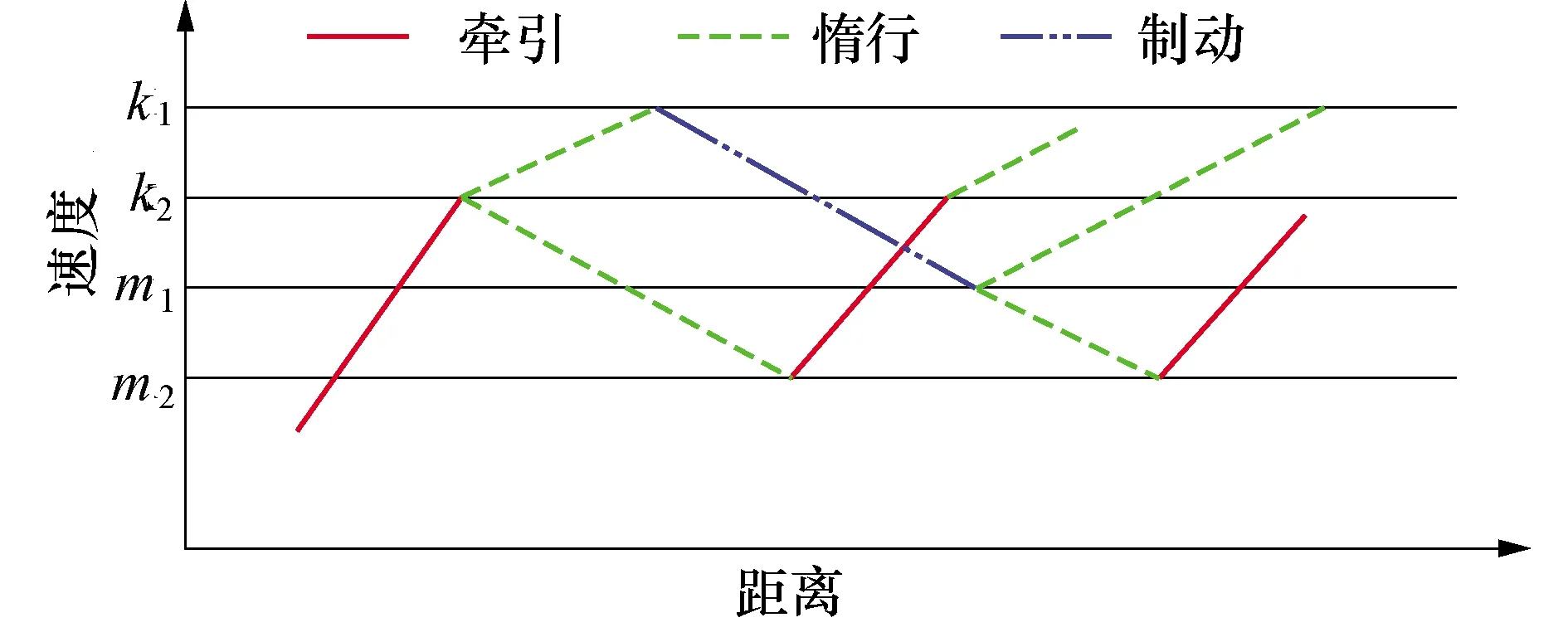
图3 工况转换模式

综上所述，城市轨道交通盾构区间纵断面线形节能优化模型可表述为

MinC=C上+C下

s.t.g(M,E)≤0

(9)

2 模型求解

2.1 标准PSO算法

由Kennedy 提出的标准PSO算法是一种依靠群体智能的优化算法.该算法通过模拟鸟群和鱼群活动，利用种群内的合作与竞争，实现个体位置和种群最优位置的提升[16].

标准PSO算法的数学描述为：对于一个d维空间优化问题，第i个粒子的位置和速度可分别表达为Xi=[xi,1,xi,2,…,xi,d]T和Vi=[vi,1,vi,2,…,vi,d]T，每个粒子在自身轨迹上的最好位置为Pi=[pi,1,pi,2,…,pi,d]T，至第g次迭代前种群的最好位置为Pgbest，则第g+1代粒子的飞行速度被更新为

vi,g(g+1)=w×vi,j(g)+c1×r1×

(pi,j-xi,j(g))+c2×r2×(pgbest-xi,j(g))

(10)

式中：w是惯性权重；c1和c2为学习因子；r1和r2为服从均匀分布U(0,1)的随机数；i=1,2,…,n为粒子规模.当w取0.729 8，学习因子c1和c2取1.496 18时，算法具有较好的收敛性[17].依据新的速度值，每个粒子的位置被更新为

xi,j(g+1)=xi,j(g)+vi,j(g+1)

j=1,2,…,d

(11)

当种群最优位置不变，或达到最大迭代次数时，优化过程终止.标准PSO算法还需设置粒子的最大速度区间[-Vmax,Vmax]，Vmax取0.3Xmax.粒子飞行速度越界时置0.标准PSO算法只针对无约束优化，应用于约束优化时应增加边界和约束处理.

2.2 边界处理

工程优化中，变量都有各自的取值范围.Venter通过改变粒子飞行速度来进行边界处理[18]，即当决策向量中的某个分量越界时速度分量的计算公式为

vi,j(g+1)=c1×r1×(pi,j-xi,j(g))+

c2×r2×(pg,j-xi,j(g))

(12)

新的速度会使粒子位置分量向种群最优位置和自身轨迹最优位置移动，从而指向变量的可行区域.

2.3 约束处理

1)几何约束处理.

当纵断面线形不满足几何约束条件时，可能无法形成合理的空间线形，或受列车牵引性能限制，无法进行正常的列车运行计算.借鉴差分进化算法中的直接比较法来处理几何约束，可避免不必要的列车运行计算[19].其处理原则包括：当原最优粒子和新的粒子存在约束冲突时，约束冲突数量少者更优，若约束冲突数相等，则保留原最优粒子；当原最优粒子和新的粒子均不存在约束冲突,则运行能耗低者更优.

2)设计条件约束处理.

在目标函数中引入惩罚因子，可处理设计条件约束.设置惩罚因子参数时，考虑逐步引导粒子向非约束区域过渡.包含惩罚因子的目标函数为

(13)

式中：o1为线形与禁区的交叉次数;ua为禁区约束惩罚单价;li为第i次交叉长度;o2为线形与结构物约束线段的相交次数;ub为结构物标高约束惩罚单价;lj为交点至约束垂直线段某端点的距离;Lj为结构物约束线段的总长.

2.4 多阶段优化策略

1)初始方案搜索.

当仅明确两站坡度和中心标高时，应通过假设变坡点的分布来进行初始纵断面线形的搜索.初始方案搜索阶段变坡点控制矩形的布置如图4所示.矩形位置由步长S、矩形宽度W，以及纵断面最大坡度G三个参数确定，其中S≥W.首末位控制矩形上的线段V1V2长度为0，以保持车站坡度不变.其余控制矩形上，H1H2为水平线段，V1V2为垂直线段，且两线段的交点在区间线路起终点间的连线上.

图4 初始方案搜索中变坡点控制矩形分布

考虑到坡段长度不宜小于列车长度，步长和矩形宽度可取列车长度.由于此步变坡点数量较多，为避免几何约束阻碍最优线形的搜索进度，竖曲线半径可取为0.优化结果为拆线式的初始纵断面线形.

2)深度优化.

深度优化前，应删除既有方案上坡段长度或坡度代数差较小的变坡点.优化中，竖曲线半径应取设计值，每个变坡点控制矩形上，线段H1H2可适当加长，V1V2则应适当减小.图5给出了深度优化阶段变坡点控制矩形的布置方法.若此步优化结果上仍然存在坡段长度小或坡度代数差小的变坡点，可删除后进行下一轮深度优化，直到优化结果满意为止.

图5 深度优化阶段变坡点控制矩形分布

基于上述优化模型及其求解方法，开发了相应的“城市轨道交通盾构区间纵断面线形节能优化系统”，优化流程框架如图6所示.

图6 纵断面线形节能优化框架

3 算例研究

以成都地铁7号线火车北站至驷马桥站盾构区间为案例进行优化分析.区间设计速度80 km/h，两站中心标高差6.96 m，均为0.2%的下坡，车站中心间距2 018.53 m，有效站台长140 m.纵断面线形下穿北新高架桥桩基形成结构物约束，下穿沙河形成线路埋深约束的主要控制点.

3.1 参数配置

基本参数取值如表1所示.当站端竖曲线半径为3 000 m时，首末位变坡点距离区间线路起终点的距离一般不超过50 m，因此在两变坡点的控制矩形上，H1H2=50 m，V1V2=0，并在各优化阶段保持不变.中间变坡点控制矩形分布需兼顾坡段长度不宜小于列车长度的规范要求[19]，依据不同优化阶段进行分配.各优化阶段种群中的粒子数均为100.

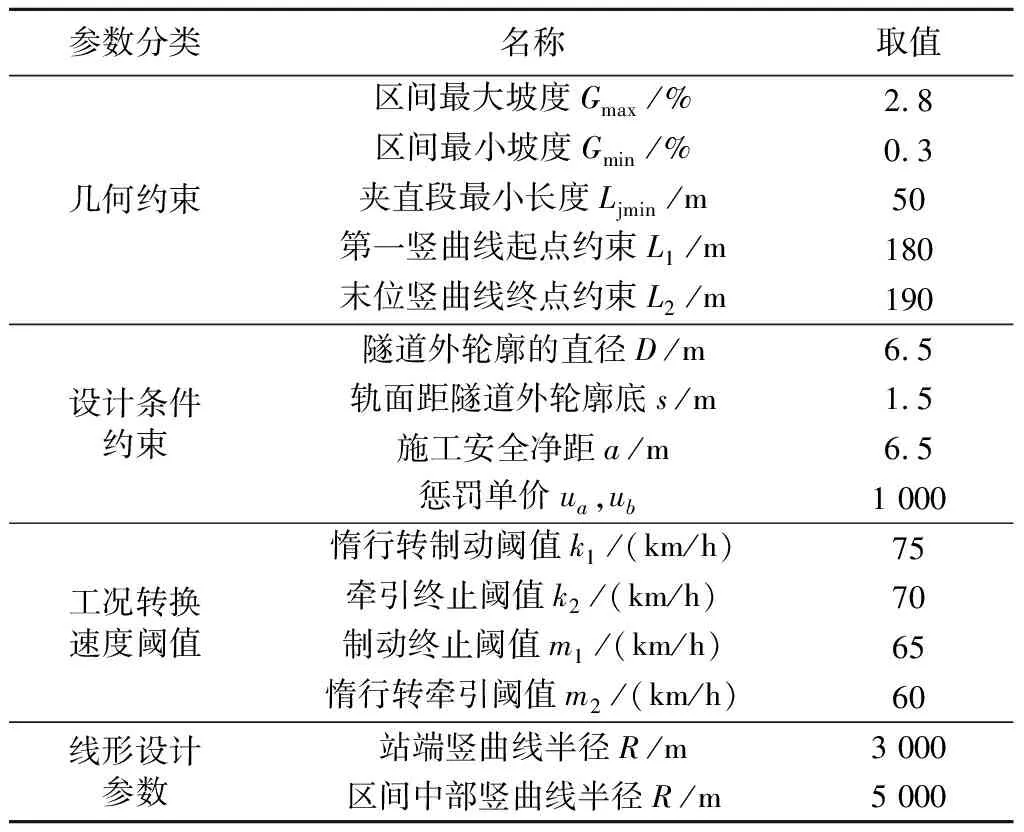
表1 基本参数取值

3.2 优化过程

在初始方案搜索阶段，按步长S=140 m，宽度W=140 m分配中部变坡点控制矩形.图7给出了初始方案搜索阶段种群最优方案的能耗变化线，计算用时169.1 s，循环1 300代.在第67代之前，最优方案未完成几何约束处理，能耗值无穷大.在第67代至831代，最优方案未完成设计条件约束处理，能耗值极大但不断递减.第831代后，最优方案完成约束处理并在1 300代稳定在43.178 3 kW·h.

图7 初始方案搜索阶段最优值变化线

优化方案及VS曲线如图8所示,在初始方案基础上，逐步删除虚线处的变坡点进行三次深度优化.深度优化过程中，中间变坡点控制矩形的中心与各既有变坡点重合，并使H1H2=140 m，V1V2=10 m.

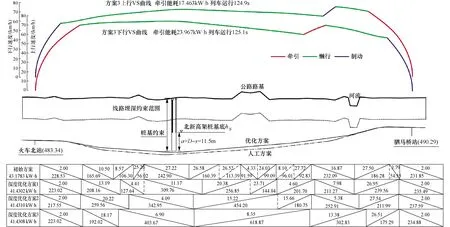
图8 优化方案及VS曲线

另外，既有线形方案被编码为种群中的一员，以便在深度优化中加快约束处理，提升收敛速度.3次深度优化平均计算用时218.7 s，能耗均略大于41.430 kW·h.

3.3 优化结果分析

人工方案及VS曲线如图9所示.对比图8、图9可知，优化方案与人工方案一样，均避开了北新高架桩基约束范围，但优化方案线路整体埋深稍浅.两侧节能坡对比，优化方案较人工方案长度短，坡度缓，中间坡段对比，两者相近.

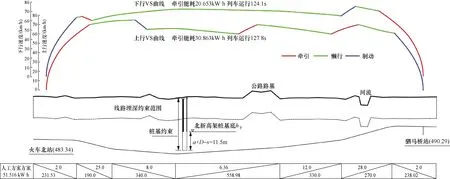
图9 人工方案及VS曲线

由于两站高差较大，桩基约束又压低了区间中部标高，优化方案和人工方案均无法避免区间中部的牵引和制动.但在上行方向上，人工方案的出站节能坡度大、坡段长，在达到最低点前，惰行速度增加快，触发了区间制动.过最低点后，面临大坡度，人工方案又触发了两次区间牵引.优化方案没有区间制动，仅在进站前需要一次区间牵引；在下行方向上，人工方案出站后加速快，较优化方案制动早，且制动距离稍长.在进站前人工方案坡度较大，惰行减速快，触发了一次区间牵引，而优化方案没有区间牵引.

人工方案双向运行总时间为251.9 s，总能耗为51.516 kW·h，而优化方案双向运行总时间为250.0 s，总能耗仅为41.431 kW·h.优化方案较人工方案节能19.6%，且列车运行时间稍短.

4 结论

1)构建了以节约双向牵引能耗为目标的城市轨道交通盾构区间纵断面线形节能优化模型，改进PSO算法，并基于多阶段优化策略，实现了变坡点分布未知和已知情况下的纵断面线形优化.

2)通过边界和约束处理上的改进，PSO算法在工程优化中具有较快的收敛速度.

3)变坡点的数量和取值范围是影响纵断面线形节能效果的重要因素，分阶段的优化策略可逐步确定合理的交点分布，提升了优化模型的通用性.

4)工况转换模式显著影响节能优化结果.应根据不同的区间长度、限速范围、车站高差等拟定不同的工况转换模式来引导纵断面线形优化进程.

5)本文仅以固定的速度阈值来控制列车的工况转换，没有考虑列车运行控制上的节能.在节能控制策略下，优化方案的上行方向和人工方案的下行方向，进站前的牵引运行可转变为惰行.如何将纵断面线形的优化与节能控制策略的优化相结合是下一步的研究重点.