ISOP-DAB变换器动态特性及回流功率混合优化控制技术

农仁飚，杨晓峰，周兵凯，李继成

(1.北京交通大学 电气工程学院，北京 100044；2.新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司)，北京 100192)

随着新能源发电装置、储能设备及以电动汽车为代表的新型不确定性电能负荷的接入，传统电网在接纳大规模分布式能源方面的不足日益凸显[1].而以电力电子能量路由器(Electrical Energy Router, EER)为代表的柔性接入方式是解决该问题的有效手段，并逐渐发展成为电力能源互联网的核心基础设备[2-3].其中，双有源桥(Dual Active Bridge，DAB)变换器因具备功率双向传输、电气隔离、易于实现软开关等诸多优点，并能通过串并联组合实现模块化方案，近年来被广泛应用于新能源发电、电动汽车及储能等能源变换系统[4-6].此外，输入串联输出并联双有源桥(Input Series Output Parallel Dual Active Bridge，ISOP-DAB)变换器将多个DAB变换器通过模块化组合，可有效降低电气应力同时增强冗余运行能力[7]，已发展成为EER的直流级变换拓扑之一[8].

ISOP-DAB变换器可有效提升变换器电压等级，但也保留了DAB的基本特性.单移相(Single Phase Shift，SPS)控制[9]通过调节原副边交流方波电压之间的移相角，控制功率传输的大小和方向.但当输入输出电压与高频变压器变比不匹配时，系统回流功率增加，软开关范围减小[10].扩展移相(Extended Phase Shift，EPS)控制在原边或副边的H桥内引入一个内移相角，增加了控制自由度[11].在此基础上，文献[12]基于动态小信号模型，提出可有效减少变换器回流功率和电流应力的控制策略，但仅分析了输入电压与输出电压变比相匹配的情况.此外，双重移相(Dual Phase Shift，DPS)[13]、三重移相(Triple Phase Shift，TPS)[14]等优化控制被相继提出，在增加控制自由度的同时也增加了变换器工作模态，使得组合系统数学模型更加复杂[15].上述方案虽然在一定程度上实现了DAB变换器回流功率优化，但在模块化组合下系统回流功率优化仍需进一步探索.

实现ISOP-DAB变换器输入电压均衡以及输出电压稳定，提升系统动态特性是控制目标之一.如果系统各模块电路参数一致，采用共同占空比控制即可实现直流电容电压稳定[16].然而，由于实际电路参数差异将导致模块间功率传输不平衡[17].文献[18]提出一种双环控制，在共同输出电压闭环控制的基础上，增加输入均压闭环以校正各模块功率实现平衡，但未进一步优化系统动态响应.文献[19]提出三环控制策略，即在双环控制策略的基础上增加了电流内环，提高了系统动态响应，但是对通信要求高，可靠性低.为了提高变换器的动态响应，诸如模型预测控制(Model Predictive Control，MPC)等非线性控制理论也被应用于直流变换器[20]领域.文献[21]对直流降压变换器中采用状态空间平均法建模，实现了双环模型预测控制，但仅对单个变换器下应用效果进行分析.文献[22]利用模型预测控制解决了多变换器并联时传输功率不均衡的问题，同时提高了变换器在电压跳变或负载突变的响应速度，但没有进一步分析输入串联情况下的电压均衡问题.

因此，本文作者在ISOP-DAB变换器状态空间平均化方程基础上，分析EPS控制下的回流功率和电流应力；同时以优化ISOP-DAB变换器的动态特性和回流功率为目标，提出一种基于EPS控制的输入电容电压均衡和输出电压稳定的模型预测及梯度下降算法(Model Predictive Control and Gradient Descent Algorithm，MPC-GDA)，进而实现了系统的混合优化控制.最后通过仿真对比验证了所提控制策略的有效性.

1 基于扩展移相的ISOP-DAB变换器

1.1 ISOP-DAB变换器

ISOP-DAB变换器拓扑如图1所示.Us与iinp分别为电源电压和电流.第i个DAB变换器的原边全桥H1i输出电压和副边全桥H2i输入电压为Uabi(i=1,2,…,m)和Ucdi；Uout为输出电压.iLi和iouti分别为第i个DAB变换器的电感电流和负载电流；原边侧输入电流和副边侧输出电流为iLpi和iLsi；icini和icouti分别为第i个DAB变换器的输入和输出电容电流；S1-S8为DAB变换器开关管.

由图1得ISOP-DAB变换器原边侧电路方程为

图1 ISOP-DAB变换器

(1)

ISOP-DAB变换器副边侧电路方程为

(2)

式中：rs为电源侧等效内阻；Li为高频隔离变压器Ti的等效漏感；Cini和Couti为第i个DAB变换器的输入和输出电容；RL为负载；m为DAB变换器单元的数量；变压器变比为n.

1.2 扩展移相控制状态空间平均化方程

为得到变换器数学模型，以第i个DAB变换器为例进行分析，其在EPS控制下的工作波形如图2所示.其中，Ths为半开关周期，UL为电感电压，Pt(EPS)为传输功率.D1i定义为开关管S1(S2)和S4(S3)之间的内移相比，0≤D1i≤1；D2i为H1i和H2i之间的外移相比，0≤D2i≤1且0≤D1i+D2i≤1.由此可知在EPS控制中，不仅包含原副边全桥之间的外移相比D2i，同时在H1i中还引入了内移相比D1i，进而使H1i输出电压Uabi波形为三电平波；通过调整内移比D1i可减小DAB变换器的整体回流功率并增大功率传输范围.为简化分析，令ki为电压转换比，表示为ki=Ucini/(nUout).

由图2知，当DAB变换器进入稳定运行状态之后，其电感电流正负对称，t0-t8为一个周期内电感电流斜率变化时间点.其中t0、t1和t3时刻的电感电流为

图2 EPS控制工作波形图

(3)

式中：fs为开关频率.

进一步可得EPS控制下的传输功率Pti(EPS)为

(4)

其相应的输出电压状态空间平均化方程为

Ucini-iouti

(5)

同理，EPS控制下的输入侧支撑电容电压的状态空间平均化方程为

(6)

1.3 回流功率与电流应力对比分析

由EPS工作模态分析可知，第i个DAB变换器单元在EPS控制下的回流功率Pbfi(EPS)为

Pbfi(EPS)=

(7)

选取EPS控制下传输功率参考值为PNi，电流应力参考值为INi，满足

(8)

同理可得SPS控制下的回流功率Pbfi(SPS)和传输功率Pti(SPS)表达式分别为

(9)

式中：Di为SPS下的移相比.

将式(7)～式(9)标幺化得

(10)

由此可得Di、D1i和D2i之间的关系为

4Di(1-Di)=

4D2i(1-D2i)+2D1i(1-D1i-2D2i)

(11)

SPS控制下的移相比Di可由EPS控制下的内移相比D1i和外移相比D2i表示为

(12)

根据式(10)～式(12)分析，相同传输功率且电压转换比为ki=3时，标幺化回流功率Mbfi随着D1i和D2i在SPS与EPS控制下的三维曲线如图3所示.在SPS控制下，回流功率随着D2i变大而增大.在相同传输功率的情况下采用EPS控制时，系统回流功率显著降低.因此，相对SPS控制，EPS对回流功率有较好的抑制效果.

图3 回流功率Mbfi随着移相比D1i和D2i变化的三维曲线

同时，在不同的电压转换比ki下，SPS和EPS控制下所对应的回流功率曲线如图4所示，其中case1为D1i=0.2,D2i=0.3；case2为D1i=0.5,D2i=0.3.

图4中SPS和EPS控制下系统回流功率Mbfi均会随着ki的增加而逐渐增大.但是在相同的电压转换比ki下，EPS控制对应变化曲线均在SPS控制下方，即采用EPS控制时系统的回流功率较小.此外，当ki过大时，回流功率的急剧增加，不利于系统的稳定运行，因此设计ISOP-DAB变换器电路参数时，应尽量避免出现在较大的电压转换比ki下运行.

图4 回流功率Mbfi随着电压转换比ki的变化曲线

EPS控制下的电流应力iLimax(EPS)表达式为

[ki(1-D1i)+(2D1i+2D2i-1)]

(13)

SPS控制下的电流应力iLimax(SPS)数学表达式

(14)

根据式(8)、(13)和(14)可得SPS和EPS控制下的标幺化电流应力Ai(SPS)和Ai(EPS)表达式分别为

(15)

相同传输功率且电压转换比为ki=3时，电流应力Ai随着D1i和D2i在SPS与EPS控制下的三维曲线见图5.当采用SPS控制时，电流应力随着D2i增大而增加；采用EPS控制时，电流应力整体变化幅度更小，其电流应力曲面位于SPS控制的下方.此外，在功率传输相等工况下，采用EPS控制系统电流应力较小，因此，采用EPS控制对电流应力也有较好的改善优化效果.

图5 电流应力Ai随移相比D1i和D2i变化的三维曲线

在不同的电压转换比ki下，SPS和EPS控制下的电流应力曲线如图6所示，其中case1为D1i=0.3，D2i=0.05;case2为D1i=0.5，D2i=0.15.

由图6可知，电流应力Ai随着ki的增加而逐渐增大.相同电压转换比ki时，EPS控制下的电流应力小于SPS控制.此外，当电压转换比ki过大时，电流应力将会急剧增大，不利于系统的稳定运行.

图6 电流应力Ai随着电压转换比ki的变化曲线

2 基于EPS的模型预测控制技术

2.1 输入电容均压模型预测控制技术

EPS控制下的输入电容电压微分方程反映输入电容电压的变化趋势.因此采用前向欧拉法对其进行离散化处理可得到

[Ucini(tq+1)-Ucini(tq)]fs

(16)

将式(5)和(16)联立可得到EPS控制下的输入电容电压的预测控制方程为

Ucini(tq+1)=

(17)

其中，输入电压等效分量ρcini为

ρcini=

(18)

式中：Uout(tq)和Ucini(tq)为tq时刻的输出电压和输入电容电压采样值；Ucini(tq+1)为tq+1时刻输入电容电压预测值.

由式(17)可建立第i个DAB变换器输入电容电压的价值函数Jcini(q)为

Jcini(q)=[Uavg-Ucini(tq+1)]2

(19)

其中，Uavg为输入电容电压平均值，即

(20)

结合式(17)～式(20)，并对输入电容电压进行标幺化处理，得EPS下预测控制电容电压均衡优化外移相比D2cini为

(21)

其中

(22)

式中：Ucinpui(tq)为第i个DAB变换器输入电容电压标幺值，Ucinpui(tq)=Ucini(tq)/Uavg.

根据式(21)标幺化输入电容电压Ucinpui(tq)与预测优化电压均衡外移相比D2cini之间的关系曲线如图7所示.其中电路参数为Ucini=350 V，给定内移相比D1i=0.15，其余电路参数如表1所示.当输入电容电压与给定电压偏差较大时,系统将以最大优化能力降低(D2cini=0.5)或提升(D2cini=0)输入电容电压，从而使得输入电容电压快速调节至给定值.当输入电容电压在给定值附近时，其能够进行平滑的调节，使之快速跟踪参考值.

表1 ISOP-DAB变换器仿真参数

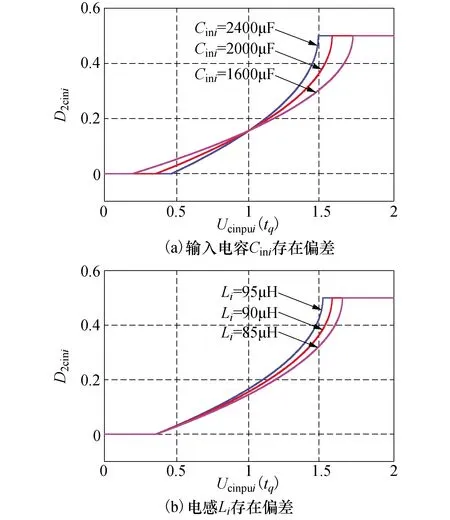
图7 D2cini与Ucinpui(tq)关系曲线

根据图7，当输入电容Cini和电感Li的测量参数值存在误差时，D2cini将会偏离真实值，导致输入电容电压存在控制偏差.此外，在实际电路运行中，由于开通关断延迟、开关管压降、变换器死区时间以及采样传输延迟等因素的影响,使得式(21)中的预测优化外移相比D2cini与实际真实值之间存在偏差，从而引起控制系统误差.为消除上述控制偏差，采用输入电容电压均衡自适应误差校正控制算法，具体校正控制方案如图8所示.

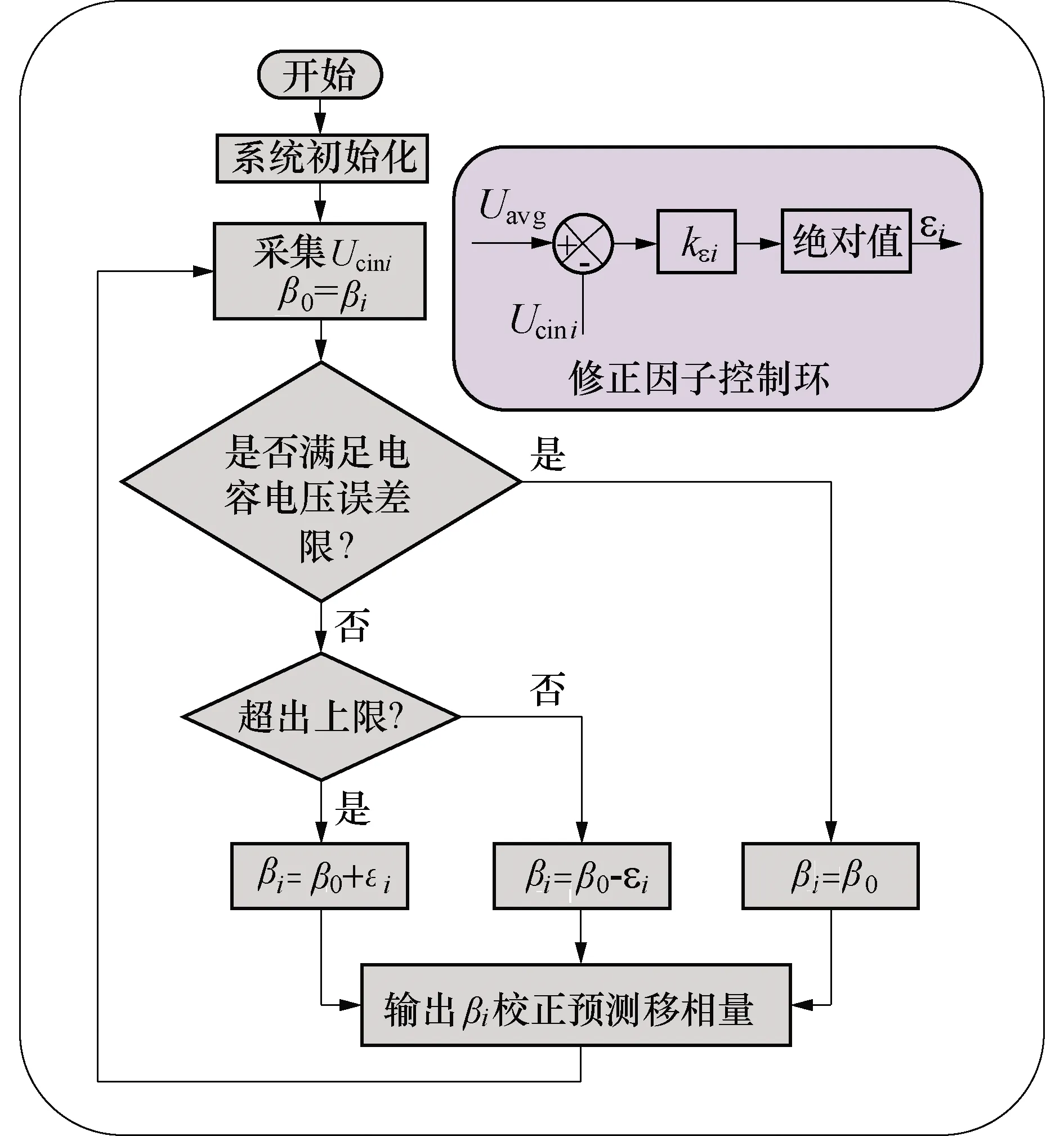
图8 电容电压均衡自适应误差校正算法流程图

其中，Uerror为输入电容电压允许误差范围，bi为预测移相校正系数，其初始化值为b0.ei为通过修正因子控制环所得到的校正系数修正因子，kei为修正因子调节系数.由此实现对电容电压均衡预测移相比D2cini的动态修正.Ucini上、下限分别为

(23)

最终得EPS控制下加入自适应误差校正系数bi的输入电容电压均衡模型预测优化外移相比D2cinfinali为

D2cinfinali=βiD2cini

(24)

2.2 输出电压模型预测控制技术

输出电容电压的微分方程可预测输出电压的变化趋势，采用前向欧拉法对输出电压微分方程进行离散化处理，可得

[Uout(tq+1)-Uout(tq)]fs

(25)

根据式(5)和式(16)可同样求得输出电压模型预测控制方程为

(26)

其中，输出电压等效分量routi为

ρouti=

(27)

式中：iouti(tq)为tq时刻输出电流采样值，Uout(tq+1)为tq+1时刻的输出电压预测值.

根据式(25)和式(26)，选取输出电压价值函数Jout(q)

J(q)=[Uoref-Uout(tq+1)]2

(28)

为匹配输出电压模型预测控制器的输入与输出，同时增强系统的稳定性与抗干扰能力，对输出电压进行标幺化处理得到优化移相比D2outi表达式为

(29)

其中，

(30)

式中：Uspu(tq)为EPS控制下系统的标幺化输出电压，Uspu(tq)=Uout(tq)/Uoref.

由式(29)得到标幺化输出电压Uspu(tq)与优化移相比D2outi之间的关系曲线如图9所示.当检测到输出电压与给定参考电压值偏差较大时，系统将以最大优化调节能力提升(D2outi=0.5)或降低(D2outi=0)输出电压，使得输出电压快速恢复至参考电压值.当输出电压接近参考值时，可平滑调节输出电压以快速跟踪输出电压参考值.

图9 D2outi与Uspu(tq)关系曲线

此外，由于实际电路中的开关管压降、电路参数测量误差以及器件内部寄生参数的影响，使得预测控制优化移相比D2outi存在偏差，进而会影响控制系统的精确性.为消除实际电路中输出电压的控制偏差，引入误差校正因子bouti对偏差进行补偿，误差校正因子控制如图10所示.其中，Kpi和Kii分别为PI控制器的比例和积分系数，Kvri为虚拟导纳前馈控制调节系数.可知，输出电压模型预测校正控制算法主要由输出电压闭环和虚拟导纳前馈控制组成.

图10 输出电压模型预测误差校正系数控制框图

最终得到加入误差校正系数bouti之后的预测优化外移相比D2outfinali为

D2outfinali=βoutiD2outfinali

(31)

则可得采用EPS控制的第i个DAB变换器的回流功率Mbfni(EPS)为

Mbfni(EPS)=

(32)

3 基于GDA的回流功率优化技术

梯度下降算法是神经网络模型训练最常用算法，也可用于求解强化学习优化问题，通过逼近所建立控制对象数学模型的极值，求得最优解[23].通过在模型预测控制基础上引入梯度下降算法，进一步实现对复杂模型的优化求解，得出预测控制量.因此，本文基于梯度下降算法对EPS控制下ISOP-DAB变换器回流功率进行优化，进而减小系统回流功率.

定义EPS控制下回流功率的梯度表达式为

(33)

式中：∇Mbfni(EPS)(D1i)为回流功率梯度.

为实现EPS控制下ISOP-DAB变换器回流功率优化，构造回流功率基本优化迭代方程为

D1i=D1i(initial)-ηi·∇Mbfni(EPS)(D1i)

(34)

式中：ηi为学习率；D1i(initial)为内移相比初始值；D1i为根据式(34)迭代更新后内移相比.

由式(34)可知，学习率ηi是优化迭代过程的主导因子，当ηi过小时，将导致系统迭代次数增加，降低收敛速度；当ηi过大时，虽然系统的迭代次数有所减少，但可能会导致系统不稳定.因此为减小求解系统回流功率优化时陷入局部最优的风险，在原有迭代方程的基础上加入冲量，形成冲量梯度下降回流功率优化算法.则原有的梯度下降方程式(34)更新为

δi=γi·δi-ηi·∇Mbfni(EPS)(D1i)

(35)

式中：δi为加入冲量优化之后的等效梯度步进数值；γi为冲量比例系数.由此得到加入冲量之后的内移相比D1i的迭代公式为

D1i=D1i(initial)+δi

(36)

由式(35)、式(36)知，D1i更新时不仅考虑了当前梯度值，而且加入了冲量γi·δi.相比原有梯度下降算法，当梯度与冲量方向一致时，冲量将会增加，可以加速系统的求解；反之当冲量减小时，将会降低系统的超调与振荡.

将梯度下降回流功率优化算法与输出电压稳定和输入电容电压均衡模型预测控制算法结合，得到基于EPS的模型预测控制与梯度下降算法回流功率混合优化整体控制如图11所示.

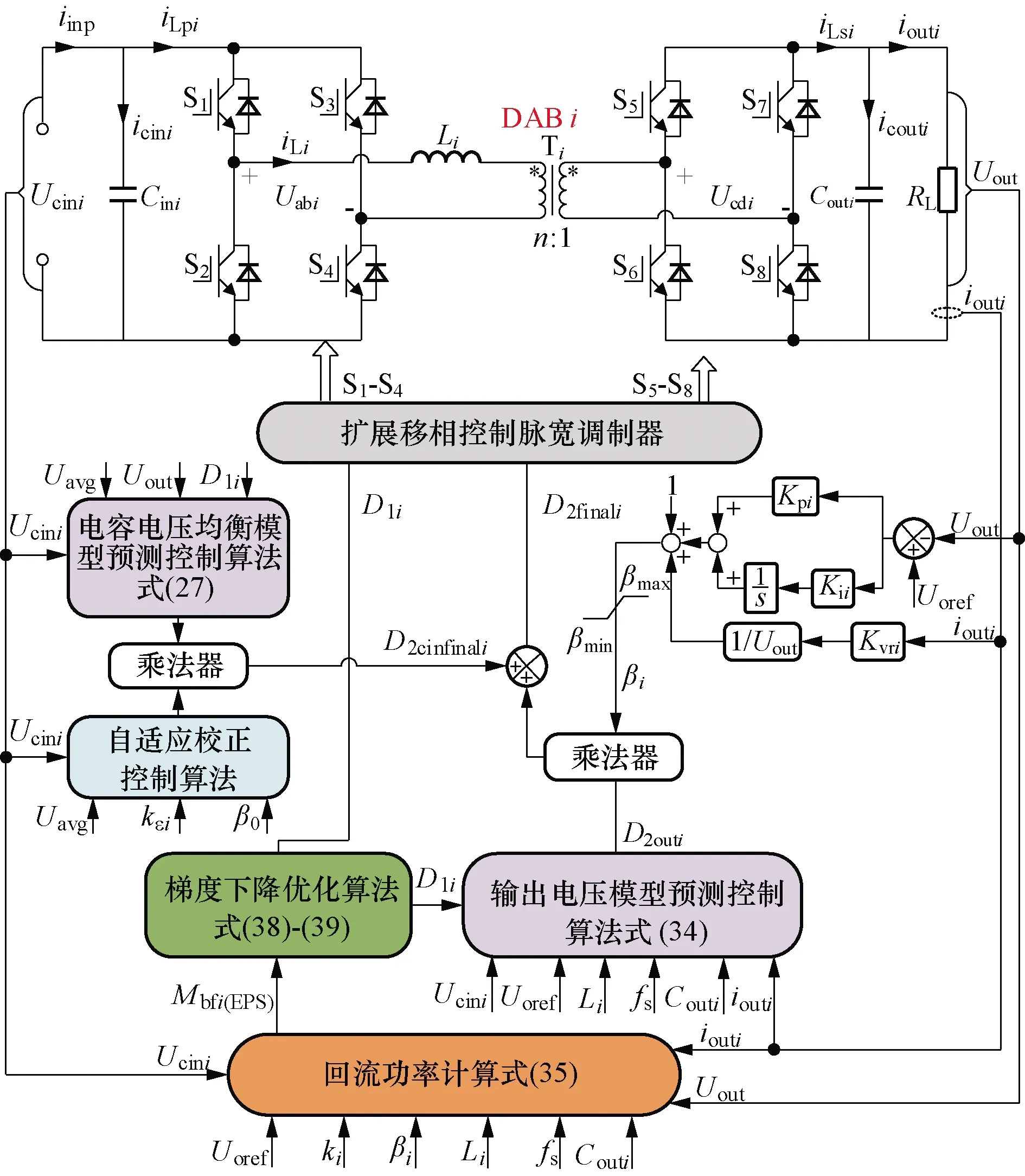
图11 基于MPC-GDA的ISOP-DAB变换器控制框图

4 仿真分析

为验证MPC-GDA理论分析准确性和优化控制策略的有效性，在Matlab/Simulink搭建基于MPC-GDA优化控制的ISOP-DAB变换器仿真模型.此外，将MPC-GDA控制同传统的SPS控制进行了对比分析，具体的仿真电路参数见表1.

4.1 动态性能验证

仿真工况1的输出电压Uout=700 V，1.6 s时刻负载由12 kW突增至13.6 kW，ISOP-DAB变换器的仿真波形见图12和图13.采用SPS控制时，ISOP-DAB变换器输出电压稳定和输入电容电压均衡控制相对应的调节时间分别为50 ms和46 ms，而当采用MPC-GDA控制时，相应调节时间仅为8 ms和27 ms，分别降低了84.0%和41.3%.此外，跟SPS控制相比，MPC-GDA控制的系统输出电压跌落由6.5 V降为1.2 V，减小了81.5%.由此可知，MPC-GDA控制与传统SPS控制具有更好的动态调节性能.

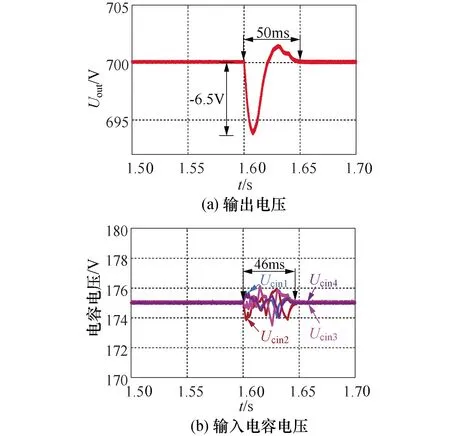
图12 负载变化时，SPS控制下的仿真结果

图13 负载变化时，MPC-GDA控制下的仿真结果

仿真运行工况2为输出电压Uout=700 V，并且ISOP-DAB变换器运行负载功率为12 kW.在1.6 s时，将输入电压突降5%.采用传统SPS与MPC-GDA控制所对应的具体仿真波形对比分别如图14和图15所示.由图14和图15可知，当输入电压发生变化时，在传统SPS控制下，ISOP-DAB变换器输出电压稳定和输入电容电压均衡控制的调节时间分别为39 ms和41 ms，而当采用MPC-GDA控制时，相应调节时间仅为8 ms和0 ms，分别对应减小了约79.5%和100%.此外，跟SPS控制相比，MPC-GDA控制的系统输出电压跌落由2.3 V降为0.6 V，降低了73.9%.可见，MPC-GDA控制具有更优的动态特性和抗干扰能力.

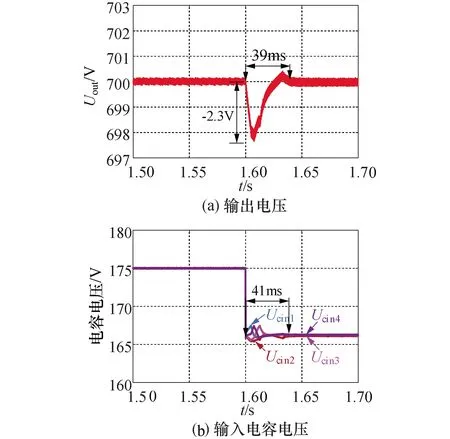
图14 输入电压变化时，SPS控制下的仿真结果

图15 输入电压变化时，MPC-GDA控制下的仿真结果

4.2 回流功率优化

当ISOP-DAB变换器的负载功率变化时，系统回流功率仿真波形如图16所示.与传统SPS控制相比，MPC-GDA控制下的ISOP-DAB变换器回流功率明显降低，几乎被完全优化至0附近；同时当负载功率发生变化时，MPC-GDA控制回流功率优化控制算法能够及时地进行优化调节，使ISOP-DAB变换器回流功率较为快速地优化在0左右，由此验证了回流功率优化算法的可行性及有效性.

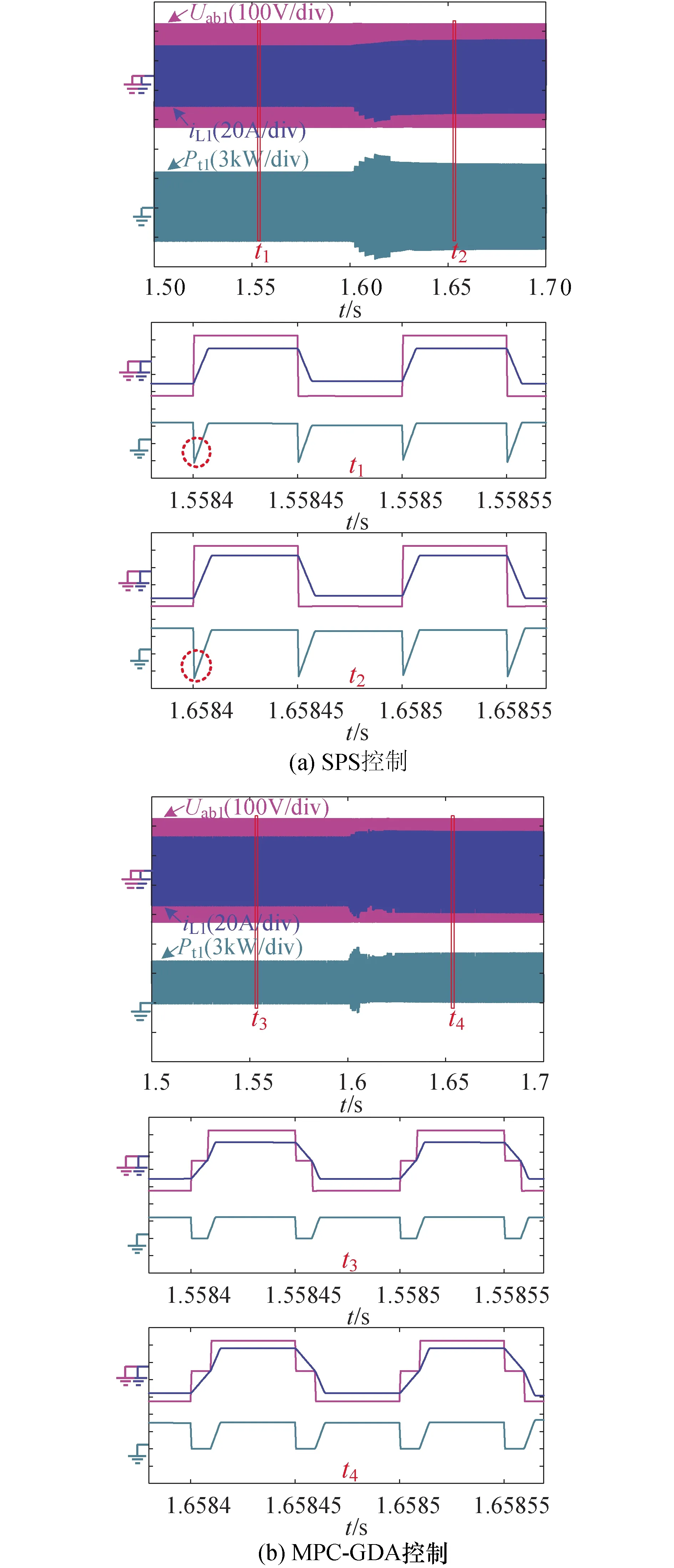
图16 负载变化时SPS和MPC-GDA控制方式下回流功率的仿真结果

同样，当ISOP-DAB变换器的输入电压变化时，回流功率仿真波形如图17所示.

图17 输入电压变化时SPS和MPC-GDA控制方式下回流功率的仿真结果

与传统SPS控制相比，MPC-GDA控制下的回流功率降低为0附近，此外，当系统的输入电压发生变化时，MPC-GDA控制亦能将ISOP-DAB变换器的回流功率快速降低到0左右.由此验证了回流功率优化算法的可行性以及良好的鲁棒性和抗干扰能力.

5 结论

通过对EPS控制下ISOP-DAB变换器回流功率和电流应力数学模型模型的推导和分析，同时考虑ISOP-DAB变换器动态性能的优化，提出了一种基于EPS的输入电容电压均衡和输出电压稳定的模型预测控制与梯度下降回流功率优化算法(MPC-GDA)的混合优化控制策略，并与传统单移相(SPS)控制进行对比，理论分析和仿真结果表明：

1)混合优化控制策略增加了ISOP-DAB变换器的控制自由度和灵活性.

2)在输入电压及负载功率突变时，混合优化控制策略有助于提高ISOP-DAB变换器的动态响应速度和抗干扰能力.

3)混合优化控制策略能显著改善ISOP-DAB变换器的回流功率.