考虑最优消纳区间的区域能源聚合商博弈策略

郑云飞，熊志，王博，潘兴亚，潘笑

（1. 国网湖北省电力有限公司经济技术研究院，湖北省武汉市 430077；2. 国网湖北省电力有限公司，湖北省武汉市 430077；3. 武汉大学电气与自动化学院，湖北省武汉市 430072）

0 引言

在世界能源短缺、环境污染严重的背景下，以风光为代表的新能源成为能源开发的主流趋势[1]。为了促进新能源的快速发展，国家不断地推动电力市场体制改革，区域能源聚合商（District Energy Aggregator，DEA）作为新型主体参与电力市场以及电网的运行和调度，将成为推动智能电网建设的重要环节。为了避免以风光为代表的新能源的大量浪费现象，研究考虑新能源消纳的区域能源聚合商博弈策略具有重要的意义。

文献[2]依据主从博弈模型考虑了新能源消纳对电力市场运行的影响，结果显示博弈参与者的利益均能得到明显提升，并且风光等新能源的弃电率也得到降低；文献[3]考虑了电力市场的运行特点及新能源消纳的要求，提出了可以促进新能源消纳的综合能源系统日前市场出清模型；文献[4]通过引入涉及多能源供应网络的主从博弈模型，分析多市场主体参与新能源消纳的互动行为；文献[5]提出了一种计及电能质量的电力市场多主体博弈模型，有效地促使售电方与大用户在双边合同市场与集中交易市场的有效平衡。以上文献都采用了建立博弈模型的形式来尽可能地追求电力市场背景下新能源消纳水平的提升，但未曾考虑新能源发电低抗扰与随机性所带来的高额消纳成本[6]。

2019年5月，为建立促进新能源消纳的长效机制，国家能源局发布了《关于建立健全可再生能源电力消纳保障机制的通知》[7]，通知明确了各地区新能源的消纳权重。据此已有部分学者[8-9]提出，通过在实际运行过程中适当弃风弃光来提高新能源的消纳能力，保证在完成新能源消纳任务的同时提高系统运行的安全性与经济性。

为此本文提出“最优消纳区间”的概念，并将其引入到电力市场的DEA博弈模型中，建立考虑各DEA底层能源调度优化及新能源最优消纳区间的主从博弈模型，并讨论主从博弈模型给电力市场所带来的效益提升问题。

1 考虑最优消纳区间的DEA博弈框架

1.1 最优消纳区间的概念

大规模地利用新能源替代传统能源可以有效地改善环境污染等问题，但是为了实现新能源的全消纳或较高比例消纳，系统往往需要付出额外的成本[10]。在我国向“清洁低碳、安全高效”的能源体系转型过程中，对地区电网及新能源发电水平进行分析，确定满足我国可再生能源发展目标的最优消纳区间，从而进一步实现以最小的全社会成本实现最大化清洁能源消费占比[11]。本文综合考虑当新能源消纳水平提升时产生的消纳成本及电网侧的电源扩容成本，对消纳水平的经济性进行分析，可以发现地区电网存在最优的新能源消纳水平。相应的，新能源消纳水平指标的经济性分析如图1所示。

从图1可以发现，B点对应的消纳水平 λB对应着最低的系统总成本，可以理解为最优消纳水平。消纳水平较低时，全社会购电成本因电源侧新能源建设运行成本过高而增加；消纳水平较高时，全社会增量购电成本因系统侧网架结构优化以及调峰的消纳成本过高而增加。同时可以发现B点附近的系统总成本变化很小，为了提升调度策略的灵活性，本文提出的最优消纳区间为[λA,λC]，基于最优消纳区间的要求，通过惩罚函数对主从博弈模型中的博弈主体目标函数进行修改，最终得到基于“最优消纳区间”的最优调度结果。

1.2 DEA的博弈框架

DEA是一个集合多种形式电能的生产、调度和销售为一体的综合服务商。DEA作为交易主体不仅需要满足上级电网侧负荷供应的要求，同时还需要实现底层不同发电形式的能源聚合，提高能源利用的效率，保证新能源消纳水平。本文所提出的博弈框架具体交易形式如图2所示。

根据区域能源聚合商的交易形式进行主从博弈，将博弈模型理解为一个双层优化问题：即上层经济优化问题与下层调度优化问题。在博弈模型中，电网作为博弈主体根据各DEA的报价并结合“最优消纳区间”给定市场出清电价以及各个DEA的火力发电与新能源发电的中标量；而各个DEA作为博弈从体进行独立决策，根据其他博弈从体的报价进行电力能源调度并选择最优报价策略，直到博弈双方达成Stackelberg均衡。

2 考虑最优消纳区间的主从博弈模型

2.1 DEA数学模型

如图2所示，各个DEA的下层发电形式主要包括风力发电、光伏发电及常规的火力发电。当已知某一时刻的各发电侧运行状态时，假定在下个时段内各能源生产商的响应状态保持不变，通过对下一时段内的响应进行分析，最终得到下一时段的最优出力组合。

2.1.1 常规火力发电

DEAi的火力发电成本可以用下式表示：

火力发电效益主要考虑如下：

2.1.2 新能源发电

本文主要考虑以风光为主的可再生能源，其发电过程中无燃料消耗，则运行成本模型中不考虑可再生能源的发电成本，只计及其运维成本，为了简化计算，本文将实际上网电量与该时段的总发电量的比值来表示各机组的并网比例。则DEAi的可再生能源运行成本如下：

新能源发电机组的发电效益主要考虑如下：

2.1.3 目标函数与约束条件

当已知DEAi在t时段的总出力时，需要对DEAi各类发电形式的电能进行调度，以实现其发电效益的优化，此时以DEAi在t时段的运行效益最大化为优化目标，其目标函数可以表示为

式中的第一项为DEAi在t时段向电网侧售电收入；第二项为t时段的发电总成本，即各类发电形式的成本之和。

在对上述目标进行优化时，需要满足电网侧安全可靠的相关约束条件，具体如下。

1）功率平衡约束。

式中：Pi,t为电网侧对于DEAi在t时段的期望传输功率。

2）常规火电机组运行约束。

2.2 电网侧数学模型

为了解决新能源消纳不合理的问题，本文基于“最优消纳区间”在电网的优化目标中加入新能源消纳惩罚成本，从而保证新能源的消纳水平更加合理。

电网侧是主从博弈模型中的主体部分，其目标是获得最低的单位购电价格保证电网安全稳定运行，并完成新能源的合理消纳。电网在t时段的购电总成本包括购电成本和新能源消纳惩罚成本：

式中：PDEAi,t为DEAi在t时段的总售电量； λt为整个交易系统在t时段的新能源消纳率； λA和λC分别为最优消纳区间的最小值和最大值；和分别为DEAi在t时段的新能源生产量和消纳量； αA和αC为新能源消纳的惩罚系数，均为正数。

所以电网侧的目标函数为：

在满足2.1.3节的相关约束条件外，电网侧在进行上述优化时，还需要满足以下约束：

式中：bt,min和bt,max分别为在t时段市场出清电价的允许最小值和最大值；为电网侧在t时段的要求负荷。

综上所述，博弈模型可由式（5）—（8）表示的DEA模型和式（14）—（16）表示的电网模型所构成。

3 求解算法

本文建立了考虑新能源最优消纳区间的双层优化模型，在上层优化中，电网侧根据不同的DEA报价确定经济成本最小的购电方案，实现新能源的合理消纳及电网的稳定运行；在下层优化中，各DEA根据电网给出的购电方案，对自身发电组合进行最优经济调度，以实现利益最大化目标。上层的经济优化结果是下层DEA进行优化调度的前提，而下层的优化调度方案则为上层优化提供了新的约束条件。上述的多层循环优化问题实质上构成了一个主从博弈模型。

3.1 上层经济优化问题

上层问题实际是为了在保障电力系统平稳运行并实现新能源合理消纳的前提下，确定各DEA的中标电量以及市场的出清电价，达成购电成本最低的目标。针对以上问题，本文采用基于交替方向乘子(Alternating Direction Method of Multipliers，ADMM)[12]的分布式优化算法进行求解。

上层经济优化问题解决后，电网便向各DEA下发中标电量以及市场出清电价。之后各DEA再根据电网的购电方案结合自身情况更新报价，直到电力市场达到Stackelberg均衡。

3.2 下层优化调度问题

下层优化调度问题的关键是要计算出DEAi针对其他DEA的最优报价策略，并且DEAi要根据其中标电量，在安全稳定的条件下对自身火力发电与新能源发电策略进行调整，以最低的成本满足电网需求从而获得最大收益。

根据以上分析，本文利用新型改进自适应遗传算法（New Improved Adaptive Genetic Algorithm，NIAGA）[13-14]求解此问题，是DEAi的博弈策略，分别代表DEAi的火力发电计划、光伏发电计划、风力发电计划以及向电网的报价策略。NIAGA算法中每一个种群个体表示DEAi的一种博弈策略，通过对种群的选择交叉变异可以获得DEAi的最优策略，从而实现其最高收益的目标。

3.3 主从博弈求解算法

本文利用如图3所示的流程对考虑双层优化问题的主从博弈模型进行求解。对于DEAi，根据其自身发电情况生成n个初始策略（Xi1,Xi2, ···,Xin），在其他DEA的策略保持不变的情况下（（Xij,X-i）,i=1,2,···n表示不包含DEAi的其余区域能源聚合商的策略），根据上层的经济优化模型可以得到DEAi的收益情况，再通过NIAGA算法最终得到DEAi的最优策略。对其他DEA重复以上步骤，求出所有DEA的最优策略。当所有DEA都不再改变自己的博弈策略时，则达到Stackelberg-Nash均衡，博弈结束。

4 算例分析

4.1 基础数据与约束条件

本文搭建含3个DEA的区域电网，仿真时间为用电高峰期11:00—12:00。各DEA的火力发电机组具体参数与约束条件如表1所示，新能源发电机组参数及第二日11：00电力预测如表2所示。据此计算得到3家区域能源聚合商的出力区间分别为DEA1[20.9, 60.9] MW、DEA2[16.4, 66.4] MW、DEA3[19.3, 49.3] MW，目标时段的电网侧期望DEA出力为Ptotal=77.0 MW，市场出清电价的设定范围为200～600元/（MW·h），各DEA的出力报价范围统一设为100～600元/（MW·h），最终的出清电价视为达成博弈均衡后的最高报价。本区域电网的最优消纳区间设为[0.90，0.95]；相应的惩罚系数 αA和αC分别为1600元与1500元。基于上述参数设置，对本文模型进行仿真分析。

表1 各DEA的火力发电机组参数Table 1 Parameters of thermal power generating sets of District Energy Aggregators (DEAs)

表2 第二日11:00时各DEA的运行状态参数Table 2 Operating state parameters of each DEA at 11:00 on the second day

4.2 案例对比分析

为了验证本文提出的双层优化主从博弈模型的有效性，以及考虑新能源“最优消纳区间”的必要性，特设立2个对比情形进行综合分析。两个对比情形均不进行主从博弈，每个DEA只根据历史交易情况进行一次报价，电网便根据一次报价情况决定中标量与出清电价。其中情形1要求实现新能源的100%消纳，而情形2则要求考虑新能源的“最优消纳区间”。两种不同情形下3个DEA的上报电价与各自的中标电量情况如图4、图5所示。

因为上述2种情形未进行博弈，所有DEA均只根据电力市场历史交易情况进行一次报价，根据图4、图5可知2种情况下的市场出清电价均为455.63元/MW·h，但考虑新能源“最优消纳区间”的影响后，情形2中3家DEA的中标电量均有提升。考虑新能源“最优消纳”区间时，各DEA的新能源消纳率如表3所示。

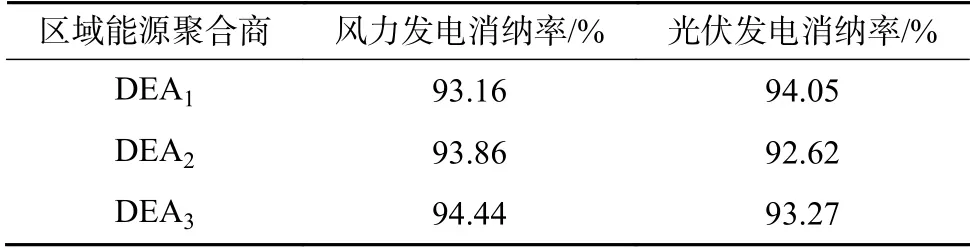
表3 未博弈最优消纳区间下的新能源消纳率Table 3 New energy resource accommodation rate under optimal accommodation interval having not participated in the game

4.3 模型求解分析

针对本文提出的主从博弈模型进行仿真求解，DEA与电网的博弈情况如图6所示，共进行13轮博弈达到Stackberg均衡。由图6可知，由于DEA2的单位发电成本较高，所以在博弈过程中DEA2的报价始终高于另外两家DEA。而3家DEA的最终上报电价与中标电量如图7所示。

结合图6、图7可知，该情形下电力市场出清电价为446.52元/MW·h，较前两种未博弈情形有所下降。此外，单位发电成本较低的DEA1与DEA3的中标电量要高于DEA2，说明发电成本越低的区域能源聚合商在电力市场中越具有竞争力。而该情形下各DEA的新能源消纳率如表4所示，参与主从博弈的情形下，保证在最优消纳区间内的3家区域能源聚合商的新能源消纳率分别提升了1.15%、1.32%、1.07%，这说明参与主从博弈能够促进新能源的最优消纳，优化新能源电力的投运使用。

根据以上分析，本文通过计算得到3种情形下的电力交易情况对比，结果如表5所示。对比可知较情形1而言，情形2考虑了新能源的最优消纳区间，虽然两种情形各区域能源聚合商的报价相同，但是情形2种各DEA的收益均有了提升，而且电网用更低的成本从区域能源聚合商中获得了更多的电量。这说明在一定条件下，追求新能源的完全消纳并不是最为经济高效的做法，适量的弃风弃光更加符合电网对区域能源聚合商的出力期望。

表5 不同情形下电力交易情况对比Table 5 Contrast of electricity transactions under different situations

情形3中DEA与电网进行了主从博弈，并考虑了新能源最优消纳区间的影响。经过多轮博弈，市场出清电价较其他两种情形有所下降，这将有利于电网降低自己的购电成本，而且各DEA的中标电量提升，各自的净利润也进一步提高。以上说明本文提出的双层优化主从博弈模型能够进一步提升电力市场整体效益，而且电网能够获得更加接近其需求的供电量，这将增强整个电力系统的调度运维能力，促进系统安全稳定运行。

5 结论

1）电力市场考虑新能源“最优消纳区间”能够提升社会的整体经济效益，目前而言新能源的全消纳并不是电网最期望的DEA出力方式。

2）双层优化主从博弈模型能够在保证系统安全稳定的前提下，实现博弈参与者的利益最大化，而且电力生产成本越低的DEA在电力市场的博弈中越具有竞争力。

3）该模型还能促进“最优消纳区间”内新能源消纳率的进一步提升，提升比例不低于1.07%，有利于帮助新能源消纳达到最优状态。

本文所做研究以DEA的运行模式为基础，可为区域电力市场提供运营模式借鉴。但并未考虑新能源发电机组的发电量预测误差，以及储能电站对博弈过程的影响，后续研究中将建立更贴近实际的优化调度与电价博弈模型。