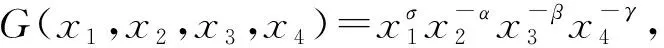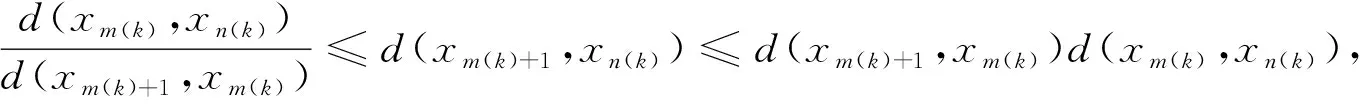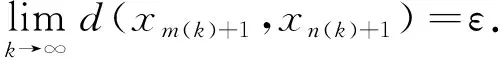乘积度量空间上一类隐式压缩映射的唯一不动点

朴 勇 杰

(延边大学 理学院 数学系, 吉林 延吉 133002)

Banach压缩原理[1]即Banach不动点定理, 是不动点理论中最基本、 最简单形式的定理, 在数学及其他领域应用广泛. 目前, 关于Banach不动点定理在各类不同广义度量空间上的推广和改进已有很多成果. Bashirov等[2]通过引入乘积度量空间的概念, 给出了一些基本性质； Florack等[3]和Bashirov等[4]在乘积度量空间上进一步研究了一些其他性质; Özavar等[5]在乘积度量空间上通过引进乘积压缩映射的概念, 给出了若干个乘积压缩映射的不动点存在定理.

设(X,d)是乘积度量空间.映射f:X→X称为乘积压缩映射[5]是指存在λ∈[0,1), 使得

d(fx,fy)≤[d(x,y)]λ, ∀x,y∈X.

(1)

文献[5]给出了如下形式的乘积度量空间上Banach型不动点定理:

定理1[5]完备的乘积度量空间(X,d)上的任何乘积压缩映射f必有唯一不动点.

文献[6]通过引进一个如下的三元实函数类, 得到了一个唯一不动点定理.

σ∈Σ当且仅当σ: [1,∞)3→[0,∞)满足下列条件：

(i)σσ关于每个变量连续;

(ii)σ存在k∈[0,1), 使得当x,y∈[1,∞)且满足x≤σ(y,y,x)或x≤σ(y,x,y)或x≤σ(x,y,y)时,x≤yk成立.

定理2[6]设(X,d)是完备的乘积度量空间, 且f:X→X为映射.如果对任何x,y∈X, 均有

d(fx,fy)≤σ(d(x,y),d(x,fx),d(y,fy)),

(2)

则f在X中存在唯一不动点, 其中σ∈Σ.

文献[6]对定理2的证明首先任意给定x0∈X, 其次构造一个序列{xn}使其满足xn+1=fxn, 然后证明该序列满足乘积Cauchy准则, 并证明{xn}是乘积Cauchy序列, 最后证明该序列的极限正是f的唯一不动点.证明过程中最关键的一步是说明{xn}是乘积Cauchy序列.

本文通过引进四元函数类, 并在乘积度量空间上建立隐式压缩条件, 给出一个不动点定理.本文主要结果证明中所涉及的序列{xn}未必满足乘积Cauchy准则, 因此需采用另一种方法证明{xn}是乘积Cauchy序列, 从而说明唯一不动点的存在性.因此本文的结果推广并改进了文献[6]及其相关结果.

定义1[2]设X是非空集合, 映射d:X×X→[0,∞)称为X上的乘积度量是指d满足:

1) 对任何x,y∈X,d(x,y)≥1且d(x,y)=1⟺x=y;

2) 对任何x,y∈X,d(x,y)=d(y,x);

3) 对任何x,y,z∈X,d(x,z)≤d(x,y)d(y,z)(乘积三角不等式).

此时称(X,d)为乘积度量空间.

关于乘积度量空间的实例可参见文献[5,7-11].

例1[7,9]设X=, 定义d(x,y)=e|x-y|(∀x,y∈X), 则(,d)是乘积度量空间.

定义2[2]设(X,d)是乘积度量空间, {xn}是X中序列且x∈X.若对任何积性开球Bε(x)={y∈X|d(x,y)<ε},ε>1, 均存在自然数N, 使得当n>N时,xn∈Bε(x)成立, 则称序列{xn}乘积收敛于x, 记为xn→x(n→∞).

引理1[5]设(X,d)是乘积度量空间, {xn}是X中序列且x∈X, 则

xn→x(n→∞)⟺d(xn,x)→1(n→∞).

定义3[5]设(X,d)是乘积度量空间, {xn}是X中序列.若对任何ε>1, 均存在自然数N, 使得当n,m>N时,d(xn,xm)<ε成立, 则称序列 {xn}为乘积Cauchy序列.

引理2[5]设(X,d)是乘积度量空间, {xn}是X中序列, 则{xn}是乘积Cauchy序列当且仅当d(xm,xn)→1(m,n→∞).

定义4[5]如果乘积度量空间(X,d)中的每个乘积Cauchy序列都是乘积收敛的, 则称(X,d)是完备的.

引理3[5]设(X,d)是乘积度量空间, {xn}和{yn}是X中的两个序列且x,y∈X, 则

xn→x,yn→y(n→∞)⟹d(xn,yn)→d(x,y)(n→∞).

下面引进一个函数类.

定义5G∈G ⟺G: [1,∞)4→[0, ∞)满足下列条件：

(i)GG关于每个变元是连续的;

(ii)G对任何x,y∈[1,∞), 当x≠y且G(x,y,y,x)≤1或G(x,x,y,y)≤1时,x

(iii)Gx>1当且仅当G(x,x,x,x)>1.

注1定义5中未要求存在常数k∈[0,1), 使得在满足某种条件下x≤yk成立, 因此在一般情况下无法推出乘积Cauchy准则.

G(x,x,x,x)=xσ-α-β-γ>1⟺x>1,

于是(iii)G也成立.

定理3设(X,d)是完备的乘积度量空间且f:X→X为映射.如果存在G∈G, 使得对任何x,y∈X, 均有

G(d(fx,fy),d(x,y),d(x,fx),d(y,fy))≤1,

(3)

则f在X中存在唯一不动点.

证明: 任取x0∈X, 根据xn+1=fxn(n=0,1,2,…)构造一个序列{xn}.如果存在某一非负整数N, 使得d(xN,xN+1)=1, 则xN=fxN, 因此xN是f的一个不动点.于是假设对任何n=0,1,2,…,d(xn,xn+1)>1.

对任何n=1,2,…, 根据式(3)得

G(d(fxn-1,fxn),d(xn-1,xn),d(xn-1,fxn-1),d(xn,fxn))≤1,

整理得

G(d(xn,xn+1),d(xn-1,xn),d(xn-1,xn),d(xn,xn+1))≤1.

(4)

如果存在N, 使得d(xN-1,xN)=d(xN,xN+1), 则由(iii)G得

G(d(xN,xN+1),d(xN-1,xN),d(xN-1,xN),d(xN,xN+1))>1,

与式(4)矛盾, 于是对任何n, 均有d(xn-1,xn)≠d(xn,xn+1).根据(ii)G, 由式(4)得

d(xn,xn+1)

(5)

在式(4)两边取n→∞, 根据(i)G得

G(u,u,u,u)≤1,

于是由(iii)G得u=1, 即

假设{xn}不是乘积Cauchy序列, 则存在实数ε>1, 使得对任何自然数k, 均存在两个自然数m(k)和n(k), 使得m(k)>n(k), 且满足

d(xm(k),xn(k))>ε,d(xm(k)-1,xn(k))≤ε.

(6)

由式(6)和定义1中3)可得

ε≤d(xm(k),xn(k))≤d(xm(k),xm(k)-1)d(xm(k)-1,xn(k))≤d(xm(k),xm(k)-1)ε.

(7)

对式(7)两边取k→∞并利用u=1可得

(8)

再根据定义1中3)得

(9)

(10)

在式(9)和式(10)两边取k→∞, 并根据u=1和式(8)可得

(11)

类似地, 根据u=1和式(11), 由

得

(12)

对任何k, 根据式(3)得

G(d(fxm(k),fxn(k)),d(xm(k),xn(k)),d(xm(k),fxm(k)),d(xn(k),fxn(k)))≤1,

整理得

G(d(xm(k)+1,xn(k)+1),d(xm(k),xn(k)),d(xm(k),xm(k)+1),d(xn(k),xn(k)+1))≤1.

(13)

对式(13)两边取k→∞并结合(8),(12)及u=1和(i)G可得

G(ε,ε,1,1)≤1.

于是由(ii)G得ε=1, 与ε>1矛盾.因此{xn}是乘积Cauchy序列.根据(X,d)的完备性知, 存在x*∈X, 使得d(xn,x*)→1(n→∞).

对任何n, 根据式(3)得

G(d(fxn,fx*),d(xn,x*),d(xn,fxn),d(x*,fx*))≤1,

(14)

整理式(14)并对其两边取n→∞, 根据(i)G及引理3可得

G(d(x*,fx*),1,1,d(x*,fx*))≤1.

如果d(x*,fx*)>1, 则d(x*,fx*)≠1且根据(ii)G得到d(x*,fx*)<1, 矛盾, 于是必有d(x*,fx*)=1, 从而fx*=x*, 即x*是f的一个不动点.如果y*也是f的不动点, 则根据式(3)得

G(d(x*,y*),d(x*,y*),1,1)=G(d(fx*,fy*),d(x*,y*),d(x*,fx*),d(y*,fy*))≤1,

于是必有d(x*,y*)=1, 即x*=y*, 因此f有唯一不动点x*.

根据定理3和例3可得如下结果.

定理4设(X,d)是完备的乘积度量空间, 且f:X→X为映射.如果对任何x,y∈X, 均有

[d(fx,fy)]σ≤[max{d(x,y),d(x,fx),d(y,fy)}]k,

则f在X中存在唯一不动点, 其中σ>k.

注2如果在定理4中取σ>k>0, 则定理4即为文献[6]中的定理4; 如果k<σ<0, 则定理4变为膨胀型映射的Ciric型不动点定理; 如果k=0, 则对任何x,y∈X,d(fx,fy)=1, 即fx=fy, 因此f是一个常值x0∈X的映射, 于是x0即为f的唯一不动点.

根据定理3和例4可得如下形式的不动点定理.

定理5设(X,d)是完备的乘积度量空间, 且f:X→X为映射.如果对任何x,y∈X, 均有

d(fx,fy)[1+max{d(x,y),d(y,fy)}d(x,fx)]≤1+d(x,y)d(x,fx)d(y,fy),

(15)

则f在X中有唯一不动点.

例5设X={0,2,5}, 考虑d(x,y)=e|x-y|(∀x,y∈X), 则由例1知(X,d)是完备的乘积度量空间.定义f:X→X为f0=f2=0,f5=2(下面将式(15)不等号左边用Δ表示, 右边用表示).

当x,y∈{0,2}及x=y=5时,d(fx,fy)=1, 于是

Δ=[1+max{d(x,y),d(y,fy)}d(x,fx)]≤1+d(x,y)d(x,fx)d(y,fy)=;

当x=0,y=5时,

当x=2,y=5时,

于是(X,d),f满足定理5的所有条件, 因此f有唯一不动点0.