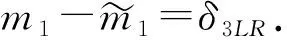3-李-Rinehart Color代数的上同调与形变

腾 文, 游泰杰

(1. 贵州师范大学 数学科学学院, 贵阳 550025; 2. 贵州财经大学 数统学院, 贵阳 550025)

Huebschmann[1-4]首次引入了李-Rinehart代数的概念, 并对李-Rinehart代数在李代数胚上的作用进行了系统研究. 李color代数是李代数和李超代数的推广, 目前已有很多研究成果, 例如: Scheunert等[5-6]通过研究李color代数, 得到了PBW定理和Ado定理, 并引入其上同调理论; Chen等[7]研究了李color代数的广义导子结构; Yuan[8]和Abdaoui等[9]相继研究了Hom-李color代数的上同调、 形变及其相关性质； Piontkovski等[10]引入了3维李color代数的上同调理论; 白瑞蒲等[11]引入了3-李-Rinehart代数的概念, 并讨论了其基本结构、 作用和交叉模； Hassine等[12]引入了3-李-Rinehart超代数的概念, 并研究了其上同调和结构. 受上述研究启发, 本文引入3-李-Rinehart color代数的概念, 通过系数模讨论3-李-Rinehart color代数的上同调复形, 并刻画3-李-Rinehart color代数的形变.

1 预备知识

设K是特征为0的代数闭域,R表示有单位元的交换环,+表示所有非负整数集.如无特殊声明, 所有的模均在环R上, 所有的线性映射均指R-线性映射.

定义1[5]设Γ为Abel群, 对于映射ε:Γ×Γ→K*, 如果对任意的α,β,γ∈Γ, 均满足下列等式:

则称ε为Γ的斜对称双特征标.

[x,y,z]=-ε(x,y)[y,x,z], [x,y,z]=-ε(y,z)[x,z,y] (斜ε-对称性),

(1)

定义3设(L,[·,·,·],ε)是3-李color代数,V是Γ-阶化向量空间, 如果偶双线性映射ρ:L∧L→gl(V), 满足对任意的xi∈H(L)(1≤i≤4), 下列等式成立:

则称(V,ρ)为L的一个表示,V为L-模.

定义ad:L∧L→gl(L), adx,y(z)=[x,y,z].由式(2)可见, (L,ad)是3-李color代数的一个表示, 称为L的伴随表示.

2 主要结果

下面讨论3-李-Rinehart color代数的上链复形和上同调, 引入3-李-Rinehart color代数的概念. 进一步讨论3-李-Rinehart color代数的上同调中1-余循环和2-余循环的关系, 并通过上同调理论刻画3-李-Rinehart color代数的形变.

定义4设一个A上的3-李-Rinehart color代数是一个五元组(L,A,[·,·,·],ρ,ε), 其中ε为Γ上的斜对称双特征标,A是ε-交换结合阶化代数,L是一个A-模, [·,·,·]:L×L×L→L是斜ε-对称偶三线性映射,R-映射ρ:L×L→Der(A)满足下列条件:

1) (L,[·,·,·],ε)是3-李color代数;

2) (A,ρ)是(L,[·,·,·],ε)的一个表示;

3) 对所有的x,y∈H(L),a∈H(A), 均有

ρ(ax,y)=ε(a,x)ρ(x,ay)=aρ(x,y)；

(5)

4) 相容性:

[x,y,az]=ε(a,x+y)a[x,y,z]+ρ(x,y)az, ∀x,y,z∈H(L),a∈H(A).

(6)

定义5设(L,A,[·,·,·]L,ρ,ε)和(L′,A′,[·,·,·]L′,ρ′,ε)是两个3-李-Rinehart color代数,g:A→A′和f:L→L′是两个R-代数同态, 对∀x,y∈H(L),a∈H(A), 满足下列条件:

1)f(ax)=g(a)f(x);

2)g(ρ(x,y)(a))=ρ′(f(x),f(y))(g(a)).

则称(g,f)是3-李-Rinehart color代数的同态.

定义6设M是一个A-模,ψ:L⊗L→End(M)是偶双线性映射.如果下列条件成立:

1)ψ是(L,[·,·,·],ε)在M上的一个表示;

2) 对所有的a∈H(A),x,y∈H(L), 均有ψ(a·x,y)=ε(a,x)ψ(x,a·y)=a·ψ(x,y);

3) 对所有的a∈H(A),x,y∈H(L),m∈M, 均有

ψ(x,y)(a·m)=ε(a,x+y)a·ψ(x,y)(m)+ρ(x,y)(a)m.

则称序对(M,ψ)为3-李-Rinehart color代数(L,A,[·,·,·],ρ,ε)的左模.

例1序对(L,ad)是L上的一个左模, 称为(L,A,[·,·,·],ρ,ε)的伴随表示.

命题1设(L,A,[·,·,·],ρ,ε)是3-李-Rinehart color代数, 则(M,ψ)是(L,A,[·,·,·],ρ,ε)左模的充要条件是(L⊕M,A,[·,·,·]L⊕M,ρL⊕M,ε)是3-李-Rinehart color代数, 其中[·,·,·]L⊕M,ρL⊕M的定义如下: 对任意的x1,x2,x3∈H(L),m1,m2,m3∈M, 均有

ρL⊕M: (L⊕M)⊗(L⊕M)→Der(A),ρL⊕M(x1+m1,x2+m2)∶=ρ(x1,x2).

证明: 必要性.因为L和M是A-模, 则∀a∈A,x∈L,m∈M, 有a(x+m)=ax+am, 于是L⊕M也是一个A-模.如果(M,ψ)是(L,A,[·,·,·],ρ,ε)上的一个左模, 则(L⊕M,[·,·,·]L⊕M,ε)是3-李color代数.显然ρL⊕M是3-李color代数(L⊕M,[·,·,·]L⊕M,ε)在A上的一个表示.

对任意的x1,x2,x3∈H(L),m1,m2,m3∈H(M),a∈ H(A), 有

进一步, 有

类似可得

ρL⊕M(a(x1+m1),x2+m2)=aρL⊕M(x1+m1,x2+m2).

因此(L⊕M,A,[·,·,·]L⊕M,ρL⊕M,ε)是3-李-Rinehart color代数.

充分性类似可证.证毕.

设(M,ψ)是3-李-Rinehart color代数(L⊕M,A,[·,·,·]L⊕M,ρL⊕M,ε)的一个左模, 用Cn(L,M)表示所有线性映射f: ∧2L⊗…⊗∧2L∧L→M生成的空间, 其中f满足下列条件:

1)f(x1,…,xi,xi+1,…,x2n,x2n+1)=-ε(xi,xi+1)f(x1,…,xi+1,xi,…,x2n,x2n+1);

2)f(x1,…,axi,…,x2n+1)=-ε(a,x1+…xi-1+f)af(x1,…,xi,…,x2n+1).

下面考虑R-模的+-阶化空间:线性映射δ3LR:Cn-1(L,M)→Cn(L,M)定义为

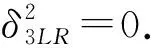
证明: 设齐次元f∈Cn-1(L,M), 显然δ3LRf是斜ε-对称.对所有的x1,x2,…,x2n+1∈H(L),a∈H(A),i<2n-1, 均有

利用定义4和式(6), 有

δ3LRf(x1,…,axi,…,x2n+1)=ε(a,x1+…+xi-1+f)aδ3LRf(x1,…,xi,…,x2n+1).

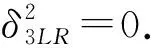
由上述性质可知, (C*(L,M),δ3LR)是上链复形.因此, 上链复形的上同调可定义为3-李-Rinehart color代数(L,A,[·,·,·],ρ,ε)的上同调空间, 其系数为(M,ψ), 记为H*(L,M).

则称v为与ψ相关联的1-余循环.

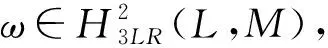
则称ω为与ψ相关联的2-余循环.

设(L,[·,·],ε)为李-color代数,τ:L→K是偶线性型.如果τ([·,·])=0, 则称τ是L的阶化迹.对于x1,x2,x3∈H(L), 定义3-元括积为

[x1,x2,x3]τ=τ(x1)[x2,x3]-ε(x1,x2)τ(x2)[x1,x3]+ε(x3,x1+x2)τ(x3)[x1,x2].

定理2设(L,[·,·],ε)为李-color代数,τ是L的阶化迹, 则(L,[·,·,·]τ,ε)是3-李-color代数.

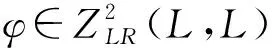
τ(x)τ(φ(y,z))-ε(x,y)τ(y)τ(φ(x,z))+ε(z,x+y)τ(z)τ(φ(x,y))=0.

线性映射φ: ⊗3L→L定义为

φ(x,y,z)=τ(x)φ(y,z)-ε(x,y)τ(y)φ(x,z)+ε(z,x+y)τ(z)φ(x,y).

则φ是由3-李-Rinehart color代数(L,A,[·,·,·]τ,ρτ,ε)诱导的一个2-余循环.

类似地, 有

另一方面, 设x1,x2,y1,y2,z∈H(L), 则

因为对所有的x,y,z∈H(L), 均有

τ(x)τ(φ(y,z))-ε(x,y)τ(y)τ(φ(x,z))+ε(z,x+y)τ(z)τ(φ(x,y))=0,

因此δ3LRφ=0.证毕.

由定理3可得以下推论.

ψ(x,y,z)=τ(x)φ(y,z)-ε(x,y)τ(y)φ(x,z)+ε(z,x+y)τ(z)φ(x,y)

是由3-李-Rinehart color代数诱导的一个2-余循环.

定理4李-Rinehart color代数(L,A,[·,·],μ,ε)标量上同调的每个1-余循环都是由3-李-Rinehart color代数(L,A,[·,·,·]τ,ρτ,ε)标量上同调诱导的一个1-余循环.

引理1设φ∈C1(L,R), 则对所有的x,y,z∈L, 均有

δ3LRφ(x,y,z)=τ(x)δLRφ(y,z)-ε(x,y)τ(y)δLRφ(x,z)+ε(z,x+y)τ(z)δLRφ(x,y).

证明: 设φ∈C1(L,R),x,y,z∈L, 则

证毕.

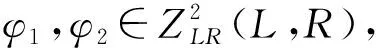
ψi(x,y,z)=τ(x)φi(y,z)-ε(x,y)τ(y)φi(x,z)+ε(z,x+y)τ(z)φi(x,y),i=1,2.

因此ψ1,ψ2在相同的上同调类.证毕.

下面讨论3-李-Rinehart color代数的形变.设K[[t]]是以t为变量的形式幂级数环.

定义9设(L,A,[·,·,·],ρ,ε)为3-李-Rinehart color代数, 则L的形变是一组幂级数：

其中每个mi是偶三线性映射,m0=[·,·,·], ∀x,y,z,u,v∈H(L),a∈H(A), 满足下列条件:

ρ(ax,y)=ε(a,x)ρ(x,ay)=aρ(x,y),

[x,y,az]t=ε(a,x+y)a[x,y,z]t+ρ(x,y)az.

设[·,·,·]t是[·,·,·]的一个形变, 则

对比tn(n≥0)的系数, 可得下列方程:

定义103-上链m1称为形变[·,·,·]t的微小形变.一般地, 如果mi=0(1≤i≤n-1),mn为非零上链, 则mn称为形变[·,·,·]t的n-微小形变.

定义11如果存在L[[t]]-模形式同构

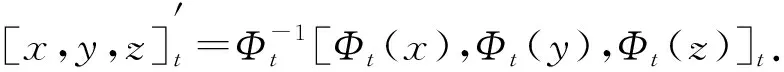
定理5微小形变[·,·,·]t的上同调类由[·,·,·]t的等价类决定.

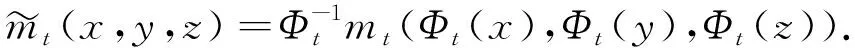
(7)

对比方程(7)两边t的系数, 有