一般线性李超代数在广义Witt李超代数中的中心化子

茅 丹, 郑克礼

(东北林业大学 理学院, 哈尔滨 150040)

李超代数[1]在物理学中用于研究超对称现象. Wess等[2]应用超对称理论提出了四维超对称理论. 目前, 关于非模李超代数的研究已趋于完善, 但模李超代数的研究还处于发展阶段[3]. 中心化子的概念源于群结构的研究[4], 李超代数是由李超群线性化得到的, 所以也存在中心化子. 目前, 关于李超代数中心化子的研究已得到广泛关注. 文献[5]研究了gl(0,2)在广义Witt李超代数上的中心化子; 文献[6]研究了sl(0,3)在广义Witt李超代数上的中心化子. 由于用伴随表示去体现一个李超代数, 能将李超代数视为其子代数的一个自然模, 所以中心化子能等价地视为零维上同调群.

本文受文献[7]中求解三阶矩阵李超代数中心化子的启发, 利用同调方法讨论一般线性李超代数gl(m,n)在广义Witt李超代数W上的中心化子, 通过计算分别给出gl(m,n)(m=1,2,…,a;n=1,2,…,b)在W上的中心化子,gl(m,0)(m=1,2,…,a)在W上的中心化子, 以及gl(0,n)(n=1,2,…,b)在W上的中心化子.

1 预备知识

根据文献[8], 素特征域F上的广义Witt李超代数结构为W=w⊕ω, 其中

这里Y0={1,2,…,a},Y1={1,2,…,b}.易知李超代数gl(m,n),gl(m,0),gl(0,n)的标准基分别为{XrDs,Xrdv,ζqDs,ζqdv},{XrDs},{ζqdv}(r,s=1,2,…,m;q,v=1,2,…,n).

定义1[9]设L是李代数,A是L-模,Hn(L,A)=Kerδn/(Imδn-1)称为L的系数在其模A上的n维上同调.

引理1[9]对任意的L-模A,H0(L,A)={a∈A|x·a=0,x∈L}.

2 中心化子CW(gl(m,n))

2.1 零维上同调H0(gl(m,n),w)

命题1gl(m,n)在w0上的零维上同调为

证明： 根据定义w0=〈X(α)ζuDk||α|+|u|=1,k∈Y0〉, 设存在

满足[gl(m,n),f]=0, 其中ck,gjk∈F, |α|=1.则:

1) 当X(α)为X1,X2,…,Xm中任意一个时, 有

其中:r,s=1,2,…,m;q,v=1,2,…,n.因为D1,D2,…,Da是线性无关的, 所以由上述等式可得ck=0,gvk=0(v=1,2,…,n),gjr=0(r=1,2,…,m).此时结果为

〈ζjDk|j∈Y1{1,2,…,n},k∈Y0{1,2,…,m}〉.

2) 当X(α)不为X1,X2,…,Xm中任意一个, 且k∈Y0{1,2,…,m}时, 有

[XrDs,f]=0, [ζqDs,f]=0, [Xrdv,f]=0, [ζqdv,f]=0,

其中:r,s=1,2,…,m;q,v=1,2,…,n.所以此时结果为

〈X(α)-〈i〉Dk||α|=2,i∈{1,2,…,m},k∈Y0{1,2,…,m}〉.

综上, 结论得证.

命题2gl(m,n)在w1上的零维上同调为

证明： 由定义知,w1=〈X(α)ζuDk||α|+|u|=2,k∈Y0〉.可设

满足[gl(m,n),f]=0, 其中cjk,gk,hijk∈F, |α|=1, |β|=2.则:

1) 当X(α)为X1,X2,…,Xm中任意一个,X(β)含X1,X2,…,Xm中任意一个时, 由

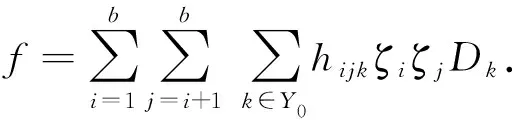
从而hijr=0(r=1,2,…,m),hvjk=0(v=1,2,…,n).当k∈Y0{1,2,…,m},i,j均不取1,2,…,n时, [gl(m,n),f]=0.此时结果为

〈ζu-〈j〉Dk||u|=3,j∈{1,2,…,n},k∈Y0{1,2,…,m}〉.

2) 当X(α)ζjDk中的X(α)不为X1,X2,…,Xm中任意一个,j∈Y1{1,2,…,n},k∈Y0{1,2,…,m}, 且X(β)Dk中X(β)不含X1,X2,…,Xm中任意一个,k∈Y0{1,2,…,m}时, [gl(m,n),f]=0.此时结果为

综合1),2), 结论得证.

命题3gl(m,n)在w2上的零维上同调为

证明： 由定义知,w2=〈X(α)ζuDk||α|+|u|=3,k∈Y0〉.可设存在

满足[gl(m,n),f]=0, 其中cjk,gk,hijk,mijlk∈F, |α|=1, |β|=2, |γ|=3.则:

1) 当X(α)为X1,X2,…,Xm中任意一个, 且X(β),X(γ)含有X1,X2,…,Xm中任一个时, 有

又因为D1,D2,…,Da是线性无关的, 所以hijk=cjk=gk=0.再根据

[XrDs,f]=0, [Xrdv,f]=0, [ζqdv,f]=0,

可得mijlr=0(r=1,2,…,m),mvjlk=0(r=1,2,…,n).其中:r,s=1,2,…,m;q,v=1,2,…,n.当ζiζjζlDk中i,j,l均不等于1,2,…,n, 且k∈Y0{1,2,…,m}时, 有[gl(m,n),ζiζjζlDk]=0.此时结果为

〈ζu-〈j〉Dk||u|=4,j∈{1,2,…,n},k∈Y0{1,2,…,m}〉.

2) 当X(α)不为X1,X2,…,Xm中任意一个,X(β),X(γ)不含有X1,X2,…,Xm中任意一个, 且{u}中不含1,2,…,n,k∈Y0{1,2,…,m}时, 有[gl(m,n),f]=0.此时结果为

综合1),2), 结论得证.

由命题1～命题3易得：

推论1对于wt(t≥1),H0(gl(m,n),wt)是t+2项的直和, 即

结合命题1～命题3以及推论1易得:

定理1gl(m,n)在w上的零维上同调为

2.2 零维上同调H0(gl(m,n),ω)

命题4gl(m,n)在ω0上的零维上同调为

证明： 由定义知,ω0=〈X(α)ζudl||α|+|u|=1,l∈Y1〉.设存在

满足[gl(m,n),f]=0, 其中cl,gjl∈F, |α|=1.则:

1) 当X(α)为X1,X2,…,Xm中任意一个时, 由

以及d1,d2,…,db线性无关, 可得cl=0,gvl=giq=0(v,q=1,2,…,n).此时结果为〈ζjdl|j,l∈Y1{1,2,…,n}〉.

[XrDs,f]=0, [Xrdv,f]=0, [ζqDs,f]=0, [ζqdv,f]=0.

此时结果为〈X(α)-〈i〉dl||α|=2,i∈{1,2,…,m},l∈Y1{1,2,…,n}〉.

综合1),2), 结论得证.

命题5gl(m,n)在ω1上的零维上同调为

证明： 由定义知,ω1=〈X(α)ζudl||α|+|u|=2,l∈Y1〉.设存在

满足[gl(m,n),f]=0, 其中cl,gjl,hijl∈F, |α|=1, |β|=2.则:

1) 当X(α)为X1,X2,…,Xm中任意一个, 且X(β)含有X1,X2,…,Xm中任一个时, 由

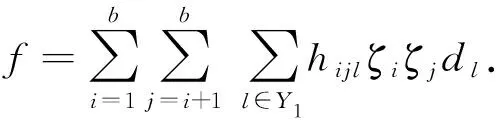
可知,hvjl=0(v=1,2,…,n).当ζiζjdl中的i,j都不等于1,2,…,n时, 对l∈Y1{1,2,…,n}有[gl(m,n),ζiζjdl]=0.此时结果为

〈ζu-〈j〉dl||u|=3,j∈{1,2,…,n},l∈Y1{1,2,…,n}〉.

2) 当X(α)ζjdl中的X(α)不为X1,X2,…,Xm中任意一个,j,l∈Y1{1,2,…,n}, 且X(β)dl中的X(β)不含有X1,X2,…,Xm中任意一个,l∈Y1{1,2,…,n}时, 有[gl(m,n),f]=0.此时结果为

综合1),2), 结论得证.

命题6gl(m,n)在ω2上的零维上同调为

证明： 由定义知,ω2=〈X(α)ζudl||α|+|u|=3,l∈Y1〉.可设存在

满足[gl(m,n),f]=0, 其中gl,cjl,hijl,mijzl∈F, |α|=1, |β|=2, |γ|=3.则:

1) 当X(α)为X1,X2,…,Xm中任意一个, 且X(β),X(γ)含有X1,X2,…,Xm中任一个时, 由

可得hijl=cjl=gl=0, 其中:r,s=1,2,…,m;d1,d2,…,db线性无关.此时, 有

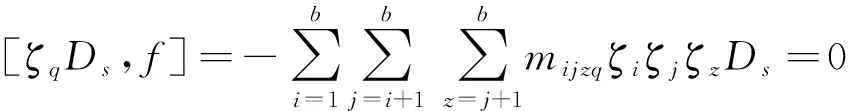
得mvjzl=mijzq=0(v,q=1,2,…,n).当ζiζjζzdl中的i,j,z均不取1,2,…,n中任意一个数时, 对l∈Y1{1,2,…,n}, 有[gl(m,n),ζiζjζzdl]=0.此时结果为

〈ζu-〈j〉dl||u|=4,j∈{1,2,…,n},l∈Y1{1,2,…,n}〉.

2) 当X(α)ζiζjdl中的X(α)不取X1,X2,…,Xm中任意一个,i,j,l∈Y1{1,2,…,n},X(β)ζjdl中的X(β)不含X1,X2,…,Xm中任意一个,j,l∈Y1{1,2,…,n}, 且X(γ)dl中的X(γ)不取X1,X2,…,Xm中任意一个,l∈Y1{1,2,…,n}时, [gl(m,n),f]=0.此时结果为

综合1),2), 结论得证.

由命题4～命题6易得：

推论2对于ωt(t≥1),H0(gl(m,n),ωt)是t+2项的直和, 即

结合命题4～命题6以及推论2易得:

定理2gl(m,n)在ω上的零维上同调为

综上可得:

定理3gl(m,n)(1≤m≤a, 1≤n≤b)在W上的中心化子为

3 中心化子CW(gl(m,0))

3.1 零维上同调H0(gl(m,0),w)

命题7gl(m,0)在w0上的零维上同调为

证明： 由定义知,w0=〈X(α)ζuDk||α|+|u|=1,k∈Y0〉.设存在

满足[gl(m,0),f]=0, 其中ck,gji∈F, |α|=1.则:

1) 当X(α)等于X1,X2,…,Xm中某一个时, 由

以及D1,D2,…,Da线性无关, 可得ck=0,gjr=0(r=1,2,…,m).此时结果为

〈ζuDk||u|=1,k∈Y0{1,2,…,m}〉.

再根据

可得ck=0(k∈Y0{r}),gjr=0(r=1,2,…,m).此时结果为〈X1D1+…+XmDm〉.因此在1)中得到的结果为

〈X1D1+…+XmDm〉⊕〈ζuDk||u|=1,k∈Y0{1,2,…,m}〉.

2) 当X(α)不等于X1,X2,…,Xm中任意一个,k∈Y0{1,2,…,m}时, 有[gl(m,0),f]=0.此时结果为〈X(α)-〈i〉Dk||α|=2,i∈{1,2,…,m},k∈Y0{1,2,…,m}〉.

综合1),2), 结论得证.

仿照命题7的证明, 易得:

命题8gl(m,0)在w1上的零维上同调为

由命题7和命题8易得:

推论3对于wt(t≥0),H0(gl(m,0),wt)是2t+3项的直和, 即

由命题7、 命题8以及推论3易得:

3.2 零维上同调H0(gl(m,0),ω)

与上述方法同理可得如下结论：

定理5gl(m,0)在ω上的零维上同调为

其中

H0(gl(m,0),ω0)=〈X(α)-〈i〉dl||α|=2,i∈{1,2,…,m},l∈Y1〉⊕〈ζjdl|j,l∈Y1〉,

综上, 可得gl(m,0)(1≤m≤a)在W上的中心化子：

定理6gl(m,0)在W上的中心化子为

4 中心化子CW(gl(0,n))

与上述方法同理对gl(m,0)(m=1,2,…,a)在W上讨论中心化子, 可得：

定理7gl(0,n)(n=1,2,…,b)在W上的中心化子为

其中

H0(gl(0,n),w0)=〈X(α)Dk||α|=1,k∈Y0〉⊕〈ζu-〈j〉Dk||u|=2,j∈{1,2,…,n},k∈Y0〉,