计及电能质量影响的10 kV配电网损耗计算模型及其实验验证

李琼林，刘书铭，温佳静，王 毅，代双寅，谭甜源，刘开培

（1. 国网河南省电力公司电力科学研究院，河南 郑州 450000；2. 武汉大学电气与自动化学院，湖北 武汉 430072）

0 引言

传统的配电网损耗计算是在理想的供电环境下进行的，当配电网存在电能质量扰动时会产生较大的计算误差，且电能质量扰动越严重误差越大。近年来，各种新型用电设备、轨道交通、分布式电源等干扰源负荷持续增长，其非线性、冲击性和不平衡在电力生产和用电过程中会对配电网产生严重污染，如波形畸变、三相电压不平衡、电压波动和闪变等，使得配电网电能质量日益恶化，进一步增加配电网损耗［1-4］。因此，在进行10 kV 配电网线损计算时如何计及电能质量因素，提高10 kV 配电网损耗计算的准确性与合理性，对于电力行业进一步的节能降损具有十分重要的意义。

目前国内外的研究大部分仅分析了单一电能质量扰动对低压配电网损耗的影响，主要集中在谐波和三相电流不平衡的分析及相应的治理措施方面。文献［5-6］以hR（h为谐波次数，R为直流电阻）等效h次谐波电阻，此种简化模型能够体现谐波附加损耗随谐波次数的变化趋势，但该模型未考虑线路材料等因素对谐波电阻的影响，针对不同型号的线路计算误差较大，难以满足谐波附加损耗计算精度。文献［7］提出了一种考虑集肤效应影响的低压配电线路谐波电阻参数辨识算法，并采用实测运行数据完成谐波电阻参数辨识，得到了线路谐波电阻模型，但该方法依托于实测数据，计算量大，且没有给出谐波电阻与谐波次数之间的量化关系公式。文献［8］参考IEEE Std C57.110 标准［9］中变压器绕组涡流谐波损耗因子和杂散谐波损耗因子的计算方法得出绕组电阻谐波损耗因子的计算公式，并利用以上3 个因子计算变压器负载谐波损耗，该方法模型较为简单，易于实现。文献［10］以A、B、C 相的电流幅值不平衡度作为指标，计算配电变压器（下文称配变）和线路的三相电流不平衡系数，从而推导出低压配电网中的三相电流不平衡附加损耗，但是该方法没有考虑相角不平衡，不够精确。文献［11］对变压器中绕组的电磁场进行了分析，利用坡印亭矢量法得出各层绕组的损耗计算公式，由此分析了集肤效应与邻近效应对绕组的影响，建立了变压器谐波附加损耗模型。但该模型中涉及的变压器内部参数较多，公式较为复杂，且计算附加损耗时绕组支路的计算是在频域中进行的，而励磁支路是在时域中完成的，需要多次迭代计算。文献［12］对一种计及电压偏差和负载波动情况的配变损耗精确计算模型进行了分析，并用实例验证了所建模型可以提高线损计算的准确性，但该方法需要利用的各损耗系数的求取比较困难，损耗系数的计算与负荷曲线以及网络结构紧密相关，计算结果没有通用性。文献［13］提出了一种利用不平衡系数、负荷分布系数和单位电压损耗系数的电压损耗综合估算模型，但该模型没有解耦三相电流不平衡和电压偏差带来的附加损耗。文献［14］通过仿真验证了复合电能质量扰动下的低压配电网附加损耗并不等于各单一电能质量扰动单独存在时产生的附加损耗的简单叠加，然后提出了一种复合电能质量扰动的解耦方法，可以将附加损耗解耦成三相电流不平衡附加损耗与谐波附加损耗之和。

以上研究为本文研究的计及电能质量影响的10 kV配电网损耗计算模型提供了经验，但是实际的配电网可能同时包含多种电能质量扰动，而针对多种电能质量扰动下配电网损耗的系统量化评估还尚未开展。因此本文在分别分析单种电能质量扰动对配电网损耗影响的基础上，建立了同时考虑多种电能质量扰动影响的10 kV 配电网损耗评估方法与计算模型。

1 计及单种电能质量扰动影响的配电网损耗计算

由于实际的10 kV线路分支多，求解所有单一元件的损耗再相加显然是不现实的，本文重点研究计及单种电能质量扰动影响的10 kV 配电网损耗计算模型，其中产生损耗的主要元件是配变和线路。在配电网中，线路损耗都是可变损耗，而配变损耗包括配变固定损耗（铁损）和配变可变损耗（铜损）两部分。

1.1 计及谐波的10 kV配电网损耗计算

一般而言，电网谐波电压畸变率不大，其对变压器的固定损耗影响相对较小，可以忽略不计，因此通常只需要计及谐波电流对配电网可变损耗（线路的损耗和配变的负载损耗）的影响。由于间谐波和谐波本质上相同，谐波附加损耗分析同样适用于间谐波。

10 kV 系统中三相的谐波电流幅值和畸变率可能不同，此时需要分相计算各相谐波电流的损耗，当每台配变的谐波电流都得到监测时，可分段计算得到每段馈线的谐波附加损耗，最后累加得到总的谐波附加损耗，如式（1）所示。

式中：ΔPh为10 kV 配电网总谐波附加损耗；Rih、RTih分别为第i段线路和第i台配变的等值谐波电阻；L为该10 kV 馈线计算过程的线路分段数；M为该10 kV 馈线所包含的配变总台数；IRihA、IRihB、IRihC分别为第i段线路的A、B、C相的h次谐波电流的有效值；ITihA、ITihB、ITihC分别为第i台配变的A、B、C 相的h次谐波电流的有效值。

谐波电阻的阻值受集肤效应和邻近效应影响，与系统频率f有关。根据IEC60287标准，考虑磁滞、涡流和集肤效应后，导体的h次谐波交流电阻为：

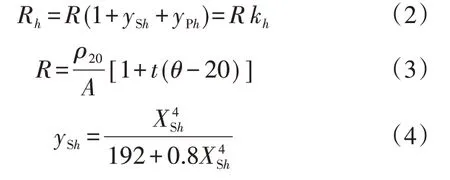
式中：Rh为导体的h次谐波交流电阻（Ω／m）；ySh、yPh分别为h次谐波作用下的集肤效应系数、临近效应系数，本文将kh=1+ySh+yPh定义为谐波系数；ρ20为导线材料在20 ℃下的电阻率（Ω·mm2／m）；A为导线的横截面积（mm2）；t为电阻温度系数；θ为导线的最高使用温度（℃）；fh为h次谐波频率；Dc为导线外径（mm）；s为导线中心轴之间的距离（mm）；ks、kp的取值如附录A表A1所示。

则单条线路的谐波可变损耗的附加损耗率（下文简称谐波可变附加损耗率）α如式（8）所示。

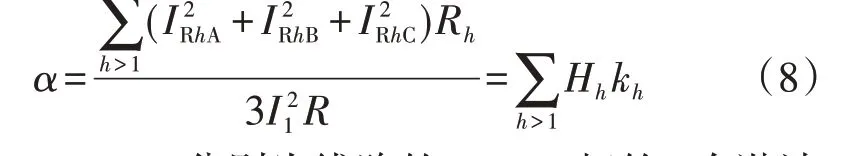
式中：IRhA、IRhB、IRhC分别为线路的A、B、C相的h次谐波电流；I1为线路基波电流；Hh为h次谐波电流含有率。

配变绕组在谐波作用下的负载损耗主要由三部分组成，即谐波电流对电阻损耗的影响（∝h），谐波电流对绕组涡流损耗的影响（∝h2），谐波电流对其他杂散损耗（∝h0.8）的影响。因此，在计及集肤效应和邻近效应对绕组电阻的影响后，h次谐波电流作用下的配变等值交流电阻RTh将增大为kThRT1（kTh∈［h，h2］，RT1为配变基波交流等值电阻），具体根据谐波损耗各个成分的占比来确定。则单台配变谐波可变附加损耗率α′如式（9）所示。kh和kTh的值仅与谐波次数有关，且一一对应，不随时间及电网运行状态变化，因此在工程应用中只需要测量配电网的各次谐波电流含有率Hh即可得到α和α′，从而计算出谐波附加损耗和总损耗。

1.2 计及三相电流不平衡的10 kV配电网损耗计算

配变固定损耗只受电压影响，在三相电流不平衡时几乎不变，因此对于配变本文只讨论三相电流不平衡影响下其可变损耗的变化。为了避免在计算电能质量扰动引起的附加损耗率时的重复计算问题，在分析三相电流不平衡带来的可变损耗的附加损耗率（下文简称三相电流不平衡可变附加损耗率）时，只考虑基波电流而不考虑谐波电流的影响。因此本文采用电流的基波负序分量I12与基波正序分量I11的比值来表示三相电流不平衡度β，即：

在不考虑电流畸变的情况下，采用对称分量法计算三相电流不平衡带来的损耗。

对于三相三线制线路，当三相负载电流不平衡时，线路损耗ΔPunb如式（11）所示。

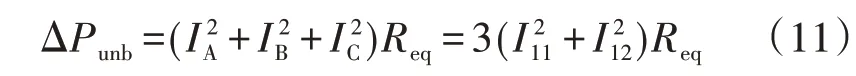
式中：IA、IB、IC分别为A、B、C 相负载电流；Req为端线（火线）等效电阻。

如果通过调整负载或投入治理装置，完全抑制三相电流不平衡负载电流中的负序电流，则电网只需传输三相平衡的正序电流，线路损耗达到最小值ΔPb，如式（12）所示。

根据上述分析易知，三相三线制线路的三相电流不平衡可变附加损耗率γ为：

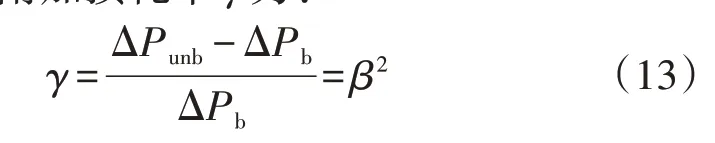
当三相四线制配电网三相电流不平衡时，不仅会和三相三线制线路一样在相线上引起损耗，中性线上还会流过零序电流I0从而产生额外的损耗，则此时三相四线制线路的损耗ΔP′unb为：

式中：β0为零序电流不平衡度。

10 kV 配变采用△／Y 联接，低压侧实际上相当于一段特殊的三相四线制线路，其中性点直接引出，等效于三相四线制线路的中性线上电阻为0。

因此在三相电流不平衡影响下，10 kV配变的可变损耗ΔP″unb为：

对于配电网中广泛存在的辐射状馈线，则首先需要进行馈线分段，计算出每段馈线的附加损耗后进行累加得到总的附加损耗，如式（18）所示。

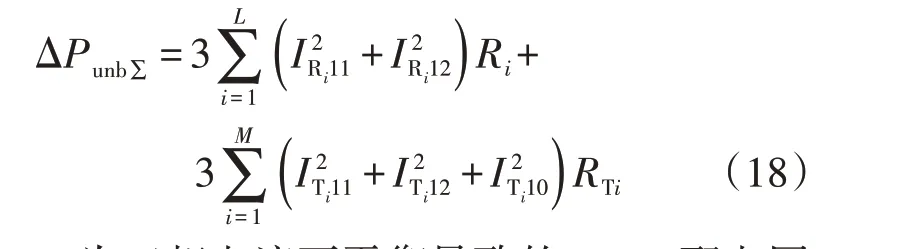
式中：ΔPunb∑为三相电流不平衡导致的10 kV配电网总损耗；Ri、RTi分别为第i段馈线和第i台配变的等值电阻；IRi11、IRi12分别为第i段馈线的基波正序电流和基波负序电流的有效值；ITi11、ITi12、ITi10分别为第i台配变的基波正序电流、基波负序电流和基波零序电流的有效值。

工程应用中，只需要测量三相基波电流的不平衡度β和零序电流不平衡度β0，即可得出三相电流不平衡可变附加损耗率，从而计算出三相电流不平衡引起的附加损耗（下文简称三相电流不平衡附加损耗）和总损耗。

1.3 计及电压偏差的10 kV配电网损耗计算

配变固定损耗指的是产生在配变等值并联电导上的损耗，其与负载电流无关，但是与电网运行电压的平方成正比［15］，即：

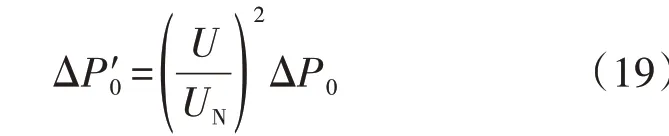
式中：ΔP′0为配变固定损耗；U为电网运行电压；UN为电网的额定电压；ΔP0为额定电压下配变的固定损耗。

则对于配变，电压偏差导致的固定损耗附加损耗率（下文简称电压偏差固定附加损耗率）λ0如式（20）所示。

式中：ΔU为电压偏差率，ΔU=(U-UN)/UN×100%。

当每台配变的电压都能够通过监测装置得到时，可以采用式（20）准确计算出各配变的电压偏差固定附加损耗率，然后通过加权累加就可以得到配变总的电压偏差固定附加损耗率λ0∑如式（21）所示。式中：λ0i为第i台配变的电压偏差固定附加损耗率；ΔP0i为第i台配变在额定电压下的固定损耗。

配变的可变损耗是指配变电阻上的损耗，其随负荷电流的变化而变化，与负荷电流的平方（或负载功率）成正比，如式（22）所示。

式中：P、Q分别为负载的有功功率、无功功率；φ为功率因数角，tanφ=Q/P；I为负荷电流。

为了定量分析电压偏差给配变可变损耗带来的影响，需要事先确定等值负荷静态电压特性在额定电压值处的斜率，即通过经验或者测量获得等值负荷的有功功率静态电压特性系数χ和无功功率静态电压特性系数δ，其中［16］：

根据泰勒级数展开，保留ΔU的平方项，忽略更高阶的微小分量，可得当系统电压发生偏差后，负载的有功功率P′和无功功率Q′为：

系统电压发生偏差后的有功功率P′、无功功率Q′及功率因数角φ′都是可以直接测量的，而系统电压发生偏差前的有功功率P和无功功率Q可以根据有功功率静态电压特性系数和无功功率静态电压特性系数由式（24）反推出来，然后将其代入式（25）即可得系统电压无偏差时的配变可变损耗如式（27）所示。

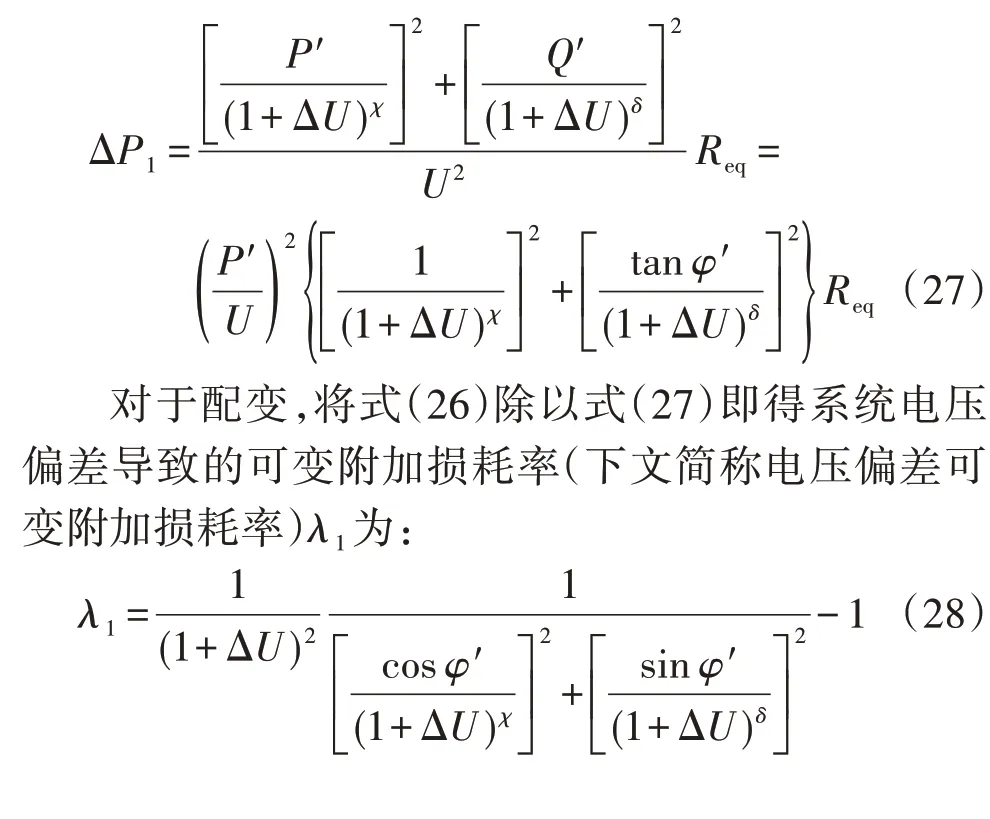
下面给出一些典型负荷的计算结果分析：

1）若不考虑负荷的电压调节效应，即将负荷看作恒功率负荷，则χ=0、δ=0，此时λ1≈-2ΔU-(ΔU)2，即适当升高电网运行电压有利于降低配变可变损耗。

2）若将负荷看作恒电流，则有χ=1、δ=1，此时λ1=0，即配变可变损耗不受电压偏差影响；

3）若将负荷看作恒阻抗，则χ=2、δ=2，此时λ1=2ΔU+(ΔU)2，即适当降低电网运行电压有利于降低配变可变损耗。

电压偏差影响下线路可变损耗的分析与计算方法与配变相同，在此不再赘述。

在工程应用中，通过测量负荷的有功功率静态电压特性系数χ、无功功率静态电压特性系数δ、功率因数角φ′以及电压偏差率ΔU可以得到配变和线路的电压偏差可变附加损耗率λ1、λ2，从而计算出电压偏差引起的附加损耗和总损耗。

2 考虑电能质量影响的配电网损耗综合评估模型

2.1 10 kV配电网综合损耗评估方法

当电网同时存在多种电能质量扰动时，理论上可以借助式（8）、（9）、（13）、（15）、（17）、（21）和式（28）分别评估各电能质量扰动引起的附加损耗率，进行综合后即可得到所有电能质量扰动引起的配电网总附加损耗。计算的关键在于要分析解耦各电能质量扰动引起的附加损耗可能存在的相互影响，避免漏算和重复计算。考虑到配电网的损耗分为固定损耗和可变损耗，两者受电能质量扰动影响的规律和程度都不一样，因此首先应该将配电网的固定损耗和可变损耗进行分离。其中，固定损耗主要受电压偏差影响，其他电能质量扰动对其影响很小，可忽略不计；在评估可变损耗时，谐波、三相电流不平衡、电压偏差3 个因素存在一定的耦合关系，需要进行解耦。综上所述，考虑电能质量扰动的10 kV配电网综合损耗评估方法如图1所示，具体步骤见2.2节。

图1 考虑电能质量扰动的10 kV配电网综合损耗计算方法Fig.1 Calculating method of comprehensive loss of 10 kV distribution network considering power quality disturbances

2.2 10 kV配电网综合损耗计算步骤

1）分离出配电网的固定损耗，估算出电压偏差影响下固定损耗的附加损耗率。固定损耗是产生在电力线路和配变等值并联电导上的损耗，与电压有关，配电网的固定损耗主要是配变的固定损耗。当每台配变的电压都可通过监测装置得到时，采用式（21）计算电压偏差导致的配网固定损耗的附加损耗率λ0Σ，从而精确计算出发生电压偏差后配电网的固定损耗ΔP′0为：

2）分别估算谐波、三相电流不平衡、电压偏差影响下线路和配变可变损耗的附加损耗率。可变损耗指的是消耗在电力线路和配变电阻上的损耗，与负荷电流有关。当配电网各元件的谐波畸变率都存在监测值时，可以由式（8）和式（9）较为精确地估算谐波可变附加损耗率。按照式（13）、（15）和式（17）计算三相电流不平衡可变附加损耗率，按照式（28）计算电压偏差可变附加损耗率。

3）综合上述受单种电能质量扰动影响的可变损耗附加损耗率，分别得到线路和配变损耗受电能质量影响的可变损耗综合附加损耗率。

单种电能质量扰动导致的可变附加损耗可以直接相加，但是其附加损耗率如果要直接相加，则需要其基准值相同。在计算谐波、三相电流不平衡和电压偏差导致的可变附加损耗率时，都应该以元件在基波正序电流单独作用下的可变损耗作为基准。其中，谐波和三相电流平衡度变化时基波正序电流是不变的，其作用下的可变损耗也不变，可以直接测得。但是，电压偏差影响下的基波正序电流会产生变化，而电压偏差附加可变损耗率的基准定义为无电压偏差时元件在基波正序电流作用下的可变损耗，无法在存在电压偏差时直接测得。所以电压偏差可变附加损耗率在综合计算模型中，不能与其他电能质量扰动引起的可变附加损耗率直接相加。然而2 个基准值比值恰好就是解耦后的电压偏差可变附加损耗率，因此可以采用相乘的方式计算综合附加损耗率。

通过上述分析可知，电能质量扰动造成单一元件可变损耗的综合附加损耗率μ为：

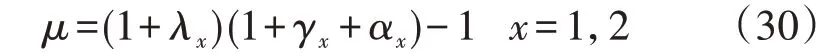
式中：x取值为1、2分别表示配变、线路，将对应元件的参数代入公式即可。

4）综合固定损耗和可变损耗的附加损耗率，得到计及电能质量扰动影响时配电网的总损耗。实际配电网中广泛存在辐射状馈线，所以需要分段计算线路和配变的损耗，最后相加得到配电网的总损耗，如式（31）所示。

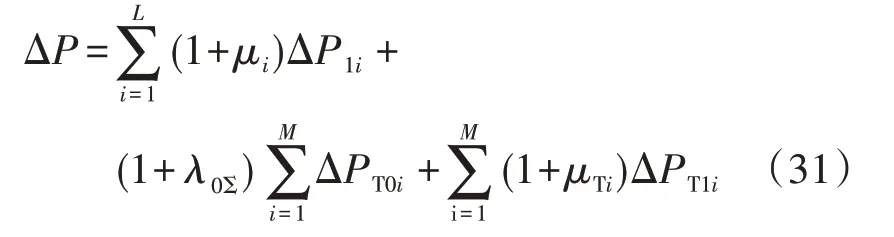
式中：ΔP为10 kV 配电网总损耗；ΔP1i和ΔPT1i分别为第i段馈线和第i台配变在基波正序电流作用下的可变损耗；ΔPT0i为第i台配变在额定电压下的固定损耗；μi和μTi分别为第i段馈线和第i台配变的综合附加损耗率，由式（30）计算得到。

因此，整个配电网的总附加损耗率为：

3 物理实验及结果分析

3.1 实验方案及参数

为验证本文的计算方法，基于国家电网公司电力谐波特性分析评估技术实验室的10 kV／2 MV·A电能质量扰动测试平台，搭建了含10 kV／0.4 kV 的配变、380 V 配电线路和负载等的实验环境进行实验。电能质量综合试验平台主电路拓扑图如附录A图A1 所示。其中，10 kV 电能质量扰动模块由链式多电平逆变器构成，可模拟10 kV 电压等级的谐波电压、三相不平衡电压和电压波动；380 V 电流扰动源由电容柜、电抗柜及基于电力电子装置的电流扰动发生器组成，可以模拟380 V 电压等级的无功负载、三相不平衡负载和非线性负载；待测试的10 kV 配变和380 V 配电线路串联在10 kV 电能质量扰动模块和380 V 电流扰动源之间。实验中使用的配变型号为S11-M-315／10，380 V 配电线路为架空线路，型号为JKLYJ-1kV1×185，线路长度为160 m。具体参数如附录A 表A2 和表A3 所示。负载为多级可调负载箱，每级可调功率60 kW，最大功率360 kW，实验中调至120 kW。实验中的采样频率为50 kHz，在配变高、低压侧和线路首、末端分别设置测量点，采用录波仪同时采样每个测量点的每相电压值和电流值，以保证采样精度。实验现场图如附录A图A2所示。

实验过程中，设置2 种工作方式：①恒负载，即380 V 低压侧投入固定的电抗负载，由10 kV 电能质量扰动模块产生带有电能质量扰动的电压，从而在实验设备上产生各种电能质量扰动；②380 V电流扰动源和10 kV 电压扰动源同时投入，10 kV 电能质量扰动源产生带有电能质量扰动的电压，且低压侧负载设置为具有电能质量扰动的恒流源。

3.2 谐波实验

调节10 kV 电能质量扰动模块在基波中分别叠加2—25 次谐波电流，各次谐波的含有率以5%为步长在5%～20%之间变化。各实验工况稳定运行后保持该工况下电压、电流不变，此时可认为谐波功率保持不变，然后利用MATLAB 对稳定时的10 个周期的电压和电流数据进行分析得到实测值。

对于线路，首先对测得的线路电流和线路首、末端电压值进行滑动窗快速傅里叶变换（FFT），分离出基波和各次谐波的值，然后利用P=UIcosφ得到线路首、末端的三相基波功率和谐波功率实测值，取首、末端的差值作为损耗ΔP实测值，谐波附加损耗率即为谐波附加损耗与基波损耗的比值，再利用ΔP=I2R得到基波电阻和各次谐波电阻的实测值，将基波电阻近似认为是直流电阻，谐波电阻和基波电阻的比值即为谐波系数实测值。将以h倍直流电阻等效h次谐波电阻的常用模型［5-6］（下文简称常用模型）作为对比模型，常用模型中kh=h；本文模型中，采用式（3）—（7）计算线路的谐波系数kh=1+ySh+yPh，采用式（8）计算线路的谐波可变附加损耗率。

线路的谐波可变附加损耗率的实验实测值、本文模型计算值和常用模型［5-6］计算值的对比如图2所示，谐波系数的实测值和计算值对比如附录A 图A3所示，同次谐波下不同谐波含量的线路的谐波可变附加损耗率实测值和计算值对比图如附录A 图A4所示。

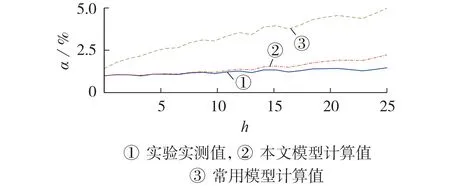
图2 谐波含量为10%时线路谐波可变附加损耗率的实测值和模型计算值对比Fig.2 Comparison between measured value and model calculated value of line harmonic variable additional loss rate when harmonic content is 10%

由图A3 和图2 可见，随着谐波次数的增大，线路的谐波系数和谐波可变附加损耗率增加，本文模型的计算结果的误差也随之增大，但是与常用模型相比，本文模型的误差较小，因此本文模型更加精确。由图A4可见，对同次谐波而言，谐波含量越高，线路的谐波可变附加损耗率越大，本文模型的计算误差越小。在考虑实验测量误差和计算误差等因素后，低次谐波的误差在可接受范围内，可验证1.1 节中的线路谐波损耗计算模型在低次谐波下的正确性。由于实际配电网中低次谐波含量较高，该模型可应用于实际配电网线路的谐波损耗计算中。

配变谐波实验的数据处理方法与线路的相同，首先分离出测量得到的配变高、低压侧电流和电流基波及各次谐波的值，然后利用P=UIcosφ得到配变高、低压侧的三相基波功率和谐波功率实测值，取高、低压侧的功率差值作为损耗值，此时得到的是总谐波附加损耗。同时，为了分离出带载时变压器的谐波可变附加损耗实测值，需要进行相同谐波条件下的变压器空载实验，利用P=UIcosφ计算得到谐波附加固定损耗实测值。则带载时的谐波附加可变损耗实测值为总谐波附加损耗实测值与对应空载实验测量所得的谐波附加固定损耗的差值，谐波附加可变损耗率为谐波附加可变损耗与基波损耗的比值。

本文模型采用式（9）计算配变谐波可变附加损耗率，根据谐波损耗成分占比取kh=h。配变谐波附加可变损耗率的实验实测值、本文模型计算值以及文献［9］中采用谐波损耗因子的模型的计算值的对比如图3所示。由图3可看出，配变谐波可变附加损耗率随着谐波次数的增大而增加；低次谐波下，采用本文模型计算得到的谐波可变附加损耗率的误差较小，高次谐波下则误差较大，但均小于文献［9］中模型对应的误差，这说明1.1节中的配变谐波损耗计算模型优于常用模型。考虑实际配电网中的谐波情况，本文配变谐波损耗计算模型可应用于实际配电网的配变谐波损耗计算中。

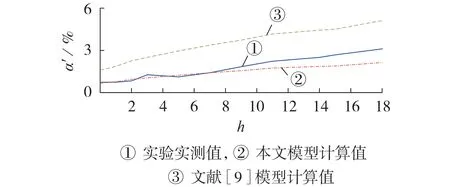
图3 谐波含量为10%时配变谐波可变附加损耗率的实测值和模型计算值对比Fig.3 Comparison between measured value and model calculated value of distribution transformer harmonic variable additional loss rate when harmonic content is 10%

3.3 三相电流不平衡实验

调节10 kV 电能质量扰动源使三相电流不平衡度在0～20%之间以2%为步长变化。利用MATLAB分析稳定时测量点采样所得的10 个周期的数据。为了解耦各类电能质量扰动问题引起的附加损耗，三相电流不平衡实验中只考虑基波损耗。首先对测得的电流和电压数据进行滑动窗FFT 分析，从而分离出基波值，然后使用对称分量法分离出基波的正序、零序和负序值，再利用P=UIcosφ计算三相电流不平衡时的损耗实测值。三相电流平衡时的损耗实测值则取基波正序电流和电压作用下的基波正序损耗值，三相电流不平衡附加损耗实测值为三相电流不平衡损耗实测值与三相电流平衡时的损耗实测值的差值。三相电流不平衡附加损耗率实测值即为三相电流不平衡附加损耗值与三相电流平衡时的损耗值的比值。

对于线路，测量的电量为线路电流和首末端电压，线路损耗实测值取线路首、末端三相功率的差值。然后依次计算三相电流不平衡附加损耗实测值和三相电流不平衡附加损耗率实测值。配电网中的380 V 线路为三相四线制，因此三相电流不平衡时，本文模型采用式（14）计算线路损耗，采用式（15）计算三相电流不平衡附加损耗率。线路三相电流不平衡附加损耗率的实验实测值与本文模型的计算值以及文献［10］中采用三相电流幅值不平衡度作为指标的模型的计算值的对比如图4所示。

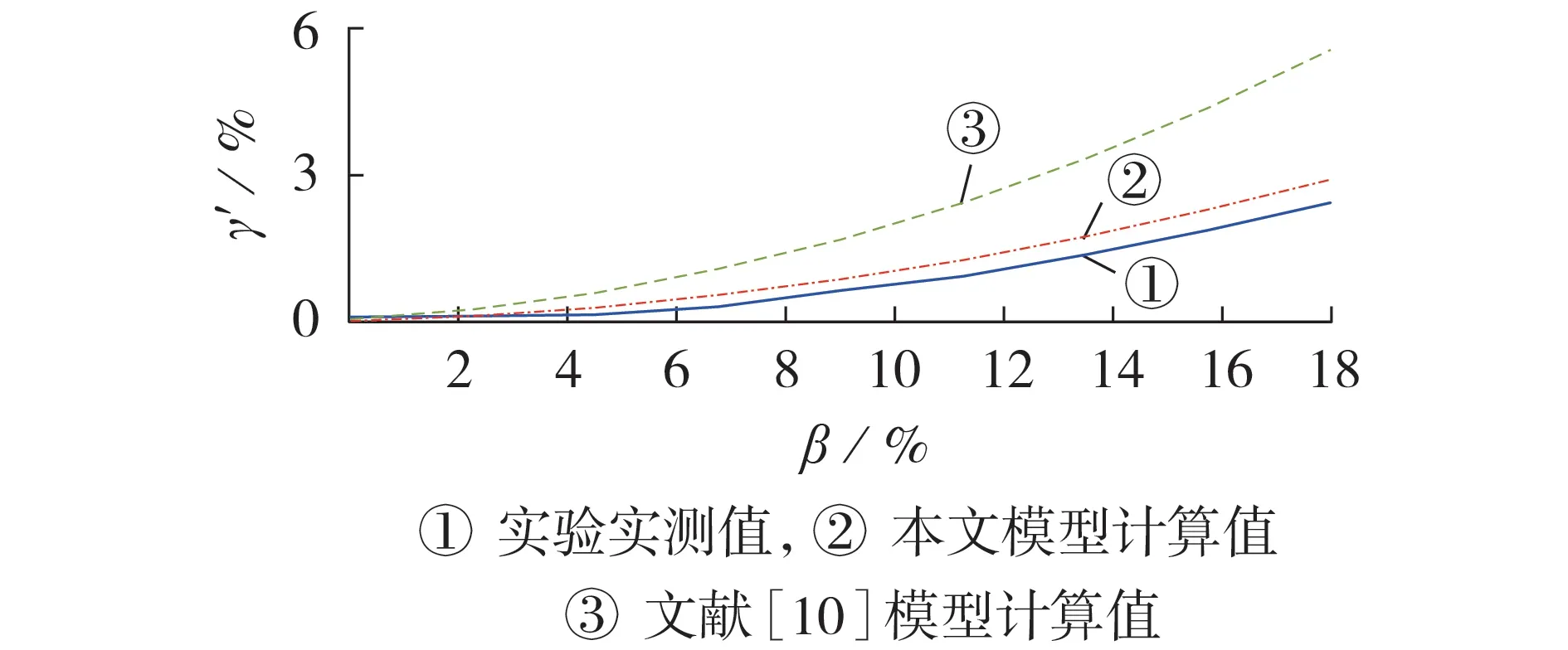
图4 线路三相电流不平衡可变附加损耗率的实测值和模型计算值对比Fig.4 Comparison between measured value and model calculated value of three-phase current unbalanced line variable additional loss rate

由图4 可看出，随着三相不平衡度的增加，线路的三相不平衡可变附加损耗率增大；本文模型的计算误差较小，且小于文献［10］中模型的计算误差。考虑测量误差和计算误差等因素，本文模型的计算误差在可接受范围内，可验证1.2节中线路三相不平衡损耗计算模型的有效性和精确性。

对于配变，测量的电量为配变高、低压侧的电压和电流值，配变损耗实测值取高、低压侧三相功率的差值。本文模型采用式（16）、（17）分别计算配变的三相电流不平衡可变损耗、三相电流不平衡可变附加损耗率。配变的三相不平衡可变附加损耗率的实验实测值与本文模型的计算值以及文献［11］中模型的计算值的对比如图5所示。

由图5 可看出，随着三相不平衡度的增加，配变的三相电流不平衡可变附加损耗率增大，本文模型的误差也随之增大，但比文献［11］中的模型的误差小，表明1.2节中的配变三相不平衡损耗计算模型更为精确。

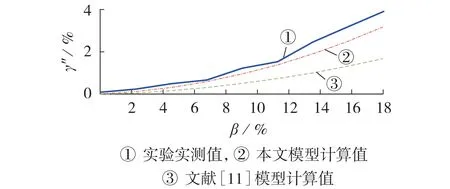
图5 配变三相电流不平衡可变附加损耗率的实测值和模型计算值对比Fig.5 Comparison between measured value and model calculated value of three-phase current unbalanced distribution transformer variable additional loss rate

3.4 电压偏差实验

调整10 kV 电能质量扰动源的相电压与额定电压的偏差在-10%～10%之间以2%为步长变化。由于所带负载为恒阻抗负载，取χ=2、δ=2，电压偏差影响下的固定损耗和可变损耗附加率计算公式相同，因此依然分别分析线路和配变的损耗。

为了解耦各类电能质量扰动引起的附加损耗，电压偏差实验中同样只考虑基波损耗，与三相电流不平衡实验的数据处理方法类似，首先分离出基波值，利用P=UIcosφ计算电压偏差损耗值，并将电压偏差为0 时的损耗实测值作为参考值，则两者的差值为电压偏差附加损耗实测值。电压偏差附加损耗率实测值为电压偏差附加损耗实测值与无电压偏差时的参考值的比值。

线路损耗实测值取线路首、末端三相基波功率的差值，再依次计算电压偏差可变附加损耗实测值和电压偏差可变附加损耗率实测值。本文模型基于1.3 节计算电压偏差可变附加损耗率。线路电压偏差可变附加损耗率λ2的实测值和本文模型的计算值以及文献［13］取不平衡系数为1 的模型的计算值的对比如图6所示。

图6 线路电压偏差可变附加损耗率的实测值和模型计算值对比Fig.6 Comparison between measured value and model calculated value of line voltage deviation variable additional loss rate

由图6 可看出，随着电压偏差的增大，线路的电压偏差可变附加损耗率增大；本文模型的计算误差很小，且小于文献［13］中模型的计算误差，这表明1.3 节中计及电压偏差的损耗计算模型优于常用模型，精确度较高。

配变的损耗实测值取为高、低压侧三相基波功率的差值，本文模型采用式（28）计算配变电压偏差可变附加损耗率，则配变电压偏差可变附加损耗率的实测值和本文模型计算值以及文献［12］中模型的计算值的对比如图7所示。

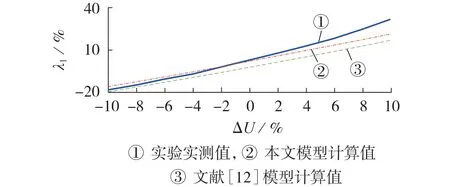
图7 配变电压偏差可变附加损耗率的实测值和模型计算值的对比Fig.7 Comparison between measured value and model calculated value of distribution transformer voltage deviation variable additional loss rate

由图7 可看出，随着电压偏差的增大，配变的电压偏差可变附加损耗率增加，考虑实验测量误差和计算误差等因素，本文模型的计算误差在可接受范围内，且比文献［12］中模型的计算结果误差小，这验证了1.3节的计及电压偏差的损耗计算模型的有效性。

3.5 复合电能质量扰动实验

首先在额定状态下运行实验平台，测量得到无电能质量扰动影响的电压和电流值，利用P=UIcosφ计算得到配电网的全波损耗实测值作为参考值；然后调节10 kV 电能质量扰动源在基波中叠加组合次谐波电流，同时调整三相电流不平衡度和电压偏差，使配电网中存在多种电能质量扰动。分析测量数据，得到复合电能质量扰动影响下的配电网全波损耗实测值，其与参考值之间的差值即为复合电能质量扰动带来的附加损耗实测值，总附加损耗率实测值则为附加损耗值与参考值的比值，本文模型采用式（32）计算总附加损耗率。表1 为多组实验中的配电网总附加损耗率实测值和本文模型的计算值的对比。

表1 复合电能质量扰动影响下附加损耗率实测值和模型计算值Table 1 Measured value and calculated value of additional loss rate under influence of compound power quality disturbances

由表1 可看出，在谐波、三相电流不平衡和电压偏差的复合电能质量扰动的影响下，本文模型的计算误差更小，可验证本文提出的复合电能质量扰动影响下的配电网综合损耗计算模型在实际应用中的有效性。

4 结论

1）本文分别提出了谐波、三相电流不平衡、电压偏差3 类电能质量单独作用下的配电网损耗和附加损耗率的计算模型，并通过物理实验验证了模型的有效性。同时对比了常用的计及单一电能质量扰动的损耗计算模型，结果表明本文模型能够更加精确地计算配电网损耗。

2）本文提出了考虑谐波、三相电流不平衡和电压偏差的复合电能质量扰动的10 kV 配电网损耗计算模型。该模型将配电网损耗分为固定损耗和可变损耗，对各类电能质量扰动的影响进行解耦，利用单一电能质量扰动导致的附加损耗率计算出配电网的总附加损耗率，从而计算配电网总损耗。通过物理实验验证了本文配电网损耗综合评估模型在复合电能质量扰动影响下的有效性，该模型应用于实际10 kV 配电网损耗的计算中时可以有效提高计算的准确度。

附录见本刊网络版（http：//www.epae.cn）。