基于柔性策略-评价网络的微电网源储协同优化调度策略

刘林鹏，朱建全，陈嘉俊，叶汉芳

（华南理工大学电力学院，广东 广州 510640）

0 引言

近年来，为了实现可再生能源的就地消纳，微电网中可再生能源的占比日益提高［1-2］。为抑制可再生能源的间歇性和随机性，维持微电网的稳定运行，有必要装设一定比例的储能，实现源储协同运行［3］。在这种背景下，如何充分地考虑可再生能源与储能系统的特点，对微电网进行源储协同优化调度成为一个热点问题。

目前，微电网的优化调度问题已经得到了大量的研究。已有的方法可以分为基于模型的数学优化算法和无模型的强化学习算法2 类。基于模型的数学优化算法通常是通过直接求解集中式的数学优化问题以获取最优策略。例如：文献［4］将微电网调度问题转化成二次型最优控制问题，并利用黎卡提方程解的特性对其进行求解；文献［5］将微电网调度问题转化为二阶鲁棒优化模型，利用列约束生成和强对偶原理将原问题分解后交替求解；文献［6］使用KKT（Karush-Kuhn-Tucker）条件及二阶锥松弛技术将微电网调度模型转换为单层的混合整数线性规划问题，并调用CPLEX 求解器对其进行求解；文献［7］构建了微电网双层调度模型，并利用交替方向乘子法对其进行求解。上述文献为求解微电网优化调度问题，对原问题中的非凸非线性约束进行了一定简化处理。这些简化处理方法通常建立在一定假设的基础上，它们求得的最优策略与原问题的最优策略在某些情况下并不等价。无模型的强化学习算法将智能体不断与环境进行交互，通过观察交互后得到的结果改进策略。例如：文献［8］使用基于值的深度Q 网络DQN（Deep Q-Network）算法得到了微电网的在线调度策略；文献［9］使用基于随机性策略的策略-评价网络AC（Actor-Critic）算法求解微电网的最优调度策略；文献［10］使用基于确定性策略的深度确定性策略梯度DDPG（Deep Deterministic Policy Gradient）算法求解微电网中共享储能的最优控制问题。上述强化学习算法相较于基于模型的数学优化算法的优势在于其不需要模型的信息，可通过观察到的数据寻找最优策略。此外，其得到的策略泛化能力强，在强随机性环境下有较好的表现［8-9］。尽管强化学习方法在微电网优化调度问题的求解过程中有较好的表现，但由于它在训练过程中为保证智能体的探索性能，往往需要在策略探寻过程中加入一定的随机性，这可能导致所搜寻的策略不满足约束条件。为解决这个问题，已有的文献主要采取了以下措施：文献［11］结合了壁垒函数的特性以保证智能体在满足约束的条件下进行策略学习；文献［12］通过在奖励函数中设置惩罚因子，使智能体在学习过程中避开不满足约束条件的策略；文献［13］使用元学习的方式使得策略更新过程满足约束条件。上述方法本质上都是通过无模型学习的方式使得智能体朝着满足约束条件的方向对策略进行更新，但这类方法并不能保证所得策略严格满足约束条件。

针对以上问题，本文结合有模型的数学优化与无模型的强化学习的思想，提出了一种基于柔性策略-评价网络SAC（Soft Actor-Critic）的微电网源储协同优化调度方法。一方面，所提方法在不对原问题进行简化处理的前提下，利用强化学习算法将原问题分解为多个子问题进行求解，并通过贝尔曼最优定理保证了所得策略与原问题最优策略的等价性；另一方面，所提方法利用部分模型信息使得策略严格满足约束条件。此外，为减少智能体在训练过程中与环境的交互时长，本文提出了一种基于深层长短期记忆LSTM（Long Short-Term Memory）网络的环境建模方法。

1 微电网源储协同调度模型

1.1 目标函数

以微电网的运行成本最小化为目标，则有：

式中：Pg，t和Ps，t分别为t时段机组g和储能s的有功出力，Ps，t取值为正时表示储能放电，取值为负时表示储能充电，其最大值为Pmaxs；Pl，t为t时段联络线l传输的有功功率，其取值为正时表示从主网购电，取值为负时表示向主网售电；og，t为t时段机组g状态，其取值为0时表示处于离线状态，取值为1时表示处于工作状态；ct为t时段即时成本。

1.2 马尔可夫决策过程

在利用强化学习求解优化问题时，需要先将原问题构建为一个马尔可夫决策过程［14］。本文从时间维度对原问题进行解耦，构建了以下的马尔可夫决策过程。

1）状态。

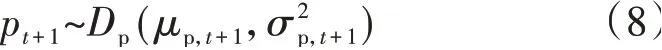
式中：Pcha，t和Pdis，t分别为t时段储能的充电和放电功率；η为储能的充放电效率系数；μL，t+1、μwt，t+1、μpv，t+1和μp，t+1分别为分布DL、Dwt、Dpv和Dp的均值；σL，t+1、σwt，t+1、σpv，t+1和σp，t+1分别为分布DL、Dwt、Dpv和Dp的标准差。

4）奖励。

奖励是智能体每次与环境进行交互时收到的反馈信号，可用于指导策略的更新方向。为了实现微电网的运行成本最小化，本文将奖励设置为即时成本的负值：

式中：rt为t时段智能体在状态st下做出动作at获得的奖励。

5）环境。

在本文的微电网源储协同优化调度模型问题中，智能体所处的环境为原问题在时间维度解耦后的单时段优化问题：

在微电网源储协同调度问题中，决策变量包含机组出力、储能充放电功率、机组的启停状态以及联络线功率。若直接用无模型的强化学习算法搜寻这4 个变量对应的策略，将无法保证其搜寻的策略严格满足约束条件。为解决这一问题，将这4个变量分成了两部分：一部分为储能充放电功率和机组的启停状态，这部分变量通过强化学习的策略网络输出得到；另一部分为机组的出力和联络线功率，这部分变量由策略网络输出储能充放电功率和机组的启停状态后通过CPLEX 商业求解器求解式（10）—（15）组成的单时段的优化问题得到。通过这种方式求解这4个决策变量可以保证它们严格满足约束条件。

2 基于SAC的源储协同优化调度

2.1 SAC优化策略

2.1.1 智能体的目标函数

SAC 算法作为无模型的强化学习算法之一，能够有效地在模型未知的情况下，通过不断地与环境进行交互以搜寻最优策略［15］。本文将利用SAC算法学习最优策略的智能体称为SAC智能体。在微电网源储协同优化调度问题中，SAC 智能体的目标可定义为最大化智能体调度周期内的总奖励与策略熵的期望值［16］：

通过求解式（18）所示的目标函数，所得策略便可实现总奖励的最大化（即运行成本最小化）。另一方面，由于目标函数考虑了将策略熵最大化，所得策略具有更强的探索性能以及更好的鲁棒性。

2.1.2 智能体结构

式中：γ为奖励折扣系数。

根据贝尔曼方程，可以推导出状态-动作值函数Qπ(st，at)的递归方程为［14］：

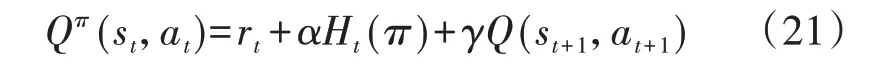
2.1.3 评价网络的参数更新

对于评价网络，其参数是朝着真实状态-动作值函数的方向更新的。因此，基于式（21）以及时序差分算法可得SAC 智能体评价网络的参数更新公式为［17］：

式中：θQ和θπ分别为评价网络和策略网络的参数，可利用文献［18］所提的小批量梯度下降法分别求解式（22）和式（24）以获得θQ和α的更新值；H′为目标策略熵；M为小批量更新的样本数量；i表示样本编号，每个样本由(si，ai，ri，s′i)构成，其中s′i为转移后状态；a′i为智能体在s′i下根据当前策略所得动作。智能体每次与环境进行交互时均会产生一个样本，并将其存入经验回放池中［19］。

2.1.4 策略网络的参数更新

对于策略网络，其参数是朝着最大化总奖励和策略熵的方向进行更新的。因此，可利用梯度上升法求解式（25）对其参数θπ进行更新。

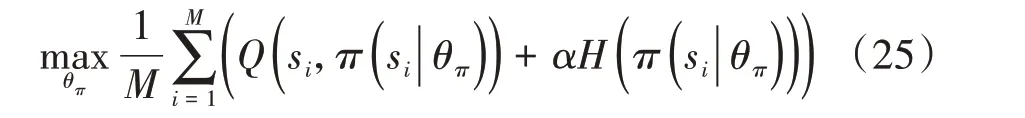
SAC 智能体不断地与环境进行交互产生新的样本并存入经验回放池中，且每次与环境进行交互后都根据经验回放池中的样本对评价网络和策略网络进行一次参数更新。在超参数设置合理的前提下，通过一定次数的交互训练后，SAC 智能体的策略最终可收敛到最优策略［20］。

通过这种方式，可以将原问题分解为多个子问题求解。根据贝尔曼最优定理，所得策略与原问题最优策略具有等价性，相关证明见附录B。

2.2 基于深层LSTM网络的环境建模

由于SAC 智能体每次与环境进行交互时，都需要求解一个由式（10）—（16）组成的单时段优化问题，这将导致训练的时间大幅增加。为加快SAC 智能体的训练速度，本文利用深层LSTM 网络对环境进行建模。

深层LSTM 神经网络是循环神经网络RNN（Recurrent Neural Network）的一种类型，其基本结构如附录C 图C1所示。从图中可以看出，RNN 的隐藏层包含了当前时刻的输入信息以及上一时刻的输入信息，因此它具有记忆功能。为解决RNN 的梯度爆炸和消失问题，LSTM 对RNN 进行了改进，其结果如附录C 图C2 所示，图中σ表示Logistic 函数，输出区间为（0，1）。LSTM 在RNN 的基础上引入内部状态ct，用于传递循环信息，引入外部状态ht用于接收内部状态传递的信息，具体如下：

式中：⊙表示向量元素相乘；ft、it、ot分别为遗忘门、输入门和输出门，它们控制其对应的信息通过比例，且ft、it、ot中各元素取值范围为［0，1］；Wc、Uc和bc为可学习的神经网络参数。

与传统的前馈神经网络类似，使用小批量梯度下降法更新LSTM网络参数θn：

式中：K为小批量样本数目；xj、yj分别为样本j的特征与标签；ŷj为样本j的LSTM 网络输出量；β为学习率。

3 算例分析

3.1 参数设置

以图1 所示的微电网为例对所提方法进行测试，相关参数见附录D。评价网络与策略网络结构参数以及用于环境建模的深层LSTM 网络超参数见附录E。所有算例均基于MATLAB R2021a实现，并在64位Windows系统、Intel Core i7-6700K@3.7 GHz的环境下运行。

图1 微电网结构Fig.1 Structure of microgrid

由于深层LSTM 网络的训练是一种“端到端”的有监督学习方法，因此在训练前，首先需要准备一定数量的样本。本文通过CPLEX 商业求解器求解1 000 个不同场景下由式（10）—（16）组成的优化问题，得到了1 000 个样本，并将90%的样本作为训练集，用于训练深层LSTM 网络；将其余10%的样本作为测试集，用于测试模型的准确性。每个样本包含了用于训练的标签和特征，其中标签为ct，特征为{Ps，t，og，t+1，ES，t，pt，Pwt，t，Ppv，t，Lt，og，t}。

3.2 智能体的离线训练过程

为验证SAC 智能体在随机环境下的学习能力，假设负荷、风电出力、光伏出力和电价分别服从式（31）—（34）中均值和标准差的高斯分布。

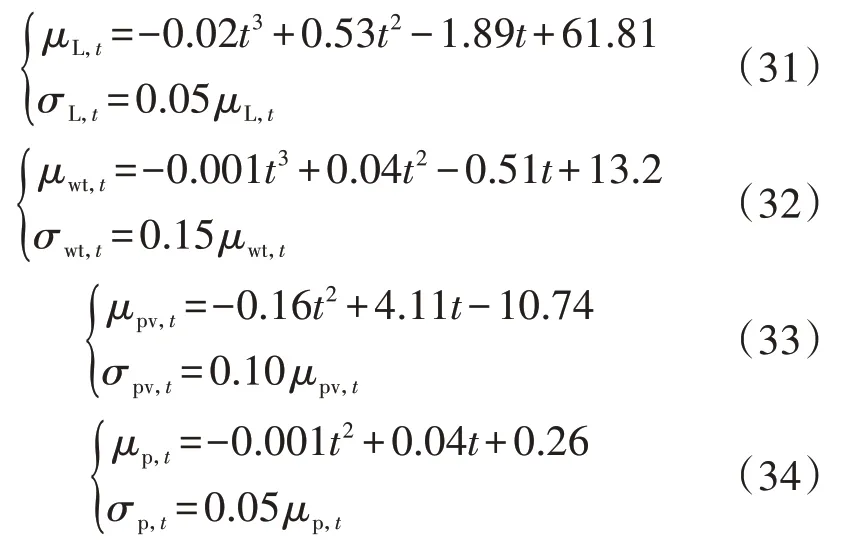
图2 展示了SAC 智能体在设置的随机环境训练时，微电网的运行成本期望随训练次数增加而变化的过程，其中该期望值通过最近100 次训练结果的平均值近似表示。从图2 中可以看出：在训练前期，微电网运行成本的期望值随着训练次数的增加而降低；在完成2 400 次训练之后，微电网运行成本的期望值基本保持不变，因此可以认为此时SAC 智能体找到了近似最优策略。

图2 SAC智能体训练过程Fig.2 Training process of SAC agent

为验证本文所提方法的优势，图3 展示了无模型的SAC智能体在设置的随机环境训练时的运行成本变化情况。其中，无模型的SAC 智能体采用了文献［12］中的方法，在奖励函数中对于不满足约束条件的策略设置了惩罚因子。在本算例中，对不满足式（12）的策略增加一个值为$200 的惩罚成本。从图3 中可以看出，这种在奖励函数中增加惩罚因子的无模型强化学习方法无法保证策略严格满足约束条件，造成其运行成本产生较大波动。

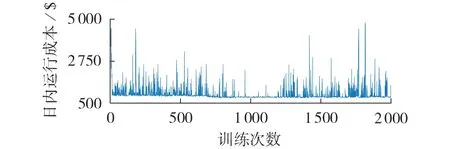
图3 无模型的SAC智能体训练过程Fig.3 Training process of model-free SAC agent

3.3 智能体在线决策分析

将离线训练后的SAC智能体用于微电网源储协同优化调度的在线决策，并与短视（myopic）策略进行对比。其中，短视策略通过求解式（35）中的单时段优化问题得到。

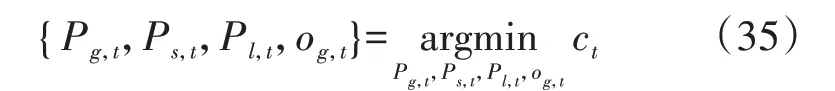
图4 展示了2 种策略连续进行1 个月的在线决策的情况。从图中可以看出，所提方法的优化效果明显优于短视策略。采用短视策略时，微电网在该月运行成本均值为$766.90；而采用本文策略后，微电网在该月运行成本均值为$726.36（比短视策略所得运行成本降低了5.29%），这主要得益于本文所提的方法具有远视能力，能全局考虑调度周期内的情况以获得更优的结果。

图4 运行1个月的结果对比Fig.4 Comparison of results in a month

进一步地，图5 以第一天的在线决策结果为例，详细展示了采用本文所提方法进行在线决策时各时段的状态变量以及动作变量情况。可以发现，在电价较低时，微电网需要从主网购电以满足负荷需求。由于此时微电网自备机组的运行成本比购电成本高，所以发电机处于停机状态。另一方面，储能选择在电价较低时尽可能充电，随后在电价较高时放电以获取更高的利益。

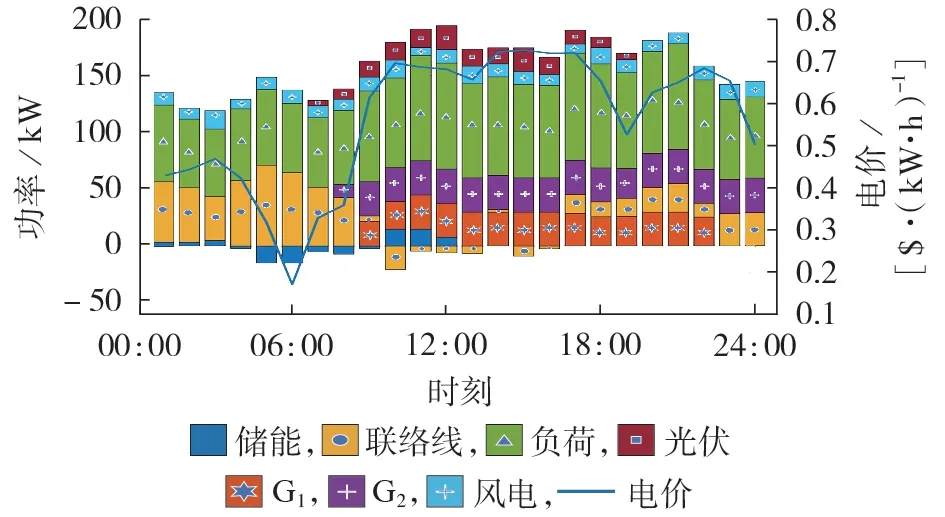
图5 日内在线决策结果Fig.5 Intra-day online decision results

3.4 LSTM网络环境建模分析

为测试本文所提的LSTM 网络环境建模方法的有效性，将基于原环境和深层LSTM 网络模型得到的微电网的源储协同优化调度策略进行对比分析。

图6 展示了不同测试场景下基于原环境和深层LSTM 网络模型得到的成本对比情况。从图中可以看出，基于深层LSTM 模型的输出成本曲线与基于原环境的成本曲线基本重合，均方根误差仅为0.315 3，这说明深层LSTM 模型所建的环境与原环境近似等效。

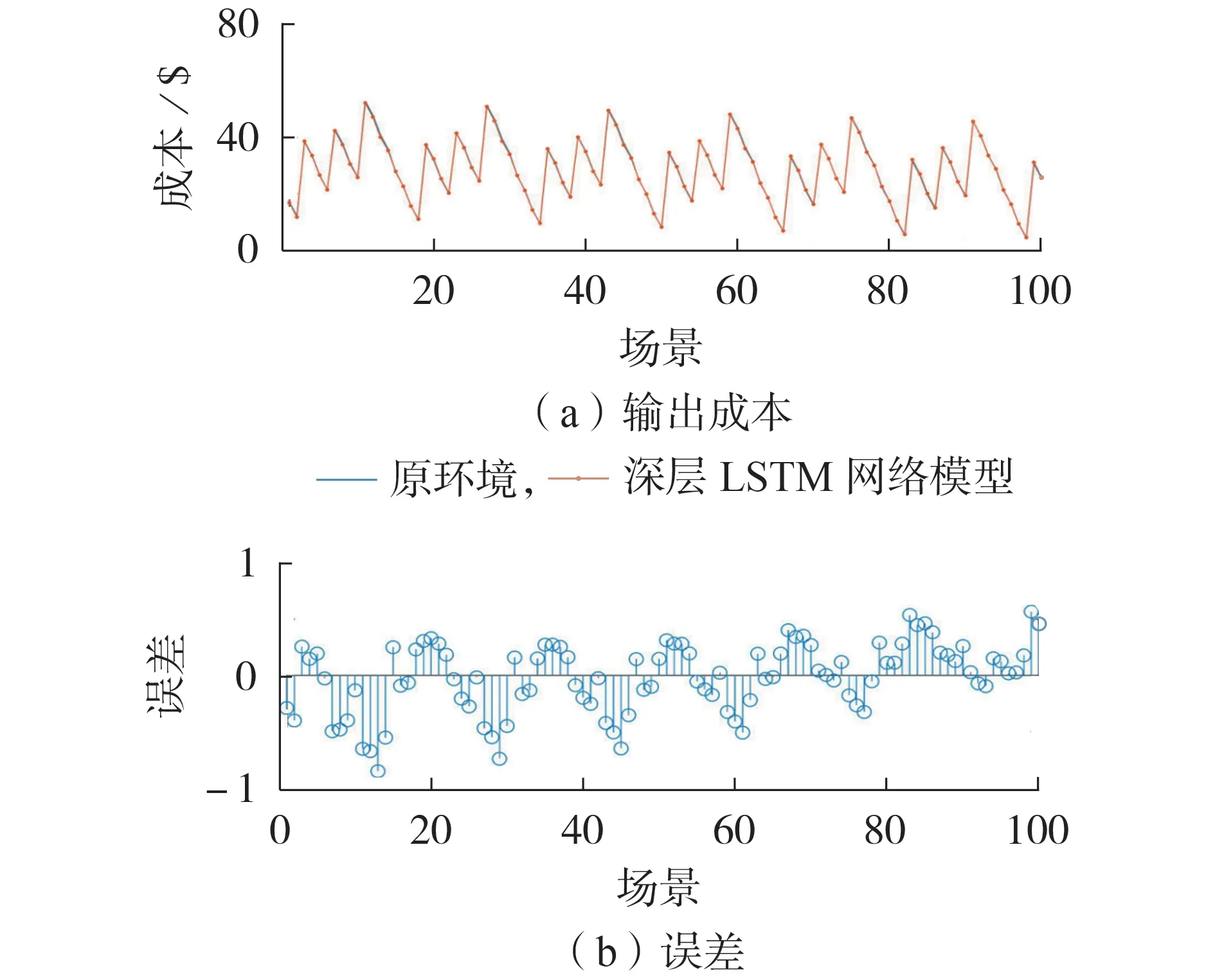
图6 深层LSTM网络误差分析Fig.6 Error analysis of deep LSTM network

表1 进一步对比了SAC 智能体在原环境与深层LSTM 网络所建环境下的离线训练时长以及在线决策的平均成本。从表中可见，深层LSTM 网络所构建的环境减少了80.03%的离线训练时长，而在线决策平均成本仅与原环境相差0.01%。这表明所提深层LSTM 网络环境建模在不影响在线决策精度的前提下，显著减少了智能体的离线训练时长。需要说明的是，尽管智能体的离线训练时间较长，但在在线决策阶段，由于可以直接利用离线训练好的策略网络进行决策，其耗时仅为0.41 s，因而可以满足在线决策的需求。

表1 2种环境模型效果对比Table 1 Comparison of effects between two environment models

4 结论

本文提出了一种基于SAC的微电网源储协同调度策略，得到的主要结论如下：

1）所提方法能够通过不断地与环境进行交互的方式获得最优策略，并基于部分模型信息进行策略搜寻，确保所得策略满足安全约束；

2）所提环境建模方法在不影响策略准确性的前提下，减少了SAC智能体的训练时长，提高了SAC智能体的学习效率；

3）所提方法对模型信息的依赖程度较低，仅用时0.41 s 便可获得显著优于短视策略的解，可以较好地满足微电网源储协同调度的在线决策要求。

附录见本刊网络版（http：//www.epae.cn）。