基于合作博弈的能源互联网经济能效分层协同优化调度

钟永洁，李玉平，胡 兵，张 玮，齐以年，孙永辉

（1. 国电南京自动化股份有限公司，江苏 南京 210032；2. 南京国电南自电网自动化有限公司，江苏 南京 211153；3. 河海大学能源与电气学院，江苏 南京 210098）

0 引言

21 世纪以来，能源是国家发展的基础［1-3］，如何在保证能源利用及供应的可持续性、灵活性和经济稳定增长的同时提升能效等级，促进节能减排，是当今社会共同关注的焦点［2，4-5］。而能源互联网是新一代智慧能源系统，它通过多种能源的源、网、荷、储的统一高效协调、紧密互动和集成协同优化［6-7］，实现多能互补利用，减少对化石能源的依赖与利用，发挥能源梯级利用优势，提高能源的综合利用水平［5，8-9］，从而极大地提高整个能源系统的安全性、灵活性和可靠性，受到国内外的高度关注［2，6，10］。构建能源互联网是提升系统综合能效、促进可再生能源规模化开发利用、提高经济效益、实现节能减排和多能协同供应的有效途径之一，这对推动能源可持续发展具有重要意义［6，10-11］。

目前，国内外综合能源系统（综合能源系统是能源互联网的物理载体）［5-7，11-12］、能源互联网等已步入试点示范和技术验证阶段，重点开展了区域能源互联网、园区型综合能源系统示范项目实践［3，6，13-14］。国内外在能源互联网建模、协同优化方面已经有了一些基础性研究［6，14-15］，主要集中在协同优化调度模型、算法等方面，具体体现如下。①基础架构方面：文献［11］从能源互联网分层管理体系角度出发，提出了基于能量路由器的能源互联网分层分区优化策略；文献［12］提出了综合能源系统上、下层的统一架构模型，上层面向能量传输网络，下层面向配网级能源枢纽；文献［13］提出了综合能源系统的分层结构管理方式，缓解了信息不对称性所带来的需求响应优化决策问题；文献［14］面向城市级能源互联网，探讨了能源互联网多层次、多结构、多维度的特性，并对其“区域自治，全局协调”的分层分区协调控制技术进行了分析。②协同优化方面：文献［15］提出了计及子能源系统协同运行效果的综合能源系统多场景协同优化调度问题，并采用多目标层次规划法处理多目标优化问题；文献［16］针对终端能源互联网特性，提出了相应的能效优化调度模型；文献［17］建立了实用的热电互联多能流系统经济排放多目标协同优化调度模型，并提出了一种两阶段优化法来求解模型；文献［18］提出了含冰蓄冷空调的多能联供微电网多时间尺度优化调度模型，建立了考虑冷热负荷变化的双层滚动优化平抑模型。③博弈论方面：文献［19］建立了主要包含产能基地、系统管理商和综合能源用户三方面主体的斯塔克尔贝博弈和联盟博弈模型；文献［20］提出了由配电系统、配气系统、供热系统和多个能量枢纽组成的区域综合能源系统的运行机制，建立了综合能源系统的主从博弈模型；文献［21］基于不同投资主体的博弈机理分析，提出了基于多主体博弈的电气互联综合能源系统联合规划方法；文献［22］在综合能源系统基础框架和模型的基础上，构建了供需两侧主从博弈模型。

综上所述，已有研究大多是针对某一特定层次的能源互联网架构进行分析建模并进行优化调度的，较多集中在某单一优化运行策略下，相对缺乏分层建模、协同优化分析的研究。因此，有必要根据不同工程场景应用需求进一步提出基于合作博弈的分层协同优化模型与方法，建立架构清晰、完善的园区与区域能源互联网互动的协同优化调度体系。基于此，本文提出了基于合作博弈关系及能量管理系统信息交互原理的能源互联网互动分层协同优化架构、上层及下层模型、优化调度方式和求解流程，同时提出了基于合作博弈的能源互联网分层协同优化调度策略，并进行了仿真验证。

1 园区与区域能源互联网分层架构

能源互联网在地理、调度、管理等方面存在明显的分层结构［1，3，5-6，9］，园区与区域能源互联网互动分层架构如图1 所示。下层园区能源互联网主要面向终端用户侧［9，16］，园区能源互联网工程应用实体如新兴经济开发区、综合商业区、高新技术开发区、工业示范区、大型娱乐中心等，在下层园区能源互联网中，各类型能源转换设备相互协同配合工作，使得多类型能源以最优方式耦合、转换、互动配合；上层区域能源互联网主要以能源传输系统为主［5，10，21］，通常主要包含天然气、电力和热力等多个异构能源系统，各种能源子系统在传输能量的同时也通过大型能源转换设备与其他类型的能源系统进行耦合互联、协调运行工作，如电力系统与热力系统通过电锅炉、热电联供等耦合互联在一起，电力系统与天然气系统通过电转气、热电联供等耦合互联在一起，天然气系统与热力系统通过燃气锅炉、热电联供等耦合互联在一起。下层园区能源互联网与上层区域能源互联网通过能源管理系统进行信息交互，上、下层能源互联网根据调度指令调整系统运行方案。

上层区域能源互联网与下层园区能源互联网在地理位置上通常相距较远，且属于不同的利益主体。下层园区能源互联网面向用户侧，关注园区的整体能效效益，是典型的消费者［3，19］；而上层区域能源互联网面向中、大型能源传输系统，是能源生产、供能方，更关注能源系统整体的经济成本，从供能方的角度而言，在满足下层消费者的负荷需求的基础上，希望供能经济成本最小，即能源传输系统以一种最优的能源供给方式运行。显然上层区域能源互联网与下层园区能源互联网之间存在竞争、矛盾冲突关系，即博弈关系，可以通过一定的博弈策略使得上层区域能源互联网与下层园区能源互联网获得最佳调度方式。

2 园区与区域能源互联网模型和优化调度

本文以图1 所示的园区与区域能源互联网互动分层架构为例，研究基于合作博弈的分层协同优化调度问题。在互动分层架构的基础上，分别建立上层区域能源互联网与下层园区能源互联网模型，并提出能效、经济优化调度策略。

图1 园区与区域能源互联网互动分层架构Fig.1 Hierarchical architecture of interaction between park-level and regional energy internet

2.1 下层园区能源互联网模型与能效优化

2.1.1 主要能源转换设备模型

1）燃气轮机。

计及变工况特性的燃气轮机模型如下［17］：

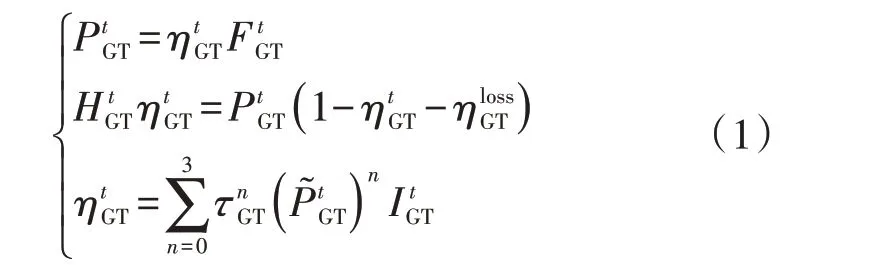
式中：F、P、H、P͂分别为燃料输入量、电功率、热功率、电负载率；η、τ、I分别为效率、多项式系数、表示运行状态的布尔变量，其中设备运行时布尔变量取值为1，设备停机时布尔变量取值为0；n为多项式幂次；上标t、loss 分别表示时刻、能量损失；下标GT 表示燃气轮机。

2）余热回收装置。

余热回收装置回收利用燃气轮机排出的高温烟气进行制热，变工况特性下其模型如下［11］：

式中：下标ACHI表示吸收式制冷机设备。

冰蓄冷空调模型与运行约束见文献［18］。

2.1.2 能效优化调度

能效是园区能源互联网优化调度运行需要重点关注的问题之一，㶲效率不同于一次能源利用率或综合能源利用率从能源数量角度衡量系统的效益，㶲效率是基于不同能源质量差异即品质差异来衡量系统的效益的［5，11，16］。在通常的㶲效率优化调度相关研究中并不考虑输入电能的成分因素，即购电电能中新能源发电的占比、燃煤机组发电的占比、燃气机组发电的占比等，然而实际工程应用场景中，输入㶲值，尤其是购电电能的成分会影响输入㶲的大小，电能来源中各种成分占比不同、各类型发电机组的效率不同、各类型能源的品质不同都会直接或间接地影响㶲效率和上层区域能源互联网各电源的出力情况。

本文提出的日前能效优化调度即考虑㶲效率的优化调度，能效优化调度的目的是获得最大㶲效率，㶲效率定义为系统的输出㶲值与输入㶲值之比［5，16］，下层园区能源互联网日前能效优化调度模型如下：

2.1.3 运行约束条件

下层园区能源互联网日前能效优化调度运行约束主要包括能源转换设备运行约束、各类型新能源出力运行约束、各类型能量平衡约束、联络线功率传输限制约束等。

1）能源转换设备运行约束。

能源转换设备的出力与爬坡能力、优化调度周期内启动次数运行约束如下［7，9-11］：

式（11）为能源转换设备的统一运行约束表示形式，当具体到某一设备不具有某项约束时，该项自动失去意义，如对于锅炉，自动删除式（11）中第1、3、4、6个子式即可。

能源转换设备的最小停机、开机时间约束如下：

3）能量平衡约束。

下层园区能源互联网中涉及冷、热、电、气等多种能量，在优化调度周期内需实时满足电母线、热母线、冷母线、天然气母线能量平衡约束要求，即［7，22］：

式中：下标ISAC表示冰蓄冷空调。

4）联络线功率传输限制约束。

与下层园区能源互联网相连接的配电、配气接口或端口受物理条件限制，其功率交换量受到约束，下层园区能源互联网与上层区域能源互联网联络线或配电站、配气站运行约束为：

2.2 上层区域能源互联网模型与经济优化

2.2.1 主要能源转换设备模型

1）电锅炉。

电锅炉与燃气锅炉的变工况特性类似，其变工况特性模型如下：

式中：下标EB表示电锅炉设备。2）电转气。

电转气过程较为复杂，电转气技术使得电力、天然气能源子系统之间的耦合互动关系愈加紧密，它实现了2 个系统之间能量的双向流动，本文从能量转换整体效率角度出发，建立能量转换模型如下：

上层能源互联网中燃气锅炉模型见式（3），不再赘述。

2.2.2 经济优化调度

上层区域能源互联网经济优化调度成本主要包括弃风惩罚费用和弃光惩罚费用fre、消耗气源天然气费用fGW、热电联供机组消耗燃料费用fCHP、火电机组消耗燃料费用fTU，因此上层区域能源互联网日前经济优化调度模型为：

2.2.3 运行约束条件

上层区域能源互联网运行约束条件主要包括以下约束：能源转换设备运行约束；新能源出力约束；能量平衡约束。具体运行约束形式见2.1.3 节，不再赘述。

因为上层区域能源互联网中的火电机组为电力系统的主要电源，所以电力系统需要满足以下旋转备用约束：

式中：U、D分别为机组的向上、向下旋转备用容量；M、N分别为电力系统的向上、向下旋转备用容量，通常取系统总负荷的5%左右。

基于合作博弈的分层协同优化调度中的下层园区能源互联网购电电能来源于上层区域能源互联网，上层区域能源互联网的电源主要有新能源发电、燃煤发电、燃气发电。不同时刻下购电电能中不同类型能源发电的占比也在变化，不同类型能源发电渗透率约束为：

式中：下标eps表示上层区域能源互联网电力系统中所有类型的发电机组。

3 基于合作博弈的分层协同优化调度求解

3.1 合作博弈模型

3.1.1 多目标优化问题的数学描述

多目标优化问题的数学描述如下［19-21］：

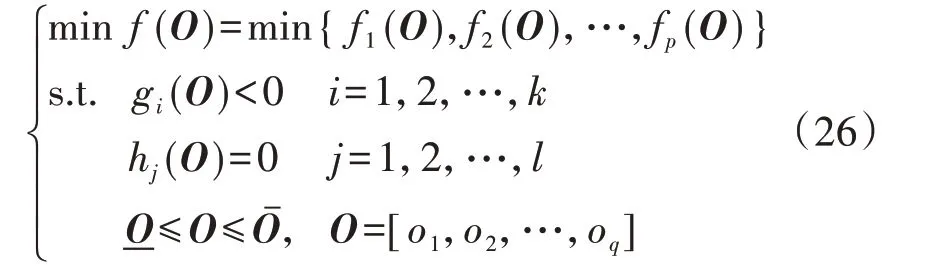
3.1.2 基于合作博弈法求解多目标优化问题

在合作博弈中，各博弈参与方之间以集体理性为基础，追求集体收益最大化的同时使各个博弈参与方满意。因为集体收益与各方的个体收益密切相关，所以要求各博弈参与方在追求自身利益的同时要考虑集体的利益，各博弈参与方需适当控制其个体理性，以集体理性为指导，确保整体收益的增加。

基于此，建立合作博弈模型如下［19-22］：

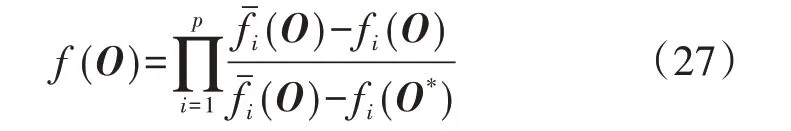
式中：fi(O)为第i个目标函数；fˉi(O)为fi(O)的最不理想值；fi(O*)为fi(O)的最优值。

上述模型恰当地反映了合作博弈中所要求的个体理性与集体理性，通过求解该合作博弈模型，可使各博弈参与方远离自身的最不理想收益，实现收益均衡，同时使合作的整体收益达到最高。

3.2 分层协同优化调度求解

考虑园区能源互联网与区域能源互联网互动的经济能效分层协同优化调度求解及合作博弈基本流程如附录A 图A1所示，合作博弈过程分为外层合作博弈与内层合作博弈，具体步骤如下：步骤1，在外层合作博弈中，下层园区能源互联网能效优化调度与上层区域能源互联网经济优化调度进行博弈，博弈参与方通过能量管理系统进行信息交互；步骤2，外层博弈结束后，确定联络线信息；步骤3，上层区域能源互联网以外层合作博弈结果即确定的联络线信息为基础，进行电力系统经济成本优化与天然气系统经济成本优化博弈，博弈参与方通过能源管理系统交互电源、气源出力信息；步骤4，直至内层合作博弈结束，输出能源互联网优化调度结果；步骤5，如果有新的场景调整变化，可以通过再次调整重复步骤1—4来进行求解。

内层合作博弈过程的电力系统经济成本优化目标与天然气系统经济成本优化目标分别如式（28）、（29）所示，合作博弈模型的求解步骤见附录B。

4 算例分析

4.1 基础数据

本文以图1 所示的园区与区域能源互联网互动分层架构为仿真算例，以冬季典型日为一个仿真周期（即24 h），仿真步长为1 h，冬季典型日中无冷负荷需求，地源热泵以制热工作模式运行，因此图1 中表示供冷能量流路径暂时未启用，并采用附录A 图A1 所示的外层、内层能源互联网合作博弈流程图处理博弈求解过程。在MATLAB 2018a平台进行前期的数据输入、处理及接口搭建，基于通用的商业优化软件LINGO18.0平台编写模型程序并调用全局求解器（Global Solver）进行求解，全局求解器提供全局最优解的选项，不同于一般算法只能获得局部的最优解，其可以通过多起始点的方式，通过划分凸规划，调用分支定界管理程序，从多个局部最优解中确定全局最优解，将非线性模型优化到全局最优解。

下层园区能源互联网中的热负荷、电负荷、气负荷需求以及风电、光伏的预测出力如附录D 图D1所示（在不改变数据且利于直观反应曲线变化趋势的前提下，下文中所述的所有离散的点均用连续的曲线方式呈现），下层主要能源转换设备参数信息如附录D 表D1 所示，其中优化调度周期内环境温度设置为269.15 K；燃气轮机热能损失因子为0.1；余热回收系统效率为0.82，余热回收系统工作状态与燃气轮机配合协调一致组合在一起工作；地源热泵允许的工作时段为［06:00，24:00］，要求停机时段为（00:00，06:00）；根据调度需要下层园区能源互联网可以接受的最大弃风率为60%，最大弃光率为60%；下层园区能源互联网与上层区域能源互联网电能联络线功率交换下限为5 MW／h，天然气联络线功率交换下限为15 MW／h，下层园区能源互联网只允许从上层区域能源互联网购电、购气，不允许反向功率传输。

上层区域能源互联网中的热负荷、电负荷、气负荷需求及风电、光伏的预测出力如附录D 图D2所示，上层主要能源转换设备参数信息如附录D 表D2 所示，其中火电机组有2 台，分别记为1 号TU、2 号TU；1 号TU 的上爬坡速率为50 MW／h，下爬坡速率为50 MW／h，上旋转备用容量为50 MW，下旋转备用容量为50 MW；2 号TU 的上爬坡速率为20 MW／h，下爬坡速率为20 MW／h，上旋转备用容量为20 MW，下旋转备用容量为20 MW；气源出力限值为380 MW／h；弃风惩罚系数设为30$／（MW·h），弃光惩罚系数设为10$／（MW·h）。其他仿真相关参数如附录D表D3所示。

4.2 结果分析

4.2.1 合作博弈下的分层协同优化调度

下层园区与上层区域能源互联网经济能效分层协同日前优化调度结果如表1和表2所示。表中，能效优化调度指下层园区与上层区域能源互联网为一个整体，优化目标为能效优化即下层的㶲效率优化调度，此时购电电能的不同类型能源发电的占比亦为变化量，下层园区与上层区域能源互联网通过联络线数据交互相互耦合在一起；经济优化调度指下层园区与上层区域能源互联网为一个整体，优化目标为经济优化即上层的经济调度，其他情况同能效优化调度；博弈最优折中解指采用合作博弈法，下层园区与上层区域能源互联网在博弈最优折中解方式下的运行情况；文献［10］方法是采用文献［10］介绍的基于调度中心关系的优化运行模式。下层园区能源互联网能效协同优化调度即采用㶲效率最大化模式，在下层园区能源互联网各类型负荷确定的基础上，优化求解㶲效率最大等效于优化求解输入㶲最小。上层区域能源互联网的合作博弈基础为外层合作博弈最优折中解，在上层区域能源互联网中，电力系统经济成本目标与天然气系统经济成本目标进行内层合作博弈，电力系统和天然气系统为不同的利益综合体，经济成本主要考虑各自能源系统在满足正常供能的基础上的能源耗量成本，从上层区域能源互联网的整体角度而言，内层合作博弈是使得区域能源互联网的运行经济成本最低。

表1 外层合作博弈下的协同优化调度结果Table 1 Collaborative optimal scheduling results under outer cooperative game

表2 内层合作博弈下的协同优化调度结果Table 2 Collaborative optimal scheduling results under inner cooperation game

根据表1 可知，在外层合作博弈过程中，下层园区能源互联网能效协同优化调度的最优结果为0.487 7294，上层区域能源互联网经济协同优化调度最优结果为$332 049.9，外层合作博弈的最优折中解均略微次于对应的单一能效优化和经济优化的结果。外层合作博弈的最优折中解的结果相较于能效优化效率降低了0.8%，相较于经济目标值提高了2.2%，可见其幅度均不大，但是合作博弈最优折中解却兼顾了能效优化与经济优化这2 个因素，使得下层园区与上层区域能源互联网均获得了理想的满意解。外层合作博弈最优折中解与文献［10］所提的优化调度方法相比，能效目标值由0.476 622 9增加至0.483 584 1，提高了1.46%，经济目标值由$339 759.6 减少至$339 384.4，降低了0.1%。文献［10］是基于调度中心的关系进行分层协同优化的，而基于合作博弈的分层协同优化进一步考虑了上、下层之间的利益冲突和矛盾，与文献［10］中协同优化调度结果相比，基于合作博弈的方法取得的最优折中解更好。

根据表2 可知，在内层合作博弈过程中，由于合作博弈双方均为经济成本目标，合作博弈相对于单一的电力系统经济成本优化、天然气系统经济成本优化而言博弈最优折中解均较大，然而最优折中解的结果平衡了电力系统经济成本优化与天然气系统经济成本优化，使得博弈双方均获得一个满意解。与文献［10］方法相比，内层合作博弈的最优折中解电力系统成本值减少了$14 280.95，经济成本降低了19.9%，而天然气系统成本值增加了$18040.5，经济成本提高了6.7%，总成本值提高了1.1%，其增幅较小。与文献［10］方法相比，内层合作博弈最优折中解中博弈参与方的目标值有较大变化，可见基于合作博弈法的协同优化调度在有效地平衡冲突方利益的同时也使得总体利益不会发生较大变化。

4.2.2 外层与内层合作博弈Pareto前沿分析

基于合作博弈的下层园区与上层区域能源互联网的经济能效分层协同优化调度的外层合作博弈Pareto 前沿如图2 所示，内层合作博弈Pareto 前沿如图3所示，均布搜索可行空间Pareto解集个数下的外层、内层合作博弈的联盟收益分别如附录E 图E1、E2 所示。由图2 可知，上层区域能源互联网的经济成本与输入㶲之间存在一系列的可行解，最优折中解对应的输入㶲为1872.634 MW·h，经济成本为$339384.4，同时对应的㶲效率为0.4835841。在工程实际应用中，上层区域能源互联网和下层园区能源互联网可以采用合作博弈最优折中解的方案进行优化调度，对于不同的工程应用场景需求，不同的协同优化调度运行方案均可以在Pareto 前沿上找到对应的方案。

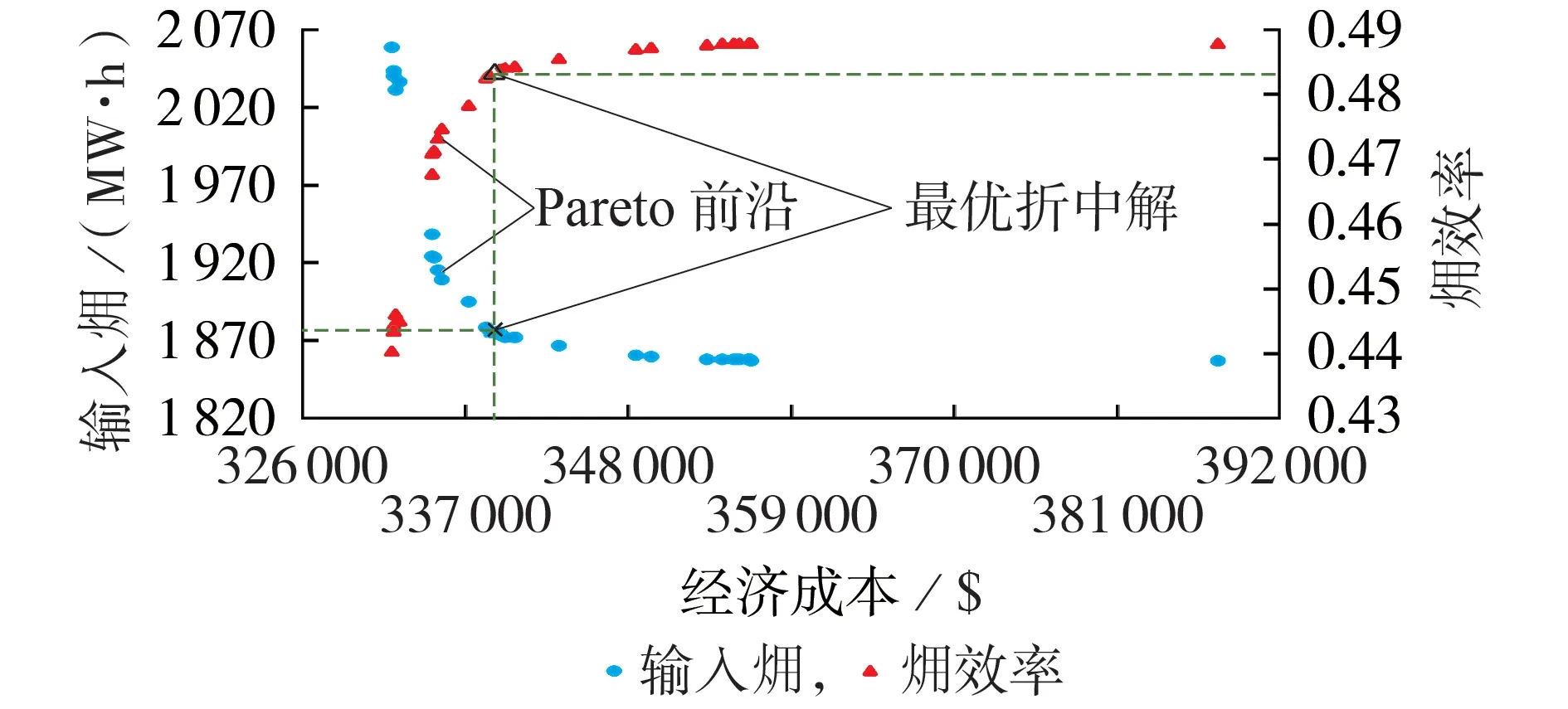
图2 外层合作博弈Pareto前沿Fig.2 Pareto frontier of outer cooperation game

图3 内层合作博弈Pareto前沿Fig.3 Pareto frontier of inner cooperation game

由图2 可以看出，在一个优化调度周期内，能效优化调度的㶲效率上限不超过0.49，下限不低于0.43，㶲效率取值集中在0.48 左右，与此同时对应的输入㶲集中在1 870 MW·h 左右，对应的经济成本集中在$339000.0左右。偏离合作博弈最优折中解对应方案的调度运行势必会导致能效或㶲效率性能变差，如使得上层园区经济成本降低会促使㶲效率急剧降低，反之结果类似。根据图3，总经济成本与电力系统经济成本之间存在二次函数的关系，在博弈的过程中，总经济成本有最小值，而图3 所示的合作博弈结果表明，最优折中解对应的点不是总经济成本的最小值。内层合作博弈的参与方为电力系统经济成本与天然气系统经济成本，博弈的效果是平衡、兼顾两者的利益，并不是单一地追求上层区域能源互联网总经济成本最小，当然上层区域能源互联网的总经济成本已经在外层合作博弈予以考虑，内层合作博弈正是在外层合作博弈的基础上进行的。结合表1 所示的结果，内层合作博弈与外层合作博弈对应的经济成本最优折中解是不相同的，结果表明增加内层合作博弈可以使得系统运行方式得到进一步优化。

4.2.3 不同运行模式下的能效经济动态变化特征

不同运行模式下的下层园区能源互联网㶲效率动态变化如图4所示。

图4 不同运行模式下的㶲效率动态变化Fig.4 Dynamic variation of exergy efficiency under different operating modes

根据图4 可以明显发现，在单一的经济优化调度运行模式下，㶲效率整体上均较低，在单一的能效优化调度运行模式下，㶲效率整体上均较高，而在博弈最优折中解的运行模式下，㶲效率整体上与能效优化调度变化趋势相同且非常接近。采用文献［10］的优化调度运行模式时下层园区能源互联网的㶲效率波动幅度相对较大。根据图4，在整体优化调度周期内单一经济优化调度运行模式下㶲效率相对较低，其他3 种运行模式尤其是在01:00—07:00 和19:00—24:00 时段的㶲效率非常接近，可见在优化调度周期内，不同运行模式下的㶲效率变化既有相同点也有不同点。结合表1 所示的外层合作博弈的结果，虽然经济优化调度使得上层区域能源互联网的经济成本最低，但是经济效益较好的前提是以牺牲㶲效率为代价的，在实际工程应用中显然需要顾及下层园区能源互联网的㶲效率利益，系统采用外层合作博弈下博弈最优折中解的运行方式可以平衡、兼顾上层和下层能源互联网效益。

不同运行模式下的上层区域能源互联网经济成本动态变化如图5 所示，图中电力系统优化和天然气系统优化指在外层合作博弈结果上进行单一的经济成本优化调度，外层合作博弈后获得联络线数据信息，将外层合作博弈得到的最优折中解下所对应的联络线数据信息通过能量管理系统交换上传到上层区域能源互联网中，而经济优化对应图4 中的经济优化调度运行模式。

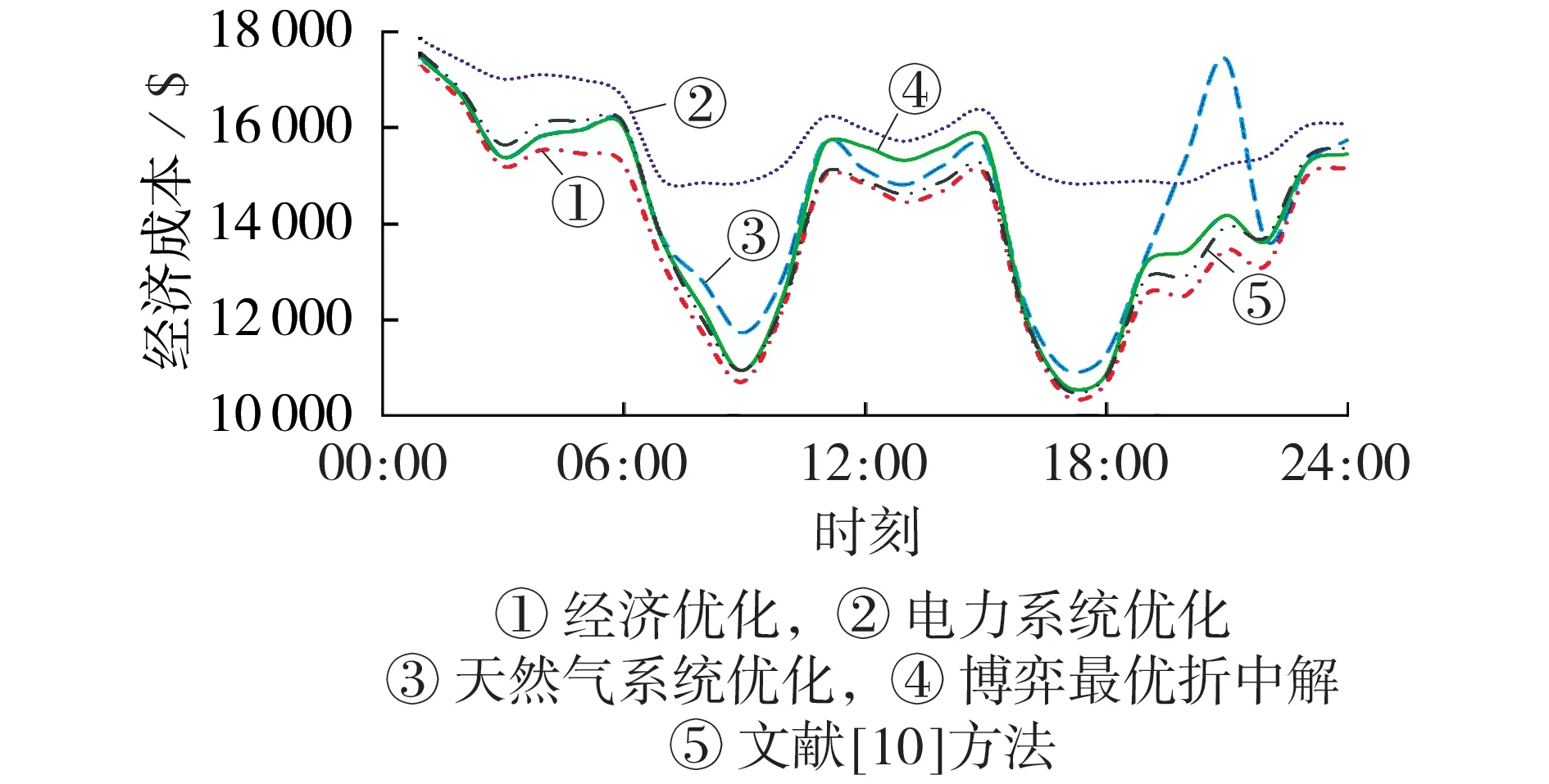
图5 不同运行模式下的经济成本动态变化Fig.5 Dynamic variation of economic cost under different operating modes

根据图5 所示的优化结果，在电力系统优化模式下上层区域能源互联网经济成本最高，在经济优化运行模式下经济成本最低，在天然气系统优化运行模式下经济成本波动幅度最大。对比电力系统优化、天然气系统优化、经济优化运行模式的结果可以看出，不同运行模式下上层区域能源互联网经济成本差异较大，单一地追求电力系统效益或天然气系统效益都是不合理的，而在博弈最优折中解的运行模式下经济成本总体均较低，且接近经济优化运行模式。结合表1和图5可以看出，采用文献［10］的运行模式也可以使得上层区域能源互联网经济成本较低且与博弈最优折中解的运行模式下的结果相接近，但博弈最优折中解的运行模式考虑了上层区域能源互联网不同利益方的经济成本效益，考虑的因素更为全面。

5 结论

在基于合作博弈的分层协同优化调度方面，本文介绍了园区能源互联网与区域能源互联网互动分层基本架构，并在建立下层园区与上层区域能源互联网模型的基础上，构建了下层园区能源互联网日前能效优化调度模型、上层区域能源互联网日前经济优化调度模型，给出了基于合作博弈的分层协同优化调度求解流程，进一步地通过算例分析验证了基于合作博弈的分层协同优化模型及方法的合理性、优越性。研究表明：本文所提模型与方法综合考虑了能源互联网的互动分层特征，更加符合工程应用场景，有利于降低优化调度经济成本，提高综合能效水平；从经济、能效角度考虑能源互联网优化调度的多重需求，更能满足不同优化调度模式下的利益需求；基于合作博弈考虑能源互联网不同层次方的追求，有利于平衡各方利益冲突与矛盾。

附录见本刊网络版（http：//www.epae.cn）。