基于自适应不完全S变换与LOO-KELM 算法的复合电能质量扰动识别
伊慧娟,高云鹏,2,朱彦卿,黄 瑞,2,3,黄 纯
(1. 湖南大学电气与信息工程学院,湖南 长沙 410082;2. 智能电气量测与应用技术湖南省重点实验室,湖南 长沙 410004;3. 国网湖南省电力有限公司,湖南 长沙 410004)
0 引言
近年来,随着光伏、风力发电等新能源分布式电源并网行为的增加,新型电力电子器件与设备不断接入,引起大量复杂且次数频繁的稳态与暂态电能质量扰动,此类复合电能质量扰动(下文简称复合扰动)的特征混叠严重,相对于单一电能质量扰动(下文简称单一扰动)识别,复合扰动识别对特征提取与分类器选择的要求更高,因此如何针对复合扰动的特点进行准确、高效的复合扰动识别成为当前电能质量扰动分类研究的重要课题[1]。
复合扰动识别主要包括特征提取与模式识别2个步骤。特征提取需对信号进行时频域分析,常用的方法有傅里叶变换[2]、小波变换[3]、S 变换[4]等,其中S 变换结合傅里叶变换与连续小波变换的优点,引入窗宽可调的高斯窗函数,在时、频域均具有分析能力,在单一扰动特征法的提取中得到了广泛应用,但当前智能电网环境下存在较多单一扰动叠加的复合扰动,对S 变换的时频域分辨率及特征提取效率的要求更高。文献[5-6]通过S 变换获得具有高时频分辨率的复合扰动时频特征,但在不完全S 变换中,实现高时频分辨率的窗宽因子需通过大量实验进行确定,特征提取效率低、成本高。复合扰动模式识别方法主要包括专家系统[7]、人工神经网络、支持向量机[8]、决策树[9]、深度学习[10]、极限学习机等,其中专家系统分类器过度依赖先验知识;人工神经网络分类的过程为“黑盒”,训练时间长;支持向量机计算速度快,但需解决核参数优化选择问题;决策树的分类精度较高,但需对参数进行调节,易出现过拟合的问题;深度学习的分类精度高但需大量样本且训练时间过长,上述分类器均存在难以实现训练时间与测试精度同步提高的问题。随着复合扰动在电能质量扰动中占比的增加,研究快速、准确性高、专家依赖度低且参数设置简单的分类器在工程应用中逐渐得到重视。核极限学习机KELM[11](Kernel Extreme Learning Machine)为前向传播神经网络,其输入层与隐含层间的连接权值直接被设定且在后期训练过程中无需调整,在大幅提高了算法效率的同时,保证了较高的识别精度。目前已有研究通过粒子群优化PSO(Particle Swarm Optimization)算法[12]等对KELM的正则化参数进行优化,但均以分类器准确度作为适应度函数,优化过程复杂冗长。
针对上述问题,本文首先利用基于特定选择频率的自适应窗宽因子改进不完全S 变换(简称自适应不完全S 变换),得到高时频分辨率的复合扰动特征集,再通过基于预测残差平方和的留一交叉验证LOO(Leave-One-Out cross validation)法得到KELM的正则化参数,据此建立基于自适应不完全S 变换与LOO-KELM 算法的高效复合扰动特征提取与识别方法,最后通过大量仿真和实测数据验证本文所提方法的有效性和准确性。
1 基于自适应不完全S变换的特征提取
S 变换采用窗宽与窗高可随频率自动调节的高斯窗函数,在时频域对信号进行分解。复合扰动信号为离散信号x(n),因此采用离散S 变换进行信号分析,其表达式为:

式中:σf为高斯窗的窗宽调节因子:a0、a1、b1、w为常数;f为频率。
复合扰动可解耦至低、中、高3 个频段,且主要集中在几个特定频率处,因此在特定频率处采用不完全S变换,可显著降低S变换矩阵的获取时间。结合电能质量扰动的定义与扰动信号的快速傅里叶变换FFT(Fast Fourier Transform)结果可知,暂降、暂升、中断、闪变对电压幅值造成的影响较大,但电压频率基本不受影响,因此对上述扰动在50 Hz 处进行频域特征提取;谐波主要包括3、5、7、9 次奇次频率成分,其他频率点的谐波幅值基本为0;由振荡信号的定义可知,其信号中心频率集中在300~900 Hz,通过FFT 可知其频域中心点与250、350、450、550、650、750、850、950 Hz 接近,为快速得到信号在频域的特征,选择以上相近频率点作为特征频率点。
对上述不同频率段的多个电能质量扰动信号进行分解,调整窗宽因子使分解结果具有较高的时频分辨率,由多次实验确定的不完全S变换的σf计算式为:
σf=9.7-9.5 cos(0.15f)-1.95 sin(0.15f) (5)
在选取的分解频率下,由式(5)得到的不完全S变换的窗宽因子见附录A 表A1。由表可知,在不完全S 变换的特征提取中,只需设定好进行分析的频率位置,利用式(5)得到的窗宽因子即可动态调整高斯窗函数,由此得到具有高时频分辨率的扰动特征。
暂降+谐波信号和暂降+振荡信号这2种复合扰动信号的FFT结果分别如图1(a)、(b)和图2(a)、(b)所示,对应的自适应不完全S 变换时频分析结果分别如图1(c)和图2(c)所示。
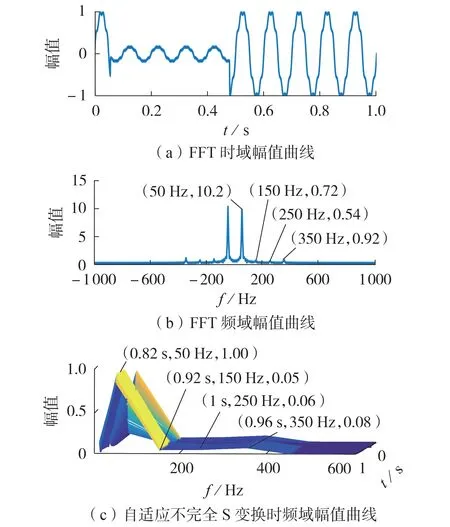
图1 暂降+谐波信号的FFT结果和自适应不完全S变换结果Fig.1 FFT and self-adaptive incomplete S transform results of sag+harmonic signal

图2 暂降+振荡信号的FFT结果和自适应不完全S变换结果Fig.2 FFT and self-adaptive incomplete S transform results of sag+oscillation signal
由图1(a)可见,暂降+谐波信号在时域呈现明显的电压降落现象;由图1(b)可见,FFT 频域幅值曲线的最高峰在50 Hz 处,该复合扰动信号中除了基频外还包含3、5、7 次谐波,频率成分主要为50、150、250、350 Hz,结合图1(c)可知,自适应不完全S变换和FFT得到的频域分析结果相同。由图2(a)可见,暂降+振荡信号在时域的电压降落较为明显;由图2(b)可见,信号包含50 Hz 的基频与振荡中心为440 Hz 的高频;由图2(c)可见,频率50 Hz 处为时频幅值曲线的最高峰,即信号频率成分主要为基频;时频幅值曲线的次高峰出现在450 Hz,即信号除基频外还包含部分高频成分,与图2(b)中的结果基本吻合。综上所述,本文提出的自适应不完全S 变换对各个频段的电能质量扰动信号均具有良好的时频分辨率,可有效提取频域信息。将进行不完全S 变换后的幅值矩阵记为Ts,根据Ts的行、列向量构建电能质量特征[13],最终得到的59 种电能质量特征值见附录A表A2。
2 LOO-KELM算法
2.1 KELM
极限学习机ELM(Extreme Learning Machine)是一种基于单向前馈神经网络架构的新型快速学习算法,其隐藏层的节点参数在给定的随机范围内初始化,无需进行复杂的参数调整计算。KELM[14]是ELM的新型改进方法,需要设置的参数更少,无需提前设置隐藏节点,涉及的核参数为随机产生,训练速度快且泛化能力更强。KELM 分类器可在保证分类精度的情况下,实现复合扰动模式的快速识别。
给定复合扰动样本数量为Z、扰动模式总数为M的复合扰动训练样本集(xi,ti),其中xi为进行学习的特征数据集,ti为特征数据集对应的分类标签,i=1,2,…,Z。设置ELM 网络的隐藏节点数为u,选用的激活函数为s(x),其输出结果可表示为:

式中:γ为RBF核参数。

式中:T为分类标签组成的矩阵。
由此可知,KELM 通过加入正则化系数平衡训练误差项与正则化项,从而提高复合扰动分类结果的稳定性。
2.2 改进LOO法
LOO 法是常见的交叉验证法,其将样本数据集划分为2 个子集,其中一个子集为验证集,仅包含1个样本,用于模型的泛化误差验证;另一个子集为训练集,用于模型的训练。样本数据集的划分一直持续到每个样本均作为验证集进行误差验证为止,得到各个留一验证集的平均泛化误差,泛化误差越小则分类器的实际分类性能越好。通过LOO 法优化KELM 分类器的参数,可进一步提高电能质量扰动模式识别精度(下文简称扰动模式识别精度)。对于包含Y个样本的复合扰动训练集,利用其中的Y-1个样本进行训练,剩余的1 个样本用于对训练模型进行泛化性能评估。通过统计量预测残差平方和PRESS(Predicted Residual Error Sum of Squares)线性模型代替多重重复训练模型,降低KELM 分类器中正则化系数计算的复杂度,从而以较低的时间成本提高扰动模式识别精度。

基于均方误差MSE(Mean Square Error)的PRESS计算式中:HNEWii为矩阵HNEW对角线上的第i个元素值;verri为第i个样本数据与其标签的预测残差平方值;f′outfiti为第i个样本经过KELM 网络后的输出值;ferr(•)为PRESS计算函数。
将式(7)代入式(13),可得KELM的HNEW为:

传统的LOO 法在优化正则化系数C时,需要对KELM 进行Y次重复训练,其计算复杂度为O(Y2),本文通过预测残差平方和的线性模型代替原始的LOO 模型,只需一次性计算出ΩELM与(ΩELM+I/C)-1,即可以通过式(11)、(12)、(14)计算得到验证误差值,避免了Y次KELM 的训练过程,计算复杂度降低至O(Y)。由此可见,改进的LOO 法大幅缩短了KELM分类器的优化时间,在提高扰动模式识别精度的同时,减少了优化过程引起的时间成本,实现了高效准确的复合扰动识别。为便于说明,下文将经改进LOO法优化的KELM分类器简称为LOO-KELM分类器。
3 复合扰动识别流程
通过自适应不完全S 变换提取复合扰动波形的时频域特征,构建复合扰动特征矩阵,通过求解PRESS 降低LOO 法的复杂度,从而快速优化KELM分类器的正则化系数C。基于自适应不完全S 变换与LOO-KELM算法的复合扰动识别流程如下。
1)通过复合扰动的数学模型产生样本数量为Z的数据集(xi,ti)(i=1,2,…,Z),通过自适应不完全S变换对数据集进行特征提取。
2)将得到的特征数据集按需求分为训练集与测试集,并对样本进行乱序处理,同时将每个样本对应的分类标签进行离散化表示,初始化正则化系数序列,序列长度为L,序列中各元素均在[Cmin,Cmax]范围内,C(p)为序列中第p个元素,p=1,2,…,L,且p初始化为1。
3)将C(p)代入式(11),从而得到KELM 的输出值f′outputi,通过重复利用核矩阵ΩELM提高改进的LOO法的效率,优化的LOO法的目标函数即为式(12)。
4)若迭代次数小于L,则令p=p+1,然后返回步骤3),继续进行迭代寻优;若迭代次数达到L,则迭代结束,转至步骤5)。
5)以最小化目标函数式(12)为目的,得到最优正则化系数Copt,最终得到LOO-KELM 算法的最优输出权重βopt为:

6)将自适应不完全S 变换的提取特征输入LOO-KELM分类器中,得到复合扰动的分类结果。本步骤中KELM 分类器通过寻找输出矩阵中的最大值确定扰动所属类别,该最大值可直接反映分类器的最大决策边界,而样本输出矩阵中的最大值f′output,max与次大值f′output,smax之差Tdiff=f′output,max-f′output,smax可反映决策边界优劣程度,且Tdiff值越大,分类器的决策边界越好,分类精度越高,因此可通过Tdiff值来判断KELM分类器对复合扰动的分类效果。
经过改进LOO 法优化前、后的KELM 分类器的Tdiff值如附录A 图A1 所示。由图可知,优化前,KELM 分类器的Tdiff值主要分布在(0,1.8)范围内,优化后,KELM 分类器的Tdiff值呈现集中分布的特性,且主要分布在(1.8,2.5)范围内,可见经过改进LOO法优化后的KELM 分类器具有较大的Tdiff值,即具有相对较优的决策边界。
4 算例仿真
4.1 仿真模型与样本建立
为验证LOO-KELM 算法的鲁棒性与准确性,根据IEEE Std 1159—2019[15]标准对各种电能质量扰动模式的定义构建电能质量扰动信号的数学模型,通过MATLAB仿真实验生成参数随机且信噪比SNR(Signal Noise Ratio)分别为20、30、40、50 dB 的正常信号(D1)和16 种电能质量扰动信号。其中,电能质量扰动信号包括电压暂降(D2)、电压暂升(D3)、电压中断(D4)、暂态振荡(D5)、电压切口(D6)、电压尖峰(D7)、闪变(D8)、谐波(D9)、暂降+谐波(D10)、暂升+谐波(D11)、闪变+谐波(D12)、中断+谐波(D13)、暂降+闪变(D14)、暂升+闪变(D15)、暂降+振荡(D16)、暂升+振荡(D17),复合扰动信号的数学模型见附录A 表A3。将信号的采样频率、采样点数分别设置为6 400 Hz、1 280。每种信号包含200 组数据,共3 400 组数据,其中2 500 组用于分类模型训练,剩余900 组用于模型测试,并对原本相同模式扰动信号聚类在一起的数据集进行乱序处理,将单一扰动与复合扰动信号随机混合后进行分类实验。
4.2 基于LOO-KELM算法的复合扰动模式识别
由仿真得到2 500 组混合扰动信号对LOOKELM 分类器进行训练,正则化系数C的寻优结果如图3所示。

图3 正则化参数的寻优结果Fig.3 Optimization results of regularization parameter
由图3可见,λPRESSMSE的最小值为0.8896,对应的最优正则化系数Copt=0.027 32,从而可得到LOO-KELM算法的最优输出权重,通过此权重构建最优LOOKELM分类器。
分别对信噪比20、30、40、50 dB 下的复合扰动数据集进行训练与测试,得到最优LOO-KELM 分类器对17种信号的识别精度如表1所示。表中,r为信噪比。
由表1 可知,LOO-KELM 分类器对单一扰动模式,如谐波、闪变、暂态振荡均具有高抗噪能力与高识别精度,因此当这3 种单一扰动叠加电压暂升、电压暂降形成复合扰动时,LOO-KELM 分类器对其仍具有良好的识别精度;LOO-KELM 分类器在不同信噪比下对暂升+谐波、闪变+谐波、中断+谐波这3 种复合扰动模式的识别精度均达了100%,对暂降+振荡扰动在20 dB信噪比下的识别精度为90.74%。综上所述,LOO-KELM 分类器在不同信噪比下对复合扰动模式的识别精度均能保持在90%以上;除电压切口、电压尖峰与电压暂降模式外,LOO-KELM 分类器对其他电能质量扰动模式的识别精度在20 dB 的信噪比下均可达90%以上,这是因为高噪声环境造成的电压切口、电压尖峰扰动信号失真严重,从而对扰动模式识别精度产生了较大的影响,但在实际情况下,电压切口与尖峰出现的频率较低;在40 dB 及以上信噪比的噪声环境中,LOO-KELM 分类器对正常信号和16种电能质量扰动信号的平均识别精度可以达到97%以上,在低信噪比的环境中,平均识别精度也可达到93%以上。由此可见,LOO-KELM 分类器在不同信噪比下均具有良好的分类精度和抗噪性能。

表1 不同信噪比下的最优LOO-KELM分类器对信号的识别精度Table 1 Signal recognition accuracy of optimal LOO-KELM classifier under different SNRs
4.3 与常用复合扰动模式识别方法的对比
在20~50 dB 的信噪比环境下,对比支持向量机SVM(Support Vector Machine)、KELM、PSO 算法改进的KELM(PSO-KELM)、遗传算法改进的KELM(GA-KELM)及本文方法对包含单一扰动与复合扰动的复杂混合扰动的识别效果,各算法的平均训练时间tr和平均扰动模式识别精度rrec如图4所示。
由图4中的上图可见,基于KELM方法的平均训练时间基本不受噪声因素的干扰,其中PSO-KELM、GA-KELM 方法的平均训练时间在300 s 附近波动,而本文方法的平均训练时间在10 s 附近小范围浮动,与PSO-KELM、GA-KELM 方法的平均训练时间相比降低了97%,且基本不受叠加噪声的影响。

图4 不同信噪比下各方法的平均训练时间和平均扰动模式识别精度对比Fig.4 Comparison of average training time and average disturbance mode recognition accuracy among different methods under different SNRs
由图4 中的下图可见,与其他方法相比,本文方法在各种信噪比下的平均扰动模式识别精度均在90%以上,在平均训练时间显著降低的情况下仍可达到96.1%;在20 dB 的低信噪比下,本文方法可保持93.6%的平均扰动模式识别精度,而KELM 与SVM方法的平均扰动模式识别精度只能达到82.3%,PSO-KELM 与GA-KELM 方法的平均扰动模式识别精度也未超过90%。
综上所述,本文方法在不同信噪比下均具有较高的平均扰动模式识别精度,且精度变化幅度最小,尤其在低信噪比条件下展现出良好的抗噪能力与鲁棒性,实现了分类精度与学习速度的同步提高。
5 实测信号分析
为验证本文方法对实测信号的有效性,利用本文方法对广东某电网2020年5月的实测混合扰动信号进行扰动分类。实测信号的采样频率为6.4 kHz,广东某电网2020 年5 月11 日发生暂降+振荡的扰动事件时,三相电压实际波形的PQDiffractor 显示见附录A 图A2。对实测信号进行自适应不完全S 变换,得到的幅值、频率信息如附录A 表A4 所示,表中同时给出了实际扰动事件发生时实测信号本身的幅值、频率信息作为对比。由表可见,自适应不完全S变换可以在除振荡之外的扰动发生时100%准确提取实测信号的所有频率成分,对于发生振荡时的实测信号可提取到与实际振荡中心最相近的特定频率450 Hz处的特征信息。
实测信号数据集由1 000 组训练集与600 组测试集组成,共包含10 类扰动事件。利用本文方法对实测扰动信号数据集进行扰动模式识别,结果见表2。
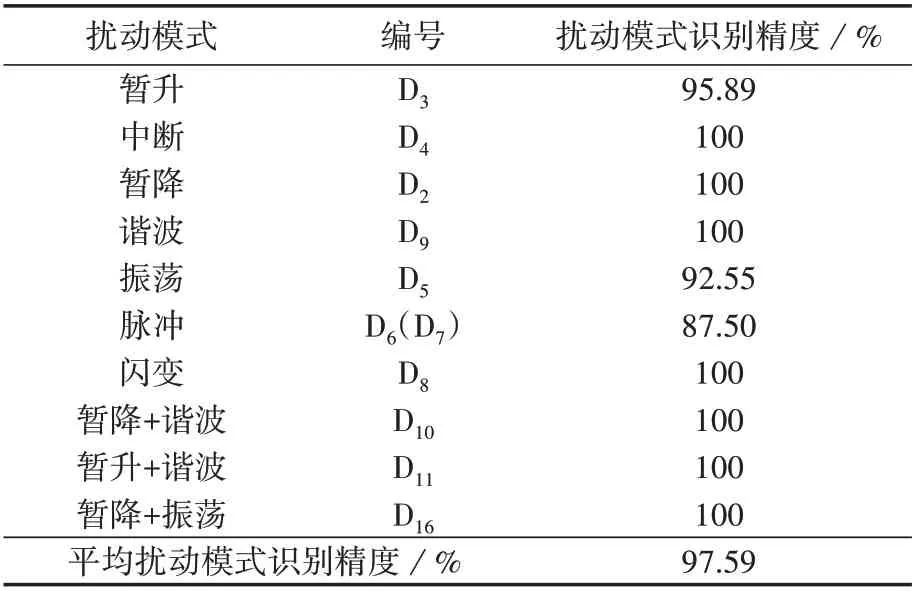
表2 对实测信号数据集的扰动事件识别结果Table 2 Disturbance mode recognition accuracy of identification results of actual signal data set
由表2 可见,本文方法对实际扰动事件的平均扰动模式识别精度达97.59%,对实测信号数据集中的暂降+谐波、暂升+谐波、暂降+振荡这3 类复合扰动模式的识别精度达100%,且通过实测数据进行模型训练的时间仅为12.156 s。由此可知本文方法可快速实现电网的复合扰动模式的精确识别,在实际电网环境下具有良好的复合扰动识别效果。
6 结论
本文提出了一种基于自适应不完全S 变换与LOO-KELM 算法的复合扰动识别方法,通过仿真与实测信号分析结果可得到以下结论:
1)本文方法可对多个选定变换主频率点的窗宽因子进行自适应设置,大幅降低了特征提取时间,同时保证了特征在时频域的分辨率;
2)本文方法对KELM 的输出权重进行优化,在各种噪声环境下均能得到较高的扰动模式识别精度,对实测数据的平均扰动模式识别精度可达到97%以上;
3)与其他复合扰动模式识别方法相比,本文方法的计算复杂度低、训练时间短、扰动模式识别精度,且具有良好的抗噪性。
本文方法的不足在于当信号处于高噪声环境中时,电压尖峰与电压切口这2类扰动模式的信号失真较为严重,因此其扰动模式识别精度会受影响,后续工作需进一步提升高噪声下全扰动模式识别精度。
附录见本刊网络版(http://www.epae.cn)。

