发输电系统鲁棒优化规划研究综述与展望
袁 杨,张 衡,程浩忠,柳 璐,张啸虎,励 刚,张建平
(1. 上海交通大学电力传输与功率变换控制教育部重点实验室,上海 200240;2. 国家电网有限公司华东分部,上海 200120)
0 引言
发输电系统优化规划涵盖了电源规划、输电网规划、机组组合、备用优化及无功优化等研究内容,是电力系统规划与运行的重要组成部分。发输电系统优化规划系列问题在数学本质上均可归纳为形式相似的最优化问题。本文所述的发输电系统优化规划问题集中在学术研究较为丰富的输电网规划、电源规划与机组组合3类问题,围绕鲁棒优化在此3类问题的应用进行综述与展望。
近年来,电力系统源、网、荷各环节的不确定性与日俱增。在电源侧,可再生能源出力具有随机性、间歇性、波动性,难以精准预测;电源的投建、退役以及投资运行成本受经济政策影响,不完全与预期相符。在输电网侧,自然灾害、极端天气或者人为破坏造成了输电线路故障的不确定性;此外输电线路的最大传输容量与所处环境紧密相关,也具有不确定性。在负荷侧,社会经济发展水平与电力市场运行调节手段都会造成用电负荷偏离预期值。在此背景下,研究含不确定性的发输电系统优化规划问题具有重要的学术价值和现实意义。
从数学本质上看,含不确定性的发输电系统优化规划可以分为随机优化、多场景优化、模糊优化以及鲁棒优化。鲁棒优化的求解结果能够适应最恶劣场景,鲁棒优化规划已发展为解决含不确定因素发输电系统优化规划问题的重要方法。文献[1-2]综述了鲁棒优化在发电调度、输电网规划中的应用,文献[3]综述了分布鲁棒优化在电力调度中的应用,文献[4]从概率密度、矩信息及基于这两大类的分布鲁棒机会约束方法角度,提炼了分布鲁棒优化在电力系统应用的共性。虽然现有综述对鲁棒优化在电力系统的规划或运行问题的应用进行了深入梳理,但是存在以下2 点局限:①聚焦鲁棒优化在规划/运行、发电/输电环节的应用,难以全面归纳鲁棒优化在发输电系统优化规划的应用方式;②分布鲁棒优化是鲁棒优化的重要分支,近年来在发输电系统优化规划的应用已愈发广泛深入,相关综述侧重分布鲁棒优化在调度中的应用,对在输电系统规划中的应用涉及相对较少,并且分布鲁棒优化在源、网、荷各环节应用情况的差异性有待总结。
因此,本文将发输电系统鲁棒优化规划研究分为考虑节点注入功率不确定性、电源容量增长及成本不确定性、输电网络状态不确定性3 类,比较分析了每一类中经典鲁棒和分布鲁棒优化的应用发展脉络和值得深入研究的关键问题,以帮助研究人员详实地了解相关研究进展,厘清现有研究思路,提供后续研究方向。
1 鲁棒优化问题的数学模型
鲁棒优化的数学模型有多种分类角度。按照是否计及不确定因素概率分布特征,可分为经典鲁棒优化和分布鲁棒优化。限于篇幅,本文主要综述单阶段经典鲁棒优化、两阶段经典鲁棒优化、单阶段分布鲁棒优化和两阶段分布鲁棒优化数学模型,其余数学模型可参考文献[5]。
1.1 单阶段经典鲁棒优化
单阶段经典鲁棒优化适用于在不确定参数的实现前进行决策的问题,其优点在于形式相对简单,较易求解,缺点在于决策过于保守[6],表达式见式(1)。

式中:x为决策变量;X为决策变量可行域;u为不确定参数;U为不确定参数所属的不确定集合;f为单阶段经典鲁棒优化的目标函数;hj为单阶段经典鲁棒优化的约束条件;m、j分别为约束条件总数和序号;max、min分别为取最大值、最小值函数。
1.2 两阶段经典鲁棒优化
两阶段经典鲁棒优化适用于在不确定参数实现前、后2 个阶段分别确定部分决策变量的问题。与单阶段经典鲁棒优化模型相比,两阶段经典鲁棒优化的优点在于决策者可以在获取不确定参数的取值后调整第2 阶段决策,在保证鲁棒性的前提下降低了保守性,但也增加了求解复杂性[6],其典型形式见式(2)。

式中:y为第2 阶段决策变量;Y为第2 阶段决策变量可行域;f1、f2分别为第1、2 阶段经典鲁棒优化目标函数;gj为两阶段经典鲁棒优化的约束条件。
1.3 单阶段分布鲁棒优化
经典鲁棒优化是不确定因素在一定范围内变化的条件下求解最优目标函数值,而分布鲁棒优化将经典鲁棒优化和随机优化相结合,是不确定因素的概率分布在一定范围内变化的条件下求解最优目标函数期望。单阶段分布鲁棒优化适用于在未知不确定参数的概率分布实现前进行决策的问题[7],与单阶段经典鲁棒优化相比,优势在于有效减弱了保守性,但鲁棒对等变换更复杂,一般而言计算负担更重,其表达式见式(3)。式中:P为不确定参数u的概率分布;ρ为概率分布簇;EP(f(x,u))为目标函数期望;sup 和inf 分别为取上确界函数和取下确界函数。
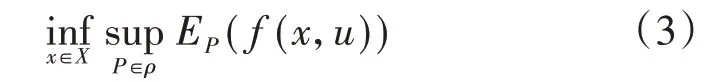
1.4 两阶段分布鲁棒优化
两阶段分布鲁棒优化模型适用于在不确定参数概率分布实现前、后2 个阶段分别确定部分决策变量的问题[7]。与两阶段经典鲁棒优化相比,两阶段分布鲁棒优化能显著降低决策保守性,但通常需要进行更复杂的鲁棒对等变换,导致更沉重的计算负担,其数学形式见式(4)。

1.5 鲁棒优化模型求解方法
在发输电系统优化规划中主要采用两阶段经典/分布鲁棒优化模型。这类模型通常是min-maxmin 3 层结构,求解思路为通过某些方式将中下层max-min 问题合并为max 子问题SP(SubProblem),与min 主问题进行主-子问题迭代求解。求解方法一般分为线性决策规则LDR(Linear Decision Rule)、Benders分解、列与约束生成C&CG(Column and Constraints Generation)三大类。LDR 构造两阶段决策变量与不确定变量的仿射关系式,将中下层问题合并为SP,适用于决策变量与不确定因素存在较强线性关系的问题,收敛速度快,但是对仿射关系的假设降低了解的最优性[8];Benders 分解基于对偶理论将中下层问题合并为SP,使用SP生成约束(对偶割)添加到主问题[9],其实质是约束生成算法,适用于变量较少而约束较多的问题,所得解的最优性优于LDR,但是通常迭代次数较多,求解速度相对较慢;C&CG基于KKT(Karush-Kuhn-Tucker)条件将中下层问题合并为SP,使用SP 生成约束(原始割)和变量(即列)添加到主问题,适用于变量较多而约束较少的问题,能以更少的迭代次数收敛到最优解[10]。此外,文献[11]综合应用Benders 分解与C&CG,在求解主问题的同时生成对偶割、原始割和变量,加速算法收敛;在某些发输电系统优化规划问题中,下层min问题含有0/1 决策变量,直接与中层max 问题合并无法保证解的最优性,为此,文献[12]提出了嵌套列与约束生成NC&CG(Nested Colunm and Constraints Gneration),对中下层max-min 问题使用C&CG,生成列与约束加入上层min 问题,较好地保证了解的最优性,但是也显著增加了迭代次数,求解速度较慢。
2 不确定集合构建方法
鲁棒优化问题通过不确定集合的方式对不确定参数建模,本文分别综述经典鲁棒优化和分布鲁棒优化的典型不确定集合类型及特点。
2.1 经典鲁棒优化的不确定集合
2.1.1 多面体不确定集合
由不确定参数波动区间构成的不确定集合称为多面体不确定集合(即盒式不确定集)[13],如式(5)所示。
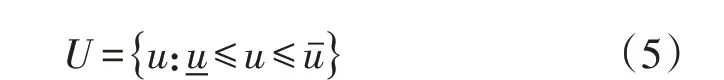
式中:uˉ、-u分别为不确定参数u的上、下界。多面体不确定集合形式简洁,便于鲁棒优化问题的对等变换,但对不确定性参数的刻画较粗糙,造成优化结果过于保守。
2.1.2 基数约束不确定集合
基数约束不确定集合在多面体不确定集合基础上对每个不确定参数偏差量进行约束,以更细致地刻画不确定参数的波动情况[13]。基数约束不确定集合在输电系统鲁棒优化中应用广泛、形式多样,其典型形式见式(6)。

式中:ui为第i个不确定参数;uˉi、-ui分别为ui的上、下界;ûi为第i个不确定参数平均值;Ω为所有不确定参数的集合;Γ为不确定集合的预算,用于约束不确定参数总偏差量。
2.1.3 椭球不确定集合
椭球不确定集合弥补了多面体/基数约束不确定集合无法刻画不确定变量相关性的缺陷,但是其鲁棒对等变换为二阶锥问题,应用于大规模问题的求解时计算量大[13],在发输电系统优化规划中应用较少,其典型形式见式(7)。

式中:u为不确定参数u组成的不确定向量;μ0和∑0分别为u的期望向量和协方差矩阵;γ为以μ0为中心的椭球不确定集合半径。
2.1.4 基于概率信息构建边界的不确定集合
文献[14]提出了基于概率信息构建边界的不确定集合。此类不确定集合基于概率信息合理地缩小多面体不确定集合范围,更加灵活,保守性更低,并且没有显著增加鲁棒对等变换复杂性,较易求解,其典型形式见式(8)[14]。


2.2 分布鲁棒优化的不确定集合
2.2.1 基于不确定参数矩信息的不确定集合
不确定参数的历史数据中包含丰富的矩信息(如一阶矩期望、二阶中心矩方差、三阶中心矩偏度等)。基于矩信息的不确定集合假定不确定参数的概率分布属于具有相同矩信息的一簇概率分布,可以分为矩信息确定的不确定集合和矩信息不确定的不确定集合。
1)矩信息确定的不确定集合。
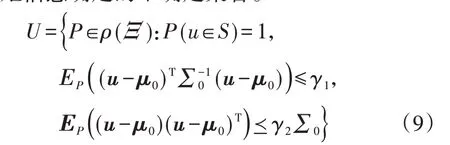
式中:Ξ为不确定参数u的支撑集合;S为不确定参数u的样本集合,S通常取为不确定参数u的多面体不确定集合;EP为期望向量;P∈ρ(Ξ)表示不确定参数u的概率分布函数P属于支撑集合Ξ上的概率分布簇;γ2为∑0的半定锥不确定集范围参数;-≺表示半定约束符号。由于具有相同矩信息的概率分布范围较大且相互之间存在较大差异,基于矩信息的不确定集合仍然会导致较保守的优化结果[15]。
2)矩信息不确定的不确定集合。

式中:μ和σ2分别为u的期望和方差;μˉ、-μ和-σ2、-σ2分别为期望和方差的上、下界。与矩信息确定的不确定集合相比,矩信息不确定更加适用于发输电系统优化规划中历史数据有限以及矩信息较不准确的场景,但也扩大了不确定集合的范围,导致结果更加保守[15]。
2.2.2 基于概率分布距离的不确定集合
基于概率分布距离的不确定集合假定不确定参数的真实概率分布属于某种参照概率分布(通常采用经验分布)附近范围内,其形式取决于选取的距离测度函数。典型的距离测度函数包括范数距离、KL(Kullback-Leibler)散度和Wasserstein距离。
1)基于范数距离的不确定集合。
基于范数距离的数学表示形式见式(11)。
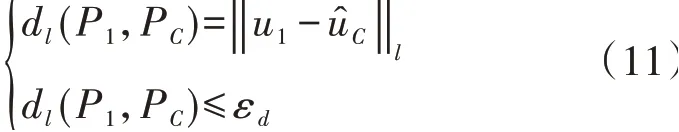
式中:P1、PC分别为不确定参数u1和参照随机变量ûC的概率分布;dl为P1、PC的范数距离;εd为dl的上限;l=1、2、∞分别对应于1-范数、2-范数以及无穷范数,其中1-范数和无穷范数因其线性性质便于鲁棒对等变换,在电力系统分布鲁棒优化中应用较多。但是1-范数和无穷范数衡量的是距离的绝对值,且会损失较多概率特征信息,造成距离测度的偏差[16]。
2)基于KL散度的不确定集合。
KL 散度起源于信息论,又称相对熵,形式见式(12)。

3)基于Wasserstein距离的不确定集合。

式中:∏(du1,du2)为不确定参数u1、u2的联合概率分布;Ξ2为所有可能的u1、u2联合概率分布构成的集合,在Ξ2中寻找某个联合分布使u1与ûC距离的期望最小,则此期望的下确界即为P1、PC的Wasserstein距离dW(P1,PC)。式(13)构建了以参照分布PC为中心、εW为半径的Wasserstein 球形不确定集合。相较于KL 散度,即便2 个分布的支撑集没有重叠,Wasserstein 距离仍然能刻画分布间的距离,且当历史数据足够多时,一定能够保证算法的收敛性[17]。但是基于Wasserstein球形不确定集合的鲁棒优化计算复杂性较高,通常需要开发估计算法才能够高效求解。
3 鲁棒优化在发输电系统优化规划的应用
3.1 考虑节点注入功率不确定性
对节点注入功率不确定性的研究主要集中在风电和负荷。现有文献从多种角度考虑了风电、负荷的不确定性,这些模型从考虑不确定变量的概率分布特征上可分为基于经典鲁棒优化和基于分布鲁棒优化的模型。
3.1.1 基于经典鲁棒优化的模型
文献[18-19]率先在机组组合与输电网规划问题中引入多面体集合表示风电和负荷的不确定性,为后续研究奠定了基础。为减少鲁棒优化的保守性,文献[20-21]采用加权的方式将鲁棒优化和随机优化相结合,建立了随机鲁棒机组组合模型。文献[22]提出了风电出力区间不确定性的区间鲁棒不确定集合。文献[11]以弃风与切负荷风险最小为鲁棒优化目标函数,较好地协调了经济性与安全性。为提高两阶段鲁棒优化的求解效率,文献[23]只搜索w座风电场出力范围构成的多面体顶点(文中定义为风电极限场景)。文献[8]利用线性决策规则,假定发电出力是风电和负荷的仿射函数,避免了通过割平面算法引入大量额外约束。文献[24]建立了输储联合鲁棒规划模型,由于储能投建在第2 阶段决策,提出了NC&CG 算法加以求解。文献[25]建立了多阶段鲁棒机组组合模型,并基于Benders分解思想设计了相应算法进行求解。
在考虑不确定节点注入功率相关性方面,现有研究思路有3 种:①将考虑相关性的场景与鲁棒优化相结合;②基于统计参数构建刻画相关性的不确定集合;③由数据驱动,构建含相关性的不确定集合。针对思路①,文献[26]利用Taguchi正交数组测试抽取典型风电相关出力场景。文献[27]提出启发式矩匹配方法抽取风电相关场景并与文献[28]的方法进行了对比。文献[29]提出了考虑多场景概率的多面体不确定集合提取风电相关场景。文献[30-31]则分四季聚类构建风电负荷相关场景。针对思路②,文献[32]提出了多带宽多面体集合,刻画负荷波动范围的时空相关性。文献[33]基于时序自相关系数构建多面体不确定集以反映风电时间相关性。文献[34]考虑了单时段各风电场的总波动不确定性和各时段单风电场波动不确定性,共同构成了刻画风电场时空相关性的不确定集合。文献[35]构建了含风电负荷协方差矩阵信息的椭球不确定集合以考虑风电负荷的时空相关性。思路③通常基于数据挖掘或统计分析方法构建更符合实际的不确定集合。由于不确定变量的相关性体现在历史数据中,而这类不确定集合的边界正是由历史数据驱动生成,所以这类不确定集合大量削减了传统不确定集合中实际不存在的场景,有效降低了保守性。文献[36]利用狄利克雷过程混合模型DPMM(Dirichlet Process Mixture Model)构建了数据驱动的风电出力多面体不确定集合,并与传统多面体不确定集合进行了对比,保守性显著降低。文献[37]运用高维闭包椭球算法,构建了基于风电出力历史数据的高维椭球不确定集合。文献[38]基于历史数据构造一系列超平面,组合成基于超平面的不确定集合HPUS(HyperPlane based Uncertainty Set),结合了盒式不确定集合易于求解和凸包不确定集合保守性较弱的优点,在减轻计算负担和减弱保守性间达到了较好的平衡。上述文献已从风电和负荷的时间、空间、时空相关性3个角度展开研究,建模思路主要基于聚类、统计参数(如时间序列自相关系数、协方差矩阵)和数据驱动3 类,后续可将3 类思路结合,基于典型聚类场景下的相关性挖掘方法构建不确定集合,更细致刻画节点注入功率的时空相关性。
总体而言,考虑节点注入功率不确定性的发输电系统经典鲁棒优化规划大多为两阶段优化模型,其具有较高的求解效率且不存在收敛性问题。为了减弱模型保守性,可以松弛目标函数(例如以风险最小为目标),或者构建更合理的不确定集合(例如考虑相关性的不确定集合,注入功率变化范围可变的不确定集合)。但是,由于此类模型未充分考虑最恶劣节点注入功率场景发生的概率,也未充分挖掘节点注入功率的历史信息,模型保守性存在较大的减少空间。
3.1.2 基于分布鲁棒优化的模型
按节点注入功率的矩信息是否有不确定性,可以分为2 类:①从历史数据得出确定的矩信息,构建以式(9)为代表的不确定集合;②构建刻画矩信息自身不确定性的不确定集合。对于类型①,文献[39-42]构建了风电出力期望和协方差椭球不确定集合,转化为半定规划求解。文献[43]在文献[39-42]的不确定集合基础上,增加了风电出力α-双峰性不确定集合,仍然转化为半定规划求解。对于类型②,文献[44-45]考虑了风电期望波动范围的不确定性。文献[46]考虑了风电期望和方差预测误差的不确定性。文献[47]构建了考虑风电期望、方差以及协方差约束的不确定集合。文献[48]不仅约束了期望方差范围,还约束了净负荷在各时间段内总波动方差的范围,以反映风电负荷的时间相关性。从数学本质上看,基于矩信息的不确定集合是经典鲁棒优化不确定集合的松弛,一定程度上减弱了经典鲁棒优化的保守性,但是仍然面临2 个方面问题:①方差、协方差信息的引入导致分布鲁棒模型呈现非线性,需要经过复杂的数学变换,将其转化为半定规划进行求解,在大规模系统中计算负担沉重;②拥有相同矩信息的概率分布范围十分广泛,从不确定参数的历史数据中挖掘更多的概率信息可以进一步降低模型保守程度。
在基于节点注入功率的概率分布距离信息的分布鲁棒模型方面,文献[49-52]均运用无穷范数与1-范数衡量风电出力实际概率分布与经验概率分布的距离,由于上述2 种范数具有线性性质,可转化为混合整数线性规划求解。文献[53]基于KL 散度构建了混合整数非线性机组组合模型,用广义Benders分解求解。文献[54-56]应用Wasserstein 距离刻画风电出力实际与经验概率分布的距离。在求解方面,现有文献均基于以下引理[47]:对属于支撑集合Ξ的变量u,以样本集{û1,û2,…,ûZ}构建Wasserstein距离,如果损失函数Φ(u)上半连续,则最差的损失函数期望见式(14)。

式中:λ为拉格朗日对偶乘子;εr为锐化因子;τf为辅助变量。约束条件中的范数可取1-范数、2-范数或无穷范数,由研究人员按需设定。由于该引理引入的约束条件数量与样本数量成正比,计算量较大,文献[54-56]利用发输电系统优化规划问题的凸性,提出了不同的上估计方法对式(14)进行近似求解。文献[55-59]构建了同时含风电出力矩信息和概率分布距离信息的不确定集合,进一步协调了模型的安全性与经济性。与基于矩信息相比,基于距离信息的不确定集合需在高置信度下成立,将实际概率分布约束在以参照概率分布为中心的小范围内,更充分地利用节点注入功率的历史信息减弱了模型保守性,但求解复杂性相对较高,而且部分模型无法保证收敛。后续可研究更合理的距离信息不确定集线性化方法,同时嵌入具有线性性质的矩信息不确定集,构建含有丰富概率信息的混合整数线性发输电系统鲁棒优化规划模型,更好地平衡了不确定集的保守性和算法的复杂性。
3.2 考虑电源容量增长及成本不确定性
电源的容量、位置、建设周期、退役时间以及投资运行成本等是电源不确定性的主要来源。现有文献从不同角度研究了电源不确定性对发输电系统鲁棒优化规划的影响。
3.2.1 两阶段经典鲁棒优化
文献[60-62]基于基数不确定集合建立了考虑电源容量增长不确定性的两阶段鲁棒优化规划模型,其中文献[60]考虑了电源投资成本和发电成本不确定性,文献[61-62]考虑电源容量增长不确定性。文献[47]对比分析了以最小悔值和以最小成本为目标的输电网鲁棒规划。这些模型形式较简洁,求解相对简便,为结合随机与鲁棒的模型和多阶段鲁棒模型奠定了基础。文献[63-64]将电源投建退役视为长期不确定性,用基数不确定集合刻画,将可再生能源的出力和负荷波动视为短期不确定性,用随机场景方式刻画,建立了随机与鲁棒相结合的优化模型。其中文献[63]以电源容量为长期不确定性,在不同负荷场景中设置不同的发电出力分配因子。文献[64]以发电成本为长期不确定性,利用K-means聚类形成多个发电与负荷相关场景,建立了发输电系统随机鲁棒规划模型。
3.2.2 多阶段经典鲁棒优化
文献[65]利用多阶段鲁棒不确定集合刻画了电源逐年建设、退役的不确定性,并与逐年规划的结果进行了对比,逐年电源建设不确定性集合如式(15)所示。

总体而言,考虑电源容量增长以及成本不确定性的发输电系统鲁棒优化规划均基于经典鲁棒优化模型,并且已经发展到了多阶段,更加符合电源逐年投建、退役的现实场景,但是解空间也显著扩大。现有研究仍然基于C&CG 算法进行求解,在模型扩展为大规模、多时段问题时计算负担沉重。如何生成割约束,如何利用模型结构特性巧妙剪枝,使模型适用于实际大规模发输电系统,是值得深入研究的问题。
3.3 考虑输电网络状态不确定性
输电网络状态不确定性的主要来源是元件老化故障、偶发自然灾害(雷击、山火、雪灾、台风等)以及人为恶意攻击。在发输电系统优化规划问题中,为了刻画输电线路N-k故障,通常需要引入CkN种故障场景,计算量巨大。而发输电系统鲁棒优化规划方法为考虑输电网络状态不确定性提供了不同思路。
3.3.1 基于经典鲁棒优化
文献[67]率先用两阶段鲁棒优化解决N-k故障约束的机组组合问题,其构建的元件N-k故障不确定集合见式(16)。

式中:L、G分别为所有线路、所有发电机集合;nl、ng分别为线路、发电机总数;k为预设的故障元件数量上限。模型迭代寻找最严重的N-k故障并优化相应的开机组合,直至最严重的N-k故障都无法造成功率不平衡为止。文献[68-69]将此类型N-k故障集合应用到了输电网鲁棒规划问题。文献[70]将此类型N-k故障集合拓展为了多阶段形式,以刻画台风在不同时间段对输电线路的破坏情况。基于鲁棒优化考虑输电网络状态不确定性的实质是枚举了部分故障场景(即只寻找最严重的故障情形)并进行相应的优化规划,显著减轻了N-k故障约束的计算负担,使得发输电系统优化规划模型中更细致地考虑N-k故障成为可能。
3.3.2 基于分布鲁棒优化
文献[71]提出了考虑故障概率矩信息的分布鲁棒机组组合模型,其中N-k故障的分布鲁棒不确定集合见式(17)。
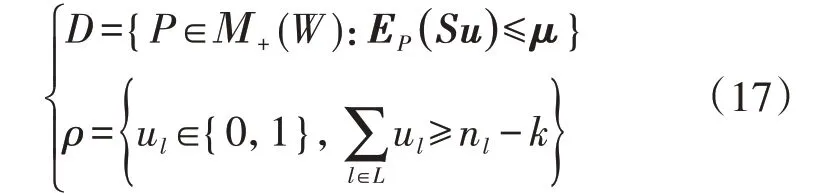
式中:D为N-k故障的概率分布组成的模糊集合;W为线路状态变量u的集合,需要满足线路N-k约束;Μ+(W)为由W中线路状态变量ul的概率分布组成的集合,即线路状态变量ul的支撑集合;μ为线路故障的统计期望值(一阶矩)向量;S为预先定义的系数矩阵;EP(Su)≤μ刻画了特定故障情形的期望应在线路故障的统计期望值范围内。在此故障集合下的机组组合问题就是寻找最恶劣的线路N-k故障概率分布,并最小化相应的机组启停和运行成本期望。文献[72]提出了考虑故障概率分布距离的分布鲁棒输电网强化模型,其N-k线路故障分布鲁棒不确定集合见式(18)。

4 展望
4.1 同时考虑概率分布与时空相关性
优化结果偏向保守是鲁棒优化的固有局限,模型变换复杂和计算负担沉重则是分布鲁棒优化的主要问题。对发输电系统鲁棒优化规划而言,保守性主要来源于2 个方面:①仅利用了历史数据所反映的不确定参数波动范围而未考虑概率信息;②忽略了不确定因素时空相关性,导致不确定集合包含大量现实中不存在的场景。虽然不乏文献分别从考虑时空相关性、考虑概率分布信息角度减弱鲁棒优化的保守性,但是这些模型通常鲁棒对等变换较为复杂,在大规模系统中应用困难。例如:矩不确定集合可以通过协方差刻画相关性,但也导致鲁棒对等变换是二阶锥规划/半定规划[5];基于Wasserstein 距离的分布鲁棒优化,其对等变换问题规模太大,必须使用估计算法近似计算[17]。由于分别考虑相关性和概率信息已使模型较为复杂,鲜有文献同时考虑概率信息与相关性。
因此,有必要用简洁易解的方式同时考虑不确定参数的相关性与概率信息,有效协调发输电系统优化规划模型保守性、准确性和求解效率,从数学角度出发,这要求鲁棒模型与对等变换尽量保持混合整数线性性质,并且需要避免使用假设或者估计算法。从可行性出发,综合应用聚类分析和线性统计参数(如一阶矩)构建节点注入功率不确定集合,即可在混合整数线性规划前提下,计及多种运行方式下节点注入功率的时空相关性和概率信息,如式(19)、(20)所示。

式中:ps为第s种场景的概率,总共聚类得到Ns种场景;us为第s种场景下的不确定变量;u0s为第s种场景下不确定变量的均值;γ1s、γ2s分别为每种场景下,不确定变量与平均值的偏差控制参数。所提模型将不确定场景聚类,再构建各典型场景的均值偏差期望不确定集合,即可在混合整数线性规划前提下,计及多种场景下的不确定变量相关性和概率信息,以此协调保守性、准确性和求解效率。
4.2 深入考虑安全稳定约束
现有发输电系统鲁棒优化规划通过多种方式考虑了元件N-k约束,所得优化方案可以保障系统静态安全,但可能无法满足其他安全稳定要求。后校验方法能够判断优化方案是否达到安全稳定标准,但存在2 点问题:①即便经过反复迭代,所得方案仍可能无法通过安全稳定校验;②即便优化方案通过了安全稳定校验,也可能不是满足相应安全稳定约束的最优方案。因此,如何在发输电系统鲁棒优化规划中深入考虑更多安全稳定约束,值得深入研究。对于可行性,暂态功角稳定、频率稳定、短路电流等安全稳定要求均可以与鲁棒优化模型结合。例如:通过暂态稳定SP 生成线性的暂态稳定割反馈给鲁棒优化主问题进行主-子问题迭代,即可在不显著增加模型复杂性的前提下,将暂态稳定约束嵌入发输电系统鲁棒优化规划模型。具体而言,鲁棒优化主问题生成暂态稳定SP 的边界条件(例如初步规划/调度方案),暂态稳定SP 的计算过程如下:通过时域仿真寻找故障失步机群,基于扩展等面积准则绘制失步机群等效加速曲线,再应用轨迹灵敏度分析,构建发电出力调整量与稳定裕度的线性关系表达式[72],作为约束加入主问题,并扩展鲁棒优化SP 的对偶目标函数和约束,进行主-子问题迭代求解。考虑暂态稳定约束的发输电系统鲁棒优化规划模型见式(21)。

式中:ε为暂态稳定裕度目标值,根据工程需求设定;η为暂态稳定裕度。
4.3 基于鲁棒优化的弹性发输电系统优化规划
近年来,电力系统遭受自然灾害或人为攻击的频率明显上升,弹性电网成为研究热点。“弹性”要求电力系统遭受小概率、高损失极端事件(通常分为自然灾害与人为攻击2 类)时具有恢复力[74],而鲁棒优化的目标是寻找不确定因素极端实现场景下的最佳决策,正适合应用于弹性电网优化规划问题。基于鲁棒优化的弹性发输电系统优化规划一般为“防御-攻击-防御”两阶段模型,第1 阶段在极端事件前进行预防性决策,第2 阶段在极端事件发生中、发生后进行实时及事后恢复性决策,其中不确定集合是刻画极端事件的关键。在自然灾害方面,可从3 个角度构建鲁棒不确定集合:①刻画自然灾害时空演变特性,例如通过多阶段、故障范围变化的不确定集合刻画台风移动对电网的破坏[75];②刻画自然灾害下元件故障概率不确定性,例如基于元件在洪水下的故障概率曲线以及洪水强度和频率历史变化范围,构建元件故障概率不确定性的不确定集合[76];③综合考虑灾害时空特性及元件概率不确定性[77-78]。在人为攻击方面,物理信息系统协同攻击作为一种新型的小概率、高损失极端场景受到广受关注。攻击者通过开断刀闸等方式破坏网架结构,同时向信息系统注入虚假数据掩盖物理攻击,躲避调度中心的故障监测,造成负荷损失甚至系统崩溃。已有文献基于两阶段经典鲁棒优化对此类攻击进行建模和抵御,还未计及物理信息攻击的概率问题[79-81]。后续可基于分布鲁棒优化对考虑物理信息协同攻击概率的弹性发输电系统优化规划展开研究。角度有二:①攻击者完整掌握电网拓扑的情况下,攻击者可从多种角度对元件重要性、脆弱性进行评估,侧重攻击重要/脆弱元件,由此可构建考虑元件被攻击概率的分布鲁棒不确定集合;②攻击者对不同区域电网拓扑结构掌握程度不同的情况下,攻击者对各区域的攻击意愿以及各区域元件重要性评估存在差异,可构建刻画区域以及元件被攻击概率不确定性的分布鲁棒不确定集合,并通过调度/规划措施进行抵御和恢复。
5 结论
本文对发输电系统鲁棒优化规划研究进行了综述和展望。从数学角度出发,现有发输电系统鲁棒优化规划模型可以分为经典鲁棒优化和分布鲁棒优化两大类,每一大类可分为单阶段、两阶段两小类,其中经典鲁棒优化主要采用多面体和基数约束不确定集合,分布鲁棒优化多采用矩信息或距离信息不确定集合。从研究物理问题角度出发,现有发输电系统鲁棒优化规划模型可分为考虑节点注入功率不确定性、考虑电源容量增长及成本不确定性、考虑输电网络状态不确定性这3 类。考虑节点注入功率不确定性的研究最丰富,后续可以考虑用简洁易解的方式同时计及节点注入功率的相关性与概率信息;考虑电源容量增长以及成本不确定性的模型已从单阶段发展到多阶段,如何高效求解随之成为挑战;考虑网络状态不确定性的研究可以分为不考虑和考虑故障概率信息这2 类,后续研究方向可以考虑更多安全稳定约束,或基于鲁棒优化进行弹性发输电系统优化规划。

