非隔离并网逆变器进网电流直流分量抑制策略参数优化设计

王 鹏，李明明，肖华锋，2

（1. 东南大学电气工程学院，江苏 南京 210096；2. 江苏省智能电网技术与装备重点实验室，江苏 南京 210096）

0 引言

非隔离并网逆变器（TLI）具有效率高、体积小、成本低等特性，因此在分布式光伏并网系统中被大量应用。但由于取消了连接至公共连接点（PCC）的工频变压器，进而失去了“变压器隔直”这一屏障，TLI 进网电流中可能含有直流分量。该直流分量将引起一系列危害，如PCC上级变压器饱和、加快电缆的腐蚀以及影响计量表计量的准确性等。

为促进TLI 应用和保证各电气设备安全可靠运行，各国标准对进网电流中的直流分量均提出了严格的指标限制，IEC62109-2 与GB／T 37408—2019分别要求进网电流中的直流分量小于额定输出电流的1%和0.5%［1］。

经分析，引起直流分量的原因包含功率器件特性差异、门极驱动电路不对称、电流传感器的测量误差以及信号调理电路和模数转换装置引入的直流偏差等［2］。为了防止上述因素引起进网电流直流分量超过标准规定的限值，一些有效的抑制措施被相继提出，其大致可以分为检测反馈法、智能算法和电容隔直法这3类［3-5］。检测反馈法需要额外的检测电路或者较为复杂的运算方法来提取较大幅值的基波电流中占比较少的直流分量。智能算法是一种采用高级算法进行直流分量提取和抑制的策略，具有鲁棒性强的特点，但需要消耗较多的计算资源，算法的实时性也有待提高。电容隔直法利用电容器“隔直通交”固有特性，根据电容器的位置，可以分为直流侧电容隔直法和交流侧电容隔直法。半桥类拓扑是典型的直流侧电容隔直法拓扑结构，具有直流分量抑制能力，但也存在电容电压不平衡和直流电压利用率较低等不足［6］。交流侧电容隔直法简单直观，被应用于各类无直流分量抑制能力的逆变器，但也存在电容值选取困难［7］、电容的串联电阻会降低逆变器效率等不足。

为此，有学者提出利用虚拟电容抑制进网电流中的直流分量［8-14］，在控制器中引入基于进网电流积分运算的前馈项来等价实现交流侧串联电容的直流分量抑制效果，但虚拟电容法存在影响原本电流控制器的稳定性及其动态响应等问题。因此采用虚拟电容法通常要对电流控制器参数和虚拟电容值进行合理整定，才能满足直流分量抑制速度快并且基波电流响应又快又准的要求。文献［10］对比了不同虚拟电容值下系统的单位阶跃响应，定性地选出虚拟电容值，但没有具体分析虚拟电容值对基波电流响应的影响。文献［11］借助根轨迹和Bode 图等频域分析工具，综合分析了虚拟电容与比例谐振（PR）控制器的相互影响，但最终选取的参数值是由仿真尝试后得出的经验值，并不能形成一般的指导原则。文献［12-13］将虚拟电容的概念应用于三相并网逆变器系统，使用根轨迹法分析了比例积分谐振（PIR）控制器的参数选择，但论文中认为工程上对直流分量抑制的动态性能要求不高，直接选取较大的虚拟电容值，所采用的处理方式过于简单。此外，以上文献在选取虚拟电容值和电流控制器参数时均未对系统的时域指标进行约束。虽然文献［14］从稳态误差、开环系统基波幅值增益、幅值裕度和相位裕度角等方面对控制器参数设计提出了具体要求，并通过拟合约束条件曲线得到了参数选择的允许域，但步骤过于繁琐。

为了对电流控制器参数和虚拟电容值进行合理的整定，本文提出一种基于PR 和虚拟电容（PR+C）控制器的TLI 参数优化方法，旨在兼顾直流分量抑制速度和基波电流跟踪效果，并通过实验验证了参数选择的合理性。提出的评价指标易于实现，可以指导TLI实际调试时控制器参数整定工作。

1 含虚拟电容的TLI控制系统

图1 为含虚拟电容的TLI 控制框图。图中，K为TLI 工作在高频时的等效增益；C为虚拟电容值，其影响直流分量的抑制效果；iref为电流参考值；G（s）为电流控制器传递函数；uin为桥臂电压；ug为电网电压；ig为TLI 进网电流；L为滤波器电感；R为滤波器电阻。

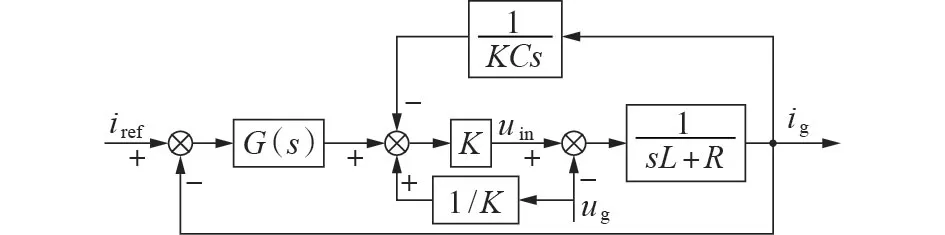
图1 含虚拟电容的TLI控制框图Fig.1 Control block diagram of TLI with virtual capacitor

由于电网电压的前馈控制作用，电网电压对系统的影响可以基本忽略，控制系统变为单输入单输出系统。

2 虚拟电容与PR控制器的相互影响分析

为了阐明虚拟电容与PR控制器的相互影响，需要借助时域响应和频域响应曲线做进一步分析。TLI 的基本参数设置为：K=360；ω=100π rad／s；R=0.24 Ω；L=0.0022 H。

2.1 虚拟电容对直流分量抑制能力分析

在式（2）中，令s=jω=0，则有ig(jω)=0。即理论上，虚拟电容抑制直流分量的稳态误差为0。但电容值选取不同，直流分量抑制速度和响应形式不同。

当kP=0.05、kR=10 时，在第0 s 输入阶跃信号，电流参考值由0 突变为1 A，不同虚拟电容值下TLI 系统的阶跃响应曲线如图2所示。

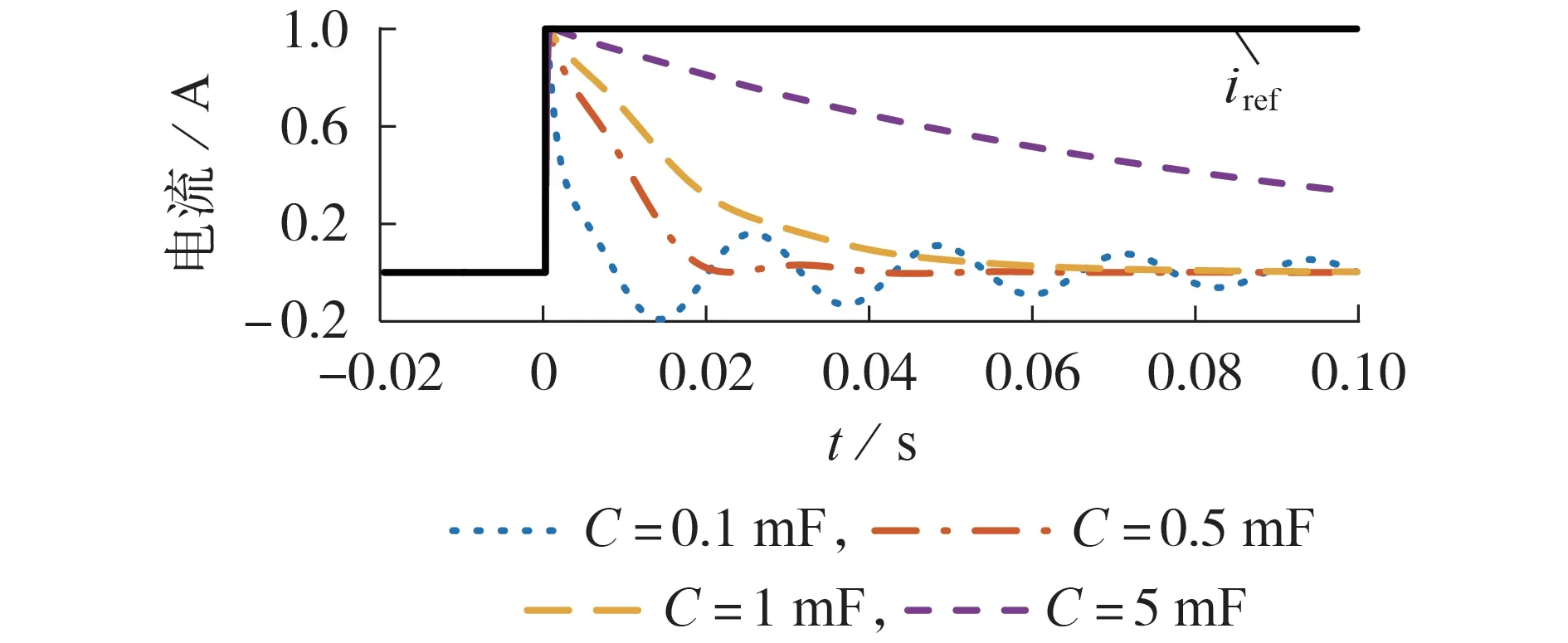
图2 不同虚拟电容值下TLI系统的阶跃响应Fig.2 Step response of TLI system with different virtual capacitor values

观察4 种虚拟电容值下的阶跃响应可以得出以下结论：①虚拟电容值过大会导致直流分量抑制的动态响应变慢；②虚拟电容值过小会导致系统输出电流振荡；③虚拟电容值大小不影响系统阶跃响应的稳态值（时间趋于无穷）。

上述结论可以通过绘制TLI 系统闭环传递函数的频域响应曲线进行验证。当系统无虚拟电容以及虚拟电容值分别取0.1、0.5、1、5 mF 时TLI 系统的频域响应曲线如图3 所示。由图可知，无虚拟电容时，系统在低频（趋近于0）处的幅值增益为0，而当C从5 mF 减小至0.1 mF 时，系统对低频成分的衰减逐渐增大。同时也可发现，在50 Hz附近，电容越小，系统的幅值增益越大，因此当输入信号含有频率为50 Hz的电流分量时易引起系统振荡。

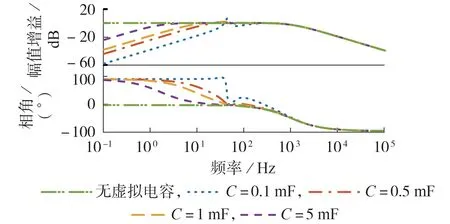
图3 不同虚拟电容值下TLI系统的频域响应曲线Fig.3 Frequency-domain response curves of TLI system with different virtual capacitor values

综上所述，为了加速直流分量抑制速度并减小系统振荡幅度，在选取虚拟电容值时应考虑一定的约束条件，将在下文中进行介绍。

2.2 虚拟电容对基波电流跟踪效果的影响分析

2.2.1 稳态特性

令s=j100 π，化简式（2）可得ig(jω)/iref(jω)=1。这说明由于PR控制器的作用，加入虚拟电容前、后，系统在频率为50 Hz 处所对应的输入电流信号幅值增益均为0。故理论上加入虚拟电容不会影响TLI系统输入电流的稳态特性。

2.2.2 动态特性

为了分析虚拟电容对基波电流的动态跟踪效果，在不同虚拟电容值下绘制进网电流参考突变时的电流响应曲线，如图4 所示。其中电流参考值在0.265 s 时由10 A 骤降为5 A，PR 控制器参数kP=0.05，kR=10，C分别取0.1、0.5、1、5 mF。可以看出，当虚拟电容值为0.1 mF 时，进网电流相比参考电流产生了明显的偏移，且在2 个周期后仍不能跟踪参考电流，而其余虚拟电容值下进网电流的跟踪效果较好。这是因为虚拟电容值越小，频带越窄，动态响应速度越慢。故虚拟电容值越大，对进网电流控制效果越差。

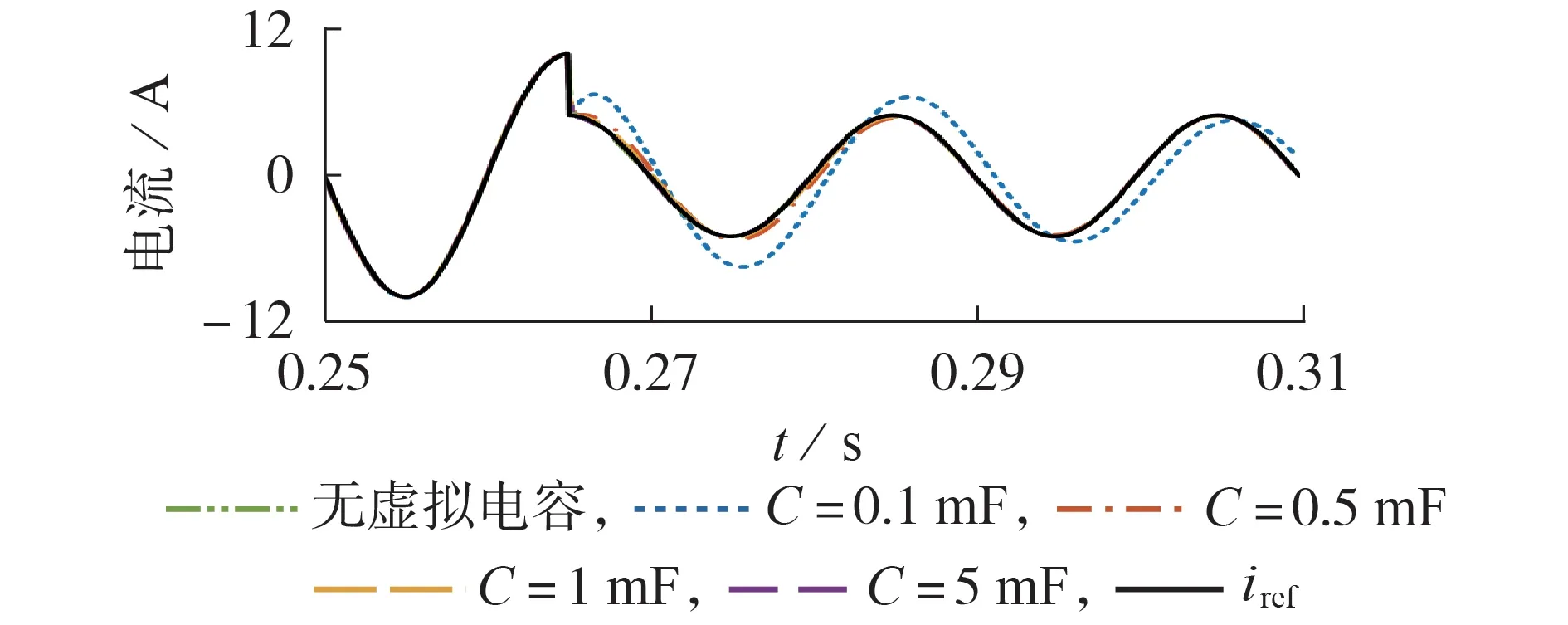
图4 不同虚拟电容值下TLI系统动态响应特性Fig.4 Dynamic response characteristics of TLI system with different virtual capacitor values

2.3 PR控制器对直流分量抑制能力的影响分析

为了说明PR 控制器参数对直流分量抑制能力的影响，设虚拟电容值C=1 mF，对比不同的PR 控制器参数下TLI 系统的阶跃响应。①当kR=10，kP分别为0、0.01、0.03 和0.05 时，TLI 系统的阶跃响应曲线见图5 上图；②当kP=0.05，kR分别为0、3、6 和10 时，TLI 系统的阶跃响应曲线见图5 下图。由图可知，kP取值的不同对TLI 系统阶跃响应的影响较大。当kP逐渐增大时，阶跃响应的振荡逐渐消除，直流分量的抑制速度也会逐渐减慢。相较而言，kR取值的不同对TLI系统阶跃响应的影响较小。

图5 不同PR控制器参数下TLI系统阶跃响应曲线Fig.5 Step response curves of TLI system with different parameters of PR controller

综上，虚拟电容与PR 控制器相互耦合，共同影响TLI 系统的基波电流跟踪性能和直流分量抑制能力。因此，有必要对参数选择的结果进行量化，并建立约束条件，以优化TLI系统的运行性能。

3 参数优化设计

3.1 约束条件建立

3.1.1 频域约束

本节针对控制系统的频域响应提出评价指标，以判断系统运行的稳定性。设TLI 开环系统的幅值裕度不低于6 dB、相位裕度在［30°，90°］范围内［15］。由以上2 个裕度条件可以在参数空间求出一个区域，以便下文求解参数最优解。根据图1 可得控制系统的开环传递函数为：

式中：D(s)=CLs4+CRs3+(CLω2+1)s2+CRω2s+ω2。

由于本文采用理想PR控制器，幅值裕度趋向于无穷大，满足幅值裕度约束［16］。在已知TLI 系统的其他基本参数后可得频域指标kP、kR、C满足：

式中：MP为相位裕度；ωc为最大的开环截止频率。根据式（5）可以确定关于kP、kR、C的参数选择区域。

3.1.2 时域约束

频域约束不能判断系统时域特征的优劣，本节针对系统的时域响应提出评价指标，以判断控制系统直流分量的抑制效果和基波电流的跟踪效果。

根据2.3 节分析，由于控制参数不同，阶跃响应的形式可以分为振荡衰减和非振荡2 种响应形式。无论哪种形式均能达到期望的响应性能，本文重点讨论振荡衰减响应形式。当系统的阶跃响应形式为振荡衰减时，采用如下3种指标进行评价。

1）设衰减比n为：

式中：hmax、hmin分别为系统的阶跃响应振荡幅值的最大、最小值。当n越小时，振荡幅度越大，直流分量抑制效果越好。

2）设tnp为系统振荡收敛时间，满足：

式中：R（t）为给定的输入信号响应；C（t）为系统响应；ε（t-0.105）为延时至0.105 s的单位阶跃函数；T=0.02 s。S越小，基波电流的跟踪越误差越小，PR 控制器的控制效果越好。

综合以上3点，可得评价TLI系统交直流控制性能的目标函数［17］为：

式中：α、β、γ分别为3种指标的权重，采用CRITIC 客观赋权法选定指标权重值，分别取α=0.41、β=0.39、γ=0.20［18］。

3.2 参数优化求解

本节进行参数优化的求解，TLI 参数同第2 节设置。首先采用有限离散化数值运算的方式，求出控制参数不同时系统的相位裕度。考虑计算机算力和实际系统的带宽限制，此处控制参数kP的计算步长为0.001，取值范围为（0，0.05］；控制参数kR的计算步长为1，取值范围为（0，20］；C的计算步长为0.1 mF，取值范围为（0，5］mF。

相位裕度计算结果如附录A 图A1 所示，该三维图中每个点都对应一个参数组（kP，kR，C）。图中左侧区域点的相位裕度小于30°，采用灰色空心圆进行标记；右侧区域为满足相位裕度的点，此处按颜色区分不同参数下系统的相位裕度。

接着求解使目标函数最小的参数组。由于不同待定参数下的约束指标数值相差很大，甚至不在一个数量级，需要对各组控制参数下的同一指标值进行归一化处理，使原本的数据归一化至区间［0，1］上，如式（10）所示。

式中：A(kP，kR，C)为各组kP、kR、C下的指标函数值；Amax(kP，kR，C)、Amin(kP，kR，C)分别为所有kP、kR、C取值下指标函数值的最大、最小值；A͂(kP，kR，C)为归一化后的指标函数值。

依此类推，对所有的指标进行上述归一化处理后，再对各个指标的进行加权计算目标函数值。令α=0.41、β=0.39、γ=0.20，筛选附录A 图A1 中满足阶跃响应为衰减振荡形式的参数组，代入式（9）计算目标函数值。此处同样以颜色区分数值大小，计算结果如附录A图A2所示。最终，将各参数组下的目标函数值从小到大排列，可得F的最小值为0.045 925。此时最优控制参数为kP=0.036，kR=8，C=0.7 mF。

4 实验验证

为了验证上述参数优化方法的有效性以及虚拟电容的可行性，搭建了基于TMS320F28335主控DSP的单相TLI 实验平台。其主电路采用Heric 拓扑，输出端接入对称双滤波电感，实验参数见附录A 表A1。将实验参数输入参数优化程序，计算得到的最优控制参数与3.2节分析结果相一致。

对于真实的TLI 系统，由于采样延迟、信号处理延迟、TLI 开关延迟和随机噪声等因素，系统的带宽不能无限制被提高［19］。而系统带宽主要由kP决定，当kP较大时对高频噪声的抑制能力就会减弱。因此在选择控制参数组时要对优化结果进行实验校核，排除使系统发生高频振荡的参数组。

首先，设控制参数kP=0.036、kR=8，在DSP中编写相应的控制程序，使虚拟电容值为0.7 mF，此时所得实验结果如下。

首先TLI经历软启动后保持电流幅值为10 A 运行，然后第0.235 s 时设置幅值突变点，电流幅值突变为5 A，最后在第0.41 s 时，由负向正过零点处给参考电流叠加幅值为1 A 的直流分量，则参考电流变为5 sin（ωt+π）+1。图6（a）、（b）分别为幅值突变点和直流分量注入点前后系统动态响应过程波形。可以看到，在该控制参数下基波电流跟踪性能效果良好，直流分量可在2个周期后被迅速抑制。

图6 TLI系统动态响应过程波形Fig.6 Waveforms of dynamic response process of TLI system

此外，为了验证优化参数的合理性，选取3 组不同的控制参数进行对比，对比结果见表1。设第1组中α=100%，所得控制参数能够较好地抑制直流分量；设第2 组中γ=100%，所得控制参数能够较好地跟踪基波电流；第3 组为使目标函数F较大时的控制参数，由表可知，基波电流跟踪性能及直流分量抑制效果较差；第4 组为本文设计的控制参数，该参数下基波电流跟踪性能及直流分量抑制效果最好。

表1 不同控制参数下基波电流跟踪性能及直流分量抑制效果Table 1 Fundamental current tracking performance and DC component suppression effect under different control parameters

将进网电流波形导入示波器，并在MATLAB 中进行数据分析，对表1 所示结果进行定量分析，最终得到各组各项指标如表2 所示，表中T=0.02 s 为电网周期。在基波电流跟踪性能方面，设平均绝对误差和调节时间为评价标准：平均绝对误差为电流幅值突变后2 个周期内所有数据点与参考电流偏差取绝对值后的平均值；调节时间的计算方式为独立计算每个电网周期内的平均绝对误差，当该误差减小到5 A 的5%以下时所消耗的电网周期数。在直流分量抑制效果方面，采用滑动窗口平均法［20］，提取进网电流中的直流分量，设直流分量衰减比和调节时间为评价标准：直流分量衰减比为直流分量注入后进网电流直流分量波形中第1 个波谷与波峰的比值；调节时间为直流分量被抑制到1 A 的5%内时所消耗的时间。由表2 可知，本文设计的控制参数下基波电流跟踪性能和直流分量抑制效果较好。

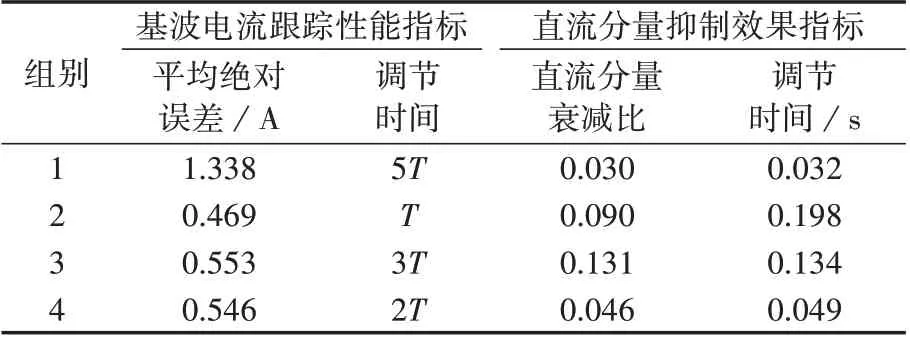
表2 不同控制参数下基波电流跟踪性能及直流分量抑制效果评价指标Table 2 Evaluating indicators of fundamental current tracking performance and DC component suppression effect under different control parameters

5 结论

在抑制TLI 进网电流直流分量的虚拟电容法中，电容参数和PR 控制器参数相互耦合，共同影响TLI系统的基波电流跟踪性能和直流分量抑制能力。本文提出一种PR+C 控制器参数优化方法，通过数值计算得出最优参数组；通过调节目标函数的权重，按需平衡TLI 进网电流直流分量的抑制速度和基波电流跟踪效果。对比实验表明所提方法具有良好的基波电流跟踪性能及直流分量抑制能力；经数据分析，采用所设计的参数在基波电流跟踪性能及直流分量抑制效果的评价指标方面均具有显著优势。从定性和定量的角度证实了本文所提参数优化方法的可行性。

附录见本刊网络版（http：//www.epae.cn）。