综合模型聚合和参数辨识的风电场多机等值及参数整体辨识

潘学萍，戚相威，梁 伟，雍成立，丁新虎，李 威，朱 玲

（1. 河海大学能源与电气学院，江苏 南京 211100；2. 南瑞集团有限公司（国网电力科学研究院），江苏 南京 211106）

0 引言

目前大规模风电场等值建模已有较多的研究报道［1-3］，它主要包括2个方面的内容，即等值模型结构的确定和等值模型参数的获取。从等值模型结构而言，主要包括单机等值和多机等值。早期在对风电场进行等值建模时，常采用单机等值方法，然而受尾流效应、风电场地形地貌、风速风向等因素的影响，风电场内各风电机组的运行工况不尽相同；同一风电场内的机组类型、机组的控制方式以及参数可能不同，单机等值误差较大，为此文献［4-6］提出多机等值策略。对风电场进行多机等值时，分群是多机等值的前提。传统电力系统进行动态等值时，常基于响应曲线的相似度进行同调判别，最直接的方法是以2 台或以上同步发电机的功角差在观察时段内的最大值小于某设定的阈值，该方法的缺点在于阈值的设定将直接影响分群结果。还有文献通过提取反映受扰轨迹相似度的时频特征进行同调判别。

针对风电机组的分群研究，从基于稳态运行点［7］如风速，到基于单个特征量［4］如桨距角或Crowbar动作与否、风电机组转速、短路容量等，以及基于响应曲线动态特性［2，8-9］的分群等均有报道。文献［3］根据不同风速下风电机组的动态特性，首先将风电场分为3 群，综合特殊运行场景提出将风电场内机组分为4 群的方法。文献［9］提出基于转子电流的同调性进行动态分群的策略。针对电力电子化电力系统，文献［10］提出基于广义哈密顿作用量的同调判别标准，并指出所提哈密顿作用量可表征所有状态的变化趋势。风电机组动态特性的主要影响因素包括以下3 类：机组类型、控制方式及其参数；机组的稳态运行点；机组的受扰程度。风电场动态等值时，既要考虑稳态运行状态的一致性，还要考虑动态特性的一致性。这是由于风功率具有明显的分段特征，为获得较高的稳态拟合效果，需要根据风功率的分段特征将风电机组分群。同时，为获得较高的动态等值精度，还需根据风电机组的受扰轨迹进行同调分群。基于受扰轨迹进行同调分群时，不仅需考虑受扰轨迹的趋势相似性，还需考虑波动相似性。为此，本文提出基于动态时间规整DTW（Dynamic Time Warping）方法［11］寻找相似受扰轨迹，建立聚类指标对风电机组进行同调分群。DTW 方法通过弯曲时间轴增强多个受扰轨迹序列间的形态匹配效果，将其应用于风电机组分群能克服因受扰轨迹的波动和突变等因素而导致相似性失真的问题，有助于搜索到相似度高的受扰轨迹，提高分群精度。

等值机参数的获取是风电场等值建模的另一个重要研究内容。现有研究包括以下2 种途径。一种是“正向”解析方法［12］，即假设已知各台风电机组的自身参数（机型、变流器的控制方式、各组成部分的模型参数等）以及稳态运行情况（如风速、风向等），同时还需已知风电场机组台数、布置方式以及集电网络参数等。将各机组参数通过一定的规则（如按容量加权）进行聚合，从而获得等值机参数。另一种是“反向”辨识方法［13］，它根据系统受扰下的动态量测数据，通过拟合受扰曲线进行参数辨识。基于解析方法获得等值机参数时，等值前要求已知被等值风电场的完整结构、参数以及机组的实际运行工况。由于风电机组参数一般由厂家给定，存在给定值不准确的问题或者由于运行过程中参数发生改变以及人为调节等，所以通过解析方法获得的参数值与实际值可能存在偏差。基于辨识方法获取等值机参数时，存在量测量不充分导致系统不可观、参数的轨迹灵敏度小而难以辨识，亦或参数优化存在多解等问题，因此通过有限的量测获得所有参数的难度较大。尤其当风电场等值为多台机组时，存在参数多且各参数间存在交互影响等现象，通过辨识方法准确获得所有参数的难度较大。

为解决上述问题，本文提出将解析方法与辨识方法相结合的参数获取新思路。先根据风电厂商给出的参数典型值，结合风电场内机组的运行状态以及机组分布等信息，通过解析方法获得等值机参数的初始估计值；再根据风电场在受扰下的动态轨迹，对等值模型中的重点参数进行辨识，辨识时将解析方法获得的参数值作为初始值。当风电场采用多机表征时，系统受扰轨迹与多台等值机参数密切相关。由于参数较多，且参数间可能存在交互影响，如何通过辨识方法获得多等值机参数是难题之一。文献［14-15］研究了同时辨识多台同步发电机参数的策略。与同步发电机相比，双馈风电机组的参数更多，各组成模块的时间常数差别更大。为此在辨识前需确定重点参数，其次需要分析各参数的可辨识性。

综上，本文提出了综合模型聚合和参数辨识的风电场多机等值建模框架，创新性地提出了综合稳态特性与动态特性的风电场分群方法，将DTW 方法引入受扰轨迹的相似度分析。基于轨迹灵敏度方法研究了多等值机的重点参数及参数可辨识性，最后提出了分类辨识和重点辨识相结合的多等值机参数整体辨识策略。

1 综合解析及辨识方法的风电场等值建模整体框架

风电场多机等值时，为准确获得多台等值风电机组的参数值，本文提出将解析方法与辨识方法相结合的建模策略，具体流程见图1。结合“正向”解析方法及“反向”辨识方法2 个步骤，可获得较为准确的风电场等值模型参数。

图1 风电场等值建模流程Fig.1 Flowchart of equivalent modelling for wind farm

2 风电机组的分群

风电场动态等值时，不但需要保持等值前后初始潮流（稳态运行点）相等，还需保证受扰轨迹的高度一致性。

2.1 考虑稳态一致性的风电机组分群

风电场内一般有成百台甚至上千台风电机组，风电机组的位置、风速、风电场的地形等都可能导致各风电机组所受风速不同。由于风电机组的机械功率与输入风速的三次方相关，附录A 图A1展示了仿真得到的双馈风电机组机械功率与输入风速的三次方之间的关系曲线。由图可以看出：风电机组的功率特性具有明显的分段特征，风速位于BD段与位于DE段机组的风功率特性差别较大。如果等值建模时将风电场等值成单台机组，势必造成等值机输入风速的不准确，带来较大的稳态误差。因此风电场等值建模时，为保证等值前后稳态运行点的一致性，可根据各台机组的输入风速，将风速位于BD段的机组分为同群，而风速位于DE段的机组分为另外一群。

对于处于BD段的风电机组，风电机组捕获的机械功率PT可表示为：

式中：ρ为空气密度；R为风轮叶片的长度，πR2为风轮叶片的扫风面积；Cp(λ，βw)为风能利用系数，λ为叶尖速比，βw为风力机叶片的桨距角；v为风电机组输入风速。

由式（1）可以看出：风电机组机械功率与风速的三次方成正比，因此如果按照风速的三次方求取等效风速，等值机的总功率与每台等值机的功率呈线性关系，为此等值机的等效风速veq可用式（2）进行求取。

式中：下标eq 表示等值机组；下标i表示第i台机组；N为同群内的机组台数；Si为第i台风电机组的额定容量；Seq为同群内所有机组的额定容量之和。

而由于风速在DE段的功率特性曲线是一条水平线，因此可以将风速在DE段内所有机组的风速均视为等值风速，取风速在DE段内所有机组的风速按容量加权值作为等值机的输入风速，见式（3）。

2.2 考虑动态特性一致性的风电场分群

当风电机组类型、控制方式或参数存在差异时，其受扰轨迹波形也不尽相同。本文提出基于DTW方法分析受扰轨迹的相似性，该方法允许时间轴上的规整，通过寻找序列之间的最优映射来计算相似度。将其应用于风电机组分群能克服因受扰轨迹的波动和突变等因素而导致相似性失真的问题，从而提高分群精度。基于DTW 方法的受扰轨迹相似性分析的流程如下。

设有2 个受扰轨迹时间序列X=［x1，x2，…，xα］和Y=［y1，y2，…，yβ］，其中α和β为两序列长度。首先定义一个α×β阶的距离矩阵D，其中第m行n列元素表示为d（m，n）=（xm-yn）2。

定义规整路径W如式（4）所示，用来表示序列X和Y的一种对齐或映射，具体如图2所示。

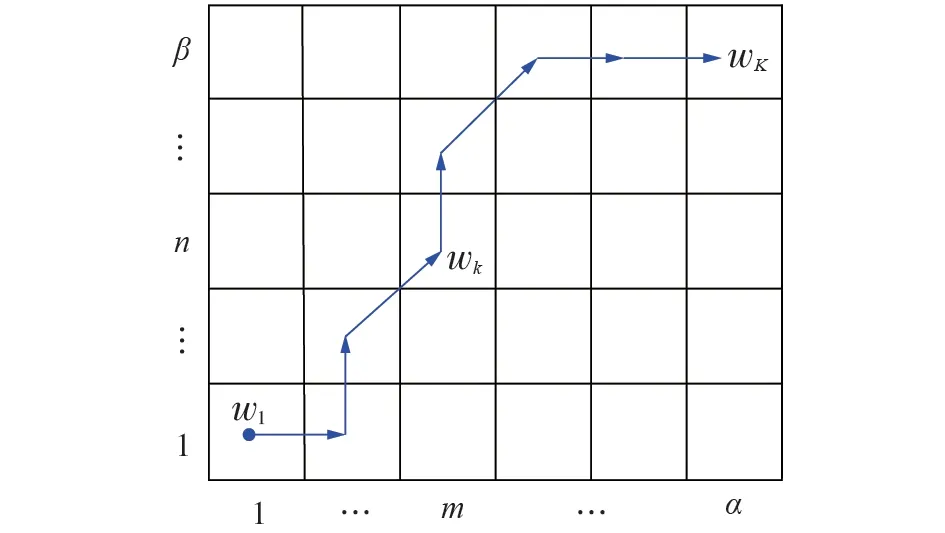
图2 规整路径的原理图Fig.2 Principle diagram of warping path

式中：wk=（m，n）；K为路径长度，且max{α，β}≤K＜α+β-1。

规整路径需满足如下约束：

1）边界性约束，路径的起始点为w1=（1，1），终止点为wK=（α，β）；

2）连续性和单调性约束，若wk=(m，n)，则wk+1前进的方向必须是(m+1，n)、(m，n+1)和(m+1，n+1)中之一。

满足上述约束的路径有很多，将其中累计距离最小的确定为序列X和Y间的DTW 距离，累计距离r(m，n)定义为：

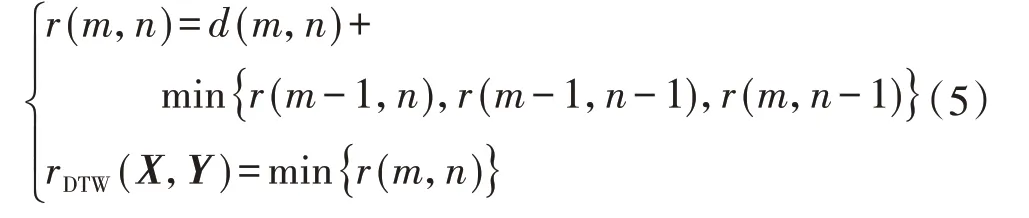
式中：rDTW(X，Y)为序列X和Y间的DTW距离。

2.3 综合稳态特性和动态特性的风电机组分群

为保证等值前后风电场初始潮流的一致性，根据风电机组的功率分段特征可将风电场分为1 至2群；根据等值前后动态特性的一致性，风电场可分群为1 至多群。综合考虑初始潮流一致性和动态特性一致性，风电场最终可分为1至多群不等。

图3展示了稳态分群数为2、暂态分群数为2，且稳态分群和暂态分群不一致时的风电场最终分群结果，其他情形依此类推，不再赘述。图中，Cs1表示稳态分群1 的结果，Ct1表示暂态分群1 的结果，其他类似。

图3 综合稳态和暂态特性的分群结果Fig.3 Grouping results considering steady-state and transient-state characteristics comprehensively

3 等值风电机组模型参数获取的解析方法

3.1 等值风电机组参数的求取

当各台风电机组的参数已知时，等值风电机组的参数xeq可按如下容量加权方法获得：

式中：xi为第i台风电机组参数。

3.2 集电网络的等值参数

文献［16］给出了风电场集电网络的2 类等值方法：一类是在集电网络拓扑结构及参数已知的情况下，以网络变换前后风电机组端口电压不变为原则，对集电网络进行的并联化变换方法；另一类是在拓扑及参数未知时，以风电场聚合前后功率相等为原则，对集电网络进行单阻抗等效。

REI（Radial，Equivalent and Independent）等值方法是电力网络等值的经典方法，可将其用于风电场集电网络等值［17］，其优点在于：精度高，可实现任意分群下的等值。具体流程如下：①将同群内各风电机组的端口电压模值和相角平均，作为等值机母线电压的模值和相位；②将各风电机组出口母线通过一台具有复变比的理想移相变压器连接到等值母线上，理想变压器的复变比为风电机组的出口电压／等值母线电压；③消除各风电机组出口之间的关联支路，转化为连接在相关母线上的对地支路；④保留等值机端口节点以及并网点PCC（Point of Common Coupling），通过网络化简获得集电网络等值模型参数。

4 等值风电机组模型参数的辨识方法

以双馈风电机组为例讨论风电场的多机等值，需要说明的是本文方法同样适用于直驱型风电机组。双馈风电机组包括风力机、传动系统、发电机、变流器以及控制环节，其各组成部分模型结构见文献［16］，其中转子侧变流器的模型结构见附录A图A2。

4.1 重点参数的确定

即使对于单台风电机组，依靠单一扰动一般很难辨识所有参数。为此文献［18］提出分步辨识的方法，采用不同类型的扰动辨识对应扰动下的强相关参数。实际风电场中一般所受扰动为电网侧故障，该故障将直接影响风电场的端口电压。文献［19］根据电网侧电压跌落下有功功率及无功功率受扰轨迹的灵敏度，指出此时灵敏度较大的控制器参数为转子侧变流器有功外环控制器的比例系数Krp_p和积分系数Krp_i，以及电压外环控制器的比例系数Krv_p和积分系数Krv_i（定电压控制方式），或者无功外环控制器的比例系数Krq_p和积分系数Krq_i（定无功控制方式），双馈发电机的定子漏感Ls、转子漏感Lr以及定转子互感Lm。文献［16］指出由于参数Ls和Lr无法区分辨识，本文将两者之和Ls+Lr作为重点参数。

4.2 等值机参数的可辨识性分析

为探讨同时辨识多台等值机参数的可能性，以图4 所示的WTeq1和WTeq2这2 台等值风电机组接入无穷大系统为例，讨论等值机参数的可辨识性。

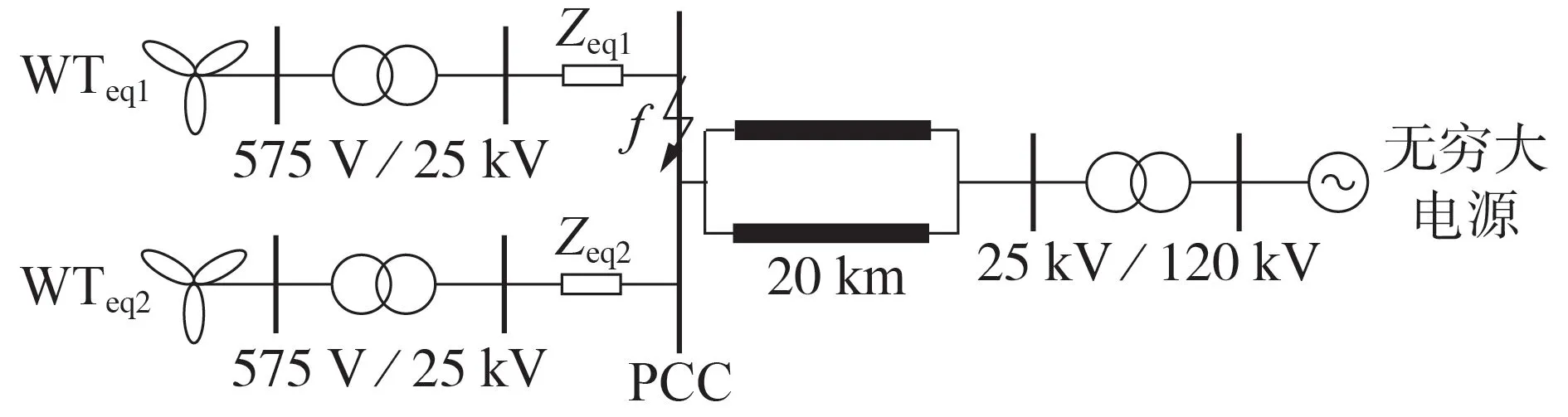
图4 两机系统的示意图Fig.4 Schematic diagram of two-machine system

假设2 台等值机的型号相同，但控制方式不同（分别采用定电压控制和定无功控制），则定电压控制方式下等值机的重点参数为｛Krp_p，Krp_i，Krv_p，Krv_i，Ls+Lr，Lm｝，定无功控制方式下为｛Krp_p，Krp_i，Krq_p，Krq_i，Ls+Lr，Lm｝。为分析多等值机中各重点参数的可辨识性，本文采用轨迹灵敏度方法［20-21］，以故障下PCC 处的有功功率及无功功率作为观测变量，根据各参数的轨迹灵敏度相位判断参数的可辨识性［16，22］。

参数θj的轨迹灵敏度Sθj定义如下：

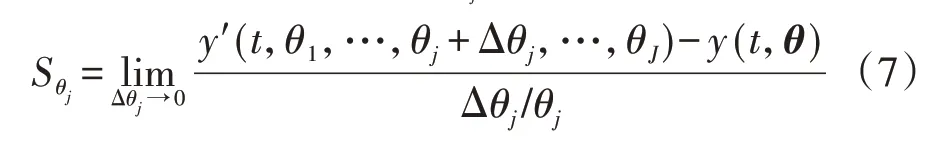
式中：下标j表示第j个参数；J为参数个数；Δθj为θj的变化量；θ为由重点参数所组成的列向量；y和y′分别为原受扰轨迹和参数发生偏差后的受扰轨迹。

假设第j个参数θj与第l个参数θl线性相关，可表示为：

从式（9）可以看出：若参数θl与θj线性相关，则它们的轨迹灵敏度将同相（η＞0）或反相（η＜0）。因此，当2 个或以上参数的轨迹灵敏度相位相同或相反时，这些参数线性相关，无法区分辨识。

4.2.1 相同控制方式下同一参数的可辨识性

设图4中WTeq1和WTeq2型号相同、控制方式也相同，需要说明的是，算例中设控制方式为定电压控制，其他控制方式下所得结论相同，不再赘述。WTeq1和WTeq2的额定容量分别为6 MW 和3 MW，初始风速分别为14 m／s 和12 m／s，Zeq1为Zeq2的1/2。扰动设置为t=0 s 时PCC 处发生三相短路故障，故障期间PCC 处电压降落至65%UN（UN为额定电压），t=0.15 s 后故障消失。分别计算2 台等值机参数的轨迹灵敏度，见图5。图中，SP和SQ分别为各参数对应的有功功率和无功功率轨迹灵敏度。

从图5 可见：采用相同型号、相同控制方式的风电机组，同一参数的轨迹灵敏度基本同相，难以区分辨识；等值机额定容量越大，参数的灵敏度越大。因此在多等值机参数辨识时，将同型号且采用相同控制方式的等值机参数设为一样，并同时辨识。

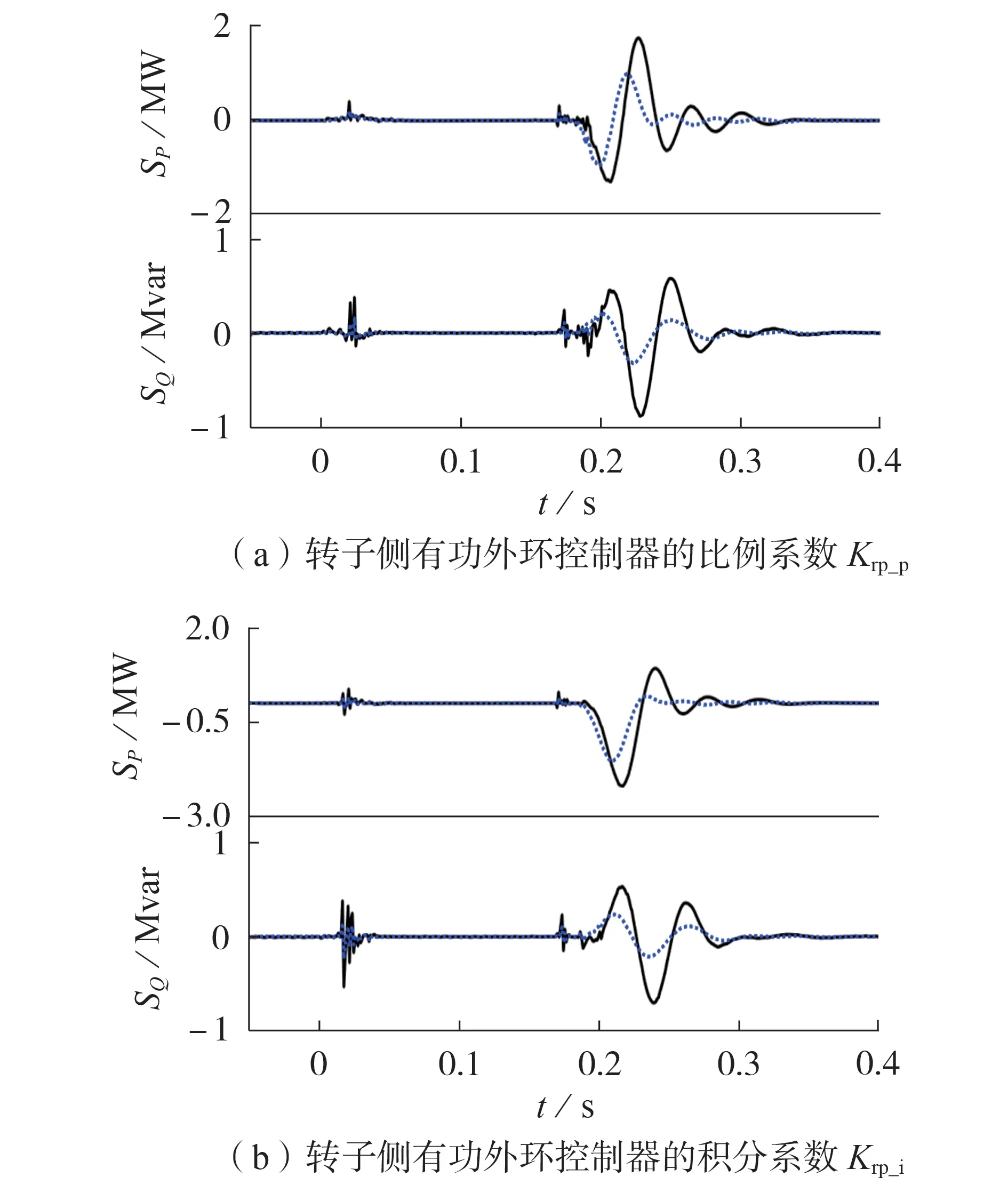
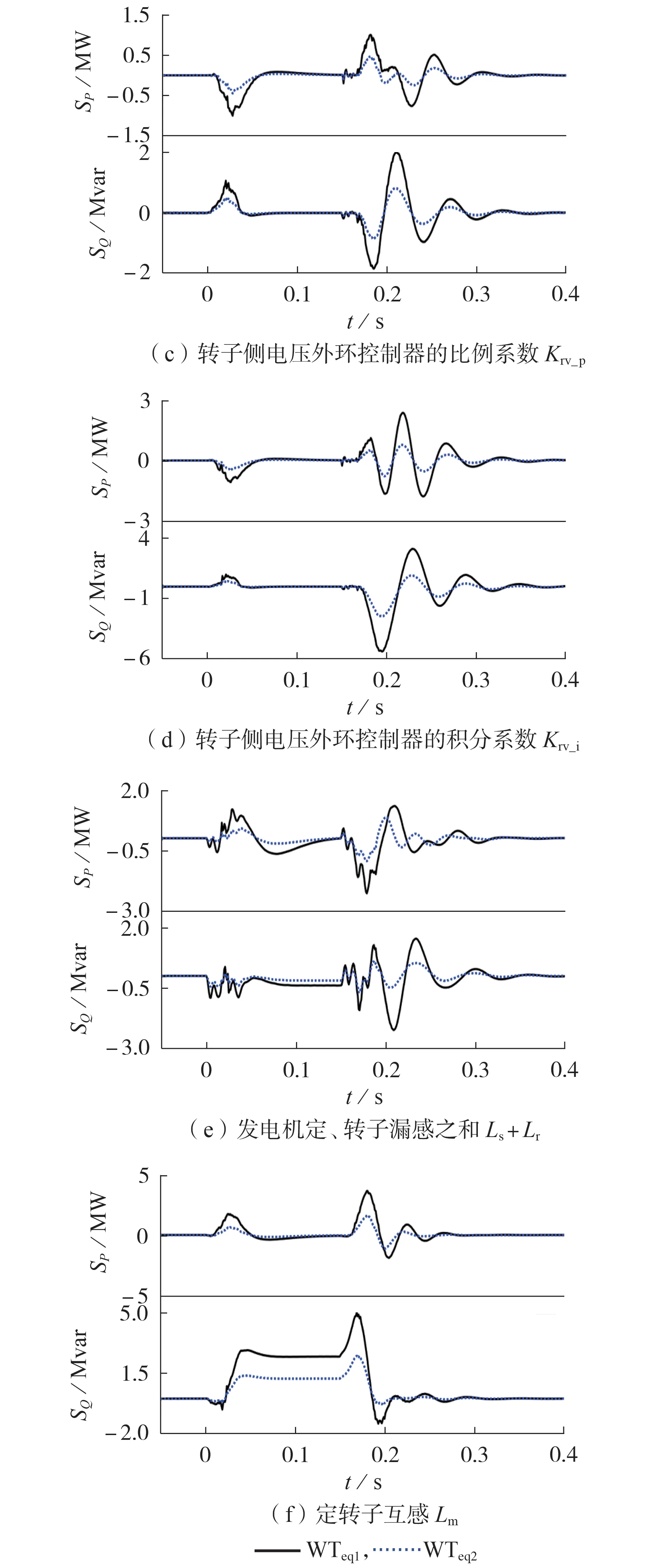
图5 定电压控制下各参数的轨迹灵敏度曲线Fig.5 Trajectory sensitivity curves of each parameter under constant voltage control

4.2.2 不同控制方式下同一参数的可辨识性

设WTeq1和WTeq2的型号相同，但控制方式不同（WTeq1为定电压控制，WTeq2为定无功控制），相同参数的轨迹灵敏度曲线见附录A 图A3。由图可见：采用不同控制方式的两风电机组，同一个参数的轨迹灵敏度不同相，可区分辨识。因此对于采用不同控制方式的2 台或以上等值机，其同一个参数可联合辨识。由图5 和图A3 还可以看出：额定容量越大的等值机，参数的轨迹灵敏度越高，参数越容易辨识。下面进一步分析集电网络等值阻抗的影响。

4.3 集电网络等值阻抗的影响

设WTeq1和WTeq2的额定容量相同（均为6 MW），且型号、控制方式一致，但集电网络等值阻抗不同，其中Zeq1较小，Zeq2较大，以转子侧外环有功控制器的比例和积分系数为例，分析不同等值阻抗下参数的轨迹灵敏度，见附录A 图A4。由图可以看出：额定容量相同但等值阻抗较小的等值机，参数的轨迹灵敏度越高，越容易辨识。

通常情况下等值机的额定容量越大，集电网络参数聚合时由于并联支路较多，其等值阻抗小，此时该等值机组参数的轨迹灵敏度较高，较容易辨识。因此在多等值机参数辨识时，应重点关注额定容量较大的等值机。

4.4 多等值机参数的整体辨识策略

当风电场内机组分为2 群或以上时，由于每台等值机的重点参数较多，若同时辨识所有参数，则由于参数较多可能导致难以收敛，且存在当机组的机型、控制方式相同时，相同参数难以区分辨识的问题，为此本文提出多等值机的参数整体辨识策略，具体如下。

1）分类辨识。对等值机进行分类，认为每类等值机参数相同。分类的主要依据是风电机组类型和控制方式，如采用定电压控制的机组归为一类，采用定无功控制的机组归为另一类。

2）重点辨识。选择重点参数进行辨识，对于非重点参数，由于其对动态轨迹的影响较小，这些参数取为典型值，从而减少辨识误差。

3）修正额定容量大的等值机组的等值阻抗。等值阻抗越小，对动态特性的影响越大。为此在参数辨识时，将大容量等值机的等值阻抗选为待辨识参数，对有功功率和无功功率受扰轨迹进行拟合。

5 算例分析

以图6 所示的风电场为例，它由4 行4 列共16台1.5 MW 双馈风电机组通过机端变压器升压至25 kV，通过集电网络连至PCC 母线，再经2 台升压变通过双回线与无穷大系统相连。同馈线机组间距为400 m（Y轴），馈线间距为500 m（X轴），风轮直径为70 m。设机组WT1—WT8采用定电压控制方式，机组WT9—WT16采用定无功功率控制方式。风电机组模型参数见MATLAB／Simulink平台［23］。

图6 风电场的机组分布Fig.6 Layout of wind turbine generators at wind farm

假设风由风电场的左下方吹入，风向为35°（与X轴的夹角），测风塔（位于风机WT1的位置）所测风速为14 m／s，推力系数取0.8，粗糙常数取0.075。

5.1 风电机组的分群

采用文献［7］所提的风速估算方法，根据各风电机组之间的距离及风向，计算上游机组沿风向在下游机组的尾流半径，进一步估算得到风电场内各机组的风速，见表1。

表1 风速分布Table 1 Distribution of wind speed

首先根据风电机组的稳态运行情况分群。由表1 中各机组的风速以及其风速-功率曲线可知，机组WT1—WT5、WT9、WT13运行于恒功率区，其余机组运行于最大功率跟踪区。此时按照潮流一致性的分群结果为：机组WT1—WT5、WT9、WT13为同群，机组WT6—WT8、WT10—WT12、WT14—WT16为另一群。

进一步根据风电机组的动态特性分群。扰动设置为t=0 s 时f3处发生三相短路故障，持续0.15 s后故障消失，系统恢复至原状态。各风电机组有功功率P与无功功率Q受扰轨迹见图7，图中P、Q均为标幺值。

根据图7所示的16台风电机组有功功率和无功功率受扰轨迹的时间序列，采用DTW 方法计算受扰轨迹间的DTW 距离，结果见附录B 表B1。DTW 距离越小，说明受扰轨迹之间的相似度越高。由表B1可以看出：机组WT1—WT8两两之间、机组WT9—WT16两两之间的DTW 距离较小；机组WT1—WT4相对机组WT5—WT8间的DTW距离稍大，但不明显，这是由于机组WT1—WT4与机组WT5—WT8的稳态运行点不同，且与故障点的距离不同；机组WT1—WT8相对机组WT9—WT16间的DTW 距离较大（见表B1中的阴影部分），这是由于机组WT1—WT8和机组WT9—WT16的控制方式不同。

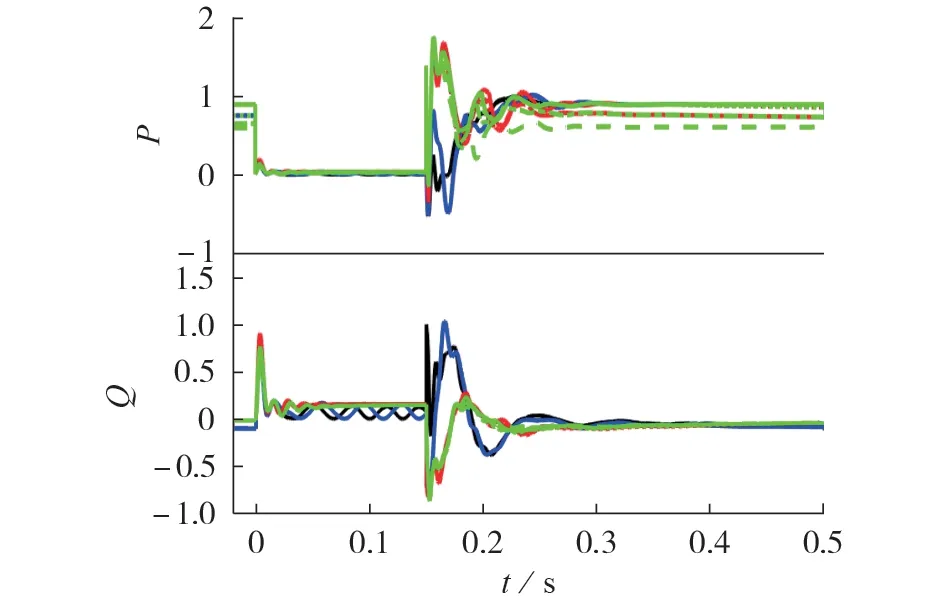
图7 f3 处发生三相短路故障时各风电机组的受扰轨迹Fig.7 Disturbed trajectories of wind turbine generators under three-phase short circuit fault at f3

根据DTW 相似度结果可知：WT1—WT8的受扰轨迹相似度较高，可分为同群；机组WT9—WT16的受扰轨迹相似度较高，可分为另一群。DTW 的分群结果与机组控制方式相吻合，说明了DTW 分群方法的可行性。为进一步说明DTW 动态分群方法的有效性，附录B 还给出了风电场内各机组参数存在差异情况下的分群结果。

综合稳态分群以及DTW 相似度结果，可得风电场的最终分群结果见表2。各等值机的等值风速可根据式（2）计算得到。

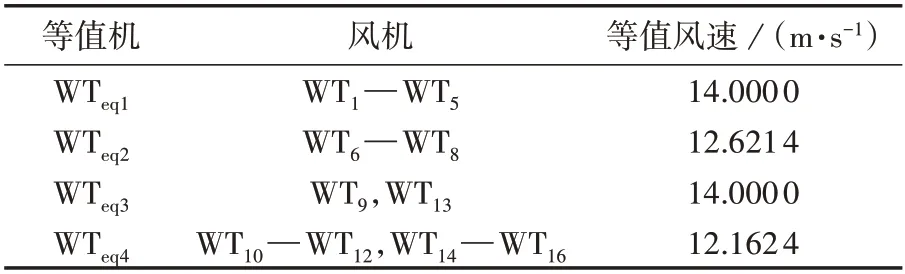
表2 风电机组分群结果Table 2 Grouping results of wind turbine generators

5.2 集电网络的参数聚合

根据表2 所示的分群结果，采用REI 方法对图6所示的风电场进行集电网络等值，可得风电场多机等值模型结构，如图8 所示。图中等值机WTeq1和WTeq2之间、WTeq3和WTeq4之间分别存在联络线等值阻抗Zeq12和Zeq34的原因在于非自然馈线分群。通常等值机的机端电压相差不大，因此可将Zeq12和Zeq34忽略。根据REI等值结果可得：Zeq1=1.9402+j6.1685 Ω，Zeq2=2.5962+j8.2692 Ω，Zeq3=312.13+j937.5 Ω，Zeq4=1.3045+j4.1228 Ω。

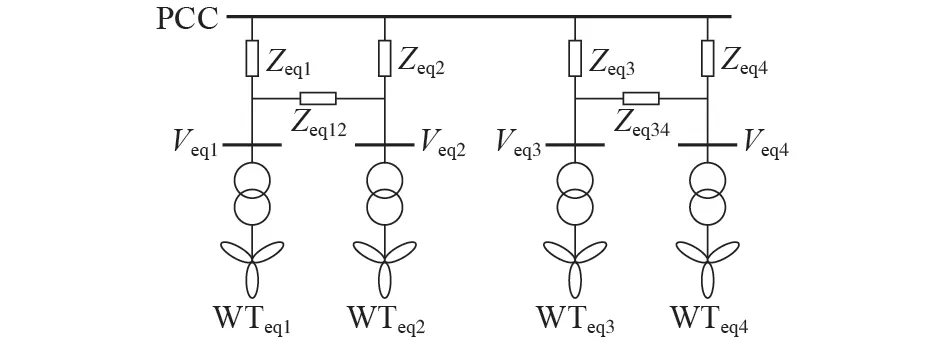
图8 风电场的多机等值模型结构Fig.8 Structure of multi-machine equivalent model for wind farm

5.3 等值风电机组的参数辨识

首先根据分类辨识的原则，由于等值机WTeq1和WTeq2都采用定电压控制，认为WTeq1和WTeq2的参数相同；等值机WTeq3和WTeq4都采用定无功控制，认为等值机WTeq3和WTeq4的参数相同。根据重点辨识原则，可得等值机WTeq1和WTeq2的重点参数为｛Krp_p_eq，Krp_i_eq，Krv_p_eq，Krv_i_eq，（Ls+Lr）_eq，Lm_eq｝，等值机WTeq3和WTeq4的重点参数为｛Krp_p_eq，Krp_i_eq，Krq_p_eq，Krq_i_eq，（Ls+Lr）_eq，Lm_eq｝。同时由于等值机WTeq4包含的机组台数多、容量大，选择其等值阻抗进行修正，即将Zeq4也作为重点参数。

将故障设置为t=0 s 时无穷大电源端口（图6 中的f1处）电压跌落至50%UN，持续0.15 s 后故障消失，系统恢复至原状态。先基于解析方法获得各等值机的参数，进一步将PCC 处的有功功率和无功功率受扰轨迹选为观测量，采用粒子群优化算法［24］辨识重点参数。参数辨识目标函数为：

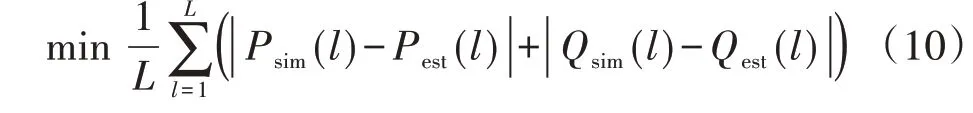
式中：Psim和Qsim分别为基于等值前详细模型仿真获得的PCC 处有功和无功功率；Pest和Qest分别为基于参数值辨识值仿真获得的PCC处有功和无功功率；L为受扰轨迹时间窗口内总仿真步长数。

采用粒子群优化算法进行参数辨识时，设粒子群种群大小为60，最大迭代次数为60，学习因子为2，最小权重系数和最大权重系数值分别为0.4和0.9。表3 为各等值机的参数辨识结果。表中，（Ls+Lr）_eq、Lm_eq均为标幺值。

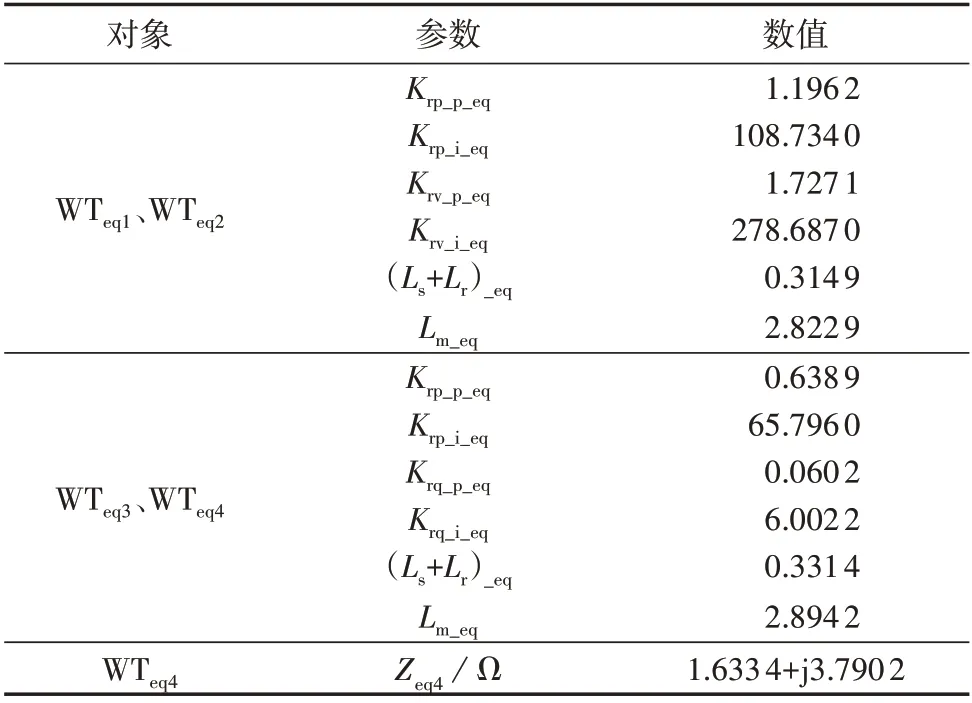
表3 等值风电机组参数辨识结果Table 3 Parameter estimation results for equivalent wind turbine generators

图9 给出了原系统以及基于辨识结果的等值模型在PCC 处的电压U、有功功率和无功功率受扰轨迹，图中U为标幺值。由图9 可以看出：综合解析方法和辨识方法的多机参数获取策略具有较好的动态拟合效果。下面进一步基于其他故障类型，分析上述参数辨识结果的适应性。

图9 f1 处电压跌落至50%UN时的等值结果Fig.9 Equivalent results when voltage drops to 50%UN at f1

5.4 辨识模型的适应性分析

将故障设置为120 kV线路中点（图6中f2处）在t=0 s 时发生三相短路故障，此时PCC 处电压跌落至15%UN。附录C 图C1 给出了原系统以及基于辨识结果的等值模型在PCC 处的电压、有功功率和无功功率受扰轨迹。由图可以看出：在电压跌落较严重情况下，等值模型依然具有较好的拟合精度，说明等值模型具有较好的适应性；比较等值前后有功功率和无功功率受扰轨迹可以看出无功功率受扰轨迹的误差偏大，其原因在于故障点离风电场越近，风电机组动态对等值阻抗越敏感，此时等值模型的误差有所增加。

6 结论

多机等值建模是风电场动态等值的研究重点，然而多机参数的准确获取难度较大。针对该问题，本文提出了综合解析方法和辨识方法的风电场多机等值建模框架。首先基于解析方法获取等值模型的参数值，然后将其作为初始值通过辨识方法获取模型参数。

在对多机模型进行参数辨识时，由于参数较多，存在不可辨识、难以辨识等问题。为此，本文基于轨迹灵敏度方法，分析了参数的可辨识性，在此基础上选取其中的重点参数作为待辨识参数。

最后，本文提出了基于分类辨识、重点辨识的多等值机参数整体辨识策略。基于仿真算例进行了模型验证，进一步分析了模型的适应性。后续研究工作包括不同低电压穿越策略下风电场的多机等值建模，以及基于风电场现场录波数据进行本文方法的实测验证。

附录见本刊网络版（http：//www.epae.cn）。