基于广义斯塔克尔伯格博弈的微电网能源管理

陈雨甜，王秀丽，钱 涛，吴 雄

（西安交通大学电气工程学院，陕西 西安 710049）

0 引言

为了减少环境污染和能源消耗以及提高电能服务质量，传统电网正逐步向智能电网［1］转型，微电网作为分布式电源接入智能电网的有效手段受到广泛关注［2］。微电网是由分布式电源、储能和相关负荷组成的小型发配用电系统，可实现区域内电能的产消一体化，它充分挖掘了分布式能源的价值，提高了电能效益。不同于传统电网中电网向电力用户单向传输电能，在微电网中用户可以向电网传递所需电能信息，从而参与电能的分配［3］。

随着微电网的快速发展，微电网能源管理成为研究热点。有效的能源管理可以引导分布式电源就地消纳，实现能源的有效配置，保证用户侧优质的能源服务，提高系统运行的安全可靠性。现有研究集中于微电网和微电网［4-5］、用户和用户［6-7］、微电网和用户［8-10］间的互动决策，大多基于特定场景展开，如电动汽车、分布式储能装置等。博弈论作为分析多主体交互决策的有力工具，在确定多主体多目标的最优决策中广泛应用。文献［8］建立主动配电网和电动汽车的主从博弈模型，通过电价引导电动汽车充放电，但文中侧重分析配电网和电动汽车的博弈过程而忽略了电动汽车间的影响。文献［9-10］分别基于非合作博弈理论和拍卖理论研究智慧社区中住户和共享设施管理者之间的能源交易，但文献［9］未考虑不同用户差别定价的影响，而文献［10］未考虑双方的参与积极性问题。

在特定的时间和空间下，由于系统资源有限或受到系统安全稳定运行约束等影响，参与微电网能源管理的各主体决策变量满足某些公共约束，此时博弈中的纳什均衡问题NEP（Nash Equilibrium Problem）拓展为广义纳什均衡问题GNEP（Generalized Nash Equilibrium Problem）［11］。文献［12］利用广义纳什均衡理论解决用户的日前调度策略问题，设计一种分布式算法对问题进行求解，以最小化用户用电成本。文献［13-14］考虑所有电动汽车的充电量约束以及能耗约束，建立电动汽车充电的广义斯塔克尔伯格博弈GSG（Generalized Stackelberg Game）模型，合理分配电网以及充电站的可用能源，其中文献［13］利用超平面投影算法求解模型，文献［14］将博弈模型转化为混合整数线性规划问题进行求解。文献［15-16］分别提出一种分布式能源管理和交易方案——分布式能源管理调度（DEMANDS）和电能交易网络拓扑控制（ENTRANT），以解决多个微电网和多个用户之间的能量调度问题，不同的是，在建立的斯塔克尔伯格博弈模型中，文献［15］将用户作为领导者，文献［16］将微电网作为领导者。上述文献中的参与者不仅在效用函数上与其他参与者耦合，而且每个参与者的策略集合与其他参与者的策略有关，因此GNEP 比NEP 更复杂，更难以求解。文献［17］提出几种解决GNEP 的方法，如非线性迭代算法、利用Nikaido-Isoda 函数将其转化为某类优化问题的方法和罚函数法。文献［18］详细分析广义纳什博弈GNG（Generalized Nash Game）和变分不等式VI（Variational Inequality）之间的关系，将GNEP 转化为VI 进行求解。在微电网能源管理中，不同用户之间通常需要共享资源，因此很有必要考虑用户之间的相互影响，但这同时增加了模型的复杂度，使模型不易求解。为了实现微电网能源的优化管理，获得最优的群体效益，本文聚焦一类具有共同约束的广义博弈问题，在微电网和用户的博弈过程中计及用户之间的耦合关系，利用VI 相关理论求解模型，降低了求解难度，提高了求解速度。

在有限参与者的有限行为对策中使所有参与者达到最优策略的组合为纳什均衡。在微电网的电能交易中，每个主体都是理性而自私的，利用纳什均衡理论解决主体之间的利益冲突，使交易达到稳定均衡状态，进而使交易的各主体达到自身收益的最大化，调动各主体参与交易的积极性。本文首先基于非合作博弈理论建立单个微电网和多个用户的GSG模型，其中微电网是博弈的主体，决定单位能源的价格，引导用户积极参与电能交易以及调整用电策略，用户是博弈的从体，每个用户都是理性而平等的参与者，根据已知电价做出购电决策并影响电价的制定，不同用户的博弈策略相互耦合；其次，利用VI 相关理论证明广义斯塔克尔伯格均衡GSE（Generalized Stackelberg Equilibrium）的存在，并通过固定步长的投影算法PACS（Projection Algorithm with Constant Step）和基于高斯-赛德尔的最佳响应算法BR（Best Response algorithm）求解用户之间的广义纳什均衡GNE（Generalized Nash Equilibrium），得到用户的最佳购电策略，并优化微电网电价；最后，通过某社区微电网的相关数据证明所建模型可优化用户的购电量和微电网电价，提升社会整体效益。

1 系统模型

本文考虑孤岛型微电网中用户之间的交互决策，微电网中电能自给自足，与主网无电能交换。微电网中包含多种分布式电源，其通过配电设施直接向微电网中用户供电，减少了电能的远距离传输。微电网中购、售电双方建立自行协商的价格体系进行自主交易。假设微电网一天中可出售的电能总量为E，其值为常量且保持不变，购电用户总数为N，购电用户集合为C，用户n(n∈C)向微电网的购电量为xn。由于特定时间和空间下微电网中产生的电能有限，因此xn应满足式（1）所示的约束。

微电网和用户之间的电能交易过程为：用户根据微电网制定的电价调整购电量，微电网根据用户反馈的购电量重新制定电价。因此，建模的重点在于合理描述每个用户和微电网的效用函数，同时准确模拟用户和微电网之间的交互过程，确定使博弈双方获利最大的电价和用电策略。

1.1 用户的效用函数

用户的效用函数表征用户用电的效能，是用户消耗电能的函数，与用户的购电量、电价、用户满意度和用户用电量有关。每个用户以最大化自身的效用函数为目标，在与微电网的博弈过程中不断改变自身的购电量。根据实际用电情况，用户在达到电能消费上限时会不断地消耗电能，因此用户购电的效用函数是一个不减的非负函数，而用户的购电满意度随着购电量的上升会逐渐趋于饱和，因此用户购电的边际效益是一个不增的函数。在满足式（1）的条件下，定义用户n的效用函数Un为如下二次函数：

1.2 微电网的效用函数

微电网以最大化售电收入为目标制定电价，定义微电网的效用函数为：

2 GSG

2.1 博弈模型

非合作博弈模型广泛应用于分析多主体的交互决策，每个参与者在利益相互影响的局势下，独立做出最优决策。斯塔克尔伯格博弈属于最常见的非合作博弈，参与者按先后顺序选择相应的策略。在本文中，微电网和用户都追求自身效益的最大化，两者依靠电价和购电策略形成主从博弈关系，因此可采用斯塔克尔伯格博弈对其进行描述。其中，微电网是博弈的领导者，通过制定电价引导用户制定用电策略，用户是博弈的追随者，根据已确定的电价不断调整自身的购电量并影响微电网的定价策略。每个用户都是理性而自私的，由于电能资源的限制，所有用户的购电量之和小于E，用户的购电决策相互影响，每个用户的可行策略集与其他用户的策略有关，xn∈Sn(xn，x-n)，其中Sn为用户n的可行策略集。当其余用户的购电策略给定时，用户n通过最大化Un在自身策略集下确定最佳购电策略xn。微电网和用户的博弈过程如图1所示。

图1 微电网和用户的博弈过程Fig.1 Game process of microgrid and consumers

2.2 GSE

在上述博弈模型中，微电网通过电价对用户的购电策略进行管理，每个用户在给定的电价下选择合适的购电量从而最大化自身的效用函数，因此当p确定时，用户n的目标函数为：

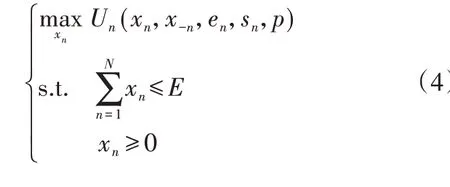
实际上，从式（1）所示的约束可以看出用户n的购电量xn不仅与电价以及用户自身的用电策略有关，还与其他用户的购电量x-n有关。用户之间形成GNG，当x达到GNE 时，任一用户单独改变购电策略都不会再得到更好的结果。当得到用户更新后的购电策略后，微电网据此更新电价，从而最大化自身收益，其目标函数为：

2.3 变分解的存在性和唯一性

GSG 问题的纯策略不一定存在，而GSE 的存在性是提出2.1 节中问题Γ的基础。证明GSE 的存在性即证明用户间GNE 的存在性，GNE 即使存在，通常也不止1 个解，此时难以确定用户的最佳购电策略集合。当GNEP 中的所有目标函数连续可微并对相应的决策变量伪凸，且决策空间是封闭凸集时，具有公共约束的GNEP 可以转化为VI 进行求解，称为变分解VE（Variational Equilibrium）。因此GNE和GSE 存在性的证明转化为VE 存在性和唯一性的证明。VI(K，F)是在h维欧氏空间Rh的闭凸集K上确定一个向量y*∈K，该向量满足不等式FT(y*)(yy*)≥0(∀y∈K)，其中F为定义在K上的连续函数。在问题Γ中GNE满足以下方程：

式中：S为所有用户的决策空间；F(x)为所有用户效用函数的相反数关于自身购电量的偏导数，即F(x)=-(∇xUn(x))n∈C。

定理1 对于2.1 节中定义的GSG 问题Γ，有且仅有1个VE。证明如下。

所有用户的决策空间S是封闭凸集，效用函数Un连续可导且是严格凹函数，根据效用函数Un的定义，其满足对用户购电量xn的偏导数不小于0，同时对xn的偏二次导数不大于0，因此VI 至少存在1 个解VE，VE同时也是GNEP的均衡解，则相应的GSEP至少存在1个GSE。

由于sn＞0，因此JF＞0，JF正定，F严格单调，VI至多有1个解。

综上所述，VI 有且仅有唯一解VE，则GNEP 存在稳定解GNE，当GNE 确定后，微电网有唯一p*使GSEP达到GSE。

3 模型求解

3.1 GNE求解

当微电网价格p给定时，用户之间购电策略的博弈转化为GNEP，基于GNEP 和VI 的等价性，可以利用求解VI的方法求解相应的GNEP。将带有公共约束的GNEP 转化为带惩罚因子λ（λ为所有拉格朗日乘子组成的向量）的NEP：

3.2 电价优化

当用户之间的博弈达到GNE 后，微电网可通过用户的购电策略优化电价。由式（12）可知VE 满足式（17）。

4 算例分析

本文以某社区微电网为例，应用建立的GSG 模型，通过社区微电网的动态定价策略引导用户的电能消费，并利用所提算法实现用户之间购电量的GNE。该社区微电网中包含多种分布式电源和多户居民用户。其中分布式电源包含微型燃气轮机、光伏板等，额定容量均在10～100 kW 之间；居民用户购电满足日常用电需求，家用电器的额定容量均在50～2000 W之间。由于特定时间和区域的限制，微电网产生的电能有限，用户直接向微电网购电，购电总量不超过微电网可售电量，从而形成式（1）所示的约束。以每10 户为1 个单位，即当n=1 时认为包含10户用户，根据普通居民用户的用电情况，每户居民预估用电量en的取值范围为35～70 kW·h，sn的取值范围为1～2。首先设置用户总数N=5，微电网可售电量E=180 kW·h，初始电价p()0=0.3 元／（kW·h），用户的基本参数如附录A表A1所示。每户用户由于自身的用电习惯不同，en和sn均各不相同。

利用PACS 和BR 求解模型，则用户购电量和微电网电价分别见图2和图3。从图中可以看出，所提算法均有效收敛，收敛速度较快。在微电网和用户的相互博弈过程中，用户根据电网电价调整自身用电策略，微电网通过电价引导用户选择最优的购电方案，鼓励用户参与电量交易，提高售电利益，最终微电网和用户都获得了最优方案，用户的最优购电策略为x*=［8.6399，33.0665，17.2234，35.3798，43.7089］kW·h，微电网制定的最佳电价p*=0.4405元／（kW·h）。

图2 用户购电量Fig.2 Electricity consumption of consumers

图3 微电网电价Fig.3 Electricity price of microgrid

图4 和图5 分别体现了微电网可售电量E和用户总数N对微电网电价的影响。在图4 中设置N=5、p()

图4 微电网可售电量对微电网电价的影响Fig.4 Influence of available electricity sales of microgrid on electricity price of microgrid

0=0.3 元／（kW·h）。由图可见，在不同的E值下电网电价均收敛到有效值，随着E的增加，p*降低，由于微电网可售电量增加，因此适当降低电价也可保证相应的收入，且由于用户之间通过式（1）相互耦合，购电量之和不能超过E，E增加则用户间的竞争减小，用户的购电量将相应增加，微电网可以降低电价吸引用户参与电能交易。在图5中设置E=180 kW·h、p()

图5 用户数对微电网电价的影响Fig.5 Influence of number of consumers on electricity price of microgrid

0=0.3元／（kW·h）。由图可见，在不同的N值下电网电价均能收敛到有效值，随着N的增加，p*提高，这是由于当微电网可售电量一定时，N越大，则博弈的参与者越多，竞争越激烈，每个用户的购电量相应减少，在电能资源有限的情况下，为保证合理收益，微电网适当提高电价。

为了突出本文所提算法的有效性和优越性，与文献［13］中算法进行对比。文献［13］利用超平面投影法求解GSG，算法原理较为复杂。在同等条件下，利用不同算法得到各用户的效用函数，如图6 所示。由图可见，当模型达到GSE时，在本文算法下各用户的效用函数更大。此外，在迭代过程中，本文算法在10 次内即收敛到GSE，而文献［13］算法需迭代20 次左右才能收敛到GSE。

图6 不同算法下各用户的效用函数Fig.6 Utility function of each consumer under different algorithms

5 结论

本文聚焦于微电网和用户的动态博弈过程，首先介绍微电网和用户的效用函数，建立二者交易的GSG模型，其中微电网是博弈的领导者，决定单位能源价格，激励用户参与电能交易以及调整用电策略，用户是博弈的追随者，根据已知电价做出购电决策，并影响电价制定，且不同用户的博弈策略相互耦合；然后利用GNE 的相关理论，将博弈均衡解的求解转化为VE 的求解，并基于一类GNEP 和VI 的等价性，利用PACS 和BR 求得用户购电策略的GNE，进而求解最优电价；最后通过某社区微电网的实例验证了所提模型和算法的可行性和有效性，分析了微电网可售电量和用户总数对微电网电价的影响。本文利用博弈论的相关理论研究微电网和用户之间的能源交易，有利于实现微电网的实时能源管理，提升社会效益。同时，本文所提出的考虑用户耦合约束的模型和求解算法可适用于电动汽车充电、用户需求侧管理、点对点能源交易等多种场景，未来可以进一步考虑微电网和主网的互动，研究大电网、微电网和用户之间的能源交易模式。

附录见本刊网络版（http：//www.epae.cn）。