模块化多电平矩阵变换器的平坦控制策略

程启明，谢怡群，马信乔，江 畅，赵淼圳

（上海电力大学自动化工程学院上海市电站自动化技术重点实验室，上海 200090）

0 引言

在所有可再生能源发电中，风力发电已经成为增长最快和最大的产业。全球的风电装机容量从2000 年的17.4 GW 迅速增长到2015 年的432.4 GW，使风能成为中国、美国以及欧洲等地区重要的关键能源［1］。欧洲风能协会表示：“风电到2030 年将占30%，到2050年将达到50%。”

由于海上具有更大的可用空间和较高的风能潜力［2］，许多风力发电项目位于海上。下一代海上风电机组的位置预计将离岸边达300 km，而一个重要的技术问题是如何将海上发电厂与主电网并网。目前有3 种解决方案，即50 Hz 的高压交流输电［3］、高压直流输电［4］和50/3 Hz 的低频交流输电［5-6］。海上风电跨海输电线路一般为电缆，电缆中三相线路排列紧密，相比于架空线路，其线路的电抗降低而电容增加，若使用传统的高压交流输电方式进行并网，线路中容性电流会较大，使得线路损耗增加并会导致线路容量堵塞［7-8］。因此，高压交流输电方式一般只应用于近海上风电场并网。对于中远距离风电场，目前一般使用高压直流并网［9-10］。使用高压直流输电技术可以避免电缆电容的影响，增大电能传输容量和距离，但其所需的换流站和海上汇流平台需要昂贵的费用进行建设和维护。虽然高压直流输电方式下电缆线路损耗较低，但在传输过程中多步换流产生的总损耗要高于高压交流输电方式。低频交流输电具有以下优势［11］：与传统50 Hz 的高压交流输电相比，较低的电网频率大幅降低了输电线路阻抗，极大地提高了输电效率；与高压直流输电相比，低频交流输电只需建立1 个AC／AC 换流站，建设和维护费用要便宜得多。低频交流输电中最重要的设备是AC／AC 变换器，为了达到AC／AC 变换的目的［6，12-15］，可采用文献［12］中的2 个背对背模块化多电平变换器（MMC）系统，但是这会增大设备体积和成本。为此，美国Colorado 大学的Erickson R.和AI-Naseem O.于2001 年提出了一种新型的级联H 桥AC／AC 变换器——模块化多电平矩阵变换器MMMC（Modular Multilevel Matrix Converter），也称为M3C［13］。

M3C 是由许多H 桥单元串联成双向开关，并不是传统的矩阵变换器中的半导体开关器件，具有完全模块化、易于扩展到高电平、控制灵活、谐波质量好、冗余度好等优点［6，14-15］。这些独特的优势使它非常适用于大功率风能转换系统［14］。但是，M3C 的非线性、强耦合等特点导致其控制十分复杂，发展也异常缓慢。目前，M3C的研究仍处于理论研究阶段，且国内外还没有成熟的应用。在M3C 控制方面的研究，目前主要有：M3C 输入侧的控制［16-18］、M3C 电容电压和桥臂环流的控制［19-23］以及M3C 输出侧的控制［18，23-24］。对于M3C 电容电压控制的研究较多，如文献［19］基于矢量控制提出注入循环电流，文献［20］提出桥臂电容电压的能量平衡控制，文献［21-22］采用基于空间矢量脉宽调制（PWM）的输入／输出电流控制和直流侧电容平衡控制等。而对M3C 输入侧的控制研究极少，目前主要是比例积分（PI）控制［16-18］。文献［24］提出了双αβ0 变换，实现了输入侧电流、输出侧电流以及桥臂环流从9 个桥臂电流中的分离，即实现了解耦控制，但输入侧电流采用了PI控制，其控制效果并不令人满意。

本文基于M3C 在双αβ0 变换下的解耦模型，在文献［25-28］的启发下，根据基于双αβ0 变换下的解耦模型，提出了基于微分平坦理论的M3C 输入侧控制，相比于传统PI 控制策略，根据微分平坦理论设计的平坦控制器可解决变换器受到内、外部扰动时动态特性变差的问题［27］，而且其突出优势在于利用系统参考平坦输出进行空间轨迹跟踪［26-27］，对系统的参数变化及外来摄动有较强的鲁棒性［28-29］，无需精确的线性化模型就能稳定、精确地控制M3C 的输入侧［30］。基于微分平坦理论设计的平坦控制系统具有结构简单、控制效果好、实现容易的优点，仿真结果也证明了本文所提平坦控制策略的正确性和优越性。

1 M3C的电路结构和数学模型

1.1 M3C的总体结构

M3C 的拓扑结构如附录A 图A1（a）所示，其由9 个桥臂组成，每个桥臂都由k个H 桥子模块SM（Sub-Modular）串联后再串联1 个电感Lqb组成。每个H 桥子模块都由1 个H 全桥和1 个直流电容C并联而成，每个H 全桥都由4 个IGBT（T1—T4）反并联二极管组成。M3C的输入侧与输出侧均为三相交流对称系统，输入侧通常为三相对称交流电压源，输出侧一般连接电动机、阻感负载或者电网等。M3C 的简化模型如附录A图A1（b）所示。

图1 为M3C 总体控制框图。由图可见，M3C 的控制系统主要由输入侧控制、桥臂电容电压控制和桥臂环流控制、输出侧控制、共模电压控制以及H桥子模块的均压控制等控制模块组成。输入侧控制主要是通过采集M3C 输入端口mx（x=a，b，c）的三相电压umx和三相电流imx，先经αβ0变换再经dq变换即可得到输入侧的传统控制方法，即PI 控制（详见2.1节），而本文则是分析其输入侧数学模型的平坦性，依据微分平坦理论设计的平坦控制器，其具体理论分析与推导过程见2.2 节。桥臂电容电压控制和桥臂环流控制是通过建立M3C 的功率-电容电压模型，经双αβ0变换，通过设计环流以调节其中可能的直流漂移，继而实现桥臂环流控制。输出侧控制是通过采集M3C 输出端口gy（y=r，s，t）的三相电压ugy和三相电流igy，先经αβ0 变换再经dq变换即可得到输出侧的PI 控制律。共模电压控制是通过注入共模电压unN来控制桥臂电容电压平衡，文中已采取“设计环流”的方法，故无需再考虑注入共模电压，即令unN=0。H 桥子模块的均压控制是通过采集xy桥臂上的电流ixy、xy桥臂总电容输出电压uCxy及xy桥臂上第z（z=1，2，…，k）个H 桥子模块的电容电压，结合输入侧、桥臂及输出侧的控制信号即可得到H 桥子模块的均压控制律。

图1 M3C总体控制框图Fig.1 Overall control block diagram of M3C

1.2 M3C的数学模型

根据附录A 图A1 的电路模型，依据基尔霍夫电压定律（KVL）可得：

式中：umo、imo、ugo、igo分别为umx、imx、ugy、igy变换到αβ0坐标系下的量，且o=α，β，0；uop、iop分别为uxy、ixy变换到双αβ0坐标系下的量，且p=α，β，0。

将式（17）和式（18）代入式（4），可得：

2 M3C的输入侧控制

M3C 输入侧电流若不经过控制，则会导致M3C的输入侧三相电流严重不对称。目前对于M3C 的输入侧电流采取的控制策略主要是PI 控制策略，但是PI 控制存在产生超调、稳定速度慢、动态性能差的缺点，因此本文提出一种新型的控制策略，即基于微分平坦理论设计的平坦控制策略。

2.1 传统PI控制策略及其缺陷

根据式（19）可得M3C 的输入侧在dq坐标系下的数学模型为：

由于传统PI 控制策略的控制效果并不令人满意（见3.1节中分析），因此本文根据微分平坦理论提出平坦控制策略。基于微分平坦理论设计的平坦控制系统具有响应速度快、输出波动小、跟踪无静差、动态性能好等优点。

2.2 微分平坦理论及其优势

为更好地解决非线性系统的控制问题，Flies 于20 世纪90 年代提出微分平坦理论。下面分析其基本原理。

设非线性系统为：

式中：x、y、u分别为非线性系统的状态变量矩阵、人为选取输出变量矩阵、输入变量矩阵。

若非线性系统存在一组输出量满足式（24），则该非线性系统满足微分平坦理论［25］。

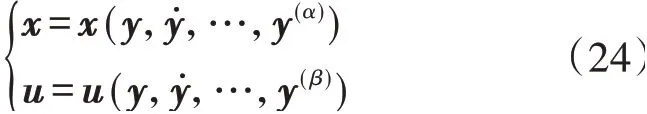
式中：α、β为正整数，表示微分阶数。

基于微分平坦理论的平坦控制框图如图2 所示。图中，y、yref分别为平坦输出的实际值和期望输出值；Δy为y与yref之间的误差值；Δyref为误差值的期望值；uref，c为前馈控制量；uref，b为误差反馈补偿值；uref为最终的参考输入量。

图2 微分平坦系统控制框图Fig.2 Control block diagram of differential flatness system

2）M3C输入侧平坦控制器设计。

根据式（21），可得平坦控制的控制器前馈参考输入控制量为：

式中：Hd(s)、Hq(s)分别为d、q轴电流闭环传递函数。

这说明基于微分平坦理论设计的M3C的平坦控制器的输出电流能很好地跟踪参考给定值，不存在惯性环节，有很好的响应速度，且能实现独立解耦控制。

因此，可得M3C 输入侧控制框图见附录A 图A2（a），其中平坦控制的详细框图见附录A图A2（b）。

3 仿真分析

为了验证本文提出的M3C采用平坦控制策略的正确性及优越性，在MATLAB／Simulink平台上搭建了M3C 控制系统，并且模拟了输入侧频率变化及输出侧负载变化时的运行工况。M3C系统仿真参数如附录B表B1所示。

平坦控制参数KDFp变化对输入侧d轴电流的影响如图3所示。由图可见，KDFp=39时效果最好，系统到达稳定的时间最快且超调量小，因此选择KDFp=39。由于系统稳态误差较小，KDFi变化对系统波形的影响不大，故设置KDfi=86。

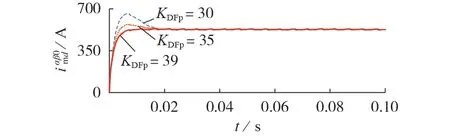
图3 KDFp对输入侧d轴电流的影响Fig.3 Influence of KDFp on input-side d-axis current

3.1 M3C的平坦控制策略与PI控制策略

图4为在PI控制、平坦控制策略下M3C输入侧三相电流在d轴上的电流；图5为M3C在平坦控制策略下的运行特性；图6为M3C在PI控制、平坦控制策略下的输入和输出波形。图5（a）中，uCar1、uCas1和uCat1分别为桥臂ar、桥臂as 和桥臂at 第1 个子模块的电容电压。可以看出，采用平坦控制策略时输入侧电流稳定速度更快、跟踪无静差、无超调，控制效果更好。

图4 正常工况下M3C输入侧d轴电流波形Fig.4 Waveform of input-side d-axis current of M3C under normal working condition

图5 正常工况下采用平坦控制策略时M3C的运行特性Fig.5 Operation characteristics of M3C with flatnessbased control strategy under normal working condition

图6 正常工况下M3C的输入和输出波形Fig.6 Input and output waveforms of M3C under normal working condition

3.2 M3C输入侧频率变化

0.1 s时，将输入侧频率由16.7 Hz提升至50 Hz；0.2 s 时，将输入侧频率由50 Hz 降低至16.7 Hz。此时，M3C 在PI 控制、平坦控制下的输入侧三相电流的d轴分量波形如图7所示；M3C在平坦控制下的输入和输出波形如图8所示。

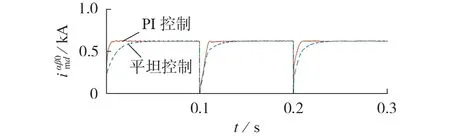
图7 输入侧频率变化时M3C输入侧d轴电流波形Fig.7 Waveform of input-side d-axis current of M3C when input-side frequency changes

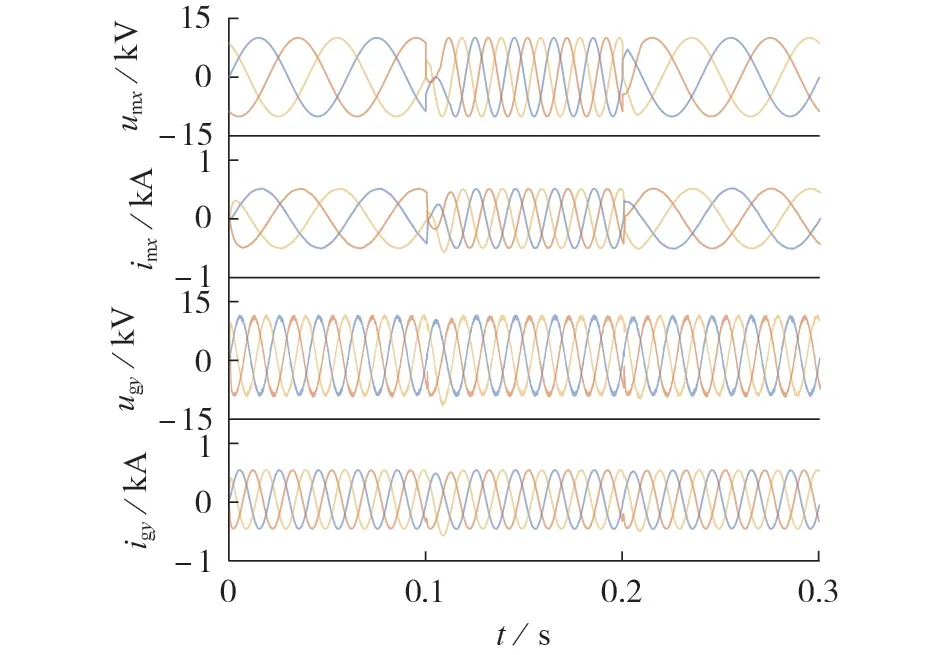
图8 输入侧频率变化时平坦控制策略下M3C输入和输出波形Fig.8 Input and output waveforms M3C with flatness-based control strategy when input-side frequency changes

进一步得到输入侧频率变化时输入侧三相电流波形分析与比较如表1 所示。由表可见，当输入侧频率变化时，采用平坦控制策略时的输入侧三相电流响应更快，谐波含量更低，控制效果更好。

表1 输入侧频率变化时输入侧电流波形分析与比较Table 1 Analysis and comparison of input-side current waveforms of M3C when input-side frequency changes

3.3 M3C输出侧负载变化

0.1 s 时，输出侧增加1 号负载（R1=30 Ω，L1=0.05 H）和2号负载（R2=20 Ω，L2=0.03 H）；0.2 s时，输出侧切除1 号负载。输入侧频率为16.7 Hz，输出侧频率为50 Hz。此时，M3C 在PI 控制、平坦控制下的输入侧三相电流的d轴分量波形如附录B 图B1 所示，M3C 在平坦控制下的输入和输出波形如附录B图B2所示。相应地，进一步得到输入侧频率变化时输入侧三相电流波形分析与比较如附录B 表B2 所示。由表可见，当输出侧负载变化时，采用平坦控制策略时的输入侧三相电流响应更快、谐波含量更低、控制效果更好。

4 结论

M3C输入侧的平坦控制策略以微分平坦理论为理论基础，以系统的大范围渐近稳定为控制目标。通过李雅普诺夫方法证明其稳定性，并推导出平坦控制策略。本文对PI 控制与平坦控制策略进行对比，通过理论分析、推导和仿真，验证了本文提出的平坦控制策略的有效性和正确性，且得出以下结论：

1）采用平坦控制策略时，输入侧三相电流的稳定速度更快，跟踪无静差，整体控制效果更好；

2）当输入侧频率变动、输出侧负载变动时，平坦控制策略均响应快速、无超调、动态性能高、对系统冲击量更小；

3）平坦控制策略控制简单，易于实现。

附录见本刊网络版（http：//www.epae.cn）。