深基坑组合型钢内支撑构件平面内稳定分析
李永华,肖云豪,章伟豪,揭一鸣
(南昌大学 建筑工程学院,江西 南昌 330031)
近几年来,一种组合型钢内支撑构件得到了广泛的应用。与混凝土内支撑相比,组合型钢内支撑构件可回收利用,减少了资源消耗,且施工过程噪声小,绿色环保。组合型钢内支撑构件是H型钢之间采用缀条或缀板相连,从而形成格构式支撑构件,水平面内抗弯刚度得到明显提高,在大型基坑中通常可以单向布置,大大方便了施工应用。在临近地铁或铁路的基坑施工过程中,组合型钢内支撑可以通过施加预应力来控制地铁隧道或铁路路基的变形,具有重要的工程意义。图1为组合型钢内支撑构件现场施工图,内支撑构件根据设计需要通常采用3肢及以上型钢进行组合,图2为组合型钢内支撑托架图,下承托架由立柱与横梁组成,立柱和横梁一般均采用H型钢,横梁支承于立柱牛腿上,两者之间通过高强螺栓进行连接。当地质情况较好时,立柱可直接插入地基土中,当地基土质较差时常设置素混凝土灌注桩作为立柱基础[1]。刘兴旺等[1]认为组合型钢内支撑构件承载力实际上是稳定性问题,包括水平面内和竖直平面内,且立柱对稳定性起关键作用。组合型钢内支撑构件稳定类似于具有多道弹性支撑杆的钢柱稳定问题[2-13],陈绍蕃[2]对轴向荷载作用下,具有2~4道弹性支撑杆钢柱的弹性临界荷载进行了分析,并在此基础上提出了具有多道弹性支撑杆钢柱临界荷载的拟合公式。本文采用能量法对10道及以下弹性支撑的钢柱弹性临界荷载进行分析,通过在公式中引入屈曲半波数及支撑道数作为变量,直接得出无量纲化的钢柱临界压力和无量纲化支撑刚度之间的通解,避免了文献[2]曲线拟合带来的误差,同时分析了剪切变形对多肢组合格构式型钢内支撑构件稳定的影响,便于工程应用。

图1 组合型钢内支撑构件现场施工图Fig.1 Construction diagram of assembly steel struts

图2 组合型钢内支撑构件托架Fig.2 Bracket of assembly steel struts
1 具有多道弹性撑杆的钢柱临界压力拟合公式
陈绍蕃[2]对具有多道弹性撑杆的钢柱无量纲化的临界压力和无量纲化的支撑刚度之间的关系进行拟合,得到统一的近似公式:
当Kl/N0≤3/j4时:

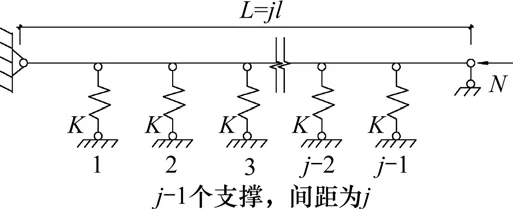
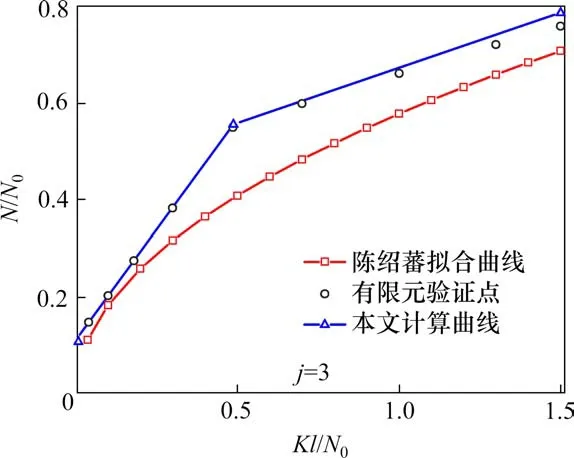
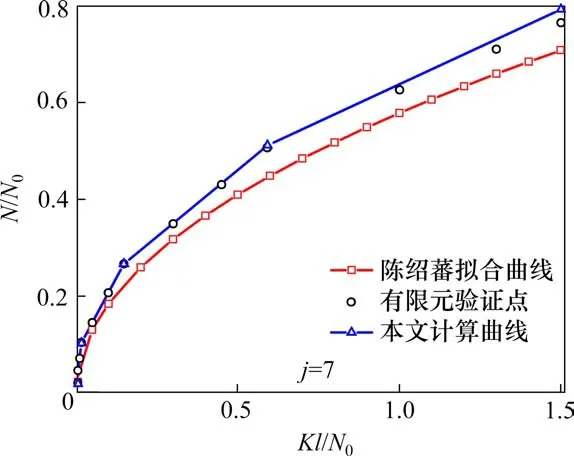
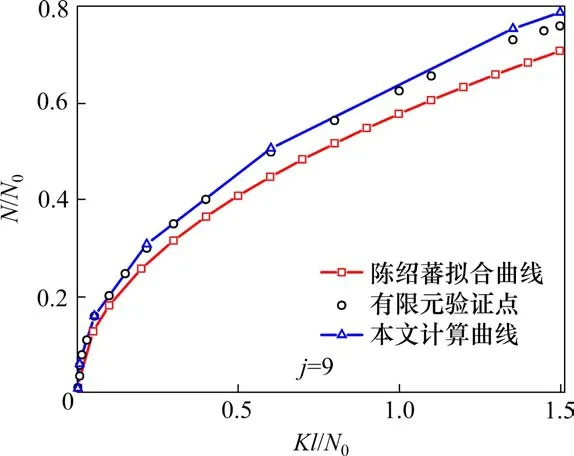
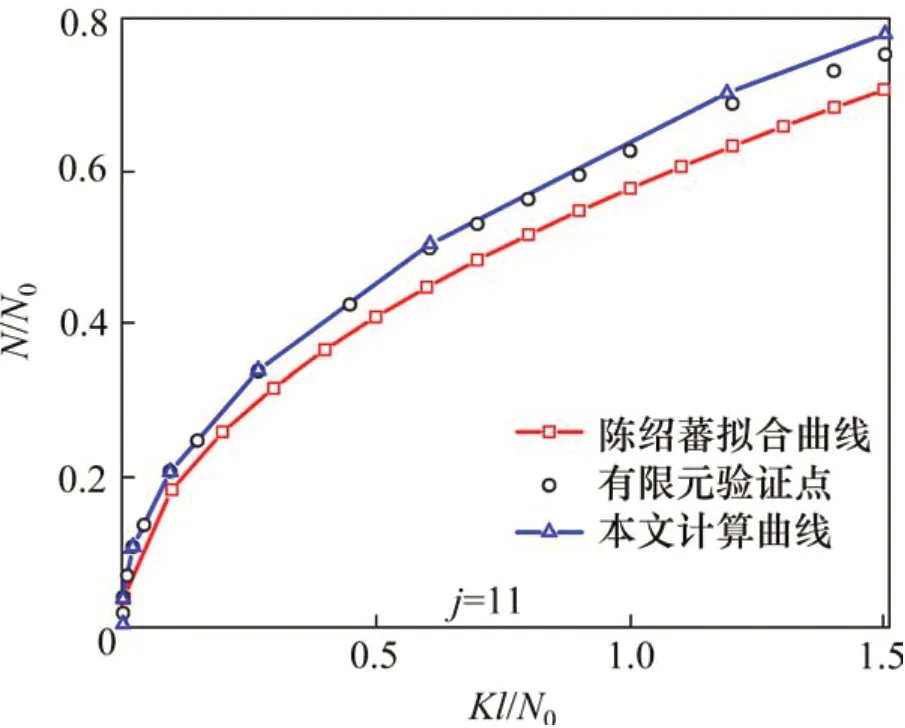
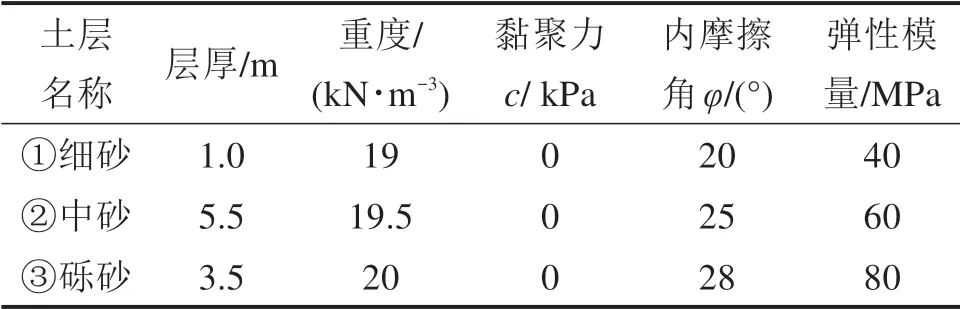
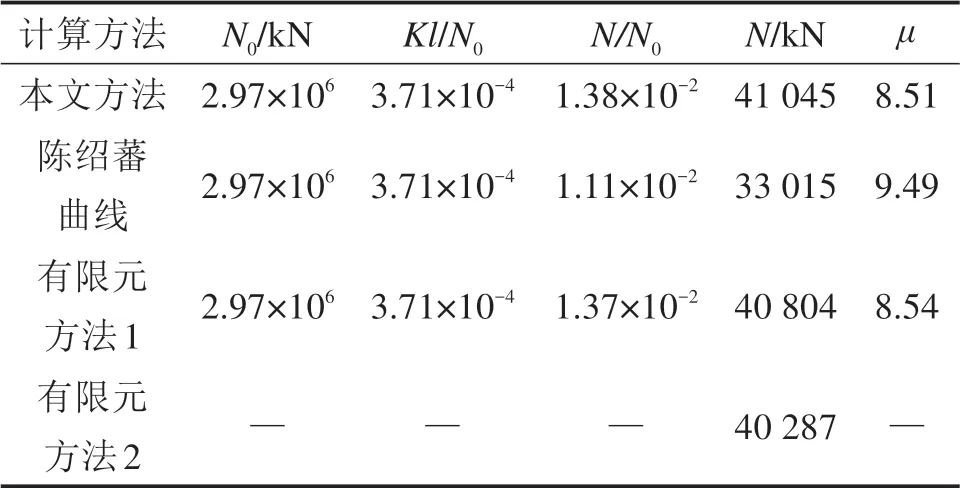
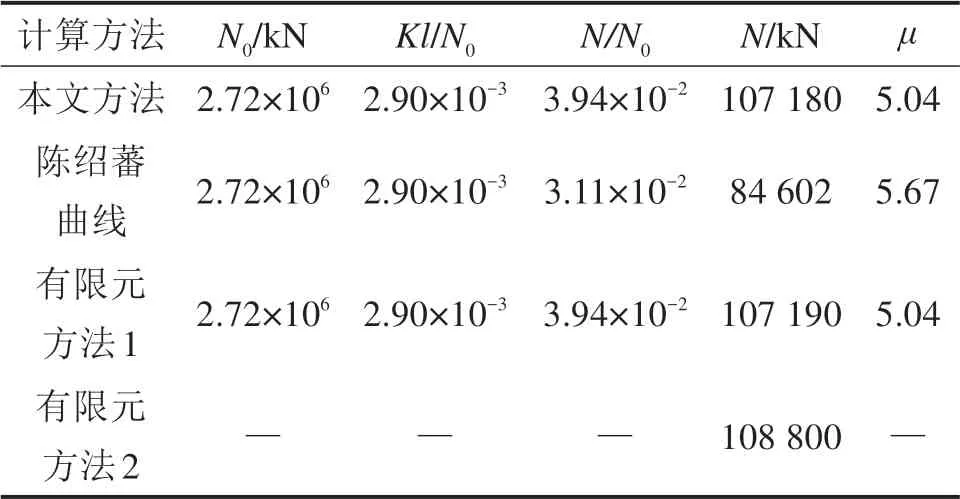
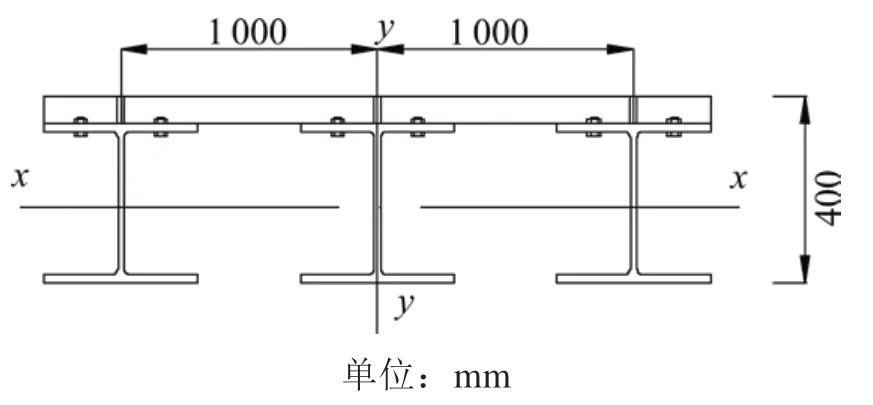
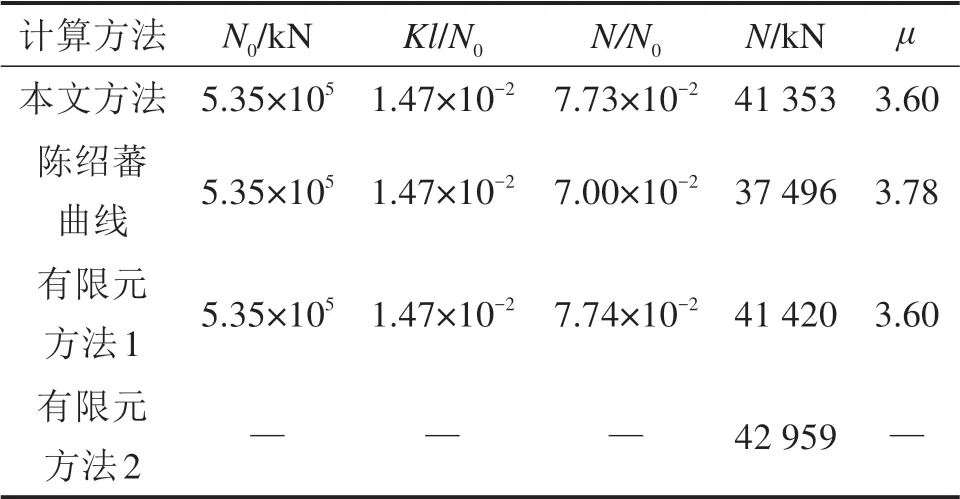
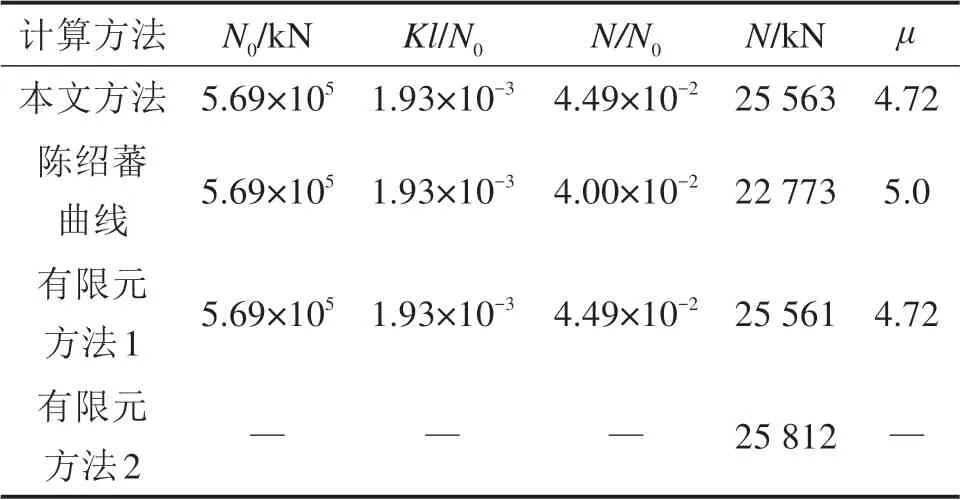
当3/j4 当1.5 当Kl/N0≥3.75时: 式中:N为具有多道弹性撑杆钢柱的弹性临界压力;N0为支撑间柱段的弹性临界压力,N0=π2EI/l2,l为柱段长度;K为弹性撑杆的刚度;j为柱的分段数,即弹性撑杆道数加1。 《预应力鱼腹式基坑钢支撑技术规程》[14]给出了组合型钢内支撑构件考虑托架作用时水平面内稳定分析时计算长度系数统一公式μ=(3N0/kl0)1/4,由于μ=,所以规程中的计算长度系数μ实际上是根据式(2)推导出来的,需强调的是,式(2)适用范围为无量纲化的支撑刚度Kl/N0位于3/j4 具有j-1个支撑的钢柱受轴向压力N作用,如图3所示,支撑间的长度均为l,钢柱总长度L=jl,钢柱的抗弯刚度为EI,弹性撑杆刚度为K,当屈曲半波数m=j时,这时全部撑杆均达到门槛刚度,门槛刚度为当撑杆达不到门槛刚度时,假设钢柱呈现m个半波屈曲,屈曲变形曲线为: 图3 j-1个支撑钢柱计算模型Fig.3 Calculation model of steel column with j-1 braces 式中:am为常数,m屈曲半波数,m=1,2,3,…,j-1。x表示沿柱轴向方向的坐标,正方向为从左至右。 y的一阶导函数和二阶导函数如下: 柱子的弯曲应变能力和弹性支座的应变能分别为: 式中:yi为第i个弹性支座的位移。 柱子的外力功为: 总势能为: 式中:NE为支撑杆刚度为0时钢柱的欧拉临界力,NE=π2EI/L2。 按势能驻值原理对am进行求导并令导函数等于0得到: 将式(12)进行整理,可得: 式中:N0为撑杆达到门槛刚度或者说撑杆起刚性支座作用时钢柱临界力,N0=π2EI/l2,进一步整理可推导出: 式(14)为钢柱发生m个半波屈曲时无量纲化的支撑刚度与无量纲化的临界压力之间的关系,比陈绍蕃拟合曲线还简单,但由于公式中引入了屈曲半波数m这个变量,故需对屈曲半波数m变化时的转折点进行求解。 当钢柱产生m+1个半波屈曲时,同理可得出: 式(15)为钢柱发生m+1个半波屈曲时钢柱的支撑刚度与临界力之间的关系。式(14)与式(15)可联立进行求解,得出由m个半波屈曲向m+1个半波屈曲转折时的无量纲化的支撑刚度与临界压力值如下: 具体应用时,操作步骤如下: 1)先根据弹性支撑的刚度K,支撑间距l及撑杆达到门槛刚度时临界力N0,计算无量纲化的支撑刚度Kl/N0,然后从m=1,2,3…开始,分别计算式(16)中的值; 2)如果当m=p时,无量纲化的支撑刚度Kl/N0满足则p即为与弹性支撑刚度对应的屈曲半波数; 3)m值确定后,可由式(14)直接计算出与支撑刚度相对应的无量纲化的临界力N/N0的值。 采用本文计算方法,分别对2,4,6,8,10道弹性撑杆作用下的钢柱临界压力采用式(14),式(15)进行计算,得出的无量纲化的支撑刚度Kl/N0与无量纲化的钢柱临界压力N/N0之间的关系,具体计算结果如图4~8所示。为便于对比分析,图中同时给出了陈绍蕃拟合曲线、有限元弹性特征值屈曲方法计算结果,由于本文研究仅限于Kl/N0≤1.5这一范围应用,故只给出该范围的计算结果。 图4 2道弹性支撑时的弹性临界荷载与支撑刚度的关系Fig.4 Relationship between the critical load and the brace stiffness of two elastic braces 图5 4道弹性支撑时的弹性临界荷载与支撑刚度的关系Fig.5 Relationship between the critical load and the brace stiffness of four elastic braces 图6 6道弹性支撑时的弹性临界荷载与支撑刚度的关系Fig.6 Relationship between the critical load and the brace stiffness of six elastic braces 图7 8道弹性支撑时的弹性临界荷载与支撑刚度的关系Fig.7 Relationship between the critical load and the brace stiffness of eight elastic braces 图8 10道弹性支撑时的弹性临界荷载与支撑刚度的关系Fig.8 Relationship between the critical load and the brace stiffness of ten elastic braces 有限元验证时,采用图3所示钢柱模型,钢柱采用beam3单元进行模拟,钢柱截面面积为0.109 4 m2,截面惯性矩为0.219 m4,钢柱支撑间距为12 m。当屈曲半波数确定后,式(14)和式(15)均为线性方程,2条直线的交点就是图(4)~(8)中的折线转折点,所有转折点均在图上采用三角形进行标注,转折点之间采用直线相连,所以没用三角形进行标注。 从图4~8对比分析可以看出,本文采用的方法与ANSYS有限元曲线验证点很接近,计算精度比陈绍蕃拟合曲线有一定的提高,陈绍蕃拟合曲线N/N0误差总体上呈现随支撑刚度增大而增大趋势。 从图1~2可以看出,组合型钢内支撑构件水平面内的稳定为绕虚轴的稳定,文献[15]给出了平行双肢格构柱考虑剪切变形影响的计算公式,但对于平行三肢或以上的格构柱剪切变形影响公式还未见相关文献进行研究,本文以三肢缀板式组合型钢内支撑构为例,进行剪切变形影响系数的推导。 三肢组合型钢内支撑构件缀板与肢件的连接同样视为刚接,整个构件相当于一个多跨的多层刚架体系,体系发生剪切变形时,缀板与肢段均呈S形弯曲(图9),柱肢反弯点可近似取在肢段的中点。图9(a)为三肢格构柱整体计算模型,图9(b)为肢件变形详图,图9(c)为缀板变形详图。 图9 三肢格构柱计算模型Fig.9 Three-limbed lattice column calculation model 图9(b)肢件在A结点和反弯点间的一段,可视为一悬臂梁,在单位水平剪力作用下的线位移为: 式中:Izh表示单根肢件绕平行于虚轴的形心轴的惯性矩;b为相邻缀板之间的距离。 图9(c)为连续缀板计算模型图,由于A,B,C3点弯矩相等,对该超静定结构采用力法进行求解后可得出: 式中:Ib表示缀板对其形心轴的惯性矩,由式(18)和式(19)可得单位剪力作用下的剪切角γ: 由结构力学相关知识可知,考虑剪切变形后的弹性临界荷载为[11,15]: 式中:N是不考虑剪切变形时构件弹性临界荷载;Ns为考虑剪切变形时构件弹性临界荷载。 将式(20)代入式(21)中,可得: 假定考虑剪切变形后的弹性临界荷载采用下式进行表示: 式中:Is就是考虑剪切变形修正后的整体截面惯性矩,综合式(22)与式(23)可得出: 同理,可推导出五肢缀板式格构构件考虑剪切变形修正后的截面惯性矩,由于相对于肢件的弯曲变形产生的剪切角,缀板弯曲角θ的影响较小,通常可略去[15],简化后的五肢格构柱考虑剪切变形影响后的截面惯性矩为: 1号组合型钢内支撑构件总长度120 m,组合型钢内支撑构件截面如图10所示,由5肢型钢进行组合,单肢型钢为HW400×400×13×21,缀板型号为-4 350 mm×750 mm×12 mm,型钢肢件中心间距1 m,缀板中心间距2 m,内支撑构件下面设置了9道由立柱与横梁组成的托架进行支托,托架沿内支撑构件长度方向等间距布置,间距l=12 m,内支撑构件的水平面内稳定问题可以抽象为9道弹性支撑杆作用下的钢立柱稳定问题(j=10),弹性撑杆的刚度等于托架水平抗侧移刚度。 图10 1号组合型钢内支撑构件截面Fig.10 No.1 assembly steel struts section 托架立柱采用H350×350×12×19型钢,横梁采用H300×300×10×15型钢,横梁跨度6 m,立柱总长度16 m,基坑上部8 m,嵌入基坑底部8 m,基坑坑底以下土体分别为细砂、中砂及砾砂,土层信息如表1所示。 表1 土层信息Table 1 Soil information 考虑到PLAXIS有限元软件在处理立柱与土体接触比较方便,本文采用PLAXIS有限元软件来计算托架的水平抗侧刚度,托架立柱弹性嵌固于土体中,弹性嵌固的立柱可采用m值法进行计算[16],也可采用有限元方法计算,m值计算时嵌固程度主要由土的黏聚力c值及内摩擦角ϕ值确定,有限元计算时嵌固程度主要由土体弹性模量确定,当托架为排架时,计算得出抗侧移刚度K=180 kN/m,当托架为刚架时,抗侧移刚度K=1 314 kN/m。考虑到托架的初始偏心以及初始几何缺陷,设计时将托架抗侧移刚度均降低一半[11],即分别采用K=90 kN/m和K=657 kN/m用于分析。 共采用了4种方法进行计算,一种是本文方法,另一种为陈绍蕃曲线拟合法,这2种方法计算过程中均采用式(25)计算了剪切变形对组合型钢截面惯性矩的影响;另外2种方法均为采用ANSYS有限元软件进行弹性特征值屈曲分析,有限元方法1将格构式构件等效成实腹杆模型,惯性矩采用剪切变形修正后的组合型钢截面惯性矩,有限元方法2直接采用格构式模型建模,即对组合型钢分肢及缀板逐一采用Beam3单元进行建模。 表2和表3分别给出了托架为排架、刚架2种工况下,4种方法计算得出的组合型钢内支撑构件水平面内的无量纲化支撑刚度、无量纲化的临界压力及计算长度系数。 表2 托架为排架时,1号内支撑临界荷载及计算长度系数Table 2 Critical load and effective length factor of No.1 strut supported by bent 表3 托架为刚架时,1号内支撑临界荷载及计算长度系数Table 3 Critical load and effective length factor of No.1 strut supported by portal frame 从表2和表3可以看出,本文方法与有限元计算方法1很接近,精度比陈绍蕃曲线有一定的提高,另外本文计算方法与有限元格构式模型计算结果也很接近,说明本文剪切变形影响系数的推导是合理的。不考虑托架的贡献时,1号组合型钢内支撑构件计算长度系数应为10,从表2和表3可以看出,当托架为排架时,计算长度系数降低约15%,但当托架为刚架时,计算长度系数下降约50%。 2号组合型钢内支撑构件总长度60 m,内支撑构件截面如图11所示,由3肢型钢进行组合,单肢型钢截面同上,缀板型号为-2 350 mm×750 mm×12 mm,型钢肢件中心间距1 m,缀板中心间距2 m。 图11 2号型钢组合内支撑构件截面Fig.11 No.2 assembly steel strut section 内支撑构件下面共设置了4道托架进行支托,托架沿内支撑构件长度方向等间距布置,间距l=12 m。内支撑构件的水平面内稳定问题可以抽象为4道弹性支撑杆作用下的立柱稳定问题(j=5),弹性支撑杆的刚度等于托架的水平抗侧移刚度。 采用前述方法可得出2号内支撑构件水平面内无量纲化支撑刚度、无量纲化的临界压力及计算长度系数,详见表4和表5。 表5 托架为刚架时,2号内支撑临界荷载及计算长度系数Table 5 Critical load and effective length factor of No.2 strut supported by portal frame 不考虑托架贡献时,2号内支撑构件计算长度系数应为5,当托架为排架时,组合型钢内支撑构件的计算长度系数降低至4.72,计算长度系数下降约5.6%,当托架为刚架时,组合型钢内支撑构件的计算长度系数降低至3.6,计算长度系数下降约28%。 需说明的是,当托架为排架时,表4中无量纲化的支撑刚度Kl/N0=1.93×10-3,本算例中j=5,故3/j4=4.8×10-3,此时,Kl/N0≤3/j4,刚好处于陈绍蕃拟合曲线第一段,但如果按现行《预应力鱼腹式基坑钢支撑技术标准》[14]中的计算长度系数公式μ=(3N0/kl0)1/4来进行计算,得出的计算长度系数μ=6.3,明显失真。 表4 托架为排架时,2号内支撑临界荷载及计算长度系数Table 4 Critical load and effective length factor of No.2 strut supported by bent 1)通过引入屈曲半波数及支撑道数2个变量,推导了对应不同屈曲半波数的弹性临界荷载与支撑杆刚度之间的通解,在此基础上进一步得出了不同屈曲半波数转折点对应的支撑刚度,与传统曲线拟合方法相比,本文方法计算结果精度有一定的提高。 2)通过对60 m和120 m长度的2个组合型钢内支撑构件基坑工程算例可以看出:考虑托架作用时,当托架为排架形式,120 m长度内支撑构件计算长度系数可降低15%,60 m长度内支撑构件计算长度系数可降低5.6%;当托架采用刚架形式时,120 m长度内支撑构件计算长度系数可降低50%,60 m长度内支撑构件计算长度系数可降低28%。
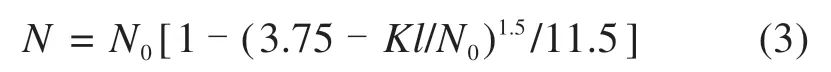

2 具有多道弹性撑杆钢柱临界压力通解
2.1 能量法理论求解
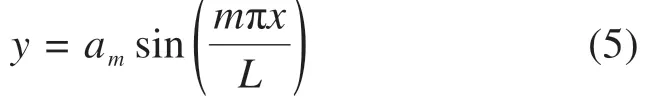

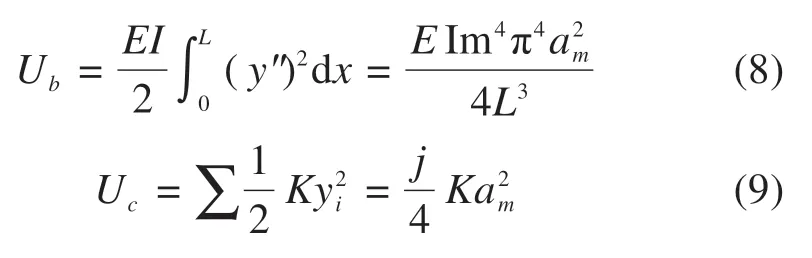
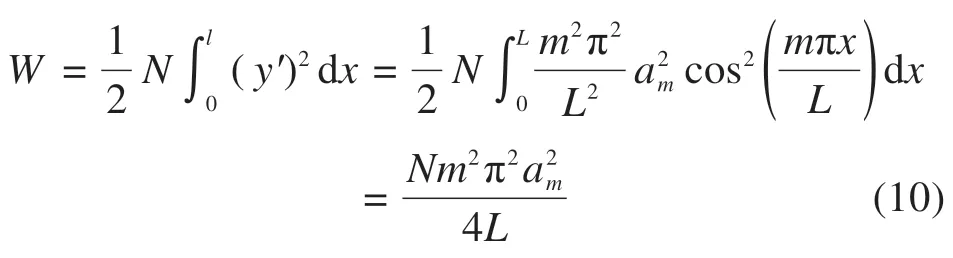

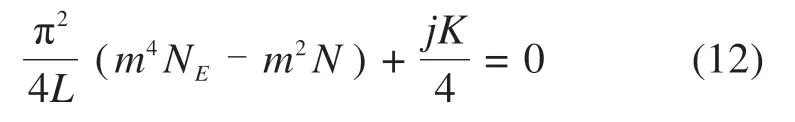


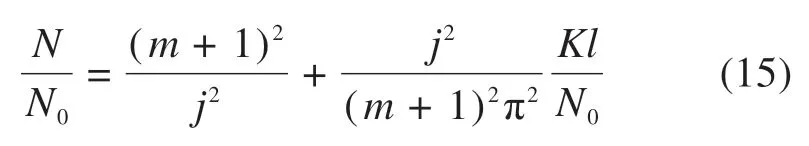
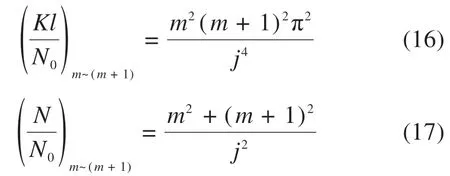
2.2 应用步骤
2.3 计算结果对比分析

3 剪切变形对组合型钢内支撑影响


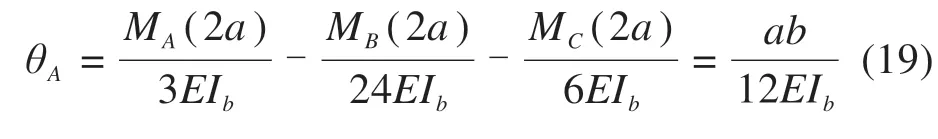






4 工程算例
4.1 1号型钢内支撑

4.2 2号型钢内支撑
5 结论

