基于Python优化的任意钢-混组合截面应力与承载力分析研究

阴文蔚

(中铁第五勘察设计院集团有限公司，北京 102600）

随着土木工程结构的创新与发展，工程中经常会采用由不同材料及非常规几何形状截面组合而成的复杂截面。该截面在外部作用下的应力及极限承载能力的计算已超出了设计规范计算公式的范围。目前，对任意截面应力及极限承载力计算分析主要有3种方法：强度叠加法、数值积分法以及纤维单元法[1]。强度叠加法是利用规范现有的钢筋混凝土构件及钢构件的承载能力计算公式，根据某种原则进行叠加，叠加结果作为型钢混凝土构件承载力的近似[2]。这种方法理论基础是完善的，但由于理论本身特点，对具有复杂几何外形的组合截面，不易求得真实的极限承载力，并且简化方法偏于保守[3]。数值积分法是对截面进行分解，推导出各分部的积分方程，通过数值逼近进行近似计算。数值积分法计算可以在一定精度条件下求解，但面临任意截面时，其公式较多，计算过程较为复杂，增加了编程的难度。RODRIGUEZ等[4]使用高斯积分方法求解外荷载与内力的平衡，但对加载轴的原点位置比较敏感，会有不收敛的情况出现。FAFITIS[5]使用格林定理对多边形截面的应力进行积分，但该方法每一步都需要确定不同子区域。纤维单元法基于平截面假定并认为黏结滑移造成的影响较小，将截面各部分划分成细小网格，认为每一网格内应力应变相同，当网格划分足够细时，便可达到所需精度。BONET等[6]基于上述假定，开发了一种迭代的计算机方法，利用纤维单元方法对包裹的复合材料柱进行双轴弯曲计算，得到了数值结果。CHEN等[7]提出使用塑性中心作为荷载加载轴的原点，并采用同样的迭代方法开发出一种计算机方法，通过对混凝土受压区进行积分求得混凝土部分的内力。SFAKIANAKIS[8]提出了一种以计算机图形学为计算工具的替代纤维模型，用于计算截面区域的正应力，并研究了任意形状钢筋混凝土截面在轴力作用下双向弯曲的破坏机理。上述计算方法中对任意组合截面的网格需要人工划分，使用时很不方便，网格划分精度不宜随意控制。我国《混凝土结构设计规2015年版》(GB 50010—2010)中给出计算机计算钢筋混凝土构件正截面承载力的方法，但是需要在混凝土受压区顶点做一条与中和轴平行的直线作为初始中和轴然后再进行迭代计算，此外，其对于环形及圆形构件的计算较为复杂，并且存在一定误差[9]。综上，数值积分法在大轴力下难收敛，尤其对于圆形截面的计算困难更为明显。基于纤维单元法的截面应力求解多采用计算机迭代求解，利用拟牛顿法迭代求解时面临不收敛的问题，虽然可以使用塑性中心作为荷载加载轴的原点局部解决此问题，但不能保证计算收敛。针对上述情况，本文基于平截面假定推导出任意组合截面的中心轴位置计算公式及截面内力计算公式，利用目前流行的Python编程语言及其强大的功能库进行有限元网格划分及优化模型求解，准确、快速、高效地完成了对任意组合截面在轴力及双弯矩作用下的截面应力及极限承载力的计算。

1 计算方法

1.1 基本假定

本文计算采用如下基本假定：

1)计算截面满足平截面假定，由此，截面上任一点处的应变都与其到中性轴的距离成正比。

2)每个网格区域内的应力应变均相同，且可以由网格形心处应力应变代表。

3)不考虑组成截面的各材料间的黏结滑移的影响。

4)截面任意一根纤维应变值超过规定极限应变则认为截面破坏。

5)规定截面上的应力应变与轴向力受拉为正，受压为负。作用在截面上的弯矩方向满足右手定则，其矢量方向沿坐标轴正向为正。

1.2 计算公式推导

任意三角形网格位置如图1所示，在xoy坐标系下，中性轴位置由3个参数a，b，c来确定，则中性轴的一般方程为：

图1 任意三角形网格位置Fig.1 Position of arbitrary triangle mesh

截面上任意一个三角形网格形心到中性轴的距离(具有正负)可以由式(2)计算：

其中：xic和yic分别为当前三角形网格形心的x和y坐标，由三角形顶点坐标求得，为：

在中性轴假定已知的情况下，若要求得截面上某网格形心处的应变，还需一个参数，即截面在外荷载作用下绕中性轴的转角θ，则该点处的应变可以由式(4)计算：

此处需要注意，θ是具有正负的。本文方法约定：当截面绕中性轴发生转角θ时，使得xoy坐标系下d>0的区域受压的θ为负，反之为正，如图2所示。如此可以保证根据式(4)求得的应变无需通过分类讨论或者添加绝对值即可满足基本假定e，有效地避免了优化过程中目标函数出现不连续可导的情况，增加了计算稳定性。

图2 截面转角示意图Fig.2 Diagram of section angle

网格形心处应力σ可根据对应材料的本构关系进行计算。

根据基本假定b，各网格区域内应力应变与其形心处应力应变均相同，则各网格区域的内力可以由式(5)计算：

Ai为当前三角形网格的面积，可以由网格顶点坐标计算得到，见式(6)：

通过对截面上的应力进行积分，即可得到外荷载作用下截面的内力。当截面进行网格划分并且网格精度足够时，截面内力可以用各网格内力之和近似表示，如式(7)所示：

将式(2)～(6)代入式(7)，即可得到截面内力分别关于自变量a，b，c，θ的表达式，由于前文的正负号规定，此处计算得到的M′y与外荷载My符号相反，其余截面内力与外荷载符号相同，则目标函数Q应按照式(8)表示为：

对目标函数Q进行优化，求其最小值，当Q函数值小于规定精度值时，即认为优化成功，此时使Q取得最小值的a，b，c，θ即为最终解。根据式(1)～(4)即可得到正确的中性轴位与网格应变，最后再根据材料的本构关系求得其对应的应力大小。

2 程序设计

2.1 网格划分

网格划分是建立有限元模型的一个重要环节，所划分的网格形式对计算精度和计算规模将产生直接影响，网格划分时应主要考虑如下原则：

1)网格数量：网格数量将直接影响计算结果的精度和计算规模的大小。数量增加，计算精度会有所提高，但同时计算规模也会增加，所以在确定网格数量时应权衡2个因数综合考虑。如果仅仅是计算结构的变形，网格数量可以少一些。如果需要计算应力，则在精度要求相同的情况下应取相对较多的网格。

2)网格疏密：在计算数据变化梯度较大的部位如应力集中处，为了较好地反映数据变化规律，需要采用比较密集的网格。而在计算数据变化梯度较小的部位，为减小模型规模，则应划分相对稀疏的网格。

3)单元阶次：许多单元都具有线性、二次和三次等形式，其中二次和三次形式的单元称为高阶单元。选用高阶单元可提高计算精度，当结构形状不规则、应力分布或变形很复杂时可以选用高阶单元。

4)网格质量：网格质量是指网格几何形状的合理性。质量好坏将影响计算精度，质量太差的网格甚至会中止计算。网格各边或各个内角相差不大、网格面不过分扭曲、边节点位于边界等分点附近的网格质量较好。在重点研究的结构关键部位，应保证划分高质量网格，而在结构次要部位，网格质量可适当降低。

5)位移协调性：位移协调是指单元上的力和力矩能够通过节点传递给相邻单元。为保证位移协调，一个单元的节点必须同时也是相邻单元的节点，而不应是内点或边界点。相邻单元的共有节点具有相同的自由度性质。

2.2 Python功能库

Python是一种功能非常强大的编程语言，是一种简单有效、面向对象的编程方法[10]。它具有高效的高级数据结构、且易于学习和高度可扩展[11]。基于其开源的特性，Python除了具有完善的标准库外，还有庞大的第三方库。

Python中的Meshpy库提供了高质量的三角形和四面体网格生成功能。这种类型的网格主要用于有限元模拟程序，也有许多其他的应用，比如从计算机图形学到机器人技术的各个领域均有涉及。MeshPy为3个较出名的网格生成器(Triangle、TetGen、gmsh)提供了Python接口，能够实现任意截面的三角网格划分。Triangle程序专门用于创建二维有限元网格，所划分的三角网格整体均匀且具有唯一性，保证多次计算前后结果相同。任意截面及其划分网格后结果如图3所示，图中圆形区域代表孔洞，五角星部分和其余区域分别代表由不同材料组成的截面[12]。

图3 任意截面网格划分示意图Fig.3 Meshing diagram of arbitrary cross section

Python中的SciPy库是构成SciPy堆栈的核心包之一。它提供了许多高效的数值例程，如数值积分例程、插值程序、优化程序、线性代数程序和统计程序。Scipy库所含Optimize软件包提供了多种常用的优化算法，如minimize，basinhopping，differential_evolution和minimize_scalar等，能够 快速实现多种优化函数的求解。minimize函数用来求解一个或多个变量的标量函数的最小化，它含有多种求解方法，如BFGS，Newton-CG和SLSQP，可根据优化函数特性进行选择，SLSQP方法是序列二次规划法。basinhopping是一种两阶段方法，它将全局步进算法与每一步的局部最小化相结合，旨在模拟原子团簇能量最小化的自然过程。Basinhopping方法求解速度较慢，但是收敛性极好，minimize求解速度快，但会在个别情况下不收敛。对于复杂截面，优化计算过程中单独采用SLSQP方法有时会遇到计算不稳定的问题，结合basinhopping便能够保证计算结果正确[13]。

2.3 程序编制

2.3.1 程序算法

本文算法基于Python中的Meshpy库及Scipy库实现任意组合截面的网格划分及优化求解。根据1.2节所述，将任意形状的截面自动划分成网格，以中性轴参数及截面转角为变量，通过待定的中性轴求得截面内力，并将内、外力差值的平方和作为目标函数，通过对目标函数Q(a,b,c,θ)进行优化，得到一组最优解，再由这组最优解求解其在外荷载作用下截面的应力应变以及中性轴具体位置。若外荷载超出其截面的极限承载力时，则程序将求出截面的极限承载力与其对应的应力和应变值。其中：网格三角形顶点坐标由Meshpy库中Triangle网格生成器提供；优化求解采用Scipy库中minimize和basinhopping2种优化算法。basinhopping方法求解速度较慢，但是收敛性极好，minimize求解速度快，但会在个别情况下不收敛，因此本程序将二者结合起来，当minimize不收敛且满足一定条件时，选用basinhopping方法，使得程序求解更加高效。若程序转为求解截面极限承载力，则本程序将通过二分法查找其极限承载力，优化方法依然是minimize与basinhopping相结合的方法。

2.3.2 程序流程

程序流程图如图4所示。对于给定荷载，本程序采用逐级加载的方式来求解最终的应力应变或者其极限承载力。在将荷载分为n级后，首先假设a，b，c，θ的初值，然后施加第1级荷载，按照1.2节所述求得目标函数Q，对其进行优化，可以求得在此荷载下的a，b，c，θ的正确值。然后再将此次的结果作为计算下一级荷载时所需假设的参数的初值，进行求解。如此可以大幅提高求解效率。以此类推，即可最终求得在给定荷载下的截面应力应变。

图4 截面应力及承载力计算程序流程图Fig.4 Flowchart for calculation of section stress and load-carrying capacity

若在逐级加载的过程中，根据基本假定d，经判别，发现在第i级荷载作用下，截面某种材料超过预先规定的极限应变值(ε<εcu)或者经2种优化方法计算后均不收敛(Q>tol，即目标函数值大于规定精度)，则停止逐级加载，并在第i-1到i级荷载之间通过二分法寻找截面的极限承载力。在二分法寻找过程中，对于每一组加载力，依旧使用图4中第4～7步进行计算，直至计算结果同时满足：材料应变小于极限应变(ε<εcu)、目标函数值小于规定精度(Q>tol)、二分法搜寻区间小于规定大小(dMx≤dMxmin，dMy≤dMymin)。此时认为，二分法寻找成功，当前作用于截面的荷载即为其极限承载力。

3 算例

本方法既能用于线弹性应力计算也能用于材料非线性极限承载力计算。为了验证本文方法及程序的准确性和效率，给出3个算例，并与原文献中的计算结果进行比较。

3.1 算例1

如图5所示，算例1为童森林[14]所研究的一个算例。算例基于线弹性本构，应力应变成正比，并且不考虑混凝土受拉。xoy坐标原点取圆端形截面形心，截面尺寸b=2.1 m，R=1.15 m，其所承受外荷载为：N=-5 301 kN，Mx=1 960 kN·m，My=3 714 kN·m。

图5 圆端形截面Fig.5 Diagram of round-ended section

经计算，混凝土最大压应力为1 808 kPa，原算例混凝土最大压应力为1 805 kPa，相对误差δ=0.16%。计算结果表明，基于线弹性本构时，算例计算高效稳定且具有较好的精度。

3.2 算例2

本算例参考自CHEN等[7]。截面组成及尺寸见图6(a)。本截面由圆形空洞、工字型钢、钢筋及混凝土组成，混凝土内布置有15根直径12 mm的钢筋。

图6 型钢混凝土组合截面Fig.6 Diagram of composite section

钢筋与工字型钢均采用理想弹塑性本构。其中fs=355 N/mm2，fy=460 N/mm2，γs=1.1,γy=1.15。不考虑混凝土受拉，受压区应力应变关系由一条抛物线和水平段组成，并且不考虑钢筋对混凝土的约束作用。混凝土应力应变关系见式9(a)和9(b)。

式(9)中：fcc=0.85fck/γc，fck=30 N/mm2，γc=1.5，ε0=0.002，εcu=0.0035。

CHEN等[7]算例中为了使计算收敛，将外荷载作用于截面塑性中心(以下简称塑心)，为便于同原结果对比，本算例中将荷载也移动至塑心，并取塑心为xoy坐标原点。塑心o相对于截面左下角位置变化为Δx=292.2 mm，Δy=281.5 mm。作用于塑心的外荷载为N=-4 120.0 kN，Mx=209.78 kN·m，My=-863.964 kN·m，则弯矩方向为αm=arctg(My/Mx)=103.7°。

计算结果表明，在此组外荷载作用下，截面达到极限承载力，弯矩方向的极限承载合力矩为744.59 kN·m，原文结果为744.2 kN·m，相对误差δ=0.05%。提高钢筋直径至17.8 mm，本文程序计算的截面极限承载合力矩为892.76 kN·m，原文承载力为888.8 kN·m，相对误差δ=0.44%。

仍以截面塑心为坐标原点，在给定的轴向力(N=-4 120.0 kN)和钢筋直径时(ϕ=18 mm)，该组合截面的Mx-My相互作用曲线通过外加循环加载很容易得到。如图7所示，图中点所标记的数值为CHEN等[10]的各方向极限承载力，曲线为根据本文程序计算的各方向极限承载力经过拟合得到，二者接近重合，数据表明，在非线性应力应变关系下，复杂组合截面计算稳定且具有较高的精度。

图7 Mx-My曲线Fig.7 Mx-My interaction curve

3.3 算例3

本算例参考《钢-混凝土组合结构》例7-1[15]，截面组成及尺寸见图8(a)。本截面出自某组合楼盖体系中的简支组合梁横截面，截面上部为混凝土板横截面，厚度为90 mm，下部为工字钢梁横截面。混凝土强度等级C30，不考虑受拉，其应力应变曲线具体表达式如下。

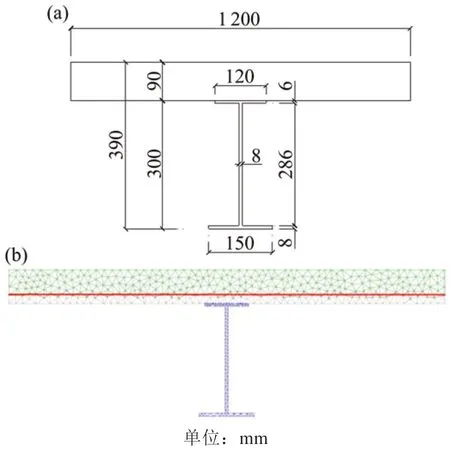
图8 组合梁截面Fig.8 Diagram of composite beam section

当x≤1时：

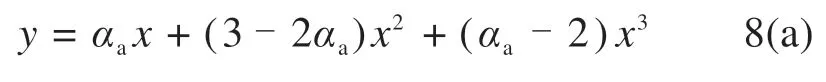
当x>1时：

式中：为混凝土单轴抗压强度设计值，取为14.3 N/mm2；εc为峰值压应变，取为1.64×10-3；αa取为1. 03；αd取为2.36。

钢材为Q235，屈服强度设计值为215 N/mm2，弹性模量为2.06×105N/mm2，其本构使用理想弹塑性模型。

原文计算原理与文献[15]中相同，是通过假设该截面各部分完全进入塑性状态来进行简化，从而求得截面极限承载力为207.6 kN·m，塑性中和轴位于混凝土板内，距截面顶部52.7 mm。如图8(b)所示，本文计算的该组合截面极限承载力为204.75 kN·m，中性轴位于混凝土板内，距截面顶部64.8 mm，承载力相对误差为δ=1.3%。与原文算例相比，本程序计算得到的中性轴位置较低，这是由于在原算例中假设全截面进入塑性状态，相较于实际情况，受压区高度减小，中性轴会有所上移。

计算结果表明，本方法在计算组合截面承载力时具有较高的准确性，同时也表明《组合结构设计规范》(JGJ 138—2016)[16]的简化算法误差较小，且简单可行。

以上算例中，网格数量可通过控制每个三角形的面积进行调整，经试算，当面积控制在0.000 5 m2以下时计算精度完全达到要求。

4 结论

1)基于Python框架Meshpy库高质量的三角形和四面体网格生成功能，使用Triangle网格生成器对组合截面进行自适应三角网格划分，使得算法能适用于任意形状、任意材料的组合截面。

2)基于Python框架的优化库，以中性轴参数及截面转角为变量，通过待定的中性轴求得截面内力，并将内、外力差值的平方和作为目标函数，结合minimize和Basinhopping 2种优化方法各自的优点，将2种方法混合使用进行优化模型求解，使得优化求解完全自动化，克服了其他方法收敛困难且不稳定的缺点，实现了对任意组合截面在轴力及双弯矩作用下的截面应力及极限承载力的计算。

3)本方法可以计算由任意多边形曲线构成的复杂截面，可以使用多种材料，同时也可以自行定义材料本构关系并且考虑材料非线性，可应用于任意组合截面的线、弹性应力计算及非线性弹塑性极限承载力计算分析。

4)经与文献中的经典算例对比分析，结果表明本文所述组合截面应力与极限承载力的计算分析方法计算速度快、收敛稳定且精度高，具有极强的实用性。