线性无量纲化方法比较研究
詹 敏,廖志高,徐玖平
(1.广西科技大学 管理学院,广西 柳州 545006;2.四川大学 商学院,四川 成都 610064)
【统计理论与方法】
线性无量纲化方法比较研究
詹 敏1,2,廖志高1,徐玖平2
(1.广西科技大学 管理学院,广西 柳州 545006;2.四川大学 商学院,四川 成都 610064)
根据线性无量纲化方法函数构成所使用的中心点值和值域指标以及其斜率和截距的表达式,对8种线性无量纲化方法进行分析,从不同的角度再次论证不同线性无量纲化方法所满足的性质定理,并进行了理论论证。同时,通过对线性无量纲化方法的分类比较,结合相关性质定理提出了多种线性无量纲化方法,并说明了其相关性质,具有一定的科学性。同时还分析了在对多指标数据进行综合评价的过程中只采用一种线性无量纲化方法的不足,提出了采用多种无量纲化方法的设想的理论可行性,并用案例进行了实证分析,表明其存在一定的合理性。
斜率;截距;中心点值;值域
一、引 言
在多指标综合评价的过程中,经常会遇到由于各个指标之间的单位和量级等不同而无法直接评价的问题,为了尽可能避免其带来的不利影响,客观反映被评价对象的真实水平,有必要对被评价对象原始指标数据作无量纲化处理[1]16-23[2-5]。指标数据的无量纲化,也叫做指标数据的标准化、规范化,它是通过数学变换来消除原始指标量纲影响的方法。对所有的评价指标原始数据进行无量纲化处理的过程通常包含三个方面的内容:同度量、同方向、同基准(包括同值域、同中心值或同某一端点值等)。同度量主要是将同一指标的原始数据单位统一;同方向是将逆向指标正向化,以及对区间指标、居中指标的正向化处理。同基准则是通过某一类型变换函数将不同指标的正向化数据转化为某一函数值,以便不同指标间进行相应的集结与比较。本文讨论的线性无量纲化方法主要是指确定同基准所采用的变换函数的方法。
现有的无量纲化方法主要分为两类:线性无量纲化方法和非线性无量纲化方法。线性无量纲化方法一般包括:标准化处理法、极值处理法、线性比例法、归一化处理法、向量规范法以及功效系数法等,其特点是无量纲化变换均为线性,线性变换函数的计算都运用了某些统计指标,如最大值、最小值、均值、方差等。还有一种较特殊的为基于奖优罚劣的线性无量纲化方法,其线性变换函数将大于平均值的数为正,小于平均值的数为负,由于弥补了只奖不罚的不足,并且评价结果识别性更高,有一定的优越性[6-7]。目前关于线性无量纲化方法的研究比较丰富。如郭亚军、易平涛指出,一个理想的线性无量纲化方法一般会满足单调性、差异比不变性、平移无关性、缩放无关性、区间稳定性以及总量恒定性这,且证明不存在线性无量纲化方法使得“区间稳定性”及“总量恒定性”两个性质同时成立,并推论出同时满足上述六条理想无量纲化方法不存在。而标准化处理法、归一化法及向量规范法的公式中包含指标所有样本信息的统计量,如平均值、总和及平方和等,所以稳定性较好;相反,极值处理法、线性比例法以及功效系数法等受个别极端数据如最大值、最小值、满意值、不容许值的影响较大,所以稳定性较差。郭亚军等提出了一种组合方法“极标复合法”,兼顾极值处理法和标准化处理法并进行了论证,指出在实际应用中,可遵循类似的思路设计构建多种复合方法以适应不同环境下的评价[8]。樊红艳、刘学录指出,原始数据无量纲化方法不同所得的排序结果也就明显不同,好的数据无量纲化方法应该保持原始数据整体的一致性和关联系数一致性,并且不以个别极值来进行数据的标准化方法等[9]。郭亚军、马凤妹、董庆兴则指出无量纲化方法影响被评价对象间的局部差异,因为拉开档次法的特点是能最大程度体现被评价对象之间的整体差异,建议选用使被评价对象间整体差异最大的无量纲化方法[10]。江文奇给出了6种无量纲化方法产生的属性值方差,同时在此基础上分析了不同无量纲化方法对属性权重影响的敏感性,属性值发生变化以及增加或减少方案情况下的方案保序性问题。结果表明,属性值的无量纲化方法不同,属性的客观权重也有所不同,不同的无量纲化方法对方案的敏感性和保序性也有差别。极差变化法与功效系数法得到的权重相同,方案保序性仅与d符号有关;标准化处理法可能造成Xi拉大或者减小差异,但属性权重均为1/m,且难以实现方案的保序性;线性比例法、向量规范化法和归一化法得到的方差与权重并不一定同向,难以实现方案的保序性[11]。
由此可见,不同的线性无量纲化方法在处理正向化指标数据时均有不同的适用条件,而且不同的无量纲化方法对指标权重及综合评价结果均产生重大影响[12-13]。因此,本文试图从与前人不同的视角对常用的8种线性无量纲化方法进行分析,找出不同线性无量纲化方法的某些共性和一般规律。
二、线性无量纲化方法特点分析
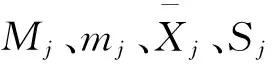
根据郭亚军等所给出的6种常用线性无量纲化方法[8],以及“极标复合法”和线性“奖优罚劣”方法,对其函数构成所使用的指标,原始数据中心点值和经变换后的中心点值、以及变换函数值域和其斜率和截距的表达式进行分析。八种线性无量纲化方法所涉及分析指标参照如下表1。

表1 八种线性无量纲化方法值域、中心点值、斜率及截距表达式表
根据表1各线性无量纲化方法的所用指标、值域、中心点值、斜率和截距的表达式,借鉴郭亚军所提出的六条理想性质,对上表各线性无量纲化方法的性质进行分析[8]。
1.单调性。由各方法斜率和截距的表达式可知,八种线性无量纲化方法均可表示为ξij=f(Xij)=kXij+b,i=1,2,…,m;j=1,2,…,n.的形式。由于所考虑的指标均先进行了正向化,即对于任意的一组原始指标数据,Xij越大则ξij越大。对于线性比例法也要求(Xij>0),由各变换函数表达式可知以上各种方法变换函数斜率k均大于0,且其变换函数对于某一组指标数据斜率不变。变换函数满足单调性,且对于正向化指标,变换函数单调递增。
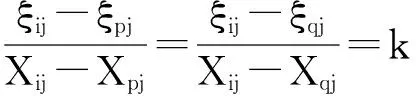
3.平移无关性与缩放无关性。对于平移无关性,左右平移f(Xij)=f(Xij+C3)(C3为任意常数)与缩放无关性f(Xij)=f(C4Xij)(C4为任意非零常数)的讨论。将Xij+C3代入方程ξij=f(Xij)=kXij+b(i=1,2,…,m;j=1,2,…,n),可得f(Xij+C3)=k1Xij+k1C3+b1,而平移无关性方程左边仍为f(Xij)=kXij+b。需要注意的是,由于原有数据的变化,线性方程斜率及截距的表达式中的数值可能也发生了变化,所以k1=k,b1=b不一定成立。经验证极标复合法和线性奖优罚劣方法也满足平移无关性,其他方法平移无关性结论均与文[8]相符。将C4Xij代入方程ξij=f(Xij)=kXij+b(i=1,2,…,m;j=1,2,…,n),可得f(C4Xij)=k2C4Xij+b2。极标复合法和线性奖优罚劣方法均满足缩放无关性,其他方法平移无关性结论均,这与郭亚军等研究相符。
4.稳定性。关于线性无量纲化方法稳定性问题,由于构成线性无量纲化方法的参照基准指标不同,变换函数也有差异,因此需要有统一的标准来限定变换函数的稳定性。一般认为,方差较小的变化方法稳定性较好。但方差主要考虑了数值与均值之间的关系。本文在考虑方差均值的基础上还分析了采用变换函数的中心点值(包括原始中心点值和变换函数中心点值)和值域来判断无量纲化方法的稳定性。
根据表1可知,标准化处理法和线性奖优罚劣方法都是以均值为原始中心点值,变换后中心点值为0。除此之外再加上极标复合法这一组合方法,其他方法是以中点值为原始中心点值,变换后的中心点值不确定。以中心点值为基准可以将上述各种方法分为三种类型。极标复合法为标准化法和极值化法的组合方法单独作为一类。具体分类如下表2。

表2 以中心点值为基准线性无量纲化方法分类表

从值域方面来考查稳定性。由于在某一指标数据区间内,值域的影响因素为斜率和截距。根据表1中线性无量纲化方法各变换函数方程有无截距,可将各线性无量纲化方法分为两类,见表3。

表3 无量纲化方法按截距是否为0进行分类表
由于线性比例法、归一化法和向量规范法均不满足平移无关性,且其截距为0,故其变换函数始终过原点,仅通过斜率来影响函数取值。而第一类方法则根据斜率和截距来影响变换函数取值。表4为不同值域的无量纲化方法分类
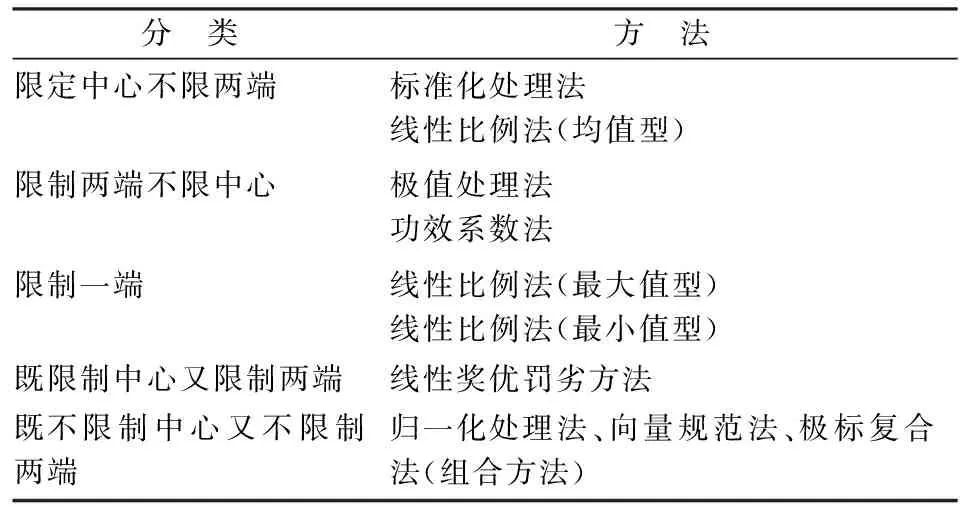
表4 不同值域的无量纲化方法分类表
由于变换函数的取值是随着X的不同而变化。由此既考虑函数的中心点值也考虑函数的值域最为理想,故相对于其他线性无量纲化方法,线性奖优罚劣方法较为理想。
极标复合法中心点值为均值和中点值的组合。它的优势是兼顾了均值和中心点值的特点。它不足为,由于标准化法值域不确定,而极值法值域始终为[0,1],因此在组合的情况下可能存在即便组合系数u非常小但标准化处理法所得取值范围仍将覆盖极值法取值的情行,从而使极值法的影响非常小,以至于可以忽略。同时,线性奖优罚劣方法也满足单调性、差异不变性、平移无关性、缩放无关性以及总量恒定性,且其值域为[-1,1],所以可将线性奖优罚劣方法和极值法进行组合更合适。需要注意的是,线性奖优罚劣方法其取值范围为[-1,1]而极差化处理法其取值范围为[0,1],为防止覆盖作用需对其中某一方法的取值范围进行平移放大,可得如下组合:


其中 λ∈[0,1]。这样既兼顾了两种方法的特点又考虑了取值范围不同的影响,该方法更加合理可靠。
各线性无量纲化方法斜率和截距的表达式可知,斜率的影响因素包括指标数据的标准差、极差、单个点值、指标值之和或指标值平方和等,其均与已正向化指标数据的取值区间中的某些数值有关;截距则由其基准值和斜率影响因素共同决定。由此,可根据斜率表达式、基准值和中心点值的关系,通过中点值替换均值或基准值等方法还可构造出如下正向化指标无量纲化方法,例如,设中点值为x0j=(Mj+mj)/2,则:

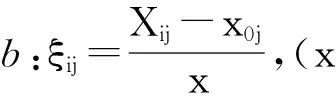
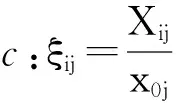
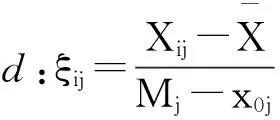
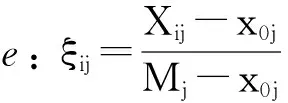

易知,方法a、b性质与标准法方法相同;方法c性质与线性比例法相同;方法d、e、f性质与线性奖优罚劣方法相同。但是以上方法的标准各不相同,取决于中心点值是均值还是中点值或是两者都考虑,同时取值区间也有所区别,理论上具有一定的可行性。
在对多指标数据进行线性无量纲化的过程中,现有文献均只考虑了使用同一种线性无量纲化方法对所有指标进行处理的情形,这显然是不合适的。其原因如下:第一,通过分析以上8种线性无量纲化方法的斜率和截距表达式可知,采用某一种线性无量纲化方法处理多种不同属性的指标数据,其均值、方差、最大值、最小值等指标数据也可能存在很大的差异,因此根据不同指标数据求得的变换函数的斜率大小可能完全不同,而且除截距为零的情况不受影响外,变换函数的截距也可能有较大的差异;第二,不同的线性无量纲化方法均有一定的适用范围,某一种无量纲化方法不可能同时适用于处理属性不同且差异很大的几组数据组成的样本。因此,将不同属性的指标数据根据其不同的数据特点选择不同的无量纲化方法进行处理成为可能。
对于同一个样本中几组不同属性的数据进行综合评价,使用多种线性无量纲化方法是否会引起总方差的变化,这种变化对于总体数据信息的流失是否会形成影响?其需要满足的限制条件是什么?还需要作进一步研究与分析。
三、多指标多种线性无量纲化方法案例分析
某集团公司考核其下属15个分公司的工作业绩,建立4项评价指标:X1表示人均实现利税额(万元/人),X2表示单位产值(万元/能耗),X3表示产品合格率(%),X4表示厂区绿化覆盖率(%)[12]。为便于本案例分析,所选指标均为正向化指标。各指标权重为:w1=0.35,w2=0.3,w3=0.2,w4=0.15。
原始数据无论采用何种无量纲化方法处理,其方差前后对比必然会发生变化。对于X1、X2这两个指标而言,其进行无量纲化前的方差一定比不论以何种方法进行无量纲化的方差要大很多,因为原始数据量级高于处理后的数据,故使用无量纲化方法后信息必然会流失。但是若将X1、X2原始数据缩小100倍处于[0,1]之间,则其方差小于分别进行极差无量纲化方法和线性奖优罚劣方法处理的方差,而极差化方法处理的方差比线性奖优罚劣方法处理的方差要小,故采用极差化方法处理更合适。同理,指标X3、X4采用线性奖优罚劣方法处理的方差小于极差无量纲化方法处理的方差,更接近于原始数据的方差。故指标X1、X2采用极差法指标X3、X4采用线性奖优罚劣方法。处理后的数据如下表6所示。

表5 各公司各指标原始数据表
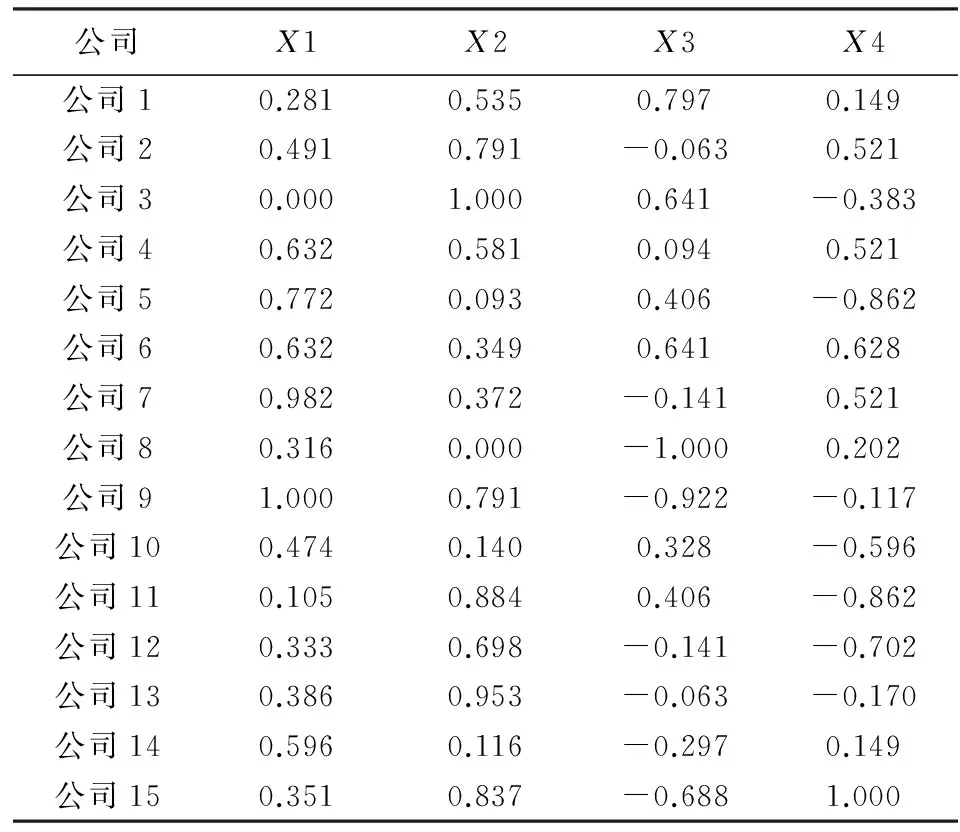
表6 经无量纲化后规范化数据表
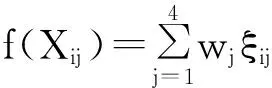

表6 各分公司业绩评价结果表
结果与张卫华等评价结果相差不大,但变换后方差更接近于原始数据的方差,信息保存更全,更加稳定,说明其方法可行。同时需要注意的是,经放大平移后的极差法可化为如下形式:
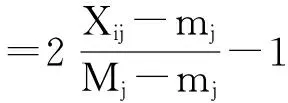
线性奖优罚劣方法为:

上面两种方法取值区间相同而基准不同,半极差和两端点到均值的最大值的倒数均为斜率,均体现了指标Xij的区间分布情况,当ξij=0时求得的Xij则为区间分布的中心点标准,极差法变换中心点始终为中点值,而线性奖优罚劣方法其中心点为均值。
四、结 论
本文通过对8种不同的线性无量纲化方法从函数的构成方面进行了详细的分析,论证了线性无量纲化方法满足单调性、差异比不变性、平移无关性与缩放无关性以及稳定性等特点,并根据线性无量纲化函数的分类特点,提出了多种线性无量纲化方法。根据不同指标属性的数据特点,在保证总体样本数据信息不流失的情况下,采用不同的无量纲化方法进行处理存在一定的可行性,并通过一个案例进行了实证分析,论证了其科学性和合理性。
[1] 郭亚军. 综合评价理论、方法及应用[M]. 北京:科学出版社, 2007.
[2] Gregory A J, Jackson M C. Evaluation Methodologies: A System of Use [J]. Journal of Operational Research, 1992,43(1).
[3] 易平涛, 张丹宁, 郭亚军, 等. 动态综合评价中的无量纲化方法[J]. 东北大学学报: 自然科学版, 2009, 30(6).
[4] Ma Fengmei, Guo Yajun. Density-induced Ordered Weighted Averaging Operators [J]. International Journal of Intelligent Systems, 2011(26).
[5] 朱孔来.评价指标的非线性无量纲模糊处理方法[J]. 统计与信息论坛,1997(3).
[6] 刘勇, Jeffrey Forrest, 刘思峰. 基于”奖优罚劣” 线性变换算子的区间数多目标灰色局势决策方法[J]. 统计与信息论坛, 2012, 27(4).
[7] 宋捷, 党耀国, 王正新. 基于强”奖优罚劣”算子的多指标灰靶决策模型. 系统工程与电子技术, 2010, 32(6).
[8] 郭亚军, 易平涛. 线性无量纲化方法的性质分析[J]. 统计研究, 2008, 25(2).
[9] 樊红艳, 刘学录. 基于综合评价法的各种无量纲化方法的比较和优选——以兰州市永登县的土地开发为例[J]. 湖南农业科学, 2010(17).
[10]郭亚军, 马凤妹, 董庆兴. 无量纲化方法对拉开档次法的影响分析[J]. 管理科学学报, 2011, 14(5).
[11]江文奇. 无量纲化方法对属性权重影响的敏感性和方案保序性[J]. 系统工程与电子技术, 2012, 34(12).
[12]张卫华, 赵铭军. 指标无量纲化方法对综合评价结果可靠性的影响及其实证分析[J]. 统计与信息论坛, 2005, 20(3).
[13]Chakraborty S. Yeh C H. A simulation comparison of normalization procedures for TOPSIS[C]. // International Conference on Computers and Industrial Engineering, 2009.
(责任编辑:张爱婷)
Character Analysis of Linear Dimensionless Methods
ZHAN Min1,2, LIAO Zhi-gao1, XU Jiu-ping2
(1. School of Management, Guangxi University of Science and Technology, Liuzhou 545006, China;2. Business School, Sichuan University,Chengdu 610064, China)
According to indexs used by the function form of the linear dimensionless method, the center value and range, and expression of the function to the slope and intercept, eight kinds of linear dimensionless methods commonly used were analyzed and we summarized the nature of the different linear dimensionless, and theoretical argumented. Meanwhile, through the classification and comparision of linear dimensionless method, this paper proposed the conceive that we can use various linear dimensionless methods in a multi-index comprehensive evaluation, and described the constructor of linear will also be possible and conducted empirical analysis.
slope; intercept; center value; range
2015-11-21;修复日期:2016-07-03
国家自然科学基金重点项目《大型水利水电工程建设项目集成管理理论与方法研究》(70831005);广西优秀中青年骨干教师培养工程资助项目(桂教人[2013]9号)
詹 敏,男,湖南长沙人,硕士生,研究方向:决策理论与方法; 廖志高,男,湖南隆回人,管理学博士,教授,研究方向:不确定决策理论与方法,物流与供应链; 徐玖平,男,重庆市人,理学博士,教授,研究方向:决策理论与方法。
C812∶O213.9
A
1007-3116(2016)12-0017-06

