无量纲化方法的选取原则

李玲玉，郭亚军，易平涛

（东北大学 工商管理学院，沈阳 110167）

在综合评价过程中，对评价数据的无量纲化处理是一项重要的基础性工作。到目前为止，研究与应用最多的是线性的无量纲化方法，且大部分是从多种无量纲化方法相互比较［1］的角度进行分析，试图寻找最优的无量纲化方法［2-8］。为进一步改进无量纲化方法的处理结果，文献［3，9］中在常用的线性无量纲化方法的基础上，分别提出了更为合理的极标复合法的复合无量纲化方法和改进的归一化法。而通过已有研究可知，每种无量纲化方法各有其特点。文献［5］中从无量纲化方法自身计算公式出发，分析了它们的特点及对综合评价值的影响，发现选用不同的无量纲化方法得出的评价结论往往不一致。文献［10］中对几种常用的线性无量纲化方法的稳定性进行分析，在此基础上，提出了一种新的无量纲化方法。而文献［11］中讨论了在综合评价模型及权重系数给定的情况下，综合评价结果（或排序）关于评价指标类型一致化、评价指标无量纲化方法的敏感性问题，首次指出综合评价值的大小不仅取决于权重系数，还取决于无量纲化方法的选择。

综上所述，无量纲化方法的选取直接决定了评价结果的可信性。本文在已有研究基础上，进一步构建了无量纲化方法的选取原则，并通过随机模拟仿真的方法，对各种原则进行了分析。然后，以拉开档次法为例，寻找最佳的无量纲化方法，期望能够最大程度体现被评价对象的差异以及提升该方法的稳定性。研究结果发现，线性比例法（分母取最小值mj）是最适合拉开档次法的无量纲化方法。

1 选取无量纲化方法的原则

1.1 选取无量纲化方法的3个原则

在选取无量纲化方法时，不单要考虑无量纲化方法的性质，还需将无量纲化方法同特定的综合评价方法结合来考虑，才能得出适合于该综合评价方法的最佳无量纲化方法。

文献［13］中对几种无量纲化方法的优劣进行了比较，发现多种无量纲化方法得出结论不一致的原因是有时忽略了线性无量纲化方法的变异信息不变性这一性质。若不具备变异信息不变性，则无量纲化处理前后的数据将具有不同的密集程度，必然影响综合评价结果。因此，下面给出无量纲化方法的变异性原则，该原则是为了尽可能地保留无量纲化处理前后数据之间的差异。

（1）变异性原则。选用无量纲化方法，应尽量保留指标数据所包含的变异信息（即指标数据无量纲化前后变异系数保持不变）［13］。

通常，综合评价的最终目标是拉开各被评价对象之间的差距。而使用不同的无量纲化方法进行预处理，综合评价结果的分散程度也会不同，因此，在满足原则（1）的前提下，给出差异性原则。

（2）差异性原则。选用无量纲化方法，应尽量体现被评价对象s1，s2，…，sn之间的差异，即选择使y1，y2，…，y n的离差平方和最大的无量纲化方法［12］。

理论上，给定一组评价数据，增加一个极端对象（指标值非常小或非常大），原有被评价对象之间的综合排序应具有一致性。对于权重与评价数据无关的评价方法（即主观赋权方法）这一结论完全成立，但是对于某些客观综合评价方法，如拉开档次法、离差最大化方法、均方差法等，评价结果受无量纲化方法和赋权方法的双重影响，该结论则不一定成立。本文将增加极端对象前后的综合排序的一致性程度称为评价方法的稳定性，评价方法固定，可以得到使评价方法稳定性最好的无量纲化方法，对应如下稳定性原则。

（3）稳定性原则。选取无量纲化方法，应使评价方法的稳定性最好，即极端对象对评价结果影响越小越好。

1.2 3个原则的分析思路

（1）变异性原则。无量纲化处理之后的数据应保留原始数据的变异信息。这里用变异系数来衡量指标数据的变异信息，其计算公式为

式中：σ为标准差；μ为均值。

该原则是从保证数据的结构特征出发，以尽量使参与评价的数据与原始数据具有相同的离散程度，在进行验证时比对无量纲化处理前后数据的变异系数。在选取无量纲化方法时，该原则为首要原则。除特殊目的须采用特定无量纲化方法外，凡是不满足变异性原则的无量纲化方法，可以不再进行其他原则的验证。

（2）差异性原则。无量纲化方法的选取，应使被评价对象的评价值y1，y2，…，y n的离差平方和最大，即

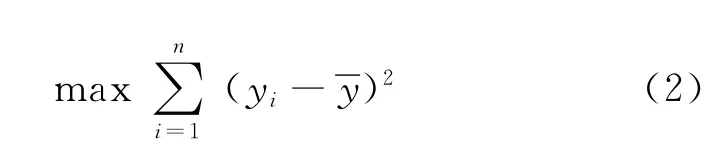
式中：y i为第i（i=1，2，…，n）个被评价对象的评价值；为评价值的平均值。

无量纲化方法的选取不能脱离评价方法本身，该差异性原则就是将无量纲化方法用于所选定的评价方法，以突出被评价对象之间的差异为目标，由于衡量差异性原则的公式同拉开档次法的目标函数相似，故对拉开档次法而言，该原则尽可能地突出了目标函数（式A4）的作用。不同点在于，目标函数（式A4）求出的是权重向量，而式（2）则是在用多种无量纲化方法对原始数据进行处理后，求出相应权重，再进行集结求得综合评价值以及评价值向量的离差平方和，最后选出离差平方和最大的评价值对应的无量纲化方法。

（3）稳定性原则。本文用Spearman相关系数来衡量增加极端对象前后原有被评价对象之间排序的相关性，相关系数越大，对应的无量纲化方法使得拉开档次法的评价结果越稳定。Spearman相关系数的计算公式［14］为

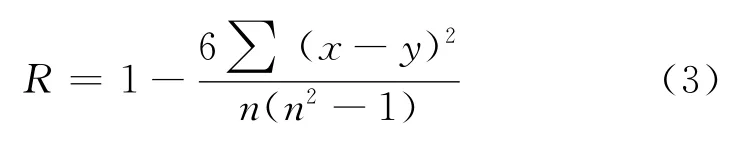
式中，（x-y）表示增加极端对象前后原有被评价对象排序值之差。

该原则从保证方法内部的结构特征出发，分析方法自身的稳定性。

2 仿真分析

选取7种常用的线性无量纲化方法：标准化处理法、极值处理法、向量规范化法、归一化处理法、线性比例法mj、线性比例法M j和线性比例法（均值）（线性比例法的计算公式为为特殊点，在本文分别取列最小值mj、列最大值M j和列均值），采用数值仿真方法，以拉开档次法为例（见附录）对选取无量纲化方法的原则进行分析。

2.1 变异性分析

根据原则（1），依据变异性原则设置如下数值仿真过程：

（1）设置仿真次数cnt；

（2）随机产生n行m列原始评价数据；

（3）分别用6种无量纲化方法进行数据预处理；

需要说明的是，标准化处理法处理之后的数据列均值为0，计算变异系数时结果无穷大，因此不对该方法进行仿真。

（4）计算每一种无量纲化方法处理后数据的变异系数；

（5）将处理后的数据与原始数据的变异系数进行比较，计算对应项差值的平方和。将仿真2 000次与10 000次的结果的标准差和均值进行比较，仿真结果如表1所示。

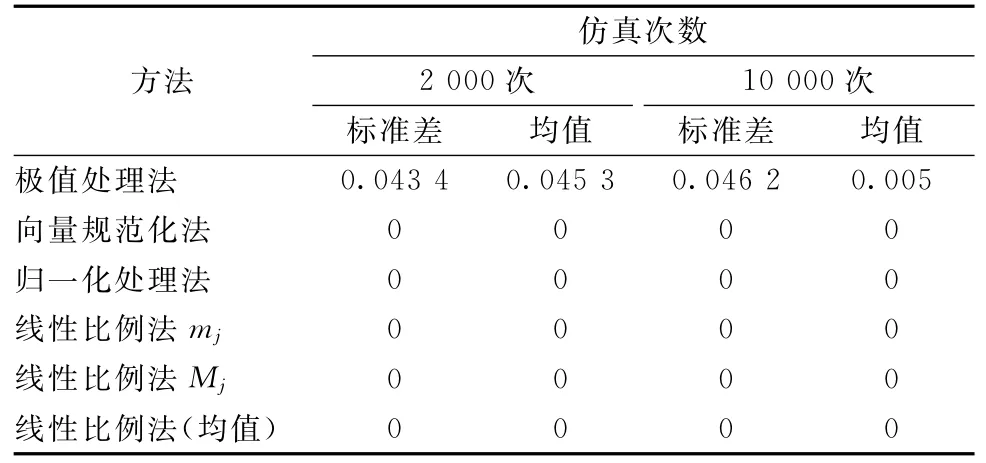
表1 各无量纲化方法变异信息仿真结果

由表1可见，用向量规范化法、归一化处理法和线性比例法（当x′分别取m j、M j和均值时）分别进行无量纲化处理后的数据变异系数，与原始数据变异系数对应项相减的平方和，经过多次仿真得到的结果无论是标准差还是均值都为0。说明向量规范化法、归一化处理法和线性比例法（当x′分别取m j、M j和均值时）均保留了原始数据的变异信息；而极值处理法没有保留原始变异信息。此外，不同仿真次数对仿真结果的影响不大，因此，将仿真次数均设定为2 000次。

2.2 差异性分析

根据原则（2），为了验证哪种无量纲化方法处理后综合评价值y1，y2，…，y n的离差平方和最大，使用Excel软件及其VBA 编程进行数值仿真，设置仿真步骤：

（1）设置仿真次数cnt；

（2）随机产生n×m矩阵A数据（假设都为极大型指标）；

（3）分别用7种线性无量纲化方法对矩阵A进行处理；

（4）采用拉开档次法对7种无量纲化处理后的信息矩阵进行求解；

（5）计算每种无量纲化得到的评价值的离差平方和，并按离差平方和由大到小进行排序，得到一组序值；

（6）循环cnt次，计算所有序值的平均值。

不同被评价对象个数与指标数目下均仿真2 000次，结果如表2所示。

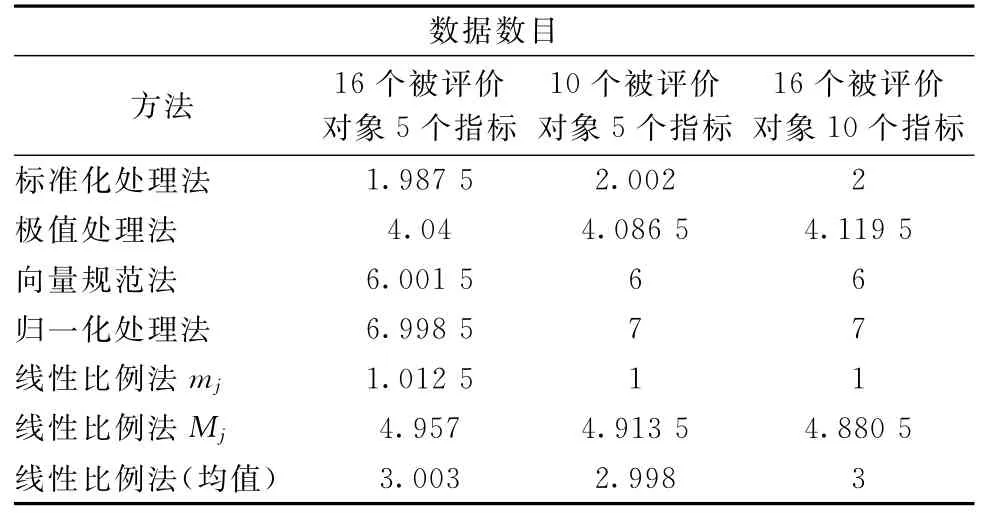
表2 各无量纲化方法对应的离差平方和排序值仿真结果

由表2仿真结果可见，在拉开档次法中使用线性比例法mj进行无量纲化处理得到的最大离差平方和基本上是7种无量纲化方法中最大的。尽管采用标准化处理法与线性比例法mj进行无量纲化后得到的综合评价值的离差平方和排序偶尔会变动，即标准化处理法得到的综合评价值的离差平方和偶尔会大于线性比例法mj的离差平方和，但总体趋势仍然是线性比例法mj能使被评价对象之间的整体差异最大。

分析表2数据可以发现，在用拉开档次法进行综合评价时，各种无量纲化方法处理后得到的综合评价值的离差平方和从大到小排序为：线性比例法mj＞标准化处理法＞线性比例法（均值）＞极值处理法＞线性比例法M j＞向量规范法＞归一化处理法。

2.3 稳定性分析

根据原则（3），分析各种无量纲化方法下拉开档次法的稳定性，设置仿真步骤：

（1）设置循环次数cnt；

（2）产生评价矩阵，随机指定n行m列的原始评价数据矩阵，即A=［x i j］n×m；

（3）分别用7种线性无量纲化方法对矩阵A进行处理；

（4）采用拉开档次法对7种无量纲化处理后的信息矩阵进行求解，计算各被评价对象的排序结果；

（5）增加一个被评价对象。按照

（极端对象各值距离各指标的最大值t个步长，步长为0.2σj，第1个极端对象由各指标的最大值组成）；或者按照

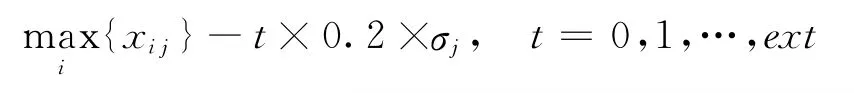
的方式增添单个被评价对象（设置极端对象各值距离各指标的最小值t个步长，步长为0.2σj，第1个极端对象由各指标的最小值组成），得到B=［x i+1，j］（n+1）×m；

（6）对数据矩阵B重复（3）～（4）；

（7）用Spearman's等级相关系数衡量原有被评价对象两次评价排序的相关性；

（8）仿真cnt次，计算并保存Spearman相关系数的平均值。

从最大值方向加入极端对象，仿真2 000次，各种无量纲化方法的仿真结果如图1所示。

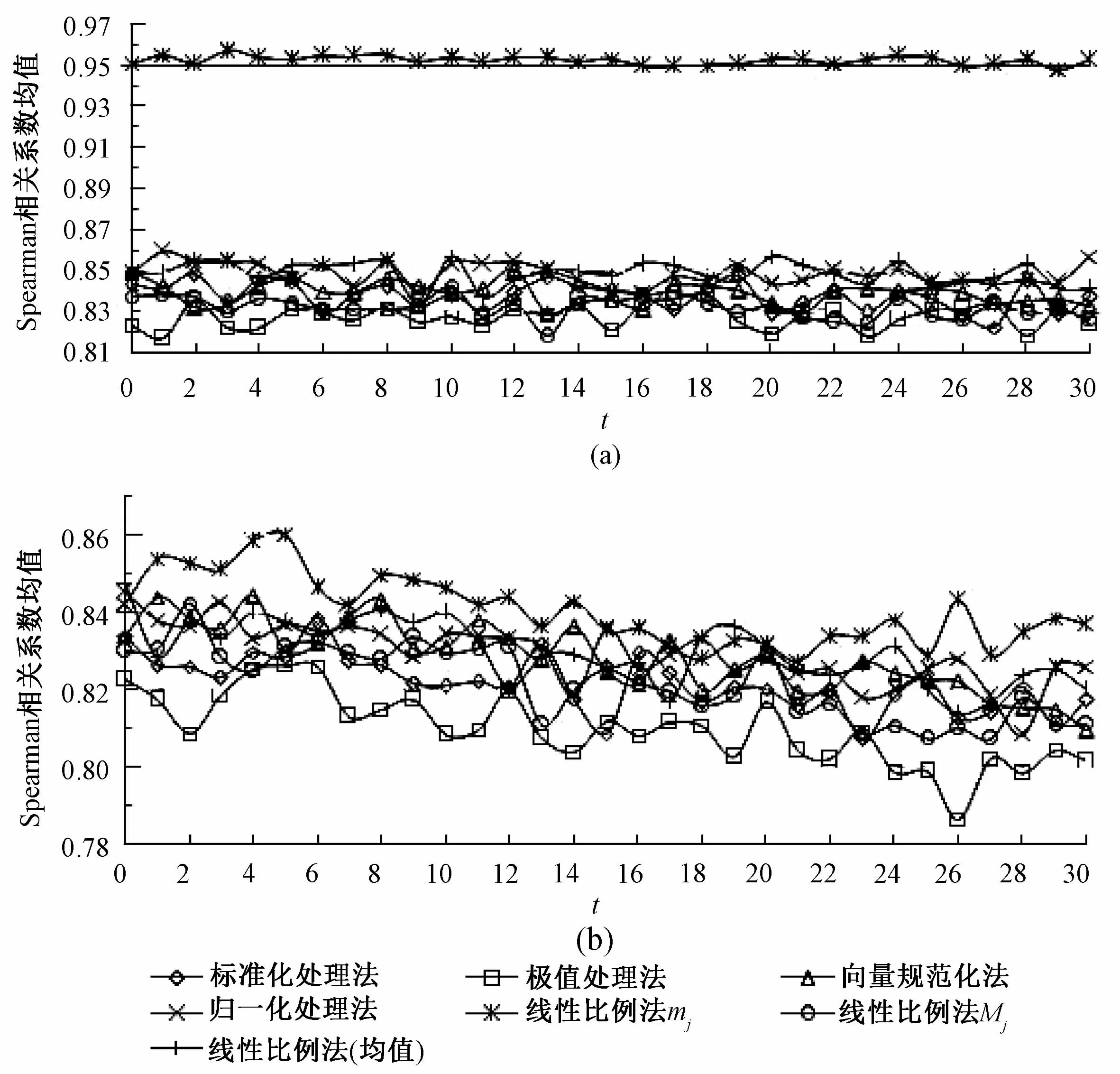
图1 从最大值方向增加极端对象时Spearman相关系数随步长t的变化

由图1可知：①无论评价数据服从均匀分布还是正态分布，线性比例法mj使得拉开档次法的稳定性最好；②评价数据服从均匀分布时，除线性比例法mj外，被评价对象的极端程度对结果的干扰程度不明显；③数据服从均匀分布时，线性比例法mj对拉开档次法的稳定性影响明显优于其他方法。

从最小值方向加入极端对象，仿真2 000次，各种无量纲化方法的仿真结果如图2所示。由图2可知：①无论评价数据服从均匀分布还是正态分布，线性比例法mj使得拉开档次法的稳定性最好；②随着极端对象到最小值的距离增大，方法的稳定性有下降的趋势。

由以上仿真结果可知，无论评价数据服从均匀分布还是正态分布，都可以得到线性比例法m j，使得拉开档次法的稳定性最好的结论。

3 结论

在3个原则下进行了相应的仿真，分别得出以下结论：

（1）针对原则（1），通过仿真可知，向量规范化法、归一化处理法和3 种线性比例法（分别为m j、M j和）保留了原始数据变异信息。

图2 从最小值方向增加极端对象时Spearman秩相关系数随步长t的变化

（2）针对原则（2），在拉开档次法中应用7种无量纲化方法，得到的综合评价值的离差平方和按从大到小排序为：线性比例法mj＞标准化处理法＞线性比例法（均值）＞极值处理法＞线性比例法M j＞向量规范法＞归一化处理法。

采用各种无量纲化方法分别对原始数据进行预处理时，因为它们的计算公式不同，得到的无量纲的数据标准差也会不同。处理后的数据标准差越大，综合评价结果的离差平方和也越大。

（3）针对原则（3），在拉开档次法中应用7种无量纲化方法，采用线性比例法mj能够极大地提升拉开档次法的稳定性，这是无量纲化方法与拉开档次法求权重的交互影响得到的结果。

综合上述3条结论，得出适合于拉开档次法的最佳无量纲化方法为线性比例法mj。

4 结语

本文构建了选取无量纲化方法的3个原则，然后以拉开档次法为例，对3个原则进行了仿真分析。最后，得出线性比例法mj（mj≠0）是适合于拉开档次法的最佳无量纲化方法的结论。本文的研究思路可为其他综合评价方法选取无量纲化方法的研究提供参考，以解决评价者面对众多无量纲化方法无从选择的难题。

附录

拉开档次法简介

拉开档次法［12］是从整体上尽可能体现各被评价对象之间差异的综合评价方法，其原理如下：

设x1，x2，…，xm为极大型指标（即指标取值越大越好），取其线性函数为被评价对象的综合评价函数，即

式中：w=（w1，w2，…，w m）T是m维待定正向量（其作用相当于权系数向量）；x=（x1，x2，…，x m）T为被评价对象的指标向量。如将第i个被评价对象Oi的m个无量纲化后的观测值x i1，xi2，…，xim代入式（1），即得

则式（2）可写为y=Aw。

确定权重系数向量w的准则是求指标向量X的线性函数wTX，使此函数对n个被评价对象取值的分散程度或方差尽可能大。

而变量y=wTx按n个被评价对象取值构成样本的方差为

显然，对w不加限制时，式（3）可取任意大的值。这里限定wTw=1，求式（3）的最大值，即选择w，使得