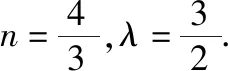阿波罗尼斯圆及其应用

江西 孙春生

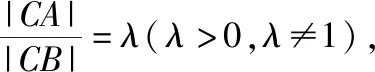
1.在以A,B为定点的阿氏圆上任意一点，到A,B两点的距离之比都等于定值λ(λ≠1)；

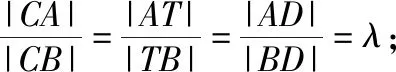
3.顶点C的轨迹就是阿氏圆，是以TD为直径的圆，且A,B,T,D四点共线.

阿波罗尼斯圆常以以下三种形式出现：①作为数学文化试题直接应用；②需要挖掘隐含条件，转化使用；③与立体几何知识联系在一起，拓展应用．以下分类例析．

一、作为数学文化题呈现

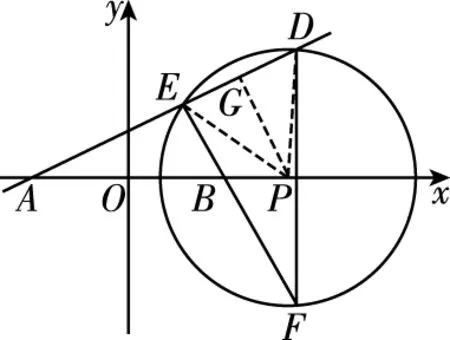
【例1】阿波罗尼斯(古希腊数学家，约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果，他证明过这样一个命题：平面内与两个定点距离的比为常数k(k>0,k≠1)的点的轨迹是圆，后人把这个圆称为阿波罗尼斯圆．已知定点A(-2,0),B(2,0)，动点C满足|AC|=2|BC|，则动点C的轨迹为一个阿波罗尼斯圆，记此圆为圆P，已知点D在圆P上(点D在第一象限)，AD交圆P于点E，连接EB并延长交圆P于点F，连接DF，当∠DFE=30°时，直线AD的斜率为

( )

【分析】先设点C(x,y)，根据|AC|=2|BC|求出点C的轨迹方程，过圆心P作PG⊥DE于点G，求出|PG|，|PA|，可求出sin∠PAG的值，再利用同角三角函数的基本关系可求得直线AD的斜率.

因为∠DPE=2∠DFE=60°，|PE|=|PD|，则△DPE为等边三角形，

【评注】近几年高考数学文化题难度加大，首先要明白题中含义，明确数学关系，再结合相关数学知识来解决问题.

二、构造阿波罗尼斯圆

( )

解法一:设点C(m,n)，

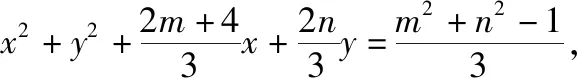
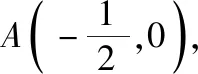
【评注】本题解题的关键是构造2|MA|=|MC|，得到M所在圆就是对应的阿波尼罗斯圆，然后逆向求出定点C的坐标，利用三角形两边之差小于第三边的方法解决.本题的解法二，直接利用阿波罗尼斯圆中，角平分线的性质来解，简洁明了.

三、挖掘隐含条件使用

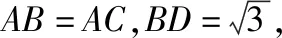
【分析】此类题我们通常想到的是用解斜三角形的方法，但如果利用AB=2AD，构造阿波罗尼斯圆来解决，则能优化思维，简化运算．

解法一:用解斜三角形的方法，设AD=CD=m，

则AB=2m，根据面积公式得,

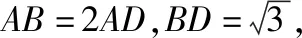
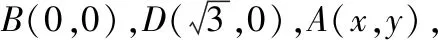
所以(S△ABCmax)=BD·r=2.

【评注】解题过程中，若多关注问题的形成，注重知识的积累，形成解法的多样性，在答题时往往能更胜一筹．

四、在空间中拓展应用

【例4】在棱长为2的正方体ABCD-A1B1C1D1中，点P是正方体的表面ADD1A1(包括边界)上的动点，若动点P满足PA=2PD，则点P所形成的圆的半径为；若E是CD的中点，且正方体的表面ADD1A1(包括边界)上的动点F满足条件∠AFB=∠EFD，则三棱锥F-ACD体积的最大值是．

解:如图，以D为坐标原点，DA为x轴，DD1为y轴，建立如图所示的平面直角坐标系，则A(2,0),D(0,0)，

设P(x，y)，

因为AB⊥平面ADD1A1，CD⊥平面ADD1A1，

所以∠FAB=90°，∠FDE=90°，

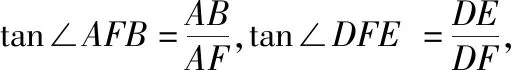
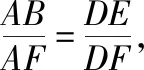
因为E是CD的中点，所以AF=2DF，由此得到点F的轨迹即为P点的轨迹.

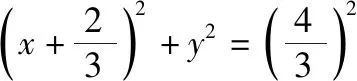
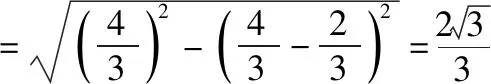
则三棱锥P-ACD体积的最大值是

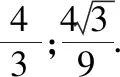
【评注】第二问中要根据角度相等，充分利用空间位置关系，得出AF=2DF这一几何条件，再利用阿波罗尼斯圆的性质解决问题．

五、 逆向构造探究题

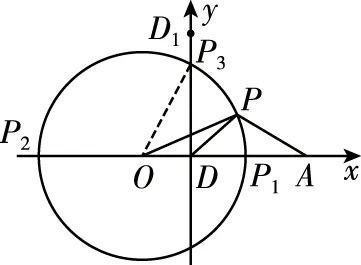
【例5】已知圆C：(x-3)2+y2=4，直线l：(m+1)x-(3m-1)y+m-3=0．

(1)求直线l所过定点A的坐标及当直线l被圆C所截得的弦长最短时m的值；

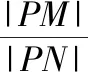
解法一：(1)定点A(2,1)，m=1，过程略．

假设存在定点N(3,t)满足题意，则有|PM|2=λ2|PN|2，

整理得(x-3)2+(y-3)2=λ2[(x-3)2+(y-t)2]，

又因为(x-3)2=4-y2，

所以4-y2+(y-3)2=λ2[4-y2+(y-t)2]，

化简得(2λ2t-6)y-(λ2t2+4λ2-13)=0,

当λ=1，t=3时，点N与点M重合，不符合题意，

解法二:设过定点M,N的阿波罗尼斯圆交直线x=3于T,D两点，则T(3,2),D(3,-2)分别为△MAC的内角平分线与外角平分线与直线MN的交点，M(3,3)，设N(3,n)，将点的坐标代入